19.1多边形内角和(第1课时) 教案 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.1多边形内角和(第1课时) 教案 沪科版初中数学八年级(下) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览

文档简介
第19章 四边形
19.1 多边形内角和
第1课时 多边形的内角和
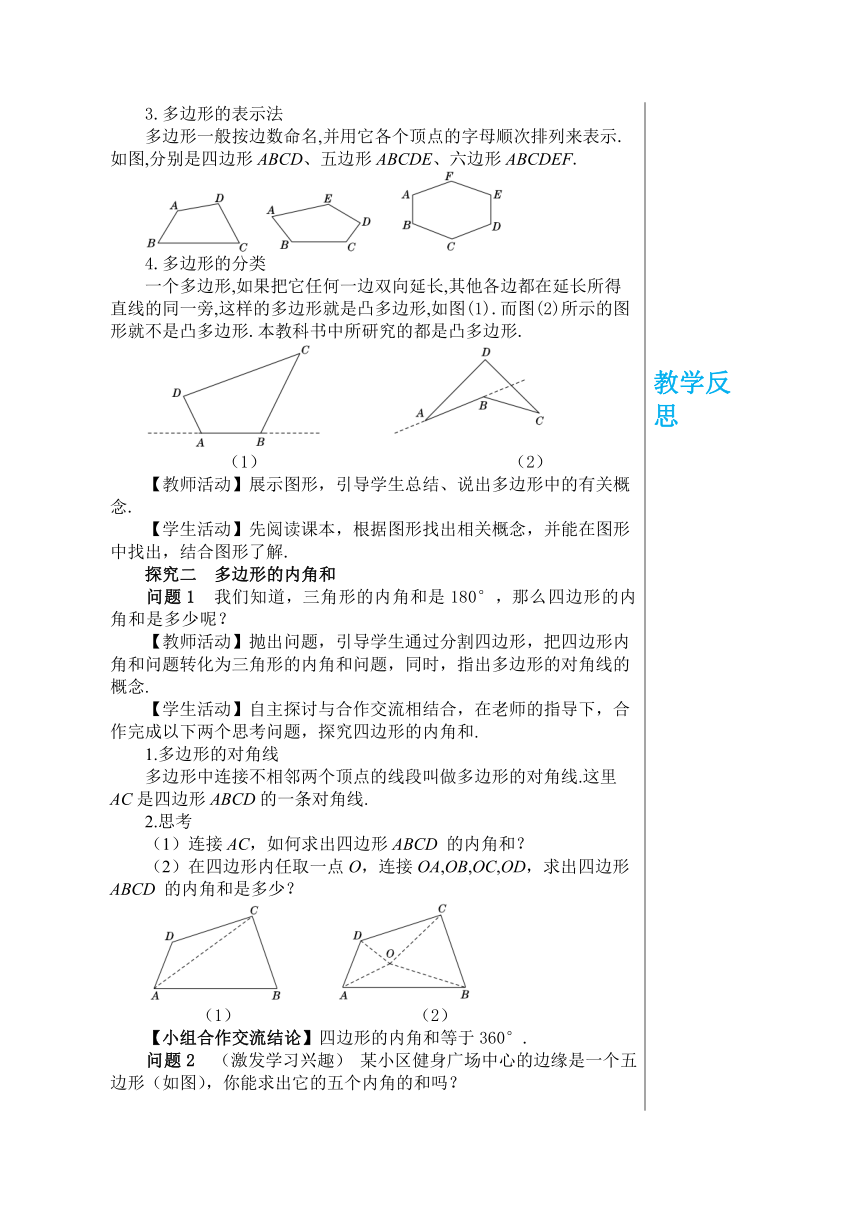
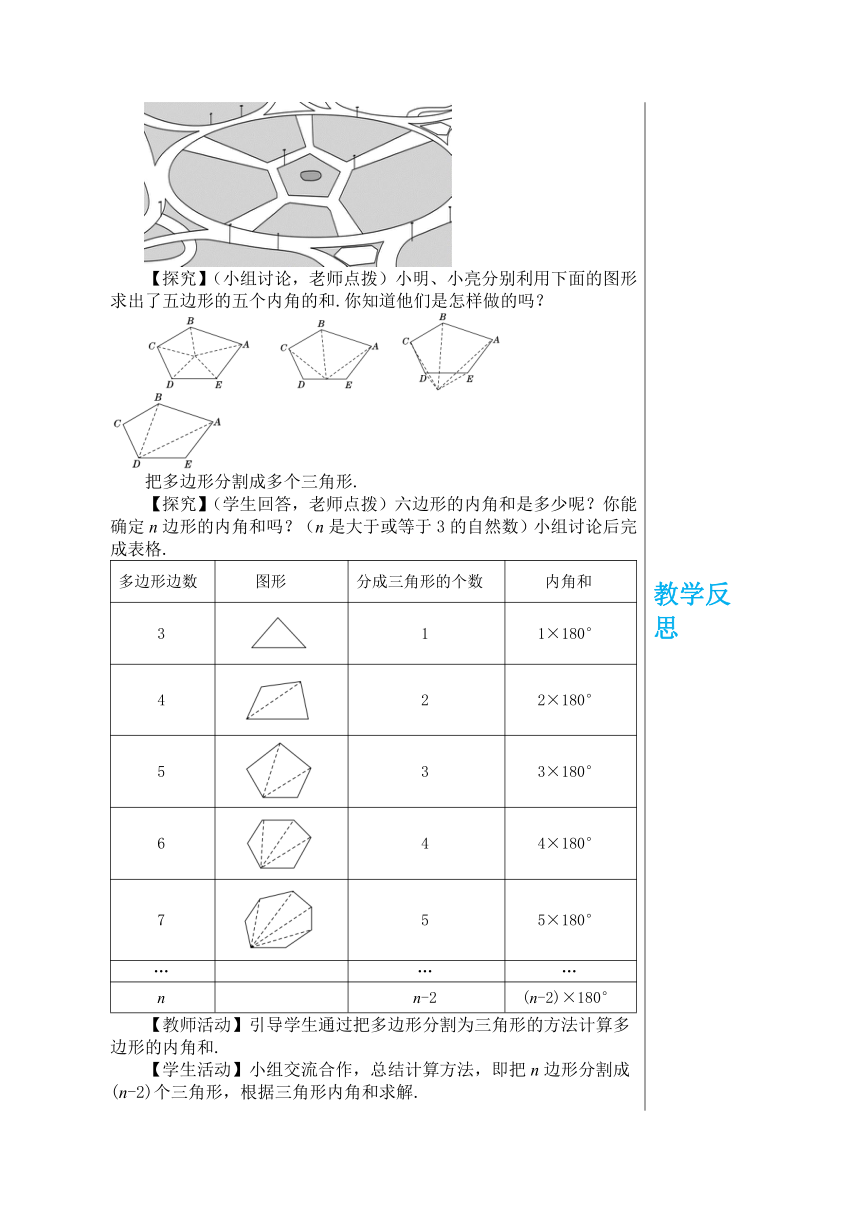
教学目标 1.了解多边形、正多边形及多边形的边、顶点、内角、外角、对角线等概念. 2.会用顶点字母表示多边形. 2.能够应用多边形的内角和定理解决有关的问题. 3.经历多边形的内角和定理的探究过程,进一步体会转化的数学思想. 教学重难点 重点:多边形内角和定理. 难点:多边形的内角和定理的探索. 教学过程 知识回顾 问题 (学生自主完成,老师引导) 1.在△ABC中,∠A=50°,∠B=30°,则∠C=_____. 2.正方形的内角和等于多少度?长方形呢? 3.如图,对于任意形状的四边形,它的内角和是多少度呢?你是怎么得到的? 探究新知 探究一 多边形的有关概念及表示法 1.多边形的定义 在平面内,有若干条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形. 2.有关概念 边:组成多边形的线段叫做多边形的边. 顶点:相邻两边的公共端点叫做多边形的顶点. 内角:多边形中相邻两边组成的角叫做多边形的内角,简称多边形的角. 外角:在顶点处一边与另一边的延长线所组成的角叫做多边形的外角. 3.多边形的表示法 多边形一般按边数命名,并用它各个顶点的字母顺次排列来表示.如图,分别是四边形ABCD、五边形ABCDE、六边形ABCDEF. 4.多边形的分类 一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形就是凸多边形,如图(1).而图(2)所示的图形就不是凸多边形.本教科书中所研究的都是凸多边形. (1) (2) 【教师活动】展示图形,引导学生总结、说出多边形中的有关概念. 【学生活动】先阅读课本,根据图形找出相关概念,并能在图形中找出,结合图形了解. 探究二 多边形的内角和 问题1 我们知道,三角形的内角和是180°,那么四边形的内角和是多少呢? 【教师活动】抛出问题,引导学生通过分割四边形,把四边形内角和问题转化为三角形的内角和问题,同时,指出多边形的对角线的概念. 【学生活动】自主探讨与合作交流相结合,在老师的指导下,合作完成以下两个思考问题,探究四边形的内角和. 1.多边形的对角线 多边形中连接不相邻两个顶点的线段叫做多边形的对角线.这里AC是四边形ABCD的一条对角线. 2.思考 (1)连接AC,如何求出四边形ABCD 的内角和? (2)在四边形内任取一点O,连接OA,OB,OC,OD,求出四边形ABCD 的内角和是多少? (1) (2) 【小组合作交流结论】四边形的内角和等于360°. 问题2 (激发学习兴趣) 某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗? 【探究】(小组讨论,老师点拨)小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗? 把多边形分割成多个三角形. 【探究】(学生回答,老师点拨)六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格. 多边形边数图形分成三角形的个数内角和311×180°422×180°533×180°644×180°755×180°………nn-2(n-2)×180°
【教师活动】引导学生通过把多边形分割为三角形的方法计算多边形的内角和. 【学生活动】小组交流合作,总结计算方法,即把n边形分割成(n-2)个三角形,根据三角形内角和求解. 【总结】(学生总结,老师点评) 多边形的内角和定理:n边形的内角和等于(n-2)·180°. 【例1】(小组讨论,老师指导)如图,在四边形ABCD中,∠A+∠C=180,∠B与∠D有怎样的关系? 【解】∵ 在四边形ABCD中,∠A+∠C=180,∠A+∠B+∠C+∠D=360, ∴ ∠B+∠D=180. 【师生交流结论】如果四边形的一组对角互补,那么另一组对角也互补. 【例2】(合作探究,解决问题)一个多边形的内角和为1 440,则它是几边形? 【解】设这个多边形是n边形,则180·(n-2)=1 440, ∴ n=10, ∴ 这个多边形是十边形. 【总结】已知多边形内角和求边数时,一般是设出多边形的边数,根据多边形内角和公式列方程求解. 跟踪训练(学生独立完成) 1.六边形的内角和为( ) A.1 260° B.1 080° C.900° D.720° 2.下列角度中能成为某多边形的内角和的是( ) A.270° B.560° C.1 800° D.1 900° 3.八边形的七个内角都为150,则第八个内角=________. 4.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少? 答案:1.D 2.C 3.30° 4.七边形 900° 探究三(小组讨论) 正多边形的内角 1.正三角形(等边三角形)的每个内角等于多少度?你是怎么计算的? 2.正四边形(正方形)的每个内角等于多少度?你是怎么计算的? 3.正五边形、正六边形、正八边形呢?…正n边形呢? 【教师活动】引导学生求出正多边形的内角和,根据正多边形的内角相等,求出每一个内角的度数. 【学生活动】先独立完成计算,再在小组内交流答案,总结计算公式. 【师生总结】正n边形的每个内角度数为. 跟踪训练 1.正八边形的每个内角都是( ) A.60° B.80° C.100° D.135° 2.一个多边形的每个内角均为120,则这个多边形是( ) A.正四边形 B.正五边形 C.正六边形 D.正七边形 答案:1.D 2.C 【拓展】(学生动手实践)截去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流. 不过顶点 五边形 过一顶点 四边形 过两顶点 三角形 答案:540° 360° 180° 【总结】截一个多边形的一个角时,一定注意截法,注意分类讨论. 课堂练习 1.一个多边形的内角和为540°,则它是( ) A.四边形 B.五边形 C.六边形 D.七边形 2.一个多边形的内角和为1 800°, 截去一个角后, 得到的多边形的内角和 为( ) A.1 620° B.1 800° C.1 980° D.以上答案都有可能 3.多边形每一个内角都等于150°,则该多边形的边数是( ) A.10 B.11 C.12 D.13 4.m边形与n边形内角和的差为720°,则m与n的差为( ) A.2 B.3 C.4 D.5 5.小彬求出一个正多边形的一个内角为145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由. 6.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在模板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,判断此模板是否合格?为什么? 参考答案 1.B 2.D 3.C 4.C 5. 解:不正确,理由如下: 设多边形是n边形,由题意得 145×n=(n-2)×180. 解得n≈10.3. 又n是正整数,n=10.3不符合题意, ∴ 他求的正多边形内角的度数不正确. 6.解:不合格,组成的五边形的内角和不是540°. 课堂小结 1.多边形的内角和定理:n边形的内角和等于(n - 2)·180°. 2.正n边形的每个内角度数为. 布置作业 教材第74页习题19.1第1题. 板书设计 第1课时 多边形的内角和 多边形的内角和定理:n边形的内角和等于(n-2)·180°. 例1 如图,在四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系? 例2 一个多边形的内角和为1 440°,则它是几边形? 教学反思 教学反思 教学反思 教学反思 教学反思
19.1 多边形内角和
第1课时 多边形的内角和
教学目标 1.了解多边形、正多边形及多边形的边、顶点、内角、外角、对角线等概念. 2.会用顶点字母表示多边形. 2.能够应用多边形的内角和定理解决有关的问题. 3.经历多边形的内角和定理的探究过程,进一步体会转化的数学思想. 教学重难点 重点:多边形内角和定理. 难点:多边形的内角和定理的探索. 教学过程 知识回顾 问题 (学生自主完成,老师引导) 1.在△ABC中,∠A=50°,∠B=30°,则∠C=_____. 2.正方形的内角和等于多少度?长方形呢? 3.如图,对于任意形状的四边形,它的内角和是多少度呢?你是怎么得到的? 探究新知 探究一 多边形的有关概念及表示法 1.多边形的定义 在平面内,有若干条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形. 2.有关概念 边:组成多边形的线段叫做多边形的边. 顶点:相邻两边的公共端点叫做多边形的顶点. 内角:多边形中相邻两边组成的角叫做多边形的内角,简称多边形的角. 外角:在顶点处一边与另一边的延长线所组成的角叫做多边形的外角. 3.多边形的表示法 多边形一般按边数命名,并用它各个顶点的字母顺次排列来表示.如图,分别是四边形ABCD、五边形ABCDE、六边形ABCDEF. 4.多边形的分类 一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形就是凸多边形,如图(1).而图(2)所示的图形就不是凸多边形.本教科书中所研究的都是凸多边形. (1) (2) 【教师活动】展示图形,引导学生总结、说出多边形中的有关概念. 【学生活动】先阅读课本,根据图形找出相关概念,并能在图形中找出,结合图形了解. 探究二 多边形的内角和 问题1 我们知道,三角形的内角和是180°,那么四边形的内角和是多少呢? 【教师活动】抛出问题,引导学生通过分割四边形,把四边形内角和问题转化为三角形的内角和问题,同时,指出多边形的对角线的概念. 【学生活动】自主探讨与合作交流相结合,在老师的指导下,合作完成以下两个思考问题,探究四边形的内角和. 1.多边形的对角线 多边形中连接不相邻两个顶点的线段叫做多边形的对角线.这里AC是四边形ABCD的一条对角线. 2.思考 (1)连接AC,如何求出四边形ABCD 的内角和? (2)在四边形内任取一点O,连接OA,OB,OC,OD,求出四边形ABCD 的内角和是多少? (1) (2) 【小组合作交流结论】四边形的内角和等于360°. 问题2 (激发学习兴趣) 某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗? 【探究】(小组讨论,老师点拨)小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗? 把多边形分割成多个三角形. 【探究】(学生回答,老师点拨)六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格. 多边形边数图形分成三角形的个数内角和311×180°422×180°533×180°644×180°755×180°………nn-2(n-2)×180°
【教师活动】引导学生通过把多边形分割为三角形的方法计算多边形的内角和. 【学生活动】小组交流合作,总结计算方法,即把n边形分割成(n-2)个三角形,根据三角形内角和求解. 【总结】(学生总结,老师点评) 多边形的内角和定理:n边形的内角和等于(n-2)·180°. 【例1】(小组讨论,老师指导)如图,在四边形ABCD中,∠A+∠C=180,∠B与∠D有怎样的关系? 【解】∵ 在四边形ABCD中,∠A+∠C=180,∠A+∠B+∠C+∠D=360, ∴ ∠B+∠D=180. 【师生交流结论】如果四边形的一组对角互补,那么另一组对角也互补. 【例2】(合作探究,解决问题)一个多边形的内角和为1 440,则它是几边形? 【解】设这个多边形是n边形,则180·(n-2)=1 440, ∴ n=10, ∴ 这个多边形是十边形. 【总结】已知多边形内角和求边数时,一般是设出多边形的边数,根据多边形内角和公式列方程求解. 跟踪训练(学生独立完成) 1.六边形的内角和为( ) A.1 260° B.1 080° C.900° D.720° 2.下列角度中能成为某多边形的内角和的是( ) A.270° B.560° C.1 800° D.1 900° 3.八边形的七个内角都为150,则第八个内角=________. 4.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少? 答案:1.D 2.C 3.30° 4.七边形 900° 探究三(小组讨论) 正多边形的内角 1.正三角形(等边三角形)的每个内角等于多少度?你是怎么计算的? 2.正四边形(正方形)的每个内角等于多少度?你是怎么计算的? 3.正五边形、正六边形、正八边形呢?…正n边形呢? 【教师活动】引导学生求出正多边形的内角和,根据正多边形的内角相等,求出每一个内角的度数. 【学生活动】先独立完成计算,再在小组内交流答案,总结计算公式. 【师生总结】正n边形的每个内角度数为. 跟踪训练 1.正八边形的每个内角都是( ) A.60° B.80° C.100° D.135° 2.一个多边形的每个内角均为120,则这个多边形是( ) A.正四边形 B.正五边形 C.正六边形 D.正七边形 答案:1.D 2.C 【拓展】(学生动手实践)截去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流. 不过顶点 五边形 过一顶点 四边形 过两顶点 三角形 答案:540° 360° 180° 【总结】截一个多边形的一个角时,一定注意截法,注意分类讨论. 课堂练习 1.一个多边形的内角和为540°,则它是( ) A.四边形 B.五边形 C.六边形 D.七边形 2.一个多边形的内角和为1 800°, 截去一个角后, 得到的多边形的内角和 为( ) A.1 620° B.1 800° C.1 980° D.以上答案都有可能 3.多边形每一个内角都等于150°,则该多边形的边数是( ) A.10 B.11 C.12 D.13 4.m边形与n边形内角和的差为720°,则m与n的差为( ) A.2 B.3 C.4 D.5 5.小彬求出一个正多边形的一个内角为145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由. 6.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在模板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,判断此模板是否合格?为什么? 参考答案 1.B 2.D 3.C 4.C 5. 解:不正确,理由如下: 设多边形是n边形,由题意得 145×n=(n-2)×180. 解得n≈10.3. 又n是正整数,n=10.3不符合题意, ∴ 他求的正多边形内角的度数不正确. 6.解:不合格,组成的五边形的内角和不是540°. 课堂小结 1.多边形的内角和定理:n边形的内角和等于(n - 2)·180°. 2.正n边形的每个内角度数为. 布置作业 教材第74页习题19.1第1题. 板书设计 第1课时 多边形的内角和 多边形的内角和定理:n边形的内角和等于(n-2)·180°. 例1 如图,在四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系? 例2 一个多边形的内角和为1 440°,则它是几边形? 教学反思 教学反思 教学反思 教学反思 教学反思
