19.2平行四边形(第1课时) 教案 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.2平行四边形(第1课时) 教案 沪科版初中数学八年级(下) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览

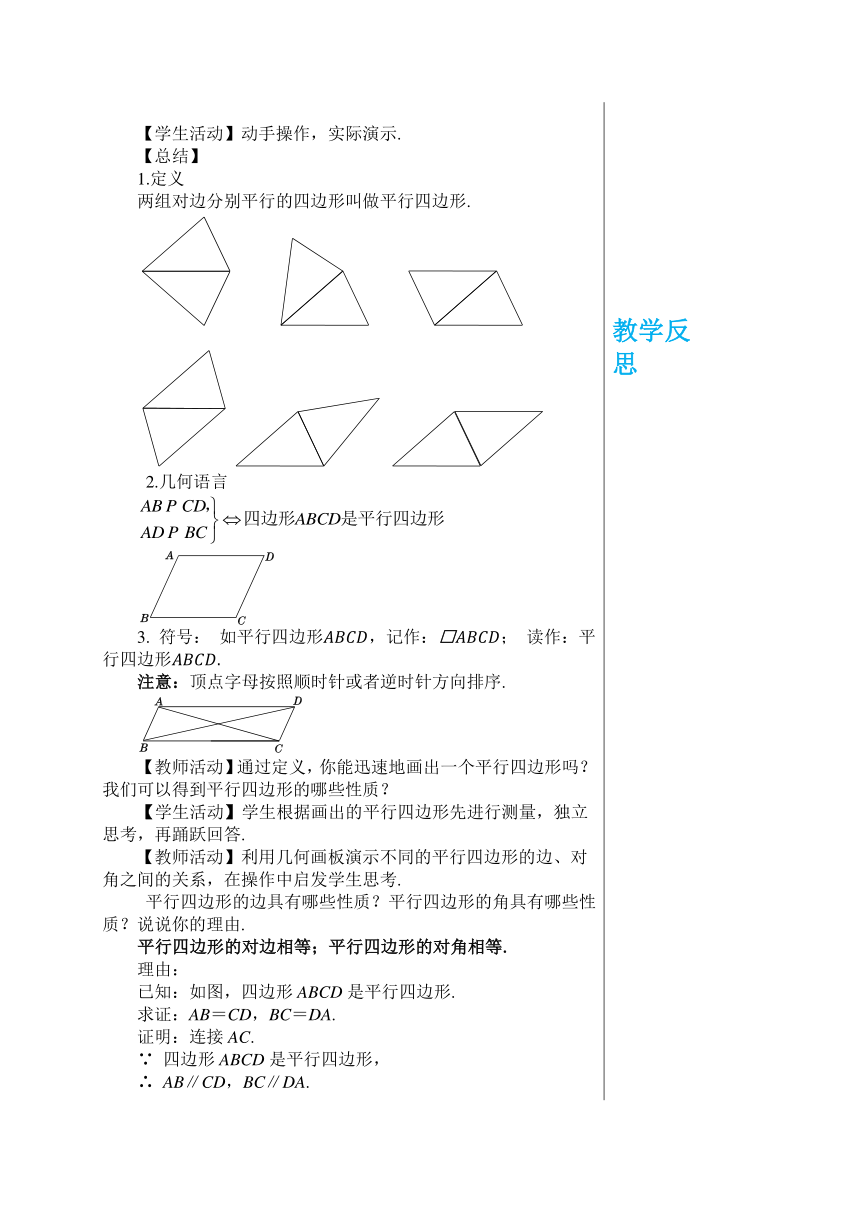

文档简介
第19章 四边形
19.2 平行四边形
第1课时 平行四边形边、角的性质
教学目标 1.引导学生理解平行四边形的定义,掌握平行四边形对边相等、对角相等的性质,并能够证明. 2.经历平行四边形性质的探究、归纳过程,让学生体会通过观察、猜想、操作、论证获得数学知识的方法. 教学重难点 重点:平行四边形的性质. 难点:证明平行四边形的性质. 教学过程 复习巩固 观察图形,说出下列图形边的位置有什么特征? 两组对边分别平行的四边形叫做平行四边形. 导入新课 观察这些图片,它们是否都有平行四边形的形象. 探究新知 拼一拼 取两个全等的三角形纸片,将它们相等的一边重合,得到一个四边形. 【学生活动】动手操作,实际演示. 【总结】 1.定义 两组对边分别平行的四边形叫做平行四边形. 2.几何语言 3. 符号: 如平行四边形,记作:□; 读作:平行四边形 注意:顶点字母按照顺时针或者逆时针方向排序. 【教师活动】通过定义,你能迅速地画出一个平行四边形吗?我们可以得到平行四边形的哪些性质? 【学生活动】学生根据画出的平行四边形先进行测量,独立思考,再踊跃回答. 【教师活动】利用几何画板演示不同的平行四边形的边、对角之间的关系,在操作中启发学生思考. 平行四边形的边具有哪些性质?平行四边形的角具有哪些性质?说说你的理由. 平行四边形的对边相等;平行四边形的对角相等. 理由: 已知:如图,四边形ABCD是平行四边形. 求证:AB=CD,BC=DA. 证明:连接AC. ∵ 四边形ABCD是平行四边形, ∴ AB∥CD,BC∥DA. ∴ ∠1=∠2,∠3=∠4. 在△ABC和△CDA中, ∵∠1=∠2,AC=CA,∠3=∠4, ∴ △ABC≌△CDA(ASA). ∴ AB=CD,BC=DA. ∠DAB=∠DCB,∠B=∠D. 【教师引导】利用问题的形式引导学生,我们证明线段或者角相等的方法有哪些?图中没有三角形怎么办?全等三角形的判定有哪些? 【学生活动】根据老师的引导,整理整体思路,先小组合作交流,写出已知和求证,其中两名学生在黑板上板演解题过程. 【板书总结】师生共同总结平行四边形的边、角性质. 平行四边形的对边平行. 几何语言:∵ 四边形ABCD是平行四边形, ∴ AB∥CD,BC∥AD. 性质定理1:平行四边形的对边相等. 几何语言:∵ 四边形ABCD是平行四边形, ∴ AB=CD,BC=AD. 性质定理2:平行四边形的对角相等. 几何语言:∵ 四边形ABCD是平行四边形, ∴ ∠A=∠C,∠B=∠D. 【例1】已知:如图,□ABCD中,BE平分∠ABC交AD于点E. (1)如果AE=2,求CD的长; (2)如果∠AEB=40°,求∠C的度数. 【解】 (1)∵ BE平分∠ABC,且AD∥BC, ∴ ∠ABE=∠EBC=∠AEB. ∴ AB=AE=2. 又∵ CD=AB, ∴ CD=2. (2)由(1)知 ∠AEB =∠ABE=40°, ∴ ∠A=180°-(40°+40°) =100°. 又∵ ∠C=∠A, ∴ ∠C=100°. 【教师活动】巡视学生做题情况,及时纠正错误. 【学生活动】书写证明过程,先自主完成,再小组合作. 【例2】如图,在平行四边形中,,M为AB的中点.如图,连接DM,MC,试问直线DM和MC有何位置关系?请证明. 【教师活动】 (引发学生思考)解决直线DM和MC位置关系可以根据及M为AB的中点,分别证明△ADM和△BCM是等腰三角形,利用平行四边形的性质及等腰三角形的性质可证∠MDC=∠ADC,∠MCD=∠BCD,即可解决问题. 【学生活动】根据老师提供的思路,书写证明过程,总结证明两条直线垂直的证明方法. 【解】DM与MC互相垂直.证明如下: ∵ M是AB的中点,∴ AB=2AM. 又∵ AB=2AD,∴ AM=AD, ∴ ∠ADM=∠AMD. ∵ 四边形ABCD为平行四边形,∴ AB∥CD, ∴ ∠AMD=∠MDC,∴ ∠ADM=∠MDC, 即∠MDC=∠ADC. 同理,∠MCD=∠BCD. ∵ 四边形ABCD为平行四边形,∴ AD∥BC, ∴ ∠MCD+∠MDC=∠BCD+∠ADC=90°, ∴ ∠DMC=90°,∴ DM与MC互相垂直. 【例3】如图,在□ ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF. 【证明】∵ 四边形ABCD是平行四边形, ∴ AB=CD,AB ∥ CD, ∴ ∠BAE=∠DCF. 又∵ AE=CF, ∴ △ABE≌ △CDF. ∴ BE=DF. 【练习】如图,点G,E,F分别在平行四边形ABCD的边AD,DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP.求证:FP=EP. 【探索】要证明线段相等可以考虑证明它们所在的两个三角形全等,已知条件中有一组边相等,并且有一组公共边,只需找它们的夹角相等. 证明:∵ 四边形ABCD是平行四边形, ∴ AD∥BC,∴ ∠DGC=∠GCB. ∵ DG=DC,∴ ∠DGC=∠DCG, ∴ ∠DCG=∠GCB. ∵ ∠DCG+∠ECP=180°,∠GCB+∠FCP=180°, ∴ ∠ECP=∠FCP. 在△PCF和△PCE中, ∴ △PCF≌△PCE(SAS), ∴ PF=PE. 课堂练习 1.如图,在平行四边形ABCD中,CE⊥AB于点E,若∠A=125°, 则∠BCE的度数为( ) A.35° B.55° C.25° D.30° 2.如图所示,在□ABCD中,∠B=110°,延长AD至点F,延长CD至点E,连接EF,则∠E+∠F的值为( ) A.110° B.30° C.50° D.70° 3.在□ ABCD中,∠A∶∠B=2∶3,则∠A= _______,∠B= ______,∠C= ______, ∠D= _______. 4.已知□ ABCD的周长为20 cm,且AD-AB=1 cm,则 AD= ,CD= . 5.已知平行四边形ABCD的周长为60 cm,两邻边AB,BC长的比为3∶2,求AB和BC的长度 . 6.如图所示,已知在平行四边形中,∠C=60°,于点E,DF⊥BC于点F. (1)求∠EDF的度数; (2)若AE=4,CF=7,求平行四边形ABCD的周长. 参考答案 1.A 2.D 3.72° 108° 72° 108° 4.5.5 cm 4.5 cm 5.解:∵ 在□ABCD中, 对边相等, 又□ABCD的周长为60 cm, ∴ AB + BC=30 cm. 又AB:BC=3:2, 即AB=1.5BC. 则1.5BC+BC=30, 解得BC=12 (cm). ∴ AB=1.5×12=18(cm). 6.解:(1)∵ 四边形ABCD是平行四边形, ∴ AB∥CD,∠A=∠C=60°,∠C+∠B=180°. ∵ ∠C=60°, ∴ ∠B=180°-∠C=120°. ∵ DE⊥AB,DF⊥BC, ∴ ∠DEB=∠DFB=90°, ∴ ∠EDF=360°-∠DEB-∠DFB-∠B=60°. (2) 在Rt△ADE和Rt△CDF中,∠A=∠C=60°, ∴ ∠ADE=∠CDF=30°, ∴ AD=2AE=8,CD=2CF=14, ∴ 平行四边形ABCD的周长为2×(8+14)=44. 课堂小结 平行四边形定义两组对边分别平行的四边形叫做平行四边形表示法平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线性质平行四边形的对边相等,对角相等,相邻两角互补
布置作业 教材第78页练习. 板书设计 平行四边形边、角的性质 教学反思 教学反思 教学反思 教学反思 教学反思 教学反思
19.2 平行四边形
第1课时 平行四边形边、角的性质
教学目标 1.引导学生理解平行四边形的定义,掌握平行四边形对边相等、对角相等的性质,并能够证明. 2.经历平行四边形性质的探究、归纳过程,让学生体会通过观察、猜想、操作、论证获得数学知识的方法. 教学重难点 重点:平行四边形的性质. 难点:证明平行四边形的性质. 教学过程 复习巩固 观察图形,说出下列图形边的位置有什么特征? 两组对边分别平行的四边形叫做平行四边形. 导入新课 观察这些图片,它们是否都有平行四边形的形象. 探究新知 拼一拼 取两个全等的三角形纸片,将它们相等的一边重合,得到一个四边形. 【学生活动】动手操作,实际演示. 【总结】 1.定义 两组对边分别平行的四边形叫做平行四边形. 2.几何语言 3. 符号: 如平行四边形,记作:□; 读作:平行四边形 注意:顶点字母按照顺时针或者逆时针方向排序. 【教师活动】通过定义,你能迅速地画出一个平行四边形吗?我们可以得到平行四边形的哪些性质? 【学生活动】学生根据画出的平行四边形先进行测量,独立思考,再踊跃回答. 【教师活动】利用几何画板演示不同的平行四边形的边、对角之间的关系,在操作中启发学生思考. 平行四边形的边具有哪些性质?平行四边形的角具有哪些性质?说说你的理由. 平行四边形的对边相等;平行四边形的对角相等. 理由: 已知:如图,四边形ABCD是平行四边形. 求证:AB=CD,BC=DA. 证明:连接AC. ∵ 四边形ABCD是平行四边形, ∴ AB∥CD,BC∥DA. ∴ ∠1=∠2,∠3=∠4. 在△ABC和△CDA中, ∵∠1=∠2,AC=CA,∠3=∠4, ∴ △ABC≌△CDA(ASA). ∴ AB=CD,BC=DA. ∠DAB=∠DCB,∠B=∠D. 【教师引导】利用问题的形式引导学生,我们证明线段或者角相等的方法有哪些?图中没有三角形怎么办?全等三角形的判定有哪些? 【学生活动】根据老师的引导,整理整体思路,先小组合作交流,写出已知和求证,其中两名学生在黑板上板演解题过程. 【板书总结】师生共同总结平行四边形的边、角性质. 平行四边形的对边平行. 几何语言:∵ 四边形ABCD是平行四边形, ∴ AB∥CD,BC∥AD. 性质定理1:平行四边形的对边相等. 几何语言:∵ 四边形ABCD是平行四边形, ∴ AB=CD,BC=AD. 性质定理2:平行四边形的对角相等. 几何语言:∵ 四边形ABCD是平行四边形, ∴ ∠A=∠C,∠B=∠D. 【例1】已知:如图,□ABCD中,BE平分∠ABC交AD于点E. (1)如果AE=2,求CD的长; (2)如果∠AEB=40°,求∠C的度数. 【解】 (1)∵ BE平分∠ABC,且AD∥BC, ∴ ∠ABE=∠EBC=∠AEB. ∴ AB=AE=2. 又∵ CD=AB, ∴ CD=2. (2)由(1)知 ∠AEB =∠ABE=40°, ∴ ∠A=180°-(40°+40°) =100°. 又∵ ∠C=∠A, ∴ ∠C=100°. 【教师活动】巡视学生做题情况,及时纠正错误. 【学生活动】书写证明过程,先自主完成,再小组合作. 【例2】如图,在平行四边形中,,M为AB的中点.如图,连接DM,MC,试问直线DM和MC有何位置关系?请证明. 【教师活动】 (引发学生思考)解决直线DM和MC位置关系可以根据及M为AB的中点,分别证明△ADM和△BCM是等腰三角形,利用平行四边形的性质及等腰三角形的性质可证∠MDC=∠ADC,∠MCD=∠BCD,即可解决问题. 【学生活动】根据老师提供的思路,书写证明过程,总结证明两条直线垂直的证明方法. 【解】DM与MC互相垂直.证明如下: ∵ M是AB的中点,∴ AB=2AM. 又∵ AB=2AD,∴ AM=AD, ∴ ∠ADM=∠AMD. ∵ 四边形ABCD为平行四边形,∴ AB∥CD, ∴ ∠AMD=∠MDC,∴ ∠ADM=∠MDC, 即∠MDC=∠ADC. 同理,∠MCD=∠BCD. ∵ 四边形ABCD为平行四边形,∴ AD∥BC, ∴ ∠MCD+∠MDC=∠BCD+∠ADC=90°, ∴ ∠DMC=90°,∴ DM与MC互相垂直. 【例3】如图,在□ ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF. 【证明】∵ 四边形ABCD是平行四边形, ∴ AB=CD,AB ∥ CD, ∴ ∠BAE=∠DCF. 又∵ AE=CF, ∴ △ABE≌ △CDF. ∴ BE=DF. 【练习】如图,点G,E,F分别在平行四边形ABCD的边AD,DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP.求证:FP=EP. 【探索】要证明线段相等可以考虑证明它们所在的两个三角形全等,已知条件中有一组边相等,并且有一组公共边,只需找它们的夹角相等. 证明:∵ 四边形ABCD是平行四边形, ∴ AD∥BC,∴ ∠DGC=∠GCB. ∵ DG=DC,∴ ∠DGC=∠DCG, ∴ ∠DCG=∠GCB. ∵ ∠DCG+∠ECP=180°,∠GCB+∠FCP=180°, ∴ ∠ECP=∠FCP. 在△PCF和△PCE中, ∴ △PCF≌△PCE(SAS), ∴ PF=PE. 课堂练习 1.如图,在平行四边形ABCD中,CE⊥AB于点E,若∠A=125°, 则∠BCE的度数为( ) A.35° B.55° C.25° D.30° 2.如图所示,在□ABCD中,∠B=110°,延长AD至点F,延长CD至点E,连接EF,则∠E+∠F的值为( ) A.110° B.30° C.50° D.70° 3.在□ ABCD中,∠A∶∠B=2∶3,则∠A= _______,∠B= ______,∠C= ______, ∠D= _______. 4.已知□ ABCD的周长为20 cm,且AD-AB=1 cm,则 AD= ,CD= . 5.已知平行四边形ABCD的周长为60 cm,两邻边AB,BC长的比为3∶2,求AB和BC的长度 . 6.如图所示,已知在平行四边形中,∠C=60°,于点E,DF⊥BC于点F. (1)求∠EDF的度数; (2)若AE=4,CF=7,求平行四边形ABCD的周长. 参考答案 1.A 2.D 3.72° 108° 72° 108° 4.5.5 cm 4.5 cm 5.解:∵ 在□ABCD中, 对边相等, 又□ABCD的周长为60 cm, ∴ AB + BC=30 cm. 又AB:BC=3:2, 即AB=1.5BC. 则1.5BC+BC=30, 解得BC=12 (cm). ∴ AB=1.5×12=18(cm). 6.解:(1)∵ 四边形ABCD是平行四边形, ∴ AB∥CD,∠A=∠C=60°,∠C+∠B=180°. ∵ ∠C=60°, ∴ ∠B=180°-∠C=120°. ∵ DE⊥AB,DF⊥BC, ∴ ∠DEB=∠DFB=90°, ∴ ∠EDF=360°-∠DEB-∠DFB-∠B=60°. (2) 在Rt△ADE和Rt△CDF中,∠A=∠C=60°, ∴ ∠ADE=∠CDF=30°, ∴ AD=2AE=8,CD=2CF=14, ∴ 平行四边形ABCD的周长为2×(8+14)=44. 课堂小结 平行四边形定义两组对边分别平行的四边形叫做平行四边形表示法平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线性质平行四边形的对边相等,对角相等,相邻两角互补
布置作业 教材第78页练习. 板书设计 平行四边形边、角的性质 教学反思 教学反思 教学反思 教学反思 教学反思 教学反思
