19.2平行四边形(第5课时) 教案 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.2平行四边形(第5课时) 教案 沪科版初中数学八年级(下) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览


文档简介
第19章 四边形
19.2 平行四边形
第5课时 利用对角线判定平行四边形
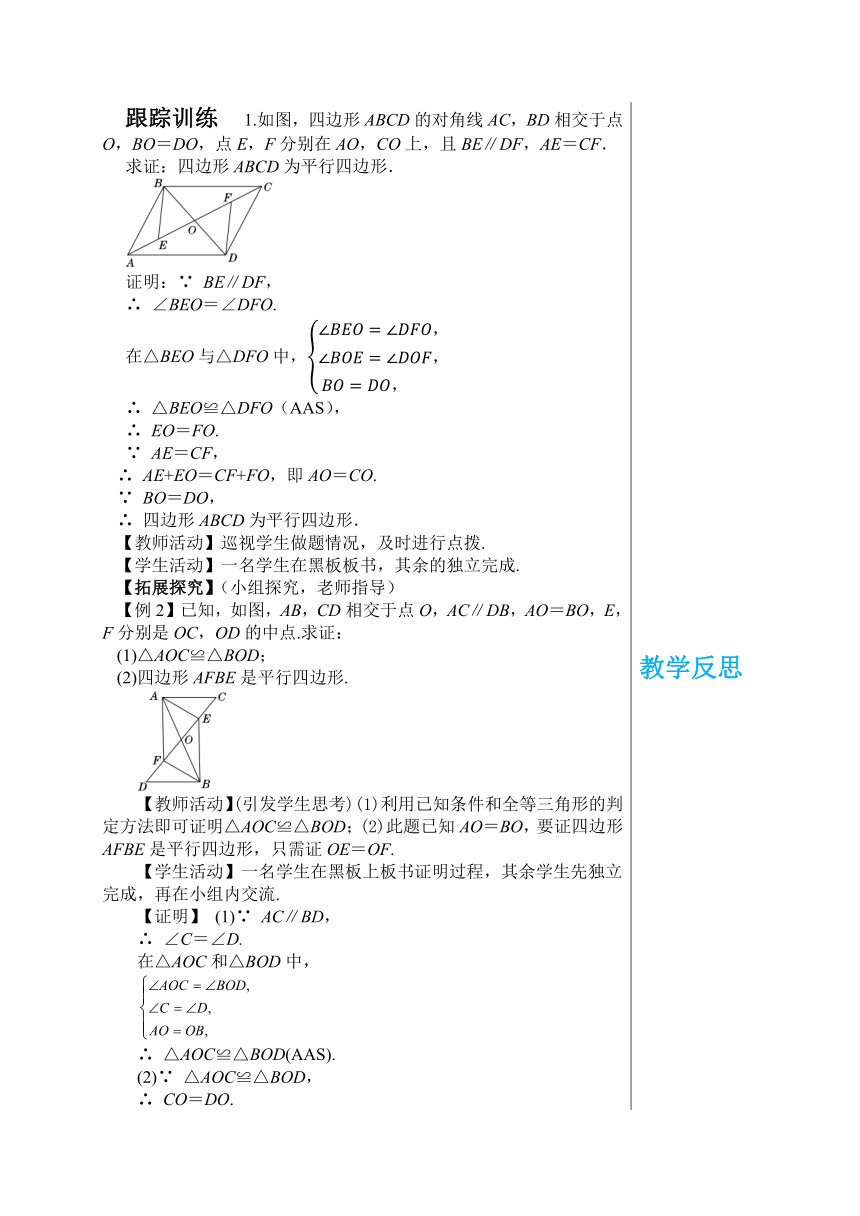
教学目标 1.让学生探索并学会证明“对角线互相平分的四边形是平行四边形”. 2.使学生能够应用平行四边形的判定定理解决问题. 教学重难点 重点: 运用对角线互相平分的四边形是平行四边形这一定理. 难点:平行四边形的性质和判定的综合运用. 教学过程 新课引入 问题 如图,作两条直线相交于点O,在直线上截取OA=OC,在直线上截取OB=OD,连接AB,BC,CD,DA.这样画出的四边形ABCD的对角线互相平分,它是平行四边形吗 为什么 大胆猜想,你可以给出证明吗? 猜想:四边形ABCD是平行四边形. 探究新知 定理:对角线互相平分的四边形是平行四边形. 【教师活动】分析题目中的已知条件和求证的结论,引导学生利用平行四边形的定义、判定定理1、判定定理2分别进行证明. 【学生活动】根据老师的分析,写出已知和求证,分析三种判定方法,选择一种自己认为较好的方法写出证明过程,在小组内交流总结. 已知:如图,四边形ABCD,AC,BD交于点O且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形. 证明:如图, ∵ 在△AOB与△COD中, ∴ △AOB≌△COD(SAS), ∴ AB=CD ,∠3=∠4, ∴ AB∥CD , ∴ 四边形ABCD是平行四边形. 【总结】 定理:对角线互相平分的四边形是平行四边形. 符号语言:∵ OA=OC,OB=OD, ∴ 四边形ABCD是平行四边形. 例题讲解 【例1】已知,如图,在平行四边形ABCD中,点E,F在对角线AC上,并且AE=CF. 求证:四边形BFDE是平行四边形. 【证明】如图,连接BD交AC于点 O. ∵ 四边形ABCD是平行四边形, ∴ OA=OC,OB=OD. 又∵ AE=CF, ∴ OA-AE=OC-CF, ∴ OE=OF. ∵ OB=OD, ∴ 四边形BFDE是平行四边形. 【教师活动】分析题目中的条件,引导学生连接BD,利用平行四边形的性质证明OB=OD,OA=OC,再进一步证明OE=OF. 【学生活动】独立完成证明过程,总结证明的方法,交流自己在做题中发现的规律. 【总结】在证明一个四边形是平行四边形时,若原图中有其中一条对角线,则通常利用对角线互相平分证明四边形是平行四边形. 跟踪训练 1.如图,四边形ABCD的对角线AC,BD相交于点O,BO=DO,点E,F分别在AO,CO上,且BE∥DF,AE=CF. 求证:四边形ABCD为平行四边形. 证明:∵ BE∥DF, ∴ ∠BEO=∠DFO. 在△BEO与△DFO中, ∴ △BEO≌△DFO(AAS), ∴ EO=FO. ∵ AE=CF, ∴ AE+EO=CF+FO,即AO=CO. ∵ BO=DO, ∴ 四边形ABCD为平行四边形. 【教师活动】巡视学生做题情况,及时进行点拨. 【学生活动】一名学生在黑板板书,其余的独立完成. 【拓展探究】(小组探究,老师指导) 【例2】已知,如图,AB,CD相交于点O,AC∥DB,AO=BO,E,F分别是OC,OD的中点.求证: (1)△AOC≌△BOD; (2)四边形AFBE是平行四边形. 【教师活动】(引发学生思考)(1)利用已知条件和全等三角形的判定方法即可证明△AOC≌△BOD;(2)此题已知AO=BO,要证四边形AFBE是平行四边形,只需证OE=OF. 【学生活动】一名学生在黑板上板书证明过程,其余学生先独立完成,再在小组内交流. 【证明】 (1)∵ AC∥BD, ∴ ∠C=∠D. 在△AOC和△BOD中, ∴ △AOC≌△BOD(AAS). (2)∵ △AOC≌△BOD, ∴ CO=DO. ∵ E,F分别是OC,OD的中点, ∴ OF=OD,OE=OC, ∴ EO=FO. 又∵ AO=BO, ∴ 四边形AFBE是平行四边形. 【总结】(学生总结,老师点评)在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.熟练掌握平行四边形的判定定理是解决问题的关键. 跟踪训练 2.如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO,并延长交CB的延长线于点F,∠E=∠F,AD=BC. (1)求证:O是线段AC的中点: (2)连接AF、EC,证明四边形AFCE是平行四边形. 证明:(1)∵ ∠E=∠F, ∴ AD∥BC. ∵ AD=BC, ∴ 四边形ABCD是平行四边形, ∴ AC,BD互相平分. 即O是线段AC的中点. (2)∵ AD∥BC, ∴ ∠EAC=∠FCA. 在△OAE和△OCF中, ∴ △OAE≌△OCF(ASA). ∴ OE=OF. 又∵ OA=OC, ∴ 四边形AFCE是平行四边形. 【教师活动】巡视学生做题情况,及时进行点拨,引导学生正确书写证明过程. 【学生活动】先在小组内交流证题思路,再按照思路写出证明过程,最后小组与小组交流,整理证明过程. 课堂练习 1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ) A.OA=OC,OB=OD B.AB=CD,AO=CO C.AB=CD,AD=BC D.∠BAD=∠BCD,AB∥CD 2.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.这种方法的依据是( ) A.对角线互相平分的四边形是平行四边形 B.一组对边平行且相等的四边形是平行四边形 C.两组对边分别相等的四边形是平行四边形 D.两组对边分别平行的四边形是平行四边形 3.如图,AC,BD是相交的两条线段,点O为它们的中点.当BD绕点O旋转时,连接AB,BC,CD,DA,所得到的四边形ABCD始终为 形. 4.如图,四边形ABCD的对角线交于点O,从下列条件①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个,使得四边形ABCD是平行四边形,则你选的两个条件是 .(填写一组序号即可) 5.如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,连接CF.四边形BDFC是平行四边形吗?证明你的结论. 参考答案 1.B 2.A 3.平行四边 4.①③(答案不唯一) 5.解:四边形BDFC是平行四边形.理由如下: ∵ ∠A=∠ABC=90°, ∴ ∠A+∠ABC=180°, ∴ BC∥AF, ∴ ∠BCE=∠FDE. ∵ E是CD中点, ∴ CE=DE. 在△BCE和△FDE中, ∴ △BCE≌△FDE(ASA), ∴ BE=EF. 又CE=DE, ∴ 四边形BDFC为平行四边形. 课堂小结 平行四边形的判定方法 布置作业 教材第82页练习. 板书设计 第5课时 利用对角线判定平行四边形 定理:对角线互相平分的四边形是平行四边形. 符号语言:∵ OA=OC,OB=OD, ∴ 四边形ABCD是平行四边形 . 教学反思 教学反思 教学反思 教学反思 教学反思
19.2 平行四边形
第5课时 利用对角线判定平行四边形
教学目标 1.让学生探索并学会证明“对角线互相平分的四边形是平行四边形”. 2.使学生能够应用平行四边形的判定定理解决问题. 教学重难点 重点: 运用对角线互相平分的四边形是平行四边形这一定理. 难点:平行四边形的性质和判定的综合运用. 教学过程 新课引入 问题 如图,作两条直线相交于点O,在直线上截取OA=OC,在直线上截取OB=OD,连接AB,BC,CD,DA.这样画出的四边形ABCD的对角线互相平分,它是平行四边形吗 为什么 大胆猜想,你可以给出证明吗? 猜想:四边形ABCD是平行四边形. 探究新知 定理:对角线互相平分的四边形是平行四边形. 【教师活动】分析题目中的已知条件和求证的结论,引导学生利用平行四边形的定义、判定定理1、判定定理2分别进行证明. 【学生活动】根据老师的分析,写出已知和求证,分析三种判定方法,选择一种自己认为较好的方法写出证明过程,在小组内交流总结. 已知:如图,四边形ABCD,AC,BD交于点O且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形. 证明:如图, ∵ 在△AOB与△COD中, ∴ △AOB≌△COD(SAS), ∴ AB=CD ,∠3=∠4, ∴ AB∥CD , ∴ 四边形ABCD是平行四边形. 【总结】 定理:对角线互相平分的四边形是平行四边形. 符号语言:∵ OA=OC,OB=OD, ∴ 四边形ABCD是平行四边形. 例题讲解 【例1】已知,如图,在平行四边形ABCD中,点E,F在对角线AC上,并且AE=CF. 求证:四边形BFDE是平行四边形. 【证明】如图,连接BD交AC于点 O. ∵ 四边形ABCD是平行四边形, ∴ OA=OC,OB=OD. 又∵ AE=CF, ∴ OA-AE=OC-CF, ∴ OE=OF. ∵ OB=OD, ∴ 四边形BFDE是平行四边形. 【教师活动】分析题目中的条件,引导学生连接BD,利用平行四边形的性质证明OB=OD,OA=OC,再进一步证明OE=OF. 【学生活动】独立完成证明过程,总结证明的方法,交流自己在做题中发现的规律. 【总结】在证明一个四边形是平行四边形时,若原图中有其中一条对角线,则通常利用对角线互相平分证明四边形是平行四边形. 跟踪训练 1.如图,四边形ABCD的对角线AC,BD相交于点O,BO=DO,点E,F分别在AO,CO上,且BE∥DF,AE=CF. 求证:四边形ABCD为平行四边形. 证明:∵ BE∥DF, ∴ ∠BEO=∠DFO. 在△BEO与△DFO中, ∴ △BEO≌△DFO(AAS), ∴ EO=FO. ∵ AE=CF, ∴ AE+EO=CF+FO,即AO=CO. ∵ BO=DO, ∴ 四边形ABCD为平行四边形. 【教师活动】巡视学生做题情况,及时进行点拨. 【学生活动】一名学生在黑板板书,其余的独立完成. 【拓展探究】(小组探究,老师指导) 【例2】已知,如图,AB,CD相交于点O,AC∥DB,AO=BO,E,F分别是OC,OD的中点.求证: (1)△AOC≌△BOD; (2)四边形AFBE是平行四边形. 【教师活动】(引发学生思考)(1)利用已知条件和全等三角形的判定方法即可证明△AOC≌△BOD;(2)此题已知AO=BO,要证四边形AFBE是平行四边形,只需证OE=OF. 【学生活动】一名学生在黑板上板书证明过程,其余学生先独立完成,再在小组内交流. 【证明】 (1)∵ AC∥BD, ∴ ∠C=∠D. 在△AOC和△BOD中, ∴ △AOC≌△BOD(AAS). (2)∵ △AOC≌△BOD, ∴ CO=DO. ∵ E,F分别是OC,OD的中点, ∴ OF=OD,OE=OC, ∴ EO=FO. 又∵ AO=BO, ∴ 四边形AFBE是平行四边形. 【总结】(学生总结,老师点评)在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.熟练掌握平行四边形的判定定理是解决问题的关键. 跟踪训练 2.如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO,并延长交CB的延长线于点F,∠E=∠F,AD=BC. (1)求证:O是线段AC的中点: (2)连接AF、EC,证明四边形AFCE是平行四边形. 证明:(1)∵ ∠E=∠F, ∴ AD∥BC. ∵ AD=BC, ∴ 四边形ABCD是平行四边形, ∴ AC,BD互相平分. 即O是线段AC的中点. (2)∵ AD∥BC, ∴ ∠EAC=∠FCA. 在△OAE和△OCF中, ∴ △OAE≌△OCF(ASA). ∴ OE=OF. 又∵ OA=OC, ∴ 四边形AFCE是平行四边形. 【教师活动】巡视学生做题情况,及时进行点拨,引导学生正确书写证明过程. 【学生活动】先在小组内交流证题思路,再按照思路写出证明过程,最后小组与小组交流,整理证明过程. 课堂练习 1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ) A.OA=OC,OB=OD B.AB=CD,AO=CO C.AB=CD,AD=BC D.∠BAD=∠BCD,AB∥CD 2.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.这种方法的依据是( ) A.对角线互相平分的四边形是平行四边形 B.一组对边平行且相等的四边形是平行四边形 C.两组对边分别相等的四边形是平行四边形 D.两组对边分别平行的四边形是平行四边形 3.如图,AC,BD是相交的两条线段,点O为它们的中点.当BD绕点O旋转时,连接AB,BC,CD,DA,所得到的四边形ABCD始终为 形. 4.如图,四边形ABCD的对角线交于点O,从下列条件①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个,使得四边形ABCD是平行四边形,则你选的两个条件是 .(填写一组序号即可) 5.如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,连接CF.四边形BDFC是平行四边形吗?证明你的结论. 参考答案 1.B 2.A 3.平行四边 4.①③(答案不唯一) 5.解:四边形BDFC是平行四边形.理由如下: ∵ ∠A=∠ABC=90°, ∴ ∠A+∠ABC=180°, ∴ BC∥AF, ∴ ∠BCE=∠FDE. ∵ E是CD中点, ∴ CE=DE. 在△BCE和△FDE中, ∴ △BCE≌△FDE(ASA), ∴ BE=EF. 又CE=DE, ∴ 四边形BDFC为平行四边形. 课堂小结 平行四边形的判定方法 布置作业 教材第82页练习. 板书设计 第5课时 利用对角线判定平行四边形 定理:对角线互相平分的四边形是平行四边形. 符号语言:∵ OA=OC,OB=OD, ∴ 四边形ABCD是平行四边形 . 教学反思 教学反思 教学反思 教学反思 教学反思
