19.4综合与实践 多边形的镶嵌 教案 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.4综合与实践 多边形的镶嵌 教案 沪科版初中数学八年级(下) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:55 | ||
图片预览


文档简介
第19章 四边形
19.4 综合与实践 多边形的镶嵌
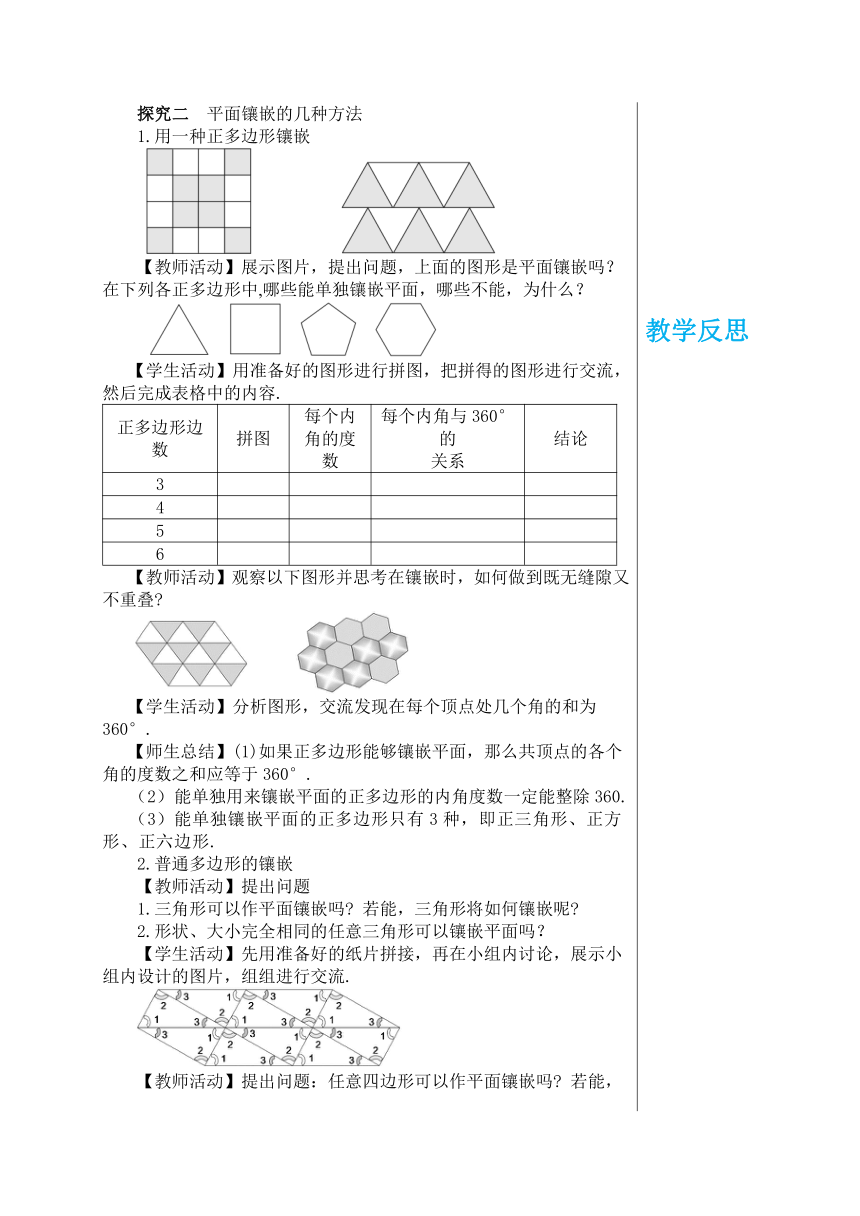
教学目标 1.了解平面图形镶嵌的含义,掌握哪些平面图形可以镶嵌,镶嵌的理由及简单的设计. 2.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌,并能运用这几种图形进行简单的计算. 3.经历探索多边形镶嵌的过程,进一步发展学生的合情推理能力,开发、培养学生创造性思维培养学生动手操作. 4.使学生进一步体会平面图形在现实生活中的广泛应用,体会数学与现实生活的密切联系,认识数学的应用价值. 教学重难点 重点:多边形能够镶嵌的条件. 难点:正多边形镶嵌的规律. 教学过程 导入新课 密铺其实源于生活,现在同学们已经知道“密铺中的学问”了,利用这些规律人们设计出了绚烂多彩的“密铺世界”.大家欣赏下列图片,了解本节的主要内容. 探究新知 探究一 平面镶嵌的定义 【学生活动】观察图片,理解平面镶嵌的定义. 【教师活动】根据拼图特征,引导学生总结出平面镶嵌的定义. 这种用形状相同或不相同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌. 探究二 平面镶嵌的几种方法 1.用一种正多边形镶嵌 【教师活动】展示图片,提出问题,上面的图形是平面镶嵌吗?在下列各正多边形中,哪些能单独镶嵌平面,哪些不能,为什么? 【学生活动】用准备好的图形进行拼图,把拼得的图形进行交流,然后完成表格中的内容. 正多边形边数拼图每个内角的度数每个内角与360°的 关系结论3456
【教师活动】观察以下图形并思考在镶嵌时,如何做到既无缝隙又不重叠 【学生活动】分析图形,交流发现在每个顶点处几个角的和为360°. 【师生总结】(1)如果正多边形能够镶嵌平面,那么共顶点的各个角的度数之和应等于360°. (2)能单独用来镶嵌平面的正多边形的内角度数一定能整除360. (3)能单独镶嵌平面的正多边形只有3种,即正三角形、正方形、正六边形. 2.普通多边形的镶嵌 【教师活动】提出问题 1.三角形可以作平面镶嵌吗 若能,三角形将如何镶嵌呢 2.形状、大小完全相同的任意三角形可以镶嵌平面吗? 【学生活动】先用准备好的纸片拼接,再在小组内讨论,展示小组内设计的图片,组组进行交流. 【教师活动】提出问题:任意四边形可以作平面镶嵌吗 若能,四边形将如何镶嵌呢 【学生活动】小组内进行交流,根据平面镶嵌的定义进行分析,猜测. 【教师活动】利用图形进行讲解,如图,四边形ABCD中,因为∠A+∠B+∠C+∠D=360°,所以四边形也可以作平面镶嵌. 【学生活动】利用手中的纸片进行拼接,在小组内展示图片,交流拼接的图片. 【师生总结】从而发现:形状、大小完全相同的平面图形能够镶嵌平面的有:任意三角形、任意四边形. 探究三 两种正多边形的组合镶嵌平面 【教师活动】跟学生展示问题,列举以下组合:提出两个问题. 1.想一想:哪些正多边形可以组合镶嵌. 2.当围绕一点拼在一起的几个正多边形的内角和加在一起恰好组成一个周角时,就能镶嵌一个平面图形,那么哪些正多边形可以进行镶嵌呢? 下列多边形组合,能够密铺平面的是 (1)正三角形与正六边形; (2)正三角形与正方形; (3)正方形与正八边形; (4)正六边形与正八边形; (5)正三角形、正方形与正六边形. 【学生活动】先根据自己的理解,小组内讨论,展示自己画出的镶嵌图片. 【师生总结】1.镶嵌的要求:无缝隙,不重叠. 2.多边形能否镶嵌的条件:每个顶点处几个角的和为360°. 【教师活动】 请你欣赏:两种以上的多边形设计的镶嵌图案. 例题讲解 【例1】用边长相同的正三边形和正四边形做平面密铺,有几种可能?为什么? 【解】设在一个顶点周围有x个正三角形的角、y个正方形的角.那么,这些角的和应满足方程: x·60°+y·90°=360°, 即2 x +3y=12, 这个方程的正整数解为 所以这样的平面镶嵌存在,即在它的每一个顶点周围有3个正三角形和2个正方形. 【教师活动】根据密铺的条件,引导学生设出未知数,列出方程,巡视学生做题,及时纠正出现的错误. 【学生活动】根据老师的指导,列方程求解,并讨论为什么必须是方程的正整数解. 跟踪训练 1.用边长相同的正四边形和正八边形做平面密铺,有几种可能?为什么? 解:设在一个顶点周围有x个正四边形,y个正八边形,
则x·90°+y·135°=360°, 即2x+3y=8. 这个方程的正整数解为 所以用正四边形和正八边形做平面密铺即在它的一个顶点周围用1个正四边形配2个正八边形. 【例2】用边长相同的正三边形和正六边形做平面密铺,有几种可能?为什么? 【解】设在一个顶点周围有m个正三角形的角,n个正六边形的角.那么,应有m·60°+n·120°=360°,即m+2n=6. 这个方程的正整数解为或者 用正三边形和正四边形做平面密铺在它的一个顶点周围用4个正三边形配1个正六边形或者用2个正三边形配2个正六边形. 【教师活动】提出问题:在它的每一个顶点周围有几个正三角形和几个正六边形 让学生尝试自己解决问题. 【学生活动】根据老师的提示,自己列方程求解,再在小组内交流,找出所列方程的正整数解,总结这类题的解题方法. 【师生总结】解决密铺问题,先根据题意列出方程,再求方程的正整数解. 跟踪训练 2.如果用正三角形和正十二边形作平面镶嵌有几种可能的情形 为什么 解:设在一个顶点周围有m个正三角形的角、n个正十二边形的角,则有 m·60°+n·150°=360°,∴ 2m+5n=12, ∵ m,n为正整数, ∴ 这个方程的正整数解为 课堂练习 1.用边长相等的正多边形进行密铺,下列正多边形能和正八边形密铺的是( )
A.正三角形 B.正六边形 C.正五边形 D.正四边形
2.下列多边形的组合中,能够铺满地面的是( )
A.正三角形和正五边形 B.正六边形和正三角形
C.正五边形和正八边形 D.正八边形和正三角形
3.用若干个同样大小的正三角形能拼成的图形是( )
A.正八边形 B.正六边形 C.正五边形 D.正方形
4.如图是正在铺设的人行道上地板砖的部分,由正六边形和四边形镶嵌而成的图形,则图中的四边形ABCD中的∠BAD的度数是 度. 5.若一个正多边形的每个外角都等于45°,则用这种多边形能铺满地面吗?(填“能”或“不能”)答: . 6.在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题: (1)用一种正多边形镶嵌平面 例如,用6个全等的正三角形镶嵌平面,摆放方案如图所示: 若用m个全等的正n边形镶嵌平面,求出m,n应满足的关系式; (2)用两种正多边形镶嵌平面 若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案; (3)用多种正多边形镶嵌平面 若镶嵌时每个顶点处的正多边形有n个,设这n个正多边形的边数分别为x1,x2,…,xn,求出x1,x2,…,xn应满足的关系式.(用含n的式子表示) 参考答案 1.D 2.B 3.B 4.60 解析:正六边形内角和为(6﹣2)×180°=720°, 所以每个内角度数720°÷6=120°,∴ ∠BAD=180°﹣120°=60°. 5.不能 解析:∵ 正多边形每个内角180°﹣45°=135°,∴ 不能整除360°,∴ 不能密铺. 6.解:(1)∵ 正n边形的内角和为180°(n﹣2),
∴ 每个内角的度数为 .由题意得m =360°,
整理,得m(n﹣2)=2n,即2m+2n=mn. (2)边长相等的正三角形和正方形镶嵌平面,两种不同的摆放方案, 图所示: (3)由题意得=360°, 整理,得=2, 即. 课堂小结 1.平面镶嵌的定义 2.镶嵌满足的条件 3.多边形的镶嵌 板书设计 19.4 综合与实践 多边形的镶嵌 探究一 平面镶嵌的定义 探究二 平面镶嵌的几种方法 1.用一种多边形镶嵌 2.普通多边形的镶嵌 3.用两种多边形镶嵌 教学反思 教学反思 教学反思 教学反思 教学反思
19.4 综合与实践 多边形的镶嵌
教学目标 1.了解平面图形镶嵌的含义,掌握哪些平面图形可以镶嵌,镶嵌的理由及简单的设计. 2.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌,并能运用这几种图形进行简单的计算. 3.经历探索多边形镶嵌的过程,进一步发展学生的合情推理能力,开发、培养学生创造性思维培养学生动手操作. 4.使学生进一步体会平面图形在现实生活中的广泛应用,体会数学与现实生活的密切联系,认识数学的应用价值. 教学重难点 重点:多边形能够镶嵌的条件. 难点:正多边形镶嵌的规律. 教学过程 导入新课 密铺其实源于生活,现在同学们已经知道“密铺中的学问”了,利用这些规律人们设计出了绚烂多彩的“密铺世界”.大家欣赏下列图片,了解本节的主要内容. 探究新知 探究一 平面镶嵌的定义 【学生活动】观察图片,理解平面镶嵌的定义. 【教师活动】根据拼图特征,引导学生总结出平面镶嵌的定义. 这种用形状相同或不相同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌. 探究二 平面镶嵌的几种方法 1.用一种正多边形镶嵌 【教师活动】展示图片,提出问题,上面的图形是平面镶嵌吗?在下列各正多边形中,哪些能单独镶嵌平面,哪些不能,为什么? 【学生活动】用准备好的图形进行拼图,把拼得的图形进行交流,然后完成表格中的内容. 正多边形边数拼图每个内角的度数每个内角与360°的 关系结论3456
【教师活动】观察以下图形并思考在镶嵌时,如何做到既无缝隙又不重叠 【学生活动】分析图形,交流发现在每个顶点处几个角的和为360°. 【师生总结】(1)如果正多边形能够镶嵌平面,那么共顶点的各个角的度数之和应等于360°. (2)能单独用来镶嵌平面的正多边形的内角度数一定能整除360. (3)能单独镶嵌平面的正多边形只有3种,即正三角形、正方形、正六边形. 2.普通多边形的镶嵌 【教师活动】提出问题 1.三角形可以作平面镶嵌吗 若能,三角形将如何镶嵌呢 2.形状、大小完全相同的任意三角形可以镶嵌平面吗? 【学生活动】先用准备好的纸片拼接,再在小组内讨论,展示小组内设计的图片,组组进行交流. 【教师活动】提出问题:任意四边形可以作平面镶嵌吗 若能,四边形将如何镶嵌呢 【学生活动】小组内进行交流,根据平面镶嵌的定义进行分析,猜测. 【教师活动】利用图形进行讲解,如图,四边形ABCD中,因为∠A+∠B+∠C+∠D=360°,所以四边形也可以作平面镶嵌. 【学生活动】利用手中的纸片进行拼接,在小组内展示图片,交流拼接的图片. 【师生总结】从而发现:形状、大小完全相同的平面图形能够镶嵌平面的有:任意三角形、任意四边形. 探究三 两种正多边形的组合镶嵌平面 【教师活动】跟学生展示问题,列举以下组合:提出两个问题. 1.想一想:哪些正多边形可以组合镶嵌. 2.当围绕一点拼在一起的几个正多边形的内角和加在一起恰好组成一个周角时,就能镶嵌一个平面图形,那么哪些正多边形可以进行镶嵌呢? 下列多边形组合,能够密铺平面的是 (1)正三角形与正六边形; (2)正三角形与正方形; (3)正方形与正八边形; (4)正六边形与正八边形; (5)正三角形、正方形与正六边形. 【学生活动】先根据自己的理解,小组内讨论,展示自己画出的镶嵌图片. 【师生总结】1.镶嵌的要求:无缝隙,不重叠. 2.多边形能否镶嵌的条件:每个顶点处几个角的和为360°. 【教师活动】 请你欣赏:两种以上的多边形设计的镶嵌图案. 例题讲解 【例1】用边长相同的正三边形和正四边形做平面密铺,有几种可能?为什么? 【解】设在一个顶点周围有x个正三角形的角、y个正方形的角.那么,这些角的和应满足方程: x·60°+y·90°=360°, 即2 x +3y=12, 这个方程的正整数解为 所以这样的平面镶嵌存在,即在它的每一个顶点周围有3个正三角形和2个正方形. 【教师活动】根据密铺的条件,引导学生设出未知数,列出方程,巡视学生做题,及时纠正出现的错误. 【学生活动】根据老师的指导,列方程求解,并讨论为什么必须是方程的正整数解. 跟踪训练 1.用边长相同的正四边形和正八边形做平面密铺,有几种可能?为什么? 解:设在一个顶点周围有x个正四边形,y个正八边形,
则x·90°+y·135°=360°, 即2x+3y=8. 这个方程的正整数解为 所以用正四边形和正八边形做平面密铺即在它的一个顶点周围用1个正四边形配2个正八边形. 【例2】用边长相同的正三边形和正六边形做平面密铺,有几种可能?为什么? 【解】设在一个顶点周围有m个正三角形的角,n个正六边形的角.那么,应有m·60°+n·120°=360°,即m+2n=6. 这个方程的正整数解为或者 用正三边形和正四边形做平面密铺在它的一个顶点周围用4个正三边形配1个正六边形或者用2个正三边形配2个正六边形. 【教师活动】提出问题:在它的每一个顶点周围有几个正三角形和几个正六边形 让学生尝试自己解决问题. 【学生活动】根据老师的提示,自己列方程求解,再在小组内交流,找出所列方程的正整数解,总结这类题的解题方法. 【师生总结】解决密铺问题,先根据题意列出方程,再求方程的正整数解. 跟踪训练 2.如果用正三角形和正十二边形作平面镶嵌有几种可能的情形 为什么 解:设在一个顶点周围有m个正三角形的角、n个正十二边形的角,则有 m·60°+n·150°=360°,∴ 2m+5n=12, ∵ m,n为正整数, ∴ 这个方程的正整数解为 课堂练习 1.用边长相等的正多边形进行密铺,下列正多边形能和正八边形密铺的是( )
A.正三角形 B.正六边形 C.正五边形 D.正四边形
2.下列多边形的组合中,能够铺满地面的是( )
A.正三角形和正五边形 B.正六边形和正三角形
C.正五边形和正八边形 D.正八边形和正三角形
3.用若干个同样大小的正三角形能拼成的图形是( )
A.正八边形 B.正六边形 C.正五边形 D.正方形
4.如图是正在铺设的人行道上地板砖的部分,由正六边形和四边形镶嵌而成的图形,则图中的四边形ABCD中的∠BAD的度数是 度. 5.若一个正多边形的每个外角都等于45°,则用这种多边形能铺满地面吗?(填“能”或“不能”)答: . 6.在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题: (1)用一种正多边形镶嵌平面 例如,用6个全等的正三角形镶嵌平面,摆放方案如图所示: 若用m个全等的正n边形镶嵌平面,求出m,n应满足的关系式; (2)用两种正多边形镶嵌平面 若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案; (3)用多种正多边形镶嵌平面 若镶嵌时每个顶点处的正多边形有n个,设这n个正多边形的边数分别为x1,x2,…,xn,求出x1,x2,…,xn应满足的关系式.(用含n的式子表示) 参考答案 1.D 2.B 3.B 4.60 解析:正六边形内角和为(6﹣2)×180°=720°, 所以每个内角度数720°÷6=120°,∴ ∠BAD=180°﹣120°=60°. 5.不能 解析:∵ 正多边形每个内角180°﹣45°=135°,∴ 不能整除360°,∴ 不能密铺. 6.解:(1)∵ 正n边形的内角和为180°(n﹣2),
∴ 每个内角的度数为 .由题意得m =360°,
整理,得m(n﹣2)=2n,即2m+2n=mn. (2)边长相等的正三角形和正方形镶嵌平面,两种不同的摆放方案, 图所示: (3)由题意得=360°, 整理,得=2, 即. 课堂小结 1.平面镶嵌的定义 2.镶嵌满足的条件 3.多边形的镶嵌 板书设计 19.4 综合与实践 多边形的镶嵌 探究一 平面镶嵌的定义 探究二 平面镶嵌的几种方法 1.用一种多边形镶嵌 2.普通多边形的镶嵌 3.用两种多边形镶嵌 教学反思 教学反思 教学反思 教学反思 教学反思
