教学课件:七下·湘教3.3 公式法 第1课时 利用平方差公式进行因式分解
文档属性
| 名称 | 教学课件:七下·湘教3.3 公式法 第1课时 利用平方差公式进行因式分解 |

|
|
| 格式 | pptx | ||
| 文件大小 | 762.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第 3 章 因式分解
第3章 因式分解
3.3 公式法
第1课时 利用平方差公式进行因式分解
学 习 目 标
1
2
理解用平方差公式进行因式分解,并能熟练地运用平方差公式分解因式.(重点)
能综合运用提公因式法和平方差公式对多项式
进行因式分解.(难点)
知识讲解
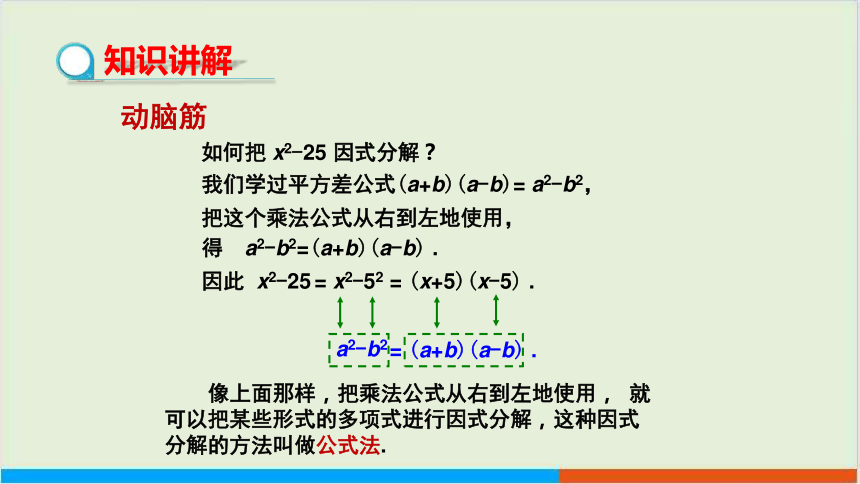
如何把 x2-25 因式分解?
动脑筋
我们学过平方差公式(a+b)(a-b)= a2-b2,
把这个乘法公式从右到左地使用,
得 a2-b2=(a+b)(a-b) .
因此 x2-25
= x2-52
= (x+5)(x-5) .
a2-b2
= (a+b)(a-b) .
像上面那样,把乘法公式从右到左地使用, 就可以把某些形式的多项式进行因式分解,这种因式分解的方法叫做公式法.
平方差公式法分解因式
语言叙述:两个数的平方差,等于这两个数的和与这两个数的差的积.
注意:公式中的既可以是单项式,也可以是多项式.
能用平方差公式分解因式的多项式的特点
多项式是二项式,两项都能写成平方的形式,且符号相反.
下列多项式能否用平方差公式来分解因式,如果能,请将其转化成( )2-( )2的形式.
(1) 2 -81
(2) 1 -162
(3) 42+9
(4
(5)
= 2 -92
= 12-(4 )2
不能转化为平方差形式
不能转化为平方差形式
试一试
例1 把25x2-4y2 因式分解.
分析 25x2= ( 5x) 2 ,4y2 = ( 2y )2 ,25x2 - 4y2 = ( 5x)2- ( 2y) 2 ,原式即可用平方差公式进行因式分解.
解: 25x2-4y2 = (5x)2-(2y)2
= (5x+2y)(5x-2y).
例2 把 (x+y)2-(x-y)2 因式分解 .
分析:将(x+y)看成a,(x-y)看成b,原式即可用平方差公式进行因式分解.
解: (x+y)2-(x-y)2
= [(x+y)+(x-y)][(x+y)-(x-y)]
= 2x·2y
= 4xy.
例3 把 x4-y4 因式分解 .
解: x4-y4
=
= ()( )
= ()( )( ).
注意:在因式分解时,必须进行到每一个因式都不能分解为止.
例4 把x3y2-x5 因式分解.
分析 x3y2-x5有公因式x3,应先提出公因式,再进一步进行因式分解.
解: x3y2-x5
= x3(y2-x2)
= x3(y+x)(y-x).
例5 因式分解:
解:原式
注意:把括号看成一个整体.
1.具有平方差形式的多项式才可运用平方差公式分解因式.
2.公式中的字母 可以是单项式,也可以是多项式,应视具体情形灵活运用.
3.若多项式中有公因式,应先提取公因式,然后再进一步分解因式.
4.分解因式要彻底.要注意每一个因式的形式要最简,直到不能再分解为止.
结论
随堂训练
1.判断正误:
( )
( )
( )
( )
√
×
×
×
2.分解因式(2x+3)2 -x2的结果是( )
A.3(x2+4x+3) B.3(x2+2x+3)
C.(3x+3)(x+3) D.3(x+1)(x+3)
D
3.若a+b=3,a-b=7,则b2-a2的值为( )
A.-21 B.21 C.-10 D.10
A
4.用平方差公式进行简便计算:
(1)38 -37 ;(2)213 -87 ;
(3)229 -171 ;(4)91×89.
解:(1)38 -37 =(38+37)(38-37)=75.
(2)213 -87 =(213+87)(213-87)=300×126=37800.
(3)229 -171 =(229+171)(229-171)
=400×58=23200.
(4)91×89=(90+1)(90-1)
=90 -1=8100-1=8099.
5.分解因式:
.
解:
)
6.如图,大小两圆的圆心相同,已知它们的半径分别是 cm和 cm,求它们所围成的环形的面积.如果=8.45cm,=3.45cm呢?
解: π R2- π r2
= π(R+r)(R-r)cm2
当R=8.45,r=3.45时,
原式=(8.45+3.45) ×(8.45-3.45) ×3.14
=186.83( cm2 ).
课堂小结
1.利用平方差公式分解因式: .
2.因式分解的步骤是:首先提取公因式,然后考虑用公式法.
3.因式分解应进行到每一个因式不能分解为止.
第 3 章 因式分解
第3章 因式分解
3.3 公式法
第1课时 利用平方差公式进行因式分解
学 习 目 标
1
2
理解用平方差公式进行因式分解,并能熟练地运用平方差公式分解因式.(重点)
能综合运用提公因式法和平方差公式对多项式
进行因式分解.(难点)
知识讲解
如何把 x2-25 因式分解?
动脑筋
我们学过平方差公式(a+b)(a-b)= a2-b2,
把这个乘法公式从右到左地使用,
得 a2-b2=(a+b)(a-b) .
因此 x2-25
= x2-52
= (x+5)(x-5) .
a2-b2
= (a+b)(a-b) .
像上面那样,把乘法公式从右到左地使用, 就可以把某些形式的多项式进行因式分解,这种因式分解的方法叫做公式法.
平方差公式法分解因式
语言叙述:两个数的平方差,等于这两个数的和与这两个数的差的积.
注意:公式中的既可以是单项式,也可以是多项式.
能用平方差公式分解因式的多项式的特点
多项式是二项式,两项都能写成平方的形式,且符号相反.
下列多项式能否用平方差公式来分解因式,如果能,请将其转化成( )2-( )2的形式.
(1) 2 -81
(2) 1 -162
(3) 42+9
(4
(5)
= 2 -92
= 12-(4 )2
不能转化为平方差形式
不能转化为平方差形式
试一试
例1 把25x2-4y2 因式分解.
分析 25x2= ( 5x) 2 ,4y2 = ( 2y )2 ,25x2 - 4y2 = ( 5x)2- ( 2y) 2 ,原式即可用平方差公式进行因式分解.
解: 25x2-4y2 = (5x)2-(2y)2
= (5x+2y)(5x-2y).
例2 把 (x+y)2-(x-y)2 因式分解 .
分析:将(x+y)看成a,(x-y)看成b,原式即可用平方差公式进行因式分解.
解: (x+y)2-(x-y)2
= [(x+y)+(x-y)][(x+y)-(x-y)]
= 2x·2y
= 4xy.
例3 把 x4-y4 因式分解 .
解: x4-y4
=
= ()( )
= ()( )( ).
注意:在因式分解时,必须进行到每一个因式都不能分解为止.
例4 把x3y2-x5 因式分解.
分析 x3y2-x5有公因式x3,应先提出公因式,再进一步进行因式分解.
解: x3y2-x5
= x3(y2-x2)
= x3(y+x)(y-x).
例5 因式分解:
解:原式
注意:把括号看成一个整体.
1.具有平方差形式的多项式才可运用平方差公式分解因式.
2.公式中的字母 可以是单项式,也可以是多项式,应视具体情形灵活运用.
3.若多项式中有公因式,应先提取公因式,然后再进一步分解因式.
4.分解因式要彻底.要注意每一个因式的形式要最简,直到不能再分解为止.
结论
随堂训练
1.判断正误:
( )
( )
( )
( )
√
×
×
×
2.分解因式(2x+3)2 -x2的结果是( )
A.3(x2+4x+3) B.3(x2+2x+3)
C.(3x+3)(x+3) D.3(x+1)(x+3)
D
3.若a+b=3,a-b=7,则b2-a2的值为( )
A.-21 B.21 C.-10 D.10
A
4.用平方差公式进行简便计算:
(1)38 -37 ;(2)213 -87 ;
(3)229 -171 ;(4)91×89.
解:(1)38 -37 =(38+37)(38-37)=75.
(2)213 -87 =(213+87)(213-87)=300×126=37800.
(3)229 -171 =(229+171)(229-171)
=400×58=23200.
(4)91×89=(90+1)(90-1)
=90 -1=8100-1=8099.
5.分解因式:
.
解:
)
6.如图,大小两圆的圆心相同,已知它们的半径分别是 cm和 cm,求它们所围成的环形的面积.如果=8.45cm,=3.45cm呢?
解: π R2- π r2
= π(R+r)(R-r)cm2
当R=8.45,r=3.45时,
原式=(8.45+3.45) ×(8.45-3.45) ×3.14
=186.83( cm2 ).
课堂小结
1.利用平方差公式分解因式: .
2.因式分解的步骤是:首先提取公因式,然后考虑用公式法.
3.因式分解应进行到每一个因式不能分解为止.
