教学课件:七下·湘教4.3 平行线的性质
文档属性
| 名称 | 教学课件:七下·湘教4.3 平行线的性质 |

|
|
| 格式 | pptx | ||
| 文件大小 | 813.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:31:07 | ||
图片预览







文档简介
(共21张PPT)
第 4 章 相交线与平行线
4.3 平行线的性质
学习目标
1.掌握平行线的性质,会运用平行线的性质判
断角相等或互补;(重点)
2.能够根据平行线的性质进行简单的推理. (难点)
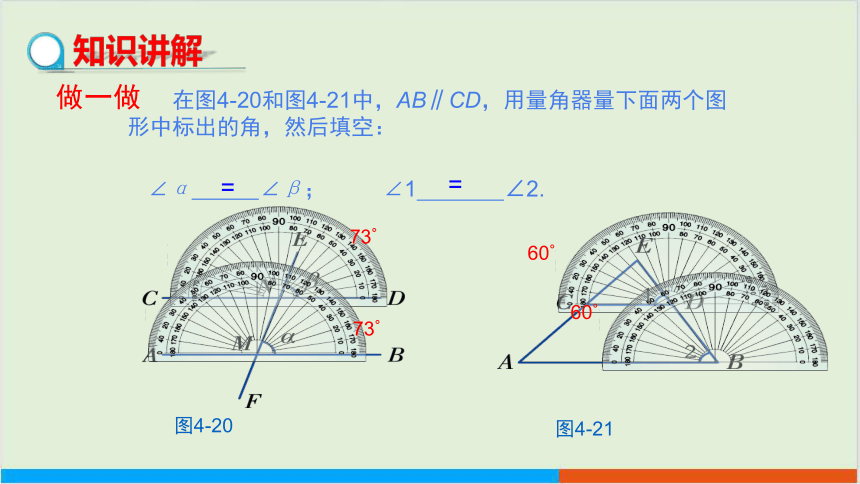
做一做
∠α ∠β; ∠1 ∠2.
图4-20
=
=
在图4-20和图4-21中,AB∥CD,用量角器量下面两个图形中标出的角,然后填空:
73°
73°
60°
60°
图4-21
知识讲解
平行线的性质1:两条平行直线被第三条直线所截,
同位角___.
相等
b
1
2
a
c
5
6
7
8
3
4
简单说成:两直线平行,同位角相等.
∴∠1=∠5 (两直线平行,同位角相等).
∵a∥b(已知),
应用格式:
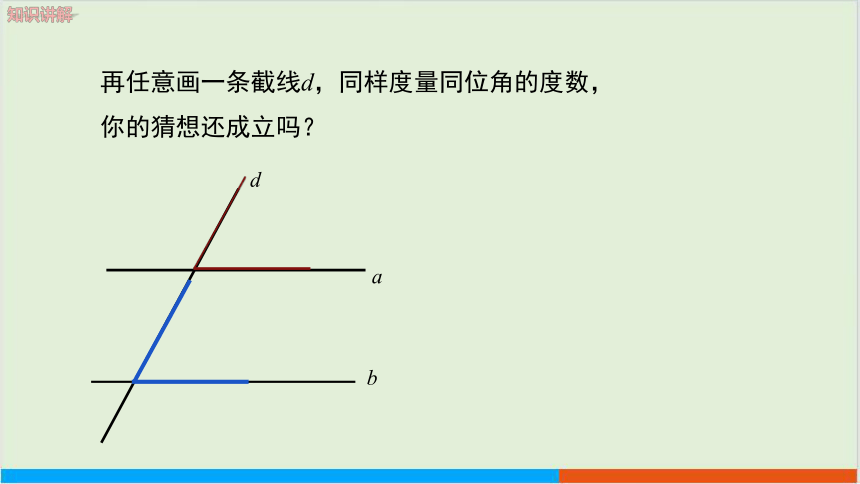
根据这些操作,你能猜想出什么结论?
a
b
d
再任意画一条截线d,同样度量同位角的度数,你的猜想还成立吗?
如图,已知a//b,那么 2与 3相等吗?为什么
b
1
2
a
c
3
解 :∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
平行线的性质2:两条平行直线被第三条直线所截,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等).
∵a∥b(已知),
应用格式:
简单说成:两直线平行,内错角相等.
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a//b (已知),
∴ 1= 2
(两直线平行,同位角相等).
∵ 1+ 4=180°
(邻补角的性质),
∴ 2+ 4=180°
(等量代换).
思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
平行线的性质3:两条平行直线被第三条直线所截,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补).
∵a∥b(已知),
应用格式:
简单说成:两直线平行,同旁内角互补.
解 因为AB∥CD,
所以∠1=∠2= 100°(两直线平行,同位角相等).
又因为∠2 +∠3 = 180°,
所以∠3 = 180°-∠2 = 180°- 100°= 80°.
例1 如图,直线AB,CD被直线EF所截,
AB∥CD,∠1=100°,试求∠3的度数.
解 因为AD∥BC,
所以∠A +∠B = 180°,
∠D+∠C=180°(两直线平行,同旁内角互补).
又因为∠B =∠D (已知),
所以∠A =∠C.
例2 如图,AD∥BC, ∠B = ∠D,试问
∠A与∠C相等吗?为什么?
随堂训练
1.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180°
D.∠3+∠4=180°
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14° B.15°
C.16° D.17°
D
C
3.如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于 ( )
A.36° B.54° C.72° D.108°
B
解析:因为AB∥CD(已知),
所以∠EFG+∠BEF=180°(两直线平行,同旁内角互补),
∠BEG=∠EGF(两直线平行,内错角相等).
因为∠EFG=72°,
所以∠BEF=180°-∠EFG = 180°- 72°= 108°.
又因为GE是∠BEF的平分线,
所以
所以∠EGF=54°.
故应选择B.
4.如图,AB∥CD,若ABE=120°,∠DCE=35°,则∠BEC=
度.
95
解析:过点E作EF∥AB,
则∠ABE+∠BEF=180°(两直线平行,同旁内角互补).
因为∠ABE=120°,
所以∠BEF = 180°- 120°= 60°.
因为AB∥CD,
所以EF∥CD(平行于同一条直线的两条直线平行).
所以∠FEC=∠DCE=35°(两直线平行,内错角相等).
因此∠BEC=∠BEF+∠FEC = 60°+ 35°= 95°.
5. 如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠CED的度数为 .
6.如图,直线 a ∥ b,直线b垂直于直线c,那么直线a垂直于直线c吗
a
b
c
解:a⊥c .
因为两直线平行, 同位角相等.
60°
7.如图,已知平行线AB、CD被直线AE所截.
(1)从 ∠1=110o可以知道∠2 是多少度吗,为什么?
(2)从∠1=110o可以知道 ∠3是多少度吗,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度吗,为什么?
2
3
E
1
4
A
B
D
C
解:(1)∠2=110o
∵两直线平行,内错角相等;
(2)∠3=110o
∵两直线平行, 同位角相等;
(3)∠4=70o
∵两直线平行,同旁内角互补.
8.如图,AB∥CD,DE⊥AC,垂足为点E,∠A=105°,求∠D的度数.
解:∵AB∥CD,
∴∠A+∠C=180°(两直线平行,同旁内角互补).
∵∠A=105°,
∴∠C=180°-105°=75°.
又∵DE⊥AC,
∴∠DEC=90°,
∴∠C+∠D=90°.
∴∠D=90°-75°=15°.
9. 如图,直线AB,CD被直线AE 所截,AB∥CD,
∠1=105°. 求∠2,∠3,∠4的度数.
答:∠2=∠1= 105°,
∠3=180°-∠ 2=75°,
∠4=∠1=105°.
10.如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:因为梯形上、下底互相平行,
根据“两直线平行,同旁内角互补”
可得∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°,
∠C= 180 °-∠B=180°-115°=65°.
课堂小结
同位角相等
内错角相等
同旁内角互补
直线的位置关系
角的数量关系
性质
两直线平行
平行线的性质
第 4 章 相交线与平行线
4.3 平行线的性质
学习目标
1.掌握平行线的性质,会运用平行线的性质判
断角相等或互补;(重点)
2.能够根据平行线的性质进行简单的推理. (难点)
做一做
∠α ∠β; ∠1 ∠2.
图4-20
=
=
在图4-20和图4-21中,AB∥CD,用量角器量下面两个图形中标出的角,然后填空:
73°
73°
60°
60°
图4-21
知识讲解
平行线的性质1:两条平行直线被第三条直线所截,
同位角___.
相等
b
1
2
a
c
5
6
7
8
3
4
简单说成:两直线平行,同位角相等.
∴∠1=∠5 (两直线平行,同位角相等).
∵a∥b(已知),
应用格式:
根据这些操作,你能猜想出什么结论?
a
b
d
再任意画一条截线d,同样度量同位角的度数,你的猜想还成立吗?
如图,已知a//b,那么 2与 3相等吗?为什么
b
1
2
a
c
3
解 :∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
平行线的性质2:两条平行直线被第三条直线所截,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等).
∵a∥b(已知),
应用格式:
简单说成:两直线平行,内错角相等.
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a//b (已知),
∴ 1= 2
(两直线平行,同位角相等).
∵ 1+ 4=180°
(邻补角的性质),
∴ 2+ 4=180°
(等量代换).
思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
平行线的性质3:两条平行直线被第三条直线所截,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补).
∵a∥b(已知),
应用格式:
简单说成:两直线平行,同旁内角互补.
解 因为AB∥CD,
所以∠1=∠2= 100°(两直线平行,同位角相等).
又因为∠2 +∠3 = 180°,
所以∠3 = 180°-∠2 = 180°- 100°= 80°.
例1 如图,直线AB,CD被直线EF所截,
AB∥CD,∠1=100°,试求∠3的度数.
解 因为AD∥BC,
所以∠A +∠B = 180°,
∠D+∠C=180°(两直线平行,同旁内角互补).
又因为∠B =∠D (已知),
所以∠A =∠C.
例2 如图,AD∥BC, ∠B = ∠D,试问
∠A与∠C相等吗?为什么?
随堂训练
1.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180°
D.∠3+∠4=180°
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14° B.15°
C.16° D.17°
D
C
3.如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于 ( )
A.36° B.54° C.72° D.108°
B
解析:因为AB∥CD(已知),
所以∠EFG+∠BEF=180°(两直线平行,同旁内角互补),
∠BEG=∠EGF(两直线平行,内错角相等).
因为∠EFG=72°,
所以∠BEF=180°-∠EFG = 180°- 72°= 108°.
又因为GE是∠BEF的平分线,
所以
所以∠EGF=54°.
故应选择B.
4.如图,AB∥CD,若ABE=120°,∠DCE=35°,则∠BEC=
度.
95
解析:过点E作EF∥AB,
则∠ABE+∠BEF=180°(两直线平行,同旁内角互补).
因为∠ABE=120°,
所以∠BEF = 180°- 120°= 60°.
因为AB∥CD,
所以EF∥CD(平行于同一条直线的两条直线平行).
所以∠FEC=∠DCE=35°(两直线平行,内错角相等).
因此∠BEC=∠BEF+∠FEC = 60°+ 35°= 95°.
5. 如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠CED的度数为 .
6.如图,直线 a ∥ b,直线b垂直于直线c,那么直线a垂直于直线c吗
a
b
c
解:a⊥c .
因为两直线平行, 同位角相等.
60°
7.如图,已知平行线AB、CD被直线AE所截.
(1)从 ∠1=110o可以知道∠2 是多少度吗,为什么?
(2)从∠1=110o可以知道 ∠3是多少度吗,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度吗,为什么?
2
3
E
1
4
A
B
D
C
解:(1)∠2=110o
∵两直线平行,内错角相等;
(2)∠3=110o
∵两直线平行, 同位角相等;
(3)∠4=70o
∵两直线平行,同旁内角互补.
8.如图,AB∥CD,DE⊥AC,垂足为点E,∠A=105°,求∠D的度数.
解:∵AB∥CD,
∴∠A+∠C=180°(两直线平行,同旁内角互补).
∵∠A=105°,
∴∠C=180°-105°=75°.
又∵DE⊥AC,
∴∠DEC=90°,
∴∠C+∠D=90°.
∴∠D=90°-75°=15°.
9. 如图,直线AB,CD被直线AE 所截,AB∥CD,
∠1=105°. 求∠2,∠3,∠4的度数.
答:∠2=∠1= 105°,
∠3=180°-∠ 2=75°,
∠4=∠1=105°.
10.如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:因为梯形上、下底互相平行,
根据“两直线平行,同旁内角互补”
可得∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°,
∠C= 180 °-∠B=180°-115°=65°.
课堂小结
同位角相等
内错角相等
同旁内角互补
直线的位置关系
角的数量关系
性质
两直线平行
平行线的性质
