教学课件:七下·湘教4.4平行线的判定(第二课时 )
文档属性
| 名称 | 教学课件:七下·湘教4.4平行线的判定(第二课时 ) |

|
|
| 格式 | pptx | ||
| 文件大小 | 529.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:31:07 | ||
图片预览






文档简介
(共18张PPT)
第 4 章 相交线与平行线
4.4 平行线的判定
第2课时 平行线的判定(2)
学习目标
1.进一步掌握推理、证明的基本格式,掌握平行线判定方法2、3的推理过程. (重点)
2.能运用判定方法1、2、3进行简单的推理和解答相关问题.
根据平行线的判定填空.
∵∠1=_____;
∴a//b( ).
3
a
b
c
1
2
4
∠2
同位角相等,两直线平行
旧知回顾
两条直线被第三条直线所截,能否利用内错角来判定两条直线平行呢?
如图,直线 AB,CD被直线EF所截,∠2与∠3是内错角.
1
3
2
A
B
C
D
E
F
已知∠2=∠3,
又∵∠3=∠1(对顶角相等),
∴∠1=∠2.
∴AB∥CD(同位角相等,两直线平行).
知识讲解
平行线的判定方法2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
∵∠3=∠2 (已知),
∴a∥b(内错角相等,两直线平行).
应用格式:
b
1
2
a
c
3
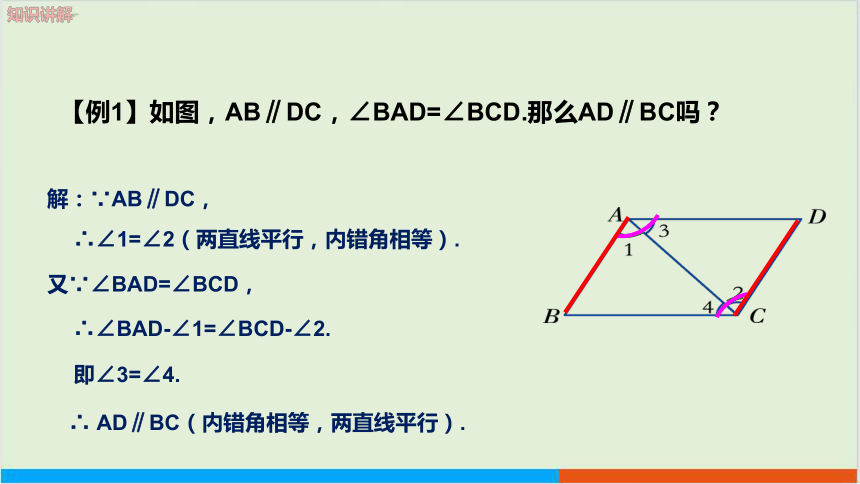
【例1】如图,AB∥DC,∠BAD=∠BCD.那么AD∥BC吗?
解:∵AB∥DC,
∴∠1=∠2(两直线平行,内错角相等).
又∵∠BAD=∠BCD,
∴∠BAD-∠1=∠BCD-∠2.
即∠3=∠4.
∴ AD∥BC(内错角相等,两直线平行).
两条直线被第三条直线所截,能否利用同旁内角来判定两条
直线平行呢?
如图,直线 AB,CD被直线EF所截,∠1与∠2是同旁内角.
∵∠1+∠2= 180o(已知),
且∠2+∠3= 180o,
∴∠3=∠1.
∴AB∥CD(同位角相等,两直线平行).
1
3
2
A
B
C
D
E
F
平行线的判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
∵∠4+∠2=180° (已知),
∴a∥b(同旁内角互补,两直线平行).
应用格式:
b
1
2
a
c
4
解:∵AD∥BC,
∴∠1+∠3=180°.(两直线平行,同旁内角互补),
∴ AB∥DC(同旁内角互补,两直线平行).
【例2】如图,∠1=∠2= 50°,AD∥BC,那么 AB∥DC吗?
则∠3=180°-∠1=180°-50°=130°,
∴∠2+∠3=50°+130°=180°,
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的性质与判定关系:
平行线的三个判定方法:
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
小结
练一练 如图,点A在直线l上,如果∠B= 75°,∠C= 43° ,则
(1)当 ∠1= 时,直线l ∥BC;
(2)当 ∠2= 时,直线l ∥BC.
75°
43°
1
2
l
A
B
C
75°
43°
内错角相等,两条直线平行.
① ∵ ∠1 =_____(已知),
∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),
∴ CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知),
∴ _____∥_____( ).
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知),
∴ CE∥AB( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
例 3 根据条件完成填空.
随堂训练
1.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠4=180°,则a∥c
C
2.如图,已知∠1=30°,∠2或∠3满足条件
,则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
3.如图,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;⑤∠B=∠D.其中,一定能判定AB∥CD的条件有 (填写所有正确的序号).
①③④
4.如图,已知BC平分∠ACD,且∠1=∠2,AB与CD平行吗?为什么?
解:AB∥CD.理由如下:
∵BC平分∠ACD,
∴∠1=∠BCD.
∵∠1=∠2,
∴∠2=∠BCD,
∴AB∥CD(内错角相等,两直线平行).
5.如图,∠ADE=∠DEF, ∠EFC+∠C=180°, 试问AD与 BC平行吗?为什么?
A
B
C
D
E
F
解:∵∠ADE=∠DEF,
∴AD∥EF (内错角相等,两直线平行).
∵∠EFC+∠C = 180°,
∴BC∥EF (同旁内角互补,两直线平行).
∴AD∥BC.
课堂小结
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴a∥b
相等, 两直线平行 ∵ (已知), ∴a∥b 互补, 两直线平行 ∵ (已知), ∴a∥b 判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
第 4 章 相交线与平行线
4.4 平行线的判定
第2课时 平行线的判定(2)
学习目标
1.进一步掌握推理、证明的基本格式,掌握平行线判定方法2、3的推理过程. (重点)
2.能运用判定方法1、2、3进行简单的推理和解答相关问题.
根据平行线的判定填空.
∵∠1=_____;
∴a//b( ).
3
a
b
c
1
2
4
∠2
同位角相等,两直线平行
旧知回顾
两条直线被第三条直线所截,能否利用内错角来判定两条直线平行呢?
如图,直线 AB,CD被直线EF所截,∠2与∠3是内错角.
1
3
2
A
B
C
D
E
F
已知∠2=∠3,
又∵∠3=∠1(对顶角相等),
∴∠1=∠2.
∴AB∥CD(同位角相等,两直线平行).
知识讲解
平行线的判定方法2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
∵∠3=∠2 (已知),
∴a∥b(内错角相等,两直线平行).
应用格式:
b
1
2
a
c
3
【例1】如图,AB∥DC,∠BAD=∠BCD.那么AD∥BC吗?
解:∵AB∥DC,
∴∠1=∠2(两直线平行,内错角相等).
又∵∠BAD=∠BCD,
∴∠BAD-∠1=∠BCD-∠2.
即∠3=∠4.
∴ AD∥BC(内错角相等,两直线平行).
两条直线被第三条直线所截,能否利用同旁内角来判定两条
直线平行呢?
如图,直线 AB,CD被直线EF所截,∠1与∠2是同旁内角.
∵∠1+∠2= 180o(已知),
且∠2+∠3= 180o,
∴∠3=∠1.
∴AB∥CD(同位角相等,两直线平行).
1
3
2
A
B
C
D
E
F
平行线的判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
∵∠4+∠2=180° (已知),
∴a∥b(同旁内角互补,两直线平行).
应用格式:
b
1
2
a
c
4
解:∵AD∥BC,
∴∠1+∠3=180°.(两直线平行,同旁内角互补),
∴ AB∥DC(同旁内角互补,两直线平行).
【例2】如图,∠1=∠2= 50°,AD∥BC,那么 AB∥DC吗?
则∠3=180°-∠1=180°-50°=130°,
∴∠2+∠3=50°+130°=180°,
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的性质与判定关系:
平行线的三个判定方法:
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
小结
练一练 如图,点A在直线l上,如果∠B= 75°,∠C= 43° ,则
(1)当 ∠1= 时,直线l ∥BC;
(2)当 ∠2= 时,直线l ∥BC.
75°
43°
1
2
l
A
B
C
75°
43°
内错角相等,两条直线平行.
① ∵ ∠1 =_____(已知),
∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),
∴ CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知),
∴ _____∥_____( ).
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知),
∴ CE∥AB( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
例 3 根据条件完成填空.
随堂训练
1.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠4=180°,则a∥c
C
2.如图,已知∠1=30°,∠2或∠3满足条件
,则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
3.如图,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;⑤∠B=∠D.其中,一定能判定AB∥CD的条件有 (填写所有正确的序号).
①③④
4.如图,已知BC平分∠ACD,且∠1=∠2,AB与CD平行吗?为什么?
解:AB∥CD.理由如下:
∵BC平分∠ACD,
∴∠1=∠BCD.
∵∠1=∠2,
∴∠2=∠BCD,
∴AB∥CD(内错角相等,两直线平行).
5.如图,∠ADE=∠DEF, ∠EFC+∠C=180°, 试问AD与 BC平行吗?为什么?
A
B
C
D
E
F
解:∵∠ADE=∠DEF,
∴AD∥EF (内错角相等,两直线平行).
∵∠EFC+∠C = 180°,
∴BC∥EF (同旁内角互补,两直线平行).
∴AD∥BC.
课堂小结
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴a∥b
相等, 两直线平行 ∵ (已知), ∴a∥b 互补, 两直线平行 ∵ (已知), ∴a∥b 判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
