教学课件:七下·湘教4.5垂线(第一课时 垂线与垂直)
文档属性
| 名称 | 教学课件:七下·湘教4.5垂线(第一课时 垂线与垂直) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:31:07 | ||
图片预览






文档简介
(共21张PPT)
第4章 相交线与平行线
4.5 垂 线
第一课时 垂线与垂直
学习目标
1.理解垂线的有关概念、性质;(重点)
2. 会应用垂线的性质解决简单的问题. (重点、难点)
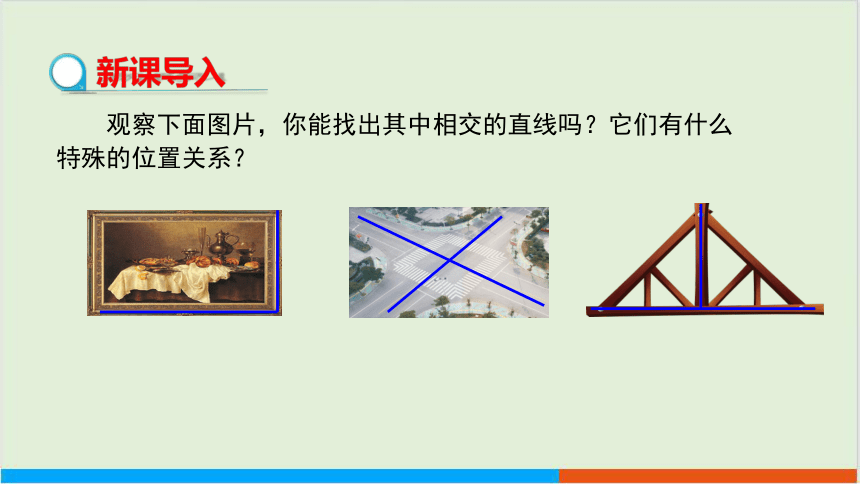
新课导入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
知识讲解
在相交线的模型中,固定木条a,转动木条b,当b的
位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
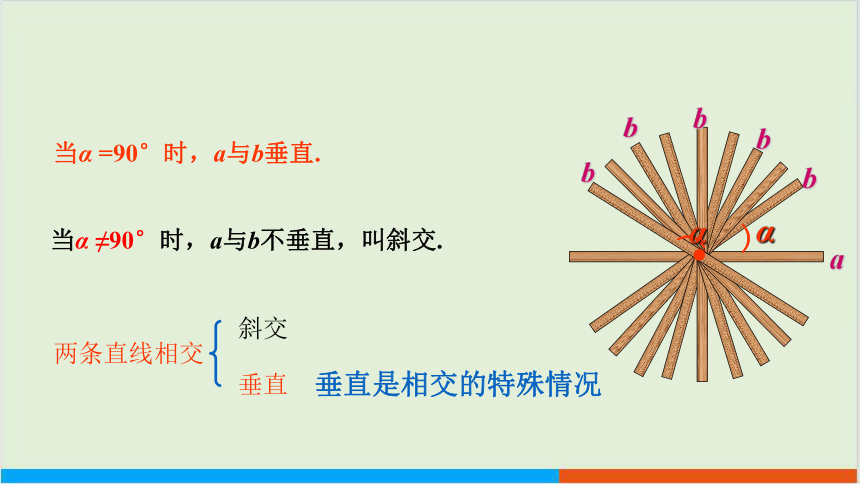
当α =90°时,a与b垂直.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
当两条直线相交所成的四个角中,有一个角是直角(90度)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
b
a
O
1.垂直、垂线的定义
“⊥”
垂直符号:
例如:如图,a、b互相垂直, 垂足为O,则记为:
a⊥b或b⊥a.
若要强调垂足,则记为:a⊥b, 垂足为O.
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线.
读做“a垂直于b”或“b垂直于a”
斜线定义:两条直线相交不成直角时,其中一条直线叫做另一条直线的斜线,它们的交点叫做斜足.
如图,直线CD是AB的斜线,同样,直线AB也是CD的斜线,点O是斜足.
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
你能再举出其他例子吗?
生活中的垂直
如图,在同一平面内,如果直线a⊥l, b⊥l,那么a//b吗?
l
a
b
1
2
【解析】a∥b.因为∠1=∠2=90°,
它们是同位角,所以a//b.
2.垂线性质1
在同一平面内,垂直于同一条直线的两条直线平行.
如图,在同一平面内,如果a//b,l⊥a,那么l⊥b吗?
l
a
b
1
2
【解析】l⊥b.因为l⊥a,
所以∠1=90°,
因为a//b,所以∠2=∠1=90°,
从而l⊥b.
在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条.
3.垂线性质2
【例1】 在如图所示的简易屋架中,BD,AE,HF都垂直于CG,若∠1=60°,求∠2的度数.
解:因为BD,AE都垂直于CG,
所以 BD∥AE(在平面内,垂直于同一条直线的两条直线平行).
从而 ∠2=∠1=60°(两直线平行,同位角相等).
【例2】 如图,已知CD⊥AB,∠1=∠2,求∠BFE的度数.
解:因为∠1=∠2,
所以EF∥CD(同位角相等,两直线平行).
又因为CD⊥AB,所以 EF⊥AB
(一直线若垂直于两平行线中的一条,必垂直于另一条),
即∠BFE=∠BDC=90°.
B
【归纳总结】垂直定义的应用
(1)由两直线垂直可得其夹角为90°;
(2)由两直线的夹角为90°,可得两直线互相垂直.
随堂训练
B
B
4. (1)如图1,若直线a、b相交于点O,∠1=90°,
则 ;
(2)若直线AB、CD相交于点O,且AB⊥CD,则
∠BOD =______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比
为1∶3,那么∠COA=____ ,∠BOC的补角
为 .
O
a
b
1
B
C
A
O
a⊥b
90°
60°
150°
图1
图2
垂直
7.如图,直线AB,CD相交于点O,EO⊥CD, ∠BOE=60°,求∠AOC的度数.
A
B
C
D
E
O
解:因为 EO⊥CD,
所以∠EOD=90°.
又∠BOE+∠BOD=∠EOD=90°,
所以∠BOD=90°-∠BOE=90°-60°=30°.
又 ∠AOC=∠BOD ,
所以 ∠AOC=30°.
8.如图,AB⊥AD,CD⊥AD,∠B=56°,求∠C.
解: 因为AB⊥AD,
CD⊥AD,
所以DC∥AB.
所以∠B+∠C=180.
所以∠C=180°-∠B=180°-56°=124°.
A
B
C
D
2.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线_______于另一条.
垂线
两条直线相交所成的四个角中,有一个角是 时,这两条直线叫做互相垂直.
直角
垂线的性质
1.在同一平面内,垂直于同一条直线的两条直线 .
平行
垂直
课堂小结
第4章 相交线与平行线
4.5 垂 线
第一课时 垂线与垂直
学习目标
1.理解垂线的有关概念、性质;(重点)
2. 会应用垂线的性质解决简单的问题. (重点、难点)
新课导入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
知识讲解
在相交线的模型中,固定木条a,转动木条b,当b的
位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
当α =90°时,a与b垂直.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
当两条直线相交所成的四个角中,有一个角是直角(90度)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
b
a
O
1.垂直、垂线的定义
“⊥”
垂直符号:
例如:如图,a、b互相垂直, 垂足为O,则记为:
a⊥b或b⊥a.
若要强调垂足,则记为:a⊥b, 垂足为O.
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线.
读做“a垂直于b”或“b垂直于a”
斜线定义:两条直线相交不成直角时,其中一条直线叫做另一条直线的斜线,它们的交点叫做斜足.
如图,直线CD是AB的斜线,同样,直线AB也是CD的斜线,点O是斜足.
日常生活中,两条直线互相垂直的情形很常见,说出图中的一些互相垂直的线条.
你能再举出其他例子吗?
生活中的垂直
如图,在同一平面内,如果直线a⊥l, b⊥l,那么a//b吗?
l
a
b
1
2
【解析】a∥b.因为∠1=∠2=90°,
它们是同位角,所以a//b.
2.垂线性质1
在同一平面内,垂直于同一条直线的两条直线平行.
如图,在同一平面内,如果a//b,l⊥a,那么l⊥b吗?
l
a
b
1
2
【解析】l⊥b.因为l⊥a,
所以∠1=90°,
因为a//b,所以∠2=∠1=90°,
从而l⊥b.
在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条.
3.垂线性质2
【例1】 在如图所示的简易屋架中,BD,AE,HF都垂直于CG,若∠1=60°,求∠2的度数.
解:因为BD,AE都垂直于CG,
所以 BD∥AE(在平面内,垂直于同一条直线的两条直线平行).
从而 ∠2=∠1=60°(两直线平行,同位角相等).
【例2】 如图,已知CD⊥AB,∠1=∠2,求∠BFE的度数.
解:因为∠1=∠2,
所以EF∥CD(同位角相等,两直线平行).
又因为CD⊥AB,所以 EF⊥AB
(一直线若垂直于两平行线中的一条,必垂直于另一条),
即∠BFE=∠BDC=90°.
B
【归纳总结】垂直定义的应用
(1)由两直线垂直可得其夹角为90°;
(2)由两直线的夹角为90°,可得两直线互相垂直.
随堂训练
B
B
4. (1)如图1,若直线a、b相交于点O,∠1=90°,
则 ;
(2)若直线AB、CD相交于点O,且AB⊥CD,则
∠BOD =______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比
为1∶3,那么∠COA=____ ,∠BOC的补角
为 .
O
a
b
1
B
C
A
O
a⊥b
90°
60°
150°
图1
图2
垂直
7.如图,直线AB,CD相交于点O,EO⊥CD, ∠BOE=60°,求∠AOC的度数.
A
B
C
D
E
O
解:因为 EO⊥CD,
所以∠EOD=90°.
又∠BOE+∠BOD=∠EOD=90°,
所以∠BOD=90°-∠BOE=90°-60°=30°.
又 ∠AOC=∠BOD ,
所以 ∠AOC=30°.
8.如图,AB⊥AD,CD⊥AD,∠B=56°,求∠C.
解: 因为AB⊥AD,
CD⊥AD,
所以DC∥AB.
所以∠B+∠C=180.
所以∠C=180°-∠B=180°-56°=124°.
A
B
C
D
2.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线_______于另一条.
垂线
两条直线相交所成的四个角中,有一个角是 时,这两条直线叫做互相垂直.
直角
垂线的性质
1.在同一平面内,垂直于同一条直线的两条直线 .
平行
垂直
课堂小结
