教学课件:七下·湘教4.6 两条平行线间的距离
文档属性
| 名称 | 教学课件:七下·湘教4.6 两条平行线间的距离 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:31:07 | ||
图片预览



文档简介
(共23张PPT)
第 4 章 相交线与平行线
4.6 两条平行线间的距离
1.掌握公垂线段的概念、性质及其意义;
2.会度量或求平行线段的距离. (重点)
学 习 目 标
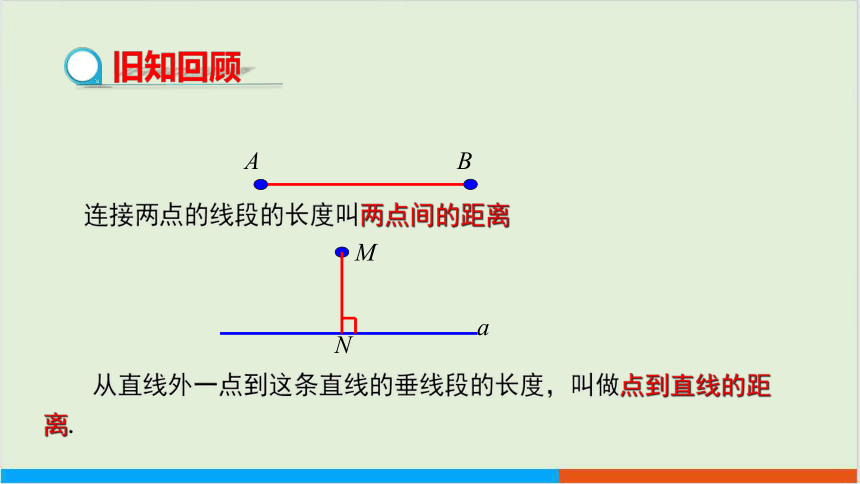
A
B
连接两点的线段的长度叫两点间的距离
M
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
N
a
旧知回顾
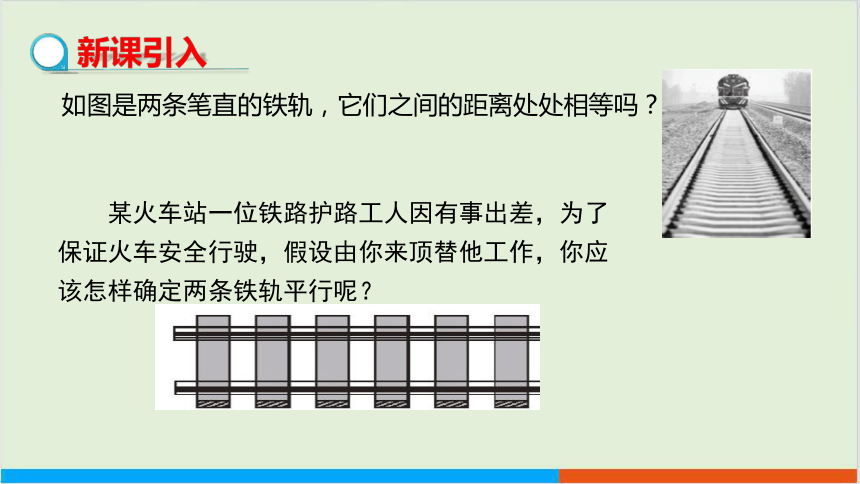
如图是两条笔直的铁轨,它们之间的距离处处相等吗?
某火车站一位铁路护路工人因有事出差,为了保证火车安全行驶,假设由你来顶替他工作,你应该怎样确定两条铁轨平行呢?
新课引入
活动1:请各位同学用直尺量一量自己的数学课本,它的宽度是多少?
你的直尺与课本的两边成什么角度?量在课本的哪个位置?大家量得的结果是一样的吗?
可以把直尺放在课本上任何一个位置,但必须保持直尺与课本的两边互相垂直,量得的结果是一样的.
两条平行线间的距离
知识讲解
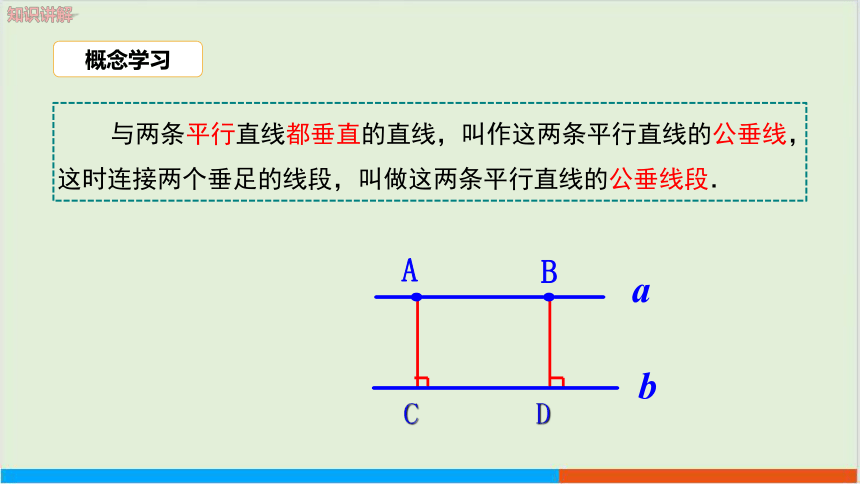
与两条平行直线都垂直的直线,叫作这两条平行直线的公垂线,这时连接两个垂足的线段,叫做这两条平行直线的公垂线段.
概念学习
C
D
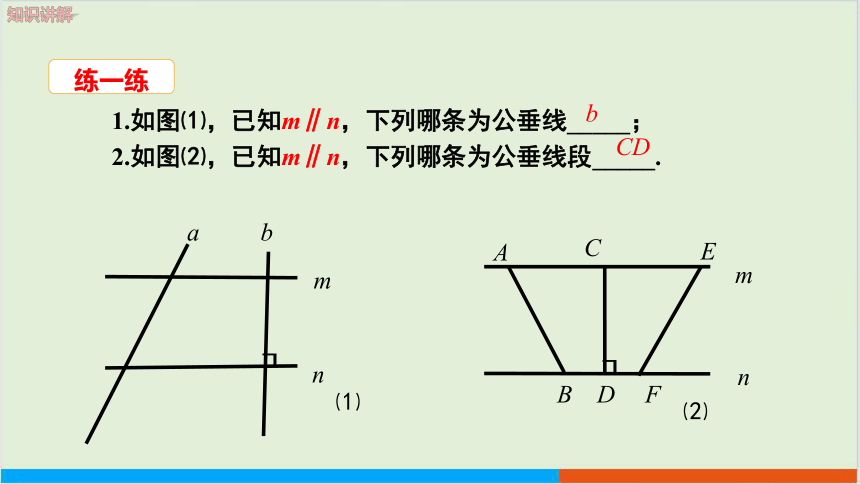
1.如图⑴,已知m∥n,下列哪条为公垂线_____;
2.如图⑵,已知m∥n,下列哪条为公垂线段_____.
m
n
m
n
a
b
A
B
E
C
D
F
┒
┒
b
CD
⑴
⑵
练一练
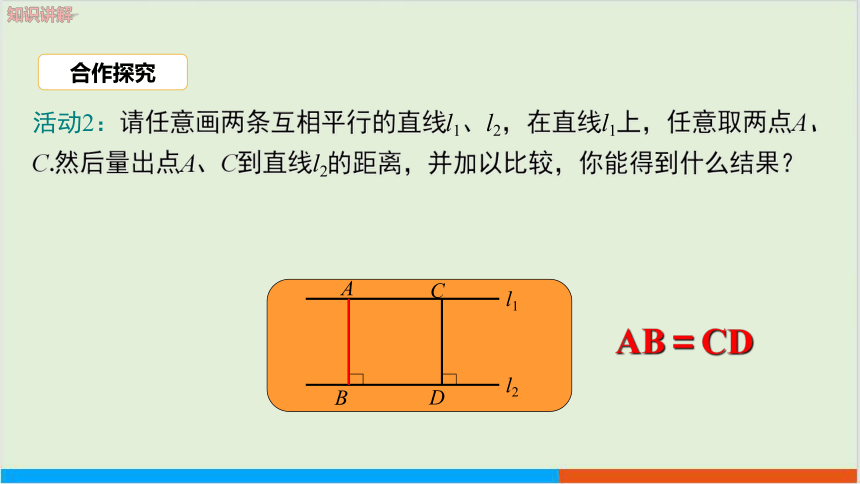
活动2:请任意画两条互相平行的直线l1、l2,在直线l1上,任意取两点A、C.然后量出点A、C到直线l2的距离,并加以比较,你能得到什么结果?
AB=CD
合作探究
A
B
C
D
l1
l2
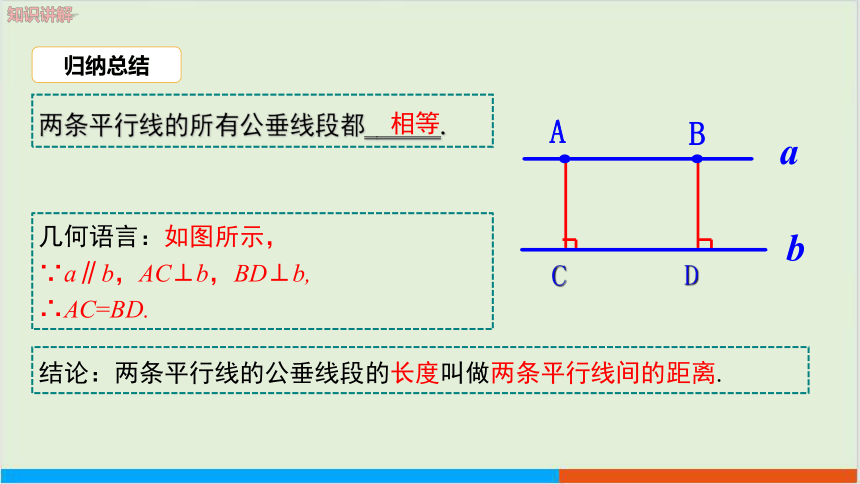
两条平行线的所有公垂线段都 .
相等
几何语言:如图所示,
∵a∥b,AC⊥b,BD⊥b,
∴AC=BD.
C
D
结论:两条平行线的公垂线段的长度叫做两条平行线间的距离.
归纳总结
如图,设l1//l2,A,B分别为l1,l2上的任意点,连接线段AB,再过A作AC⊥l2,垂足为C,则AC是l1,l2之间的公垂线段,AB是l1,l2之间的斜线段.因为AC,AB又分别是A点到l2的垂线段和斜线段,所以AC两平行线上各取一点连接而成的所有线段中,公垂线段最短.
A
B
C
l1
l2
思考:你可以证明这个猜想是否正确吗?
C. 点到点的距离
A.两平行线间的距离
B.点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
跳
远
的
成
绩
C. 点到点的距离
A.两平行线间的距离
B.点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
直跑道间
距离
说一说
如图,平行线AB与CD间的距离与AB上的点P到直线CD的距离有什么关系?
你能用刻度尺度量出平行线AB 与CD之间的距离吗?
平行线AB与CD的距离,也就是AB上任意一点P到直线CD的距离.
我们可以把直线与直线的距离转化为点到直线的距离.
例1 如图,设a,b,c是三条互相平行的直线.已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离.
在a上任取一点A,过A作AC⊥a,分别与b,c相交于B,C两点,
AC=AB+BC=5+2=7.
A
b
c
B
C
a
5厘米
2厘米
解:
因此a与c的距离是7厘米.
典例精析
则AB,BC,AC分别表示a与b,b与c,
a与c的公垂线段.
(1)如图1,
∵AB=5cm, BC=2cm,
∴AC=7cm.
A
B
C
变式:设a、b、c是三条互相平行的直线,已知a与b的距离为5cm,b与c 的距离为2cm,求a与c的距离.
解:有两种情况
图1
a
b
c
a
c
b
A
B
C
图2
(2)如图2 ,
∵AB=5cm, BC=2cm, ∴AC=3cm.
例2:如图,已知AD//BC,判断 与 是否相等,并说明理由.
解:∵AD∥BC,
∴△ABC与△DBC的高相等.
∵ △ABC与△DBC的底都是BC,
∴ △AB C与△DBC同底 等高,
∴S△A BC=S△DBC.
练一练:如图,CD//AB,P,Q为直线CD上的任意两点,三角形PAB和三角形QAB的面积有什么关系?为什么?
△PAB与△QAB面积相等.
∵ CD∥AB,
∴ PM⊥AB ,QN⊥AB,
∴ PM=QN.
∴ S△PAB=S△QAB.
解:
A
B
C
D
Q
P
M
N
2.点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5cm,则点M到AB的距离为( )
A.大于5 cm B.小于5 cm
C.5 cm D.不确定
1.两平行线的公垂线段有多少条?( )
A.1 B.2
C.无数条 D.一条也没有
C
C
随堂练习
3.如图,a⊥c,b⊥c,c交a,b于A、B两点,d交AB于C、D两点,且d与c不平行,则AB CD(填“>”、“=”、“<”)
(第3题图)
4.如图,长方形ABCD的宽AD的长度是2cm,点P到AB的距离是1.6cm,那么点P到CD的距离是
(第4题图)
<
3.6cm
.
6.已知a∥b∥c,a与b之间的距离为3cm,b与c之间的距离为4cm,则a与c之间的距离为 cm.
5.如图,已知直线MN∥PQ,BC=4cm,若三角形ABC的面积为6cm ,则平行线MN,PQ的距离是 cm.
3
7或1
如图1,MN∥AB, P、Q为直线MN上的任意两点,ΔPAB和ΔQAB的面积相等吗?为什么?M P Q N2.如图2,MN∥AB, P是MN上的一动点,P沿MN的方向每次移动1cm,当它移动10cm时得到ΔP1AB,那么ΔP1AB的面积是多少?AB图1M P NP1A B图2 acm2拓展提升相等acm2两条平行线的距离
概念
性质
公垂线,
公垂线段,
平行线间的距离
两条平行线的公垂线段都相等
课堂小结
第 4 章 相交线与平行线
4.6 两条平行线间的距离
1.掌握公垂线段的概念、性质及其意义;
2.会度量或求平行线段的距离. (重点)
学 习 目 标
A
B
连接两点的线段的长度叫两点间的距离
M
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
N
a
旧知回顾
如图是两条笔直的铁轨,它们之间的距离处处相等吗?
某火车站一位铁路护路工人因有事出差,为了保证火车安全行驶,假设由你来顶替他工作,你应该怎样确定两条铁轨平行呢?
新课引入
活动1:请各位同学用直尺量一量自己的数学课本,它的宽度是多少?
你的直尺与课本的两边成什么角度?量在课本的哪个位置?大家量得的结果是一样的吗?
可以把直尺放在课本上任何一个位置,但必须保持直尺与课本的两边互相垂直,量得的结果是一样的.
两条平行线间的距离
知识讲解
与两条平行直线都垂直的直线,叫作这两条平行直线的公垂线,这时连接两个垂足的线段,叫做这两条平行直线的公垂线段.
概念学习
C
D
1.如图⑴,已知m∥n,下列哪条为公垂线_____;
2.如图⑵,已知m∥n,下列哪条为公垂线段_____.
m
n
m
n
a
b
A
B
E
C
D
F
┒
┒
b
CD
⑴
⑵
练一练
活动2:请任意画两条互相平行的直线l1、l2,在直线l1上,任意取两点A、C.然后量出点A、C到直线l2的距离,并加以比较,你能得到什么结果?
AB=CD
合作探究
A
B
C
D
l1
l2
两条平行线的所有公垂线段都 .
相等
几何语言:如图所示,
∵a∥b,AC⊥b,BD⊥b,
∴AC=BD.
C
D
结论:两条平行线的公垂线段的长度叫做两条平行线间的距离.
归纳总结
如图,设l1//l2,A,B分别为l1,l2上的任意点,连接线段AB,再过A作AC⊥l2,垂足为C,则AC是l1,l2之间的公垂线段,AB是l1,l2之间的斜线段.因为AC,AB又分别是A点到l2的垂线段和斜线段,所以AC
A
B
C
l1
l2
思考:你可以证明这个猜想是否正确吗?
C. 点到点的距离
A.两平行线间的距离
B.点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
跳
远
的
成
绩
C. 点到点的距离
A.两平行线间的距离
B.点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
直跑道间
距离
说一说
如图,平行线AB与CD间的距离与AB上的点P到直线CD的距离有什么关系?
你能用刻度尺度量出平行线AB 与CD之间的距离吗?
平行线AB与CD的距离,也就是AB上任意一点P到直线CD的距离.
我们可以把直线与直线的距离转化为点到直线的距离.
例1 如图,设a,b,c是三条互相平行的直线.已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离.
在a上任取一点A,过A作AC⊥a,分别与b,c相交于B,C两点,
AC=AB+BC=5+2=7.
A
b
c
B
C
a
5厘米
2厘米
解:
因此a与c的距离是7厘米.
典例精析
则AB,BC,AC分别表示a与b,b与c,
a与c的公垂线段.
(1)如图1,
∵AB=5cm, BC=2cm,
∴AC=7cm.
A
B
C
变式:设a、b、c是三条互相平行的直线,已知a与b的距离为5cm,b与c 的距离为2cm,求a与c的距离.
解:有两种情况
图1
a
b
c
a
c
b
A
B
C
图2
(2)如图2 ,
∵AB=5cm, BC=2cm, ∴AC=3cm.
例2:如图,已知AD//BC,判断 与 是否相等,并说明理由.
解:∵AD∥BC,
∴△ABC与△DBC的高相等.
∵ △ABC与△DBC的底都是BC,
∴ △AB C与△DBC同底 等高,
∴S△A BC=S△DBC.
练一练:如图,CD//AB,P,Q为直线CD上的任意两点,三角形PAB和三角形QAB的面积有什么关系?为什么?
△PAB与△QAB面积相等.
∵ CD∥AB,
∴ PM⊥AB ,QN⊥AB,
∴ PM=QN.
∴ S△PAB=S△QAB.
解:
A
B
C
D
Q
P
M
N
2.点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5cm,则点M到AB的距离为( )
A.大于5 cm B.小于5 cm
C.5 cm D.不确定
1.两平行线的公垂线段有多少条?( )
A.1 B.2
C.无数条 D.一条也没有
C
C
随堂练习
3.如图,a⊥c,b⊥c,c交a,b于A、B两点,d交AB于C、D两点,且d与c不平行,则AB CD(填“>”、“=”、“<”)
(第3题图)
4.如图,长方形ABCD的宽AD的长度是2cm,点P到AB的距离是1.6cm,那么点P到CD的距离是
(第4题图)
<
3.6cm
.
6.已知a∥b∥c,a与b之间的距离为3cm,b与c之间的距离为4cm,则a与c之间的距离为 cm.
5.如图,已知直线MN∥PQ,BC=4cm,若三角形ABC的面积为6cm ,则平行线MN,PQ的距离是 cm.
3
7或1
如图1,MN∥AB, P、Q为直线MN上的任意两点,ΔPAB和ΔQAB的面积相等吗?为什么?M P Q N2.如图2,MN∥AB, P是MN上的一动点,P沿MN的方向每次移动1cm,当它移动10cm时得到ΔP1AB,那么ΔP1AB的面积是多少?AB图1M P NP1A B图2 acm2拓展提升相等acm2两条平行线的距离
概念
性质
公垂线,
公垂线段,
平行线间的距离
两条平行线的公垂线段都相等
课堂小结
