教学课件:七下·湘教6.1.3 众数
图片预览








文档简介
(共26张PPT)
第6章 数据的分析
6.1.3 众数
第6章 数据的分析
6.1 平均数、中位数、众数
学 习 目 标
1
理解众数的概念,会求一组数据的众数;(重点)
2
掌握众数的作用,会用众数分析实际问题. (难点)
了解平均数、中位数、众数各自的特点,能选择适当的量反映数据的集中趋势.(难点)
3
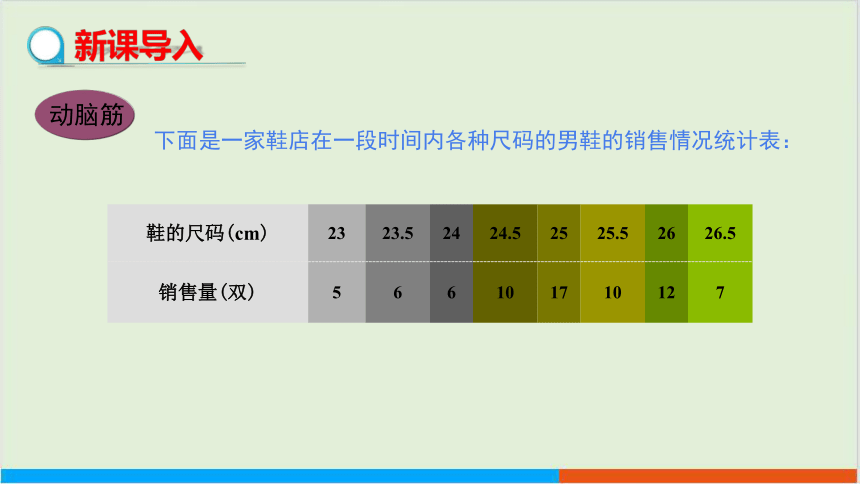
动脑筋
下面是一家鞋店在一段时间内各种尺码的男鞋的销售情况统计表:
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 10 17 10 12 7
新课导入
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 10 17 10 12 7
这家店销售量最多的男鞋是哪种尺码的?店主最关心的问题是什么?
这家店销售量最多的是25cm的鞋,店主最关心的就是销售量,所以店主下次进货时可以多进这个尺码的鞋.
在上面的问题中,25是鞋的尺码中出现次数最多的数,所以25是这组数据的众数.
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 10 17 10 12 7
1.众数
在一组数据中,把出现次数最多的数叫做这组数据的众数.
当一组数据中某数据多次重复出现时,常可以用众数作为这组数据的数值的一个代表值.
一组数据的众数可以不止一个.
知识讲解
下表是某学习小组一次数学测验的成绩统计表:
已知该小组本次数学测验的平均分是85分,则测验成绩的众数是( )
A.80 分 B.85 分 C.90 分 D.80 分和90 分
解析:要确定众数,必须先确定x,
由平均数的概念可知70×1+80×3+90x+100×1 = 85(1+3+x+1),即410+90x = 425+85x,解得x = 3.
从而可知这组数据中80 和90 出现的次数最多,都是3 次,故众数有两个,80 分和90 分.
D
例1
注意:
(1)一组数据的众数一定出现在这组数据中.
(2)一组数据的众数可能不止一个.如1,1,2,3,3,
5中众数是1和3.
(3)众数是一组数据中出现次数最多的数据而不是数据出现的次数,如1,1,1,2,2,5中众数是1而不是3.
(4) 众数的单位与原数据的单位一致.
当数据组中数据重复出现的情况并不突出时,讨论众数
是没有意义的.
某公司全体职工的月工资如下:
试求出该公司工资数据中的众数、中位数和平均数.
月工资(元) 18000 12000 8000 6000 4000 2500 2000 1500 1200
人数 1 (总经理) 2 (副总经理) 3 4 10 20 22 12 6
2.平均数、中位数和众数的选择
例2
解: 在上述80个数据中,2000出现了22次,出现的
次数最多,因此这组数据的众数是2000.
出现次数最多的数
月工资(元) 18000 12000 8000 6000 4000 2500 2000 1500 1200
人数 1 (总经理) 2 (副总经理) 3 4 10 20 22 12 6
把这80个数据按从小到大的顺序排列后,可以
发现位于中间的数是2000,2500,因此这组数
据的中位数是
这组数据的平均数为
我们把这组数据的众数、中位数、平均数表示在图中:
议一议
在例2中,你认为用平均数、中位数或众数中的哪一个更能反映该公司的工资水平?
工资的平均数3115 偏高,因为大多数员工的工资都达不到这个平均数,用它来作为该公司员工工资的代表值并不合适.
众数是2000,中位数是2250,它们代表了大多数人的工资水平,不偏高也不偏低,较能反映工资水平的实际情况.
公司总经理最关心的是公司月工资的总额,所以他关注的是平均数.
普通员工关注的是自己的收入在本公司职工群体中的位置,中位数能帮助职工了解自己的工资收入是“中上”还是“中下”水平……
在例2中,对于职工月工资数据的平均数、中位数和众数,你认为该公司总经理、普通员工及应聘者将分别关注哪一个?说说你的理由, 并相互交流.
应聘者关注的是该公司月工资的众数,因为应聘者最想知道的是公司发给大多数员工的工资数,这也是一般的应聘者将会拿到的工资.
说一说
平均数、中位数和众数都是一组数据的代表,它们从不同侧面反映了数据的集中趋势.
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息,因此在现实生活中应用较广,但它容易受极端值的影响;
中位数对极端值不敏感,但没有利用数据中所有的信息;
众数只能反映一组数据中出现次数最多的数据,也没有利用数据中所有的信息.
归纳:平均数、众数和中位数这三个统计量各自的特点
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息.
归纳:平均数、众数和中位数这三个统计量各自的优点
众数是当一组数据中某一数据多次重复出现时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势;
中位数的计算很少,仅与数据的排列位置有关,不易受极端值影响,中位数可能出现在所给数据中,也可能不在所给数据中.
公园有甲、乙两队游客在做团体游戏,两队游客的年龄(单位:岁)如下:
例3
(1)分别算出两队游客年龄的平均数、众数和中位数.
(2)甲、乙两队游客年龄的平均数能代表他们各自的年龄特征吗?如果不能,哪个数据能代表?
分析:(1)将两组数据分别代入平均数的计算公式计算;根据中位数和众数的定义来分别确定甲、乙两队的中位数和众数.
(2)要判断平均数能否代表各组年龄的特征,就是要看平均数是否与各组数据反映的实际意义相吻合.
(2)甲队游客年龄的平均数能代表他们的年龄特征,乙队游客年龄的平均数不能代表他们的年龄特征.
对于乙队游客而言,10 人中有8 人的年龄在9 岁以下,而说他们的平均年龄是15 岁,会让人误认为这队游客的年龄都在15 岁左右,所以乙队的平均数不能代表该队游客年龄的特征. 可选用中位数或众数来代表乙队游客的年龄特征.
1.要调查多数同学们喜欢看的电视节目,应关注的是( )
A.平均数 B.中位数 C.众数
2.数据1,2, 8,5,3,9,5,4,5,4的众数分别为 .
C
随堂训练
5
3.下面的扇形图描述了某种运动服的S号、M号、L号、XL号、XXL号在一家商场的销售情况.请你为这家商场提出进货建议.
S
16%
8%
24%
30%
22%
M
L
XL
XXL
解:因为众数是M号,所以建议商场多进M号的运动服,其次是进S号,再其次进L号,少进XXL号的运动服.
4. 某校抽取八年级某班50名学生,调查他们一周做
家务所用时间,得到一组数据,并绘制成下表,请根
据下表完成各题:
每周做家务的时间(小时) 0 1 1.5 2 2.5 3 3.5 4
人数 2 2 6 12 13 4 3
(1)填写表格中未完成的部分;
(2)该班学生每周做家务的平均时间是 .
2.44
(3)这组数据的中位数是 ,众数是 .
2.5
3
8
5.某校男子足球队的年龄分布如下面的条形图所示.
请找出这些队员年龄的平均数、众数、中位数,
并解释它们的意义.
人数
13
14
15
16
17
18
年龄/岁
0
2
4
6
8
10
解:这些队员年龄的平均数为:(13×2+14×6+15×8+16×3+17×2+18×1)÷22=15,
队员年龄的众数为15,队员年龄的中位数是15.
意义:由平均数是15可说明队员们的平均年龄为15岁;由众数是15可说明大多数队员的年龄为15岁;由中位数是15可说明有一半队员的年龄大于或等于15岁,有一半队员的年龄小于或等于15岁.
6.请根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
2
25-6-12-5=2(人),如图所示.
平均数(分) 中位数(分) 众数(分)
一班 a b 90
二班 87.6 80 c
(2)直接写出表格中a,b,c的值;
a=87.6,b=90,c=100
解:①一班和二班平均数相同,一班的中位数大于二班的中位数,故一班的成绩好于二班;
②一班和二班平均数相同,一班的众数小于二班的众数,故二班的成绩好于一班;
③B级以上(包括B级)一班18人,二班12人,故一班的成绩好于二班.
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面来比较一班和二班的成绩;
②从平均数和众数方面来比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
平均数、中位数和众数的应用
平均数、中位数、众数的实际应用
平均数、中位数、众数的特征
课堂小结
在一组数据中,出现次数最多的数
众数
第6章 数据的分析
6.1.3 众数
第6章 数据的分析
6.1 平均数、中位数、众数
学 习 目 标
1
理解众数的概念,会求一组数据的众数;(重点)
2
掌握众数的作用,会用众数分析实际问题. (难点)
了解平均数、中位数、众数各自的特点,能选择适当的量反映数据的集中趋势.(难点)
3
动脑筋
下面是一家鞋店在一段时间内各种尺码的男鞋的销售情况统计表:
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 10 17 10 12 7
新课导入
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 10 17 10 12 7
这家店销售量最多的男鞋是哪种尺码的?店主最关心的问题是什么?
这家店销售量最多的是25cm的鞋,店主最关心的就是销售量,所以店主下次进货时可以多进这个尺码的鞋.
在上面的问题中,25是鞋的尺码中出现次数最多的数,所以25是这组数据的众数.
鞋的尺码(cm) 23 23.5 24 24.5 25 25.5 26 26.5
销售量(双) 5 6 6 10 17 10 12 7
1.众数
在一组数据中,把出现次数最多的数叫做这组数据的众数.
当一组数据中某数据多次重复出现时,常可以用众数作为这组数据的数值的一个代表值.
一组数据的众数可以不止一个.
知识讲解
下表是某学习小组一次数学测验的成绩统计表:
已知该小组本次数学测验的平均分是85分,则测验成绩的众数是( )
A.80 分 B.85 分 C.90 分 D.80 分和90 分
解析:要确定众数,必须先确定x,
由平均数的概念可知70×1+80×3+90x+100×1 = 85(1+3+x+1),即410+90x = 425+85x,解得x = 3.
从而可知这组数据中80 和90 出现的次数最多,都是3 次,故众数有两个,80 分和90 分.
D
例1
注意:
(1)一组数据的众数一定出现在这组数据中.
(2)一组数据的众数可能不止一个.如1,1,2,3,3,
5中众数是1和3.
(3)众数是一组数据中出现次数最多的数据而不是数据出现的次数,如1,1,1,2,2,5中众数是1而不是3.
(4) 众数的单位与原数据的单位一致.
当数据组中数据重复出现的情况并不突出时,讨论众数
是没有意义的.
某公司全体职工的月工资如下:
试求出该公司工资数据中的众数、中位数和平均数.
月工资(元) 18000 12000 8000 6000 4000 2500 2000 1500 1200
人数 1 (总经理) 2 (副总经理) 3 4 10 20 22 12 6
2.平均数、中位数和众数的选择
例2
解: 在上述80个数据中,2000出现了22次,出现的
次数最多,因此这组数据的众数是2000.
出现次数最多的数
月工资(元) 18000 12000 8000 6000 4000 2500 2000 1500 1200
人数 1 (总经理) 2 (副总经理) 3 4 10 20 22 12 6
把这80个数据按从小到大的顺序排列后,可以
发现位于中间的数是2000,2500,因此这组数
据的中位数是
这组数据的平均数为
我们把这组数据的众数、中位数、平均数表示在图中:
议一议
在例2中,你认为用平均数、中位数或众数中的哪一个更能反映该公司的工资水平?
工资的平均数3115 偏高,因为大多数员工的工资都达不到这个平均数,用它来作为该公司员工工资的代表值并不合适.
众数是2000,中位数是2250,它们代表了大多数人的工资水平,不偏高也不偏低,较能反映工资水平的实际情况.
公司总经理最关心的是公司月工资的总额,所以他关注的是平均数.
普通员工关注的是自己的收入在本公司职工群体中的位置,中位数能帮助职工了解自己的工资收入是“中上”还是“中下”水平……
在例2中,对于职工月工资数据的平均数、中位数和众数,你认为该公司总经理、普通员工及应聘者将分别关注哪一个?说说你的理由, 并相互交流.
应聘者关注的是该公司月工资的众数,因为应聘者最想知道的是公司发给大多数员工的工资数,这也是一般的应聘者将会拿到的工资.
说一说
平均数、中位数和众数都是一组数据的代表,它们从不同侧面反映了数据的集中趋势.
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息,因此在现实生活中应用较广,但它容易受极端值的影响;
中位数对极端值不敏感,但没有利用数据中所有的信息;
众数只能反映一组数据中出现次数最多的数据,也没有利用数据中所有的信息.
归纳:平均数、众数和中位数这三个统计量各自的特点
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息.
归纳:平均数、众数和中位数这三个统计量各自的优点
众数是当一组数据中某一数据多次重复出现时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势;
中位数的计算很少,仅与数据的排列位置有关,不易受极端值影响,中位数可能出现在所给数据中,也可能不在所给数据中.
公园有甲、乙两队游客在做团体游戏,两队游客的年龄(单位:岁)如下:
例3
(1)分别算出两队游客年龄的平均数、众数和中位数.
(2)甲、乙两队游客年龄的平均数能代表他们各自的年龄特征吗?如果不能,哪个数据能代表?
分析:(1)将两组数据分别代入平均数的计算公式计算;根据中位数和众数的定义来分别确定甲、乙两队的中位数和众数.
(2)要判断平均数能否代表各组年龄的特征,就是要看平均数是否与各组数据反映的实际意义相吻合.
(2)甲队游客年龄的平均数能代表他们的年龄特征,乙队游客年龄的平均数不能代表他们的年龄特征.
对于乙队游客而言,10 人中有8 人的年龄在9 岁以下,而说他们的平均年龄是15 岁,会让人误认为这队游客的年龄都在15 岁左右,所以乙队的平均数不能代表该队游客年龄的特征. 可选用中位数或众数来代表乙队游客的年龄特征.
1.要调查多数同学们喜欢看的电视节目,应关注的是( )
A.平均数 B.中位数 C.众数
2.数据1,2, 8,5,3,9,5,4,5,4的众数分别为 .
C
随堂训练
5
3.下面的扇形图描述了某种运动服的S号、M号、L号、XL号、XXL号在一家商场的销售情况.请你为这家商场提出进货建议.
S
16%
8%
24%
30%
22%
M
L
XL
XXL
解:因为众数是M号,所以建议商场多进M号的运动服,其次是进S号,再其次进L号,少进XXL号的运动服.
4. 某校抽取八年级某班50名学生,调查他们一周做
家务所用时间,得到一组数据,并绘制成下表,请根
据下表完成各题:
每周做家务的时间(小时) 0 1 1.5 2 2.5 3 3.5 4
人数 2 2 6 12 13 4 3
(1)填写表格中未完成的部分;
(2)该班学生每周做家务的平均时间是 .
2.44
(3)这组数据的中位数是 ,众数是 .
2.5
3
8
5.某校男子足球队的年龄分布如下面的条形图所示.
请找出这些队员年龄的平均数、众数、中位数,
并解释它们的意义.
人数
13
14
15
16
17
18
年龄/岁
0
2
4
6
8
10
解:这些队员年龄的平均数为:(13×2+14×6+15×8+16×3+17×2+18×1)÷22=15,
队员年龄的众数为15,队员年龄的中位数是15.
意义:由平均数是15可说明队员们的平均年龄为15岁;由众数是15可说明大多数队员的年龄为15岁;由中位数是15可说明有一半队员的年龄大于或等于15岁,有一半队员的年龄小于或等于15岁.
6.请根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
2
25-6-12-5=2(人),如图所示.
平均数(分) 中位数(分) 众数(分)
一班 a b 90
二班 87.6 80 c
(2)直接写出表格中a,b,c的值;
a=87.6,b=90,c=100
解:①一班和二班平均数相同,一班的中位数大于二班的中位数,故一班的成绩好于二班;
②一班和二班平均数相同,一班的众数小于二班的众数,故二班的成绩好于一班;
③B级以上(包括B级)一班18人,二班12人,故一班的成绩好于二班.
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面来比较一班和二班的成绩;
②从平均数和众数方面来比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
平均数、中位数和众数的应用
平均数、中位数、众数的实际应用
平均数、中位数、众数的特征
课堂小结
在一组数据中,出现次数最多的数
众数
