教学课件:七下·湘教6.2 方差
图片预览








文档简介
(共24张PPT)
第6章 数据的分析
第6章 数据的分析
6.2 方差
学 习 目 标
1
2
理解方差的意义,学会如何刻画一组数据波动的大小.
掌握方差的计算公式,并会用它来解决一些实际问题.(重点、难点)
探索方差产生的过程,发展合情推理的能力.
3
动脑筋
刘亮和李飞参加射击训练的成绩(单位:环)如下:
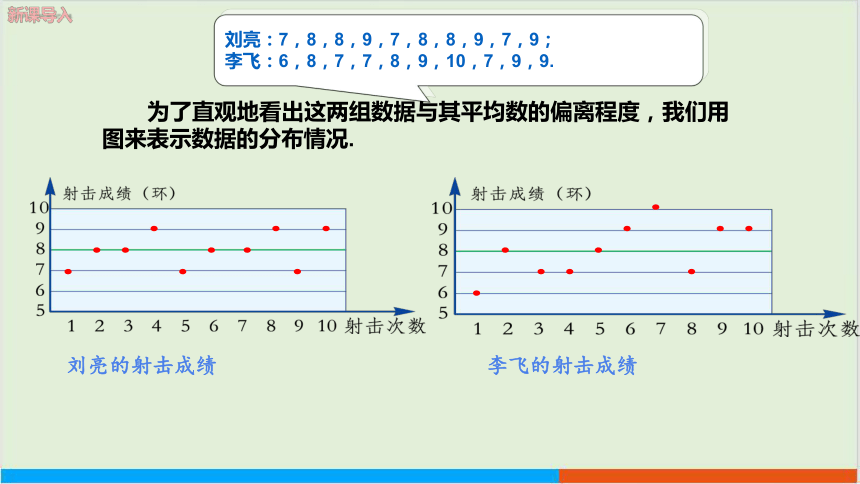
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
(1) 两人的平均成绩分别是多少?
(2) 如何反映这两组数据与其平均数的偏离程度?
(3) 谁的成绩比较稳定?
新课导入
刘亮成绩的平均数是
李飞成绩的平均数是
即两人的平均成绩相同.
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
为了直观地看出这两组数据与其平均数的偏离程度,我们用图来表示数据的分布情况.
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
刘亮的射击成绩
李飞的射击成绩
由上面两幅图,可以发现刘亮的射击成绩大多集中在平均成绩8环附近,
而李飞的射击成绩与其平均成绩的偏差较大.
那么如何找到一个特征值来反映一组数据与其平均数的离散程度呢?
将各个数与平均数之差相加. 但是相加的结果为0啊!
把各个数与平均数之差取绝对值,再取它们的平均值.
把各个数与平均数之差平方,再取它们的平均值.
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的离散程度或波动大小.
为了反映一组数据的离散程度,可以采用很多方法,统计中常采用以下做法:
设一组数据为x1,x2,…,xn,各数据与平均数
之差的平方的平均值,叫做这组数据的方差,记做 s2.
即
方差
1
知识讲解
计算方差的步骤可概括为“先平均,后求差,
平方后,再平均”.
由此我们可以算出刘亮、李飞的射击成绩的方差分别是
计算结果表明: s2李飞> s2刘亮,这说明李飞的射击成绩波动大,而刘亮的射击成绩波动小,因此刘亮的射击成绩稳定.
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
方差的意义
2
例1 有两个女声小合唱队,各由5名队员组成.
她们的身高为(单位:cm)为:
甲队:160,162,159,160,159;
乙队:180,160,150,150,160.
如果单从队员的身高考虑,哪队的演出效果好?
解 甲队队员的平均身高是
甲队队员身高的方差是
乙队队员的平均身高是
乙队队员身高的方差是
计算的结果表明:乙队队员身高的方差比甲队队员身高的方差大很多,这说明乙队中各队员的身高波动大,而甲队中各队员的身高波动小,所以甲队队员的身高比较整齐,形象效果好.
从例1的计算过程可以看到,求方差的运算量很大.
当一组数据所含的数很多时,我们可以借助计算器来求一组数据的方差.
不同型号的计算器其操作步骤可能不同,请先阅读计算器的说明书.通常先按统计键,使计算器进入统计运算模式,然后依次输入数据,最后按求方差的功能键,即可求出该组数据的方差.
用计算器求方差
3
练一练
1.用计算器求下列各组数据的平均数和方差:
(1)24,24,31,31,47,47,62,84,95,95;
(2)473,284,935,743,586,654;
(3)10.1,9.8,9.7,10.2,10.3,9.9,10.0 .
答:平均数为54,方差为728.2 .
答:平均数为612.5,方差为41805.58 .
答:平均数为10,方差为0.04.
2. 李明的班上要派一名选手参加学校田径运动会的
100m 比赛,李明和张亮都希望自己能参加比赛,
他们在训练中10次的测试成绩(单位:s)分别是:
李明:14.5,14.9,14.2,15.0,14.7,14.1,14.4,
13.9,15.5,14.8;
张亮:14.8,14.4,15.5,14.1,14.3,14.6,14.1,
14.8,15.1,14.3.
根据两人的成绩,应该派谁去参加比赛?
答:李明的平均成绩为14.6s .
张亮的平均成绩为14.6s.
李明成绩的方差为0.206.
张亮成绩的方差为0.186.
由于张亮成绩波动小,
所以应该派张亮去参加比赛.
例2 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团表演了舞剧《天鹅湖》,
参加表演的女演员的身高(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞团女演员的身高更整齐
解:甲乙两团女演员的平均身高分别是:
, 所以,甲芭蕾舞团女演员的身高更整齐.
因为
1、甲、乙两人在相同的条件下,各射靶10次,经过计算:
甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,
下列说法中不正确的是 ( )
A、甲、乙射中的总环数相同 B、甲的成绩较稳定
C、乙的成绩较稳定 D、乙的成绩波动较大
2、在样本方差的计算公式
数字10 表示 ,数字20表示 .
3、样本5、6、7、8、9的方差是 .
C
2
样本平均数
样本容量
ú
ù
ê
é
-
+
-
+
-
=
)
20
(
2
...
)
20
(
2
2
)
20
(
1
2
10
1
2
s
x
n
x
x
+
练一练
1.人数相同的八年级(1)、(2)两班学生在同
一次数学单元测试中,班级平均分和方差下:
, , 则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
2.
随堂训练
3.
4.
方差
意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小)
公式:
课堂小结
计算步骤:
“先平均,后求差,平方后,再平均”.
第6章 数据的分析
第6章 数据的分析
6.2 方差
学 习 目 标
1
2
理解方差的意义,学会如何刻画一组数据波动的大小.
掌握方差的计算公式,并会用它来解决一些实际问题.(重点、难点)
探索方差产生的过程,发展合情推理的能力.
3
动脑筋
刘亮和李飞参加射击训练的成绩(单位:环)如下:
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
(1) 两人的平均成绩分别是多少?
(2) 如何反映这两组数据与其平均数的偏离程度?
(3) 谁的成绩比较稳定?
新课导入
刘亮成绩的平均数是
李飞成绩的平均数是
即两人的平均成绩相同.
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
为了直观地看出这两组数据与其平均数的偏离程度,我们用图来表示数据的分布情况.
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
刘亮的射击成绩
李飞的射击成绩
由上面两幅图,可以发现刘亮的射击成绩大多集中在平均成绩8环附近,
而李飞的射击成绩与其平均成绩的偏差较大.
那么如何找到一个特征值来反映一组数据与其平均数的离散程度呢?
将各个数与平均数之差相加. 但是相加的结果为0啊!
把各个数与平均数之差取绝对值,再取它们的平均值.
把各个数与平均数之差平方,再取它们的平均值.
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的离散程度或波动大小.
为了反映一组数据的离散程度,可以采用很多方法,统计中常采用以下做法:
设一组数据为x1,x2,…,xn,各数据与平均数
之差的平方的平均值,叫做这组数据的方差,记做 s2.
即
方差
1
知识讲解
计算方差的步骤可概括为“先平均,后求差,
平方后,再平均”.
由此我们可以算出刘亮、李飞的射击成绩的方差分别是
计算结果表明: s2李飞> s2刘亮,这说明李飞的射击成绩波动大,而刘亮的射击成绩波动小,因此刘亮的射击成绩稳定.
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
方差的意义
2
例1 有两个女声小合唱队,各由5名队员组成.
她们的身高为(单位:cm)为:
甲队:160,162,159,160,159;
乙队:180,160,150,150,160.
如果单从队员的身高考虑,哪队的演出效果好?
解 甲队队员的平均身高是
甲队队员身高的方差是
乙队队员的平均身高是
乙队队员身高的方差是
计算的结果表明:乙队队员身高的方差比甲队队员身高的方差大很多,这说明乙队中各队员的身高波动大,而甲队中各队员的身高波动小,所以甲队队员的身高比较整齐,形象效果好.
从例1的计算过程可以看到,求方差的运算量很大.
当一组数据所含的数很多时,我们可以借助计算器来求一组数据的方差.
不同型号的计算器其操作步骤可能不同,请先阅读计算器的说明书.通常先按统计键,使计算器进入统计运算模式,然后依次输入数据,最后按求方差的功能键,即可求出该组数据的方差.
用计算器求方差
3
练一练
1.用计算器求下列各组数据的平均数和方差:
(1)24,24,31,31,47,47,62,84,95,95;
(2)473,284,935,743,586,654;
(3)10.1,9.8,9.7,10.2,10.3,9.9,10.0 .
答:平均数为54,方差为728.2 .
答:平均数为612.5,方差为41805.58 .
答:平均数为10,方差为0.04.
2. 李明的班上要派一名选手参加学校田径运动会的
100m 比赛,李明和张亮都希望自己能参加比赛,
他们在训练中10次的测试成绩(单位:s)分别是:
李明:14.5,14.9,14.2,15.0,14.7,14.1,14.4,
13.9,15.5,14.8;
张亮:14.8,14.4,15.5,14.1,14.3,14.6,14.1,
14.8,15.1,14.3.
根据两人的成绩,应该派谁去参加比赛?
答:李明的平均成绩为14.6s .
张亮的平均成绩为14.6s.
李明成绩的方差为0.206.
张亮成绩的方差为0.186.
由于张亮成绩波动小,
所以应该派张亮去参加比赛.
例2 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团表演了舞剧《天鹅湖》,
参加表演的女演员的身高(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞团女演员的身高更整齐
解:甲乙两团女演员的平均身高分别是:
, 所以,甲芭蕾舞团女演员的身高更整齐.
因为
1、甲、乙两人在相同的条件下,各射靶10次,经过计算:
甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,
下列说法中不正确的是 ( )
A、甲、乙射中的总环数相同 B、甲的成绩较稳定
C、乙的成绩较稳定 D、乙的成绩波动较大
2、在样本方差的计算公式
数字10 表示 ,数字20表示 .
3、样本5、6、7、8、9的方差是 .
C
2
样本平均数
样本容量
ú
ù
ê
é
-
+
-
+
-
=
)
20
(
2
...
)
20
(
2
2
)
20
(
1
2
10
1
2
s
x
n
x
x
+
练一练
1.人数相同的八年级(1)、(2)两班学生在同
一次数学单元测试中,班级平均分和方差下:
, , 则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
2.
随堂训练
3.
4.
方差
意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小)
公式:
课堂小结
计算步骤:
“先平均,后求差,平方后,再平均”.
