7.2 相交线 教案
图片预览




文档简介
7.2 相交线
第1课时 相交所成的角
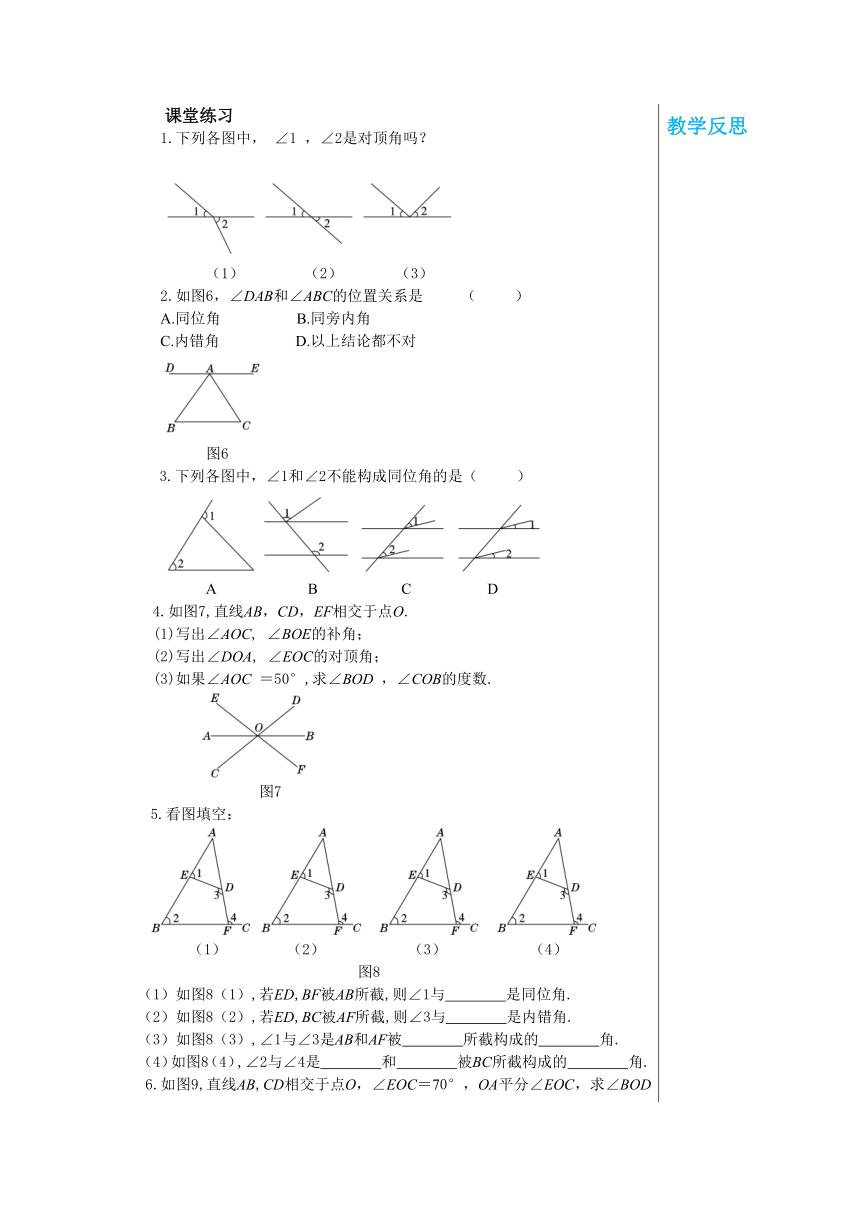
教学目标1.理解并掌握对顶角的概念,了解对顶角、同位角、内错角、同旁内角的概念.2.通过观察、探究,辨别同位角、内错角、同旁内角,培养学生对图形的辨别能力.教学重难点重点:理解并掌握对顶角的概念,了解对顶角、同位角、内错角、同旁内角的概念.难点:通过观察、探究,辨别同位角、内错角、同旁内角,培养学生对图形的辨别能力.教学过程导入新课在同一平面上任意画两条直线,这两条直线的位置关系有几种可能?当同一平面内两条直线只有一个公共点时,是什么位置关系?学生动手画,体会同一平面上任意两条直线存在两种位置关系,即相交和不相交(平行).在同一平面内,有一个公共点的两条直线叫做相交线.多媒体展示图片.教师同时提问:观察这些图片,从中你们看到了哪些相交线和平行线?学生发言,相互补充.教师:在现实生活中,你们还能找到哪些形如相交线、平行线的实例?学生积极踊跃发言,相互补充.教师总结:同学们对相交线、平行线一定不陌生,大桥上的钢梁和钢索、棋盘上的横线和竖线、笔直的高速公路……都给我们相交线、平行线的形象.从这一章开始,我们正式开始研究平面内不重合的两条直线的位置关系.今天这节课,我们研究相交线.探究新知一、对顶角图1从画的图中我们可以看出,两条直线相交有四个角:∠1,∠2,∠3,∠4. 1.我们看∠1和∠3的顶点、两条边有什么关系?①具有公共顶点;②两边互为反向延长线. 学生小组讨论,得出对顶角的概念:具有公共顶点,并且两边互为反向延长线的两个角,叫做对顶角.2.除了∠1和∠3是对顶角,还有其他的对顶角吗?∠1和∠2是对顶角吗?图中∠2与∠4 是对顶角,∠1和∠2不是对顶角.练一练:下列各图中,∠1与∠2是对顶角吗?为什么?(1) (2) (3)(4) (5) (6)(只有(4)是对顶角)学生独立完成后指名学生回答,出现问题让其他学生纠正.二、对顶角的性质如图2,两条直线,相交于点O. 图21.观察:当一条直线绕点O转动时,∠1和∠3的变化情况.(同时增大或同时减小) 2.猜想:∠1与∠3的大小关系.(∠1=∠3)3.讨论:请用适当的方法验证你的猜想.(量角器测量,逻辑推理)学生合作学习,经各组充分实验、讨论、交流后,阐述本组观点并给出讨论结果.对于问题3,鼓励学生采用实验的方法进行验证.已知:如图3,∠1与∠3是对顶角.图3求证:∠1=∠3.证明:因为 ∠1与∠2互补,∠2与∠3互补,所以 ∠1=∠3 (同角的补角相等).同理 ∠2=∠4.通过刚才的说理验证,引出对顶角的性质:对顶角相等.想一想:图中是对顶角量角器,你能说出用它测量角的原理吗?例 如图4,直线a,b相交,∠1=40°,求 ∠2,∠3,∠4的度数.图4∵ ∠3=∠1,∠1=40°, ∴ ∠3=40°,∴ ∠2=180°-∠1=140°,∴ ∠4=∠2=140°.三、三线八角多媒体出示教材第36页“观察与思考”,让学生进行思考:图5如图5,一条直线c分别与两条直线a,b相交(也说直线a,b被直线c所截),构成八个角.(三线八角) (1)观察∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8的位置关系,试描述它们的位置特征. (2)∠3和∠6,∠4和∠5各有什么位置特征? (3)∠3和∠5, ∠4和∠6有什么位置特征?学生独立思考,个别回答,发现结论不一致,加以讨论并及时纠正.(1)观察∠4和∠8,分别在直线a,b的同侧,在直线c的同旁;∠3和∠7分别在直线a,b的同侧,直线c的同旁,把具有这样位置的一对角,叫做同位角. 同位角,顾名思义,被截线的同一位置.如果去掉多余的线,呈现的基本图形,很像我们的英文字母“F”.图中的同位角除∠4和∠8、∠3和∠7外,还有哪些角是同位角?(∠1和∠5,∠2和∠6)(2)观察∠3和∠6,分别在直线a,b的内部,在直线c的两旁, 把具有∠3和∠6这样位置关系的一对角,叫做内错角. 内错角, 顾名思义,在被截线内部交错的角.如果去掉多余的线,呈现的基本图形,很像我们的英文字母“Z”.图中的内错角除∠3和∠6外,还有哪些角是内错角? (∠4和∠ 5)(3)我们把具有∠3与∠5这样位置的一对角,叫做同旁内角.你能说出具有什么关系的一对角叫做同旁内角吗? 同旁内角是指位于直线c的同旁,直线a和b内部的两个角.同旁内角, 顾名思义,在截线的同旁. 如果去掉多余的线,呈现的基本图形,很像我们的英文字母“U”. 图中还有同旁内角吗?(∠4与∠6)引导学生把同位角、内错角、同旁内角的位置特征及图形特征列成表:角的名称位置特征基本图形图形结构特征同位角在截线同侧,在被截两直线同一方形如字母“F”(或倒置、反置、旋转)内错角在截线两侧(交错),在被截两直线之间形如字母“Z”(或倒置、反置、旋转)同旁内角在截线同一旁,在被截两直线之间形如字母“U”(或倒置、反置、旋转)大家共同总结三种特殊角的特征.你能看出三种角的共同特征吗 教师再强调同位角、内错角、同旁内角虽然在位置上有差别,但它们都有一个共同特点,都有一条边在同一截线上,同学们往往忽视这一前提因而发生判断错误.练一练:识别哪些角是同位角、内错角、同旁内角.课堂练习1.下列各图中, ∠1 ,∠2是对顶角吗?(1) (2) (3)2.如图6,∠DAB和∠ABC的位置关系是 ( ) A.同位角 B.同旁内角 C.内错角 D.以上结论都不对图6 3.下列各图中,∠1和∠2不能构成同位角的是( )A B C D4.如图7,直线AB,CD,EF相交于点O. (1)写出∠AOC, ∠BOE的补角; (2)写出∠DOA, ∠EOC的对顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数. 图75.看图填空: (1) (2) (3) (4) 图8(1)如图8(1),若ED,BF被AB所截,则∠1与 是同位角.(2)如图8(2),若ED,BC被AF所截,则∠3与 是内错角.(3)如图8(3),∠1与∠3是AB和AF被 所截构成的 角.(4)如图8(4),∠2与∠4是 和 被BC所截构成的 角. 6.如图9,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,求∠BOD的度数. 图9 7.拓展题:观察下列各图,寻找对顶角(不含平角)图a 图b 图c⑴ 如图a,图中共有_______对对顶角;⑵ 如图b,图中共有_______对对顶角;⑶ 如图c,图中共有_______对对顶角;⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成_______对对顶角;⑸ 若有10条直线相交于一点,则可形成_______对对顶角.参考答案1.解:(1)不是,(2)是,(3)不是. 2.C 3.D 4.解:(1)∠AOC的补角是∠AOD和∠COB;∠BOE的补角是∠EOA和∠BOF.(2)∠DOA的对顶角是∠COB;∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°;∠COB=180°-∠AOC=130°.5.(1)∠2 (2)∠4 (3)DE 内错 (4)AB AF 同位6.解:∵ OA平分∠EOC,∠EOC=70°, ∴ ∠AOC=∠EOC=35°, ∴ ∠BOD=∠AOC=35°. 7.(1)2(2)6(3)12(4)n(n-1)(5)90课堂小结 布置作业教材第37页习题A组题.板书设计7.2 相交线第1课时 相交所成的角 对顶角 对顶角的性质 教学反思教学反思教学反思教学反思教学反思教学反思教学反思
7.2 相交线
第2课时 垂直
可归纳为“一落、二过、三画”.
3.三画:沿着直角边经过已知点画直线.
通过画图,教师引导学生归纳结论.基本事实:经过直线上或直线外一点,有且只有一条直线与已知直线垂直.注意:1.“过一点”中的点,可以在已知直线上,也可以在已知直线外.2.“有且只有”中,“有”指存在性,“只有”指唯一性.三、点到直线的距离 如图,C是直线AB外一点,且CD⊥AB,垂足为D,即CD是点C到直线AB的垂线段.再经过点C向直线AB任意引两条线段CE,CF. (1)猜想线段CD,CE,CF哪一条最短. (2)以点C为圆心,CD的长为半径画弧,圆弧分别与线段CE,CF相交于点E1,F1.线段CE1,CD,CF1相等吗?由此能进一步验证你的猜想吗?教师针对学生回答进行点评. 通过上面的探究,我们得到:直线外一点与直线上各点连接的所有线段中,垂线段最短. 我们把垂线段CD的长度称为点C到直线AB的距离.试一试:在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.课堂练习1.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )A.相等 B.互余 C.互补 D.互为对顶角2.如图,点C到直线AB的距离是指( )A.线段AC的长度 B.线段CD的长度 C.线段BC的长度 D.线段BD的长度3.如图, AC⊥BC, ∠CDB=90° ,线段AC,BC,CD中最短的是( )A. AC B. BC C. CD D. 不能确定4.如图,直线AB,CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为________. 5.下面四种判定两条直线垂直的方法,正确的有____________. ①两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直;②两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直;③两条直线相交,所成的四个角相等,则这两条直线互相垂直;④两条直线相交,有一组对顶角互补,则这两条直线互相垂直.6.如图,已知直线AB,CD相交于点O,且OE⊥AB.(1)过点O画直线MN⊥CD;(2)若点F是(1)中所画直线MN上任意一点(O点除外),若∠AOC=35°,求∠EOF的度数.参考答案1.B 2.B 3.C 4.32°5.①②③④6.解:(1)如图所示.(2)①当点F在射线OM上时.因为OE⊥AB,MN⊥CD,所以∠EOB=∠MOD=90°,所以∠EOF+∠EOD=90°,∠EOD+∠BOD=90°,所以∠EOF=∠BOD=∠AOC=35°.②当点F在射线ON上时,如图中点F′.因为MN⊥CD,所以∠MOC=90°=∠AOC+∠AOM,所以∠AOM=90°-∠AOC=55°,所以∠BON=∠AOM=55°,所以∠EOF′=∠EOB+∠BON=90°+55°=145°.综上所述,∠EOF的度数是35°或145°. 课堂小结1.两条直线相交,当它们的交角有一个是90°时,叫做这两条直线互相垂直.如图,记作:AB⊥CD,垂足是O.2.经过直线上或直线外一点,有且只有一条直线与已知直线垂直.3.直线外一点与直线上各点连接的所有线段中,垂线段最短.我们把垂线段的长度叫做这个点到直线的距离.4.会用三角尺或量角器过一点画已知直线的垂线. 布置作业教材第40页习题A组题.板书设计7.2 相交线 第2课时 垂直垂线 垂线段垂线的画法 垂线段的性质 基本事实 点到直线的距离 教学反思教学反思教学反思教学反思教学反思教学反思
对顶角相等.
同位角
内错角
同旁内角
第1课时 相交所成的角
教学目标1.理解并掌握对顶角的概念,了解对顶角、同位角、内错角、同旁内角的概念.2.通过观察、探究,辨别同位角、内错角、同旁内角,培养学生对图形的辨别能力.教学重难点重点:理解并掌握对顶角的概念,了解对顶角、同位角、内错角、同旁内角的概念.难点:通过观察、探究,辨别同位角、内错角、同旁内角,培养学生对图形的辨别能力.教学过程导入新课在同一平面上任意画两条直线,这两条直线的位置关系有几种可能?当同一平面内两条直线只有一个公共点时,是什么位置关系?学生动手画,体会同一平面上任意两条直线存在两种位置关系,即相交和不相交(平行).在同一平面内,有一个公共点的两条直线叫做相交线.多媒体展示图片.教师同时提问:观察这些图片,从中你们看到了哪些相交线和平行线?学生发言,相互补充.教师:在现实生活中,你们还能找到哪些形如相交线、平行线的实例?学生积极踊跃发言,相互补充.教师总结:同学们对相交线、平行线一定不陌生,大桥上的钢梁和钢索、棋盘上的横线和竖线、笔直的高速公路……都给我们相交线、平行线的形象.从这一章开始,我们正式开始研究平面内不重合的两条直线的位置关系.今天这节课,我们研究相交线.探究新知一、对顶角图1从画的图中我们可以看出,两条直线相交有四个角:∠1,∠2,∠3,∠4. 1.我们看∠1和∠3的顶点、两条边有什么关系?①具有公共顶点;②两边互为反向延长线. 学生小组讨论,得出对顶角的概念:具有公共顶点,并且两边互为反向延长线的两个角,叫做对顶角.2.除了∠1和∠3是对顶角,还有其他的对顶角吗?∠1和∠2是对顶角吗?图中∠2与∠4 是对顶角,∠1和∠2不是对顶角.练一练:下列各图中,∠1与∠2是对顶角吗?为什么?(1) (2) (3)(4) (5) (6)(只有(4)是对顶角)学生独立完成后指名学生回答,出现问题让其他学生纠正.二、对顶角的性质如图2,两条直线,相交于点O. 图21.观察:当一条直线绕点O转动时,∠1和∠3的变化情况.(同时增大或同时减小) 2.猜想:∠1与∠3的大小关系.(∠1=∠3)3.讨论:请用适当的方法验证你的猜想.(量角器测量,逻辑推理)学生合作学习,经各组充分实验、讨论、交流后,阐述本组观点并给出讨论结果.对于问题3,鼓励学生采用实验的方法进行验证.已知:如图3,∠1与∠3是对顶角.图3求证:∠1=∠3.证明:因为 ∠1与∠2互补,∠2与∠3互补,所以 ∠1=∠3 (同角的补角相等).同理 ∠2=∠4.通过刚才的说理验证,引出对顶角的性质:对顶角相等.想一想:图中是对顶角量角器,你能说出用它测量角的原理吗?例 如图4,直线a,b相交,∠1=40°,求 ∠2,∠3,∠4的度数.图4∵ ∠3=∠1,∠1=40°, ∴ ∠3=40°,∴ ∠2=180°-∠1=140°,∴ ∠4=∠2=140°.三、三线八角多媒体出示教材第36页“观察与思考”,让学生进行思考:图5如图5,一条直线c分别与两条直线a,b相交(也说直线a,b被直线c所截),构成八个角.(三线八角) (1)观察∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8的位置关系,试描述它们的位置特征. (2)∠3和∠6,∠4和∠5各有什么位置特征? (3)∠3和∠5, ∠4和∠6有什么位置特征?学生独立思考,个别回答,发现结论不一致,加以讨论并及时纠正.(1)观察∠4和∠8,分别在直线a,b的同侧,在直线c的同旁;∠3和∠7分别在直线a,b的同侧,直线c的同旁,把具有这样位置的一对角,叫做同位角. 同位角,顾名思义,被截线的同一位置.如果去掉多余的线,呈现的基本图形,很像我们的英文字母“F”.图中的同位角除∠4和∠8、∠3和∠7外,还有哪些角是同位角?(∠1和∠5,∠2和∠6)(2)观察∠3和∠6,分别在直线a,b的内部,在直线c的两旁, 把具有∠3和∠6这样位置关系的一对角,叫做内错角. 内错角, 顾名思义,在被截线内部交错的角.如果去掉多余的线,呈现的基本图形,很像我们的英文字母“Z”.图中的内错角除∠3和∠6外,还有哪些角是内错角? (∠4和∠ 5)(3)我们把具有∠3与∠5这样位置的一对角,叫做同旁内角.你能说出具有什么关系的一对角叫做同旁内角吗? 同旁内角是指位于直线c的同旁,直线a和b内部的两个角.同旁内角, 顾名思义,在截线的同旁. 如果去掉多余的线,呈现的基本图形,很像我们的英文字母“U”. 图中还有同旁内角吗?(∠4与∠6)引导学生把同位角、内错角、同旁内角的位置特征及图形特征列成表:角的名称位置特征基本图形图形结构特征同位角在截线同侧,在被截两直线同一方形如字母“F”(或倒置、反置、旋转)内错角在截线两侧(交错),在被截两直线之间形如字母“Z”(或倒置、反置、旋转)同旁内角在截线同一旁,在被截两直线之间形如字母“U”(或倒置、反置、旋转)大家共同总结三种特殊角的特征.你能看出三种角的共同特征吗 教师再强调同位角、内错角、同旁内角虽然在位置上有差别,但它们都有一个共同特点,都有一条边在同一截线上,同学们往往忽视这一前提因而发生判断错误.练一练:识别哪些角是同位角、内错角、同旁内角.课堂练习1.下列各图中, ∠1 ,∠2是对顶角吗?(1) (2) (3)2.如图6,∠DAB和∠ABC的位置关系是 ( ) A.同位角 B.同旁内角 C.内错角 D.以上结论都不对图6 3.下列各图中,∠1和∠2不能构成同位角的是( )A B C D4.如图7,直线AB,CD,EF相交于点O. (1)写出∠AOC, ∠BOE的补角; (2)写出∠DOA, ∠EOC的对顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数. 图75.看图填空: (1) (2) (3) (4) 图8(1)如图8(1),若ED,BF被AB所截,则∠1与 是同位角.(2)如图8(2),若ED,BC被AF所截,则∠3与 是内错角.(3)如图8(3),∠1与∠3是AB和AF被 所截构成的 角.(4)如图8(4),∠2与∠4是 和 被BC所截构成的 角. 6.如图9,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,求∠BOD的度数. 图9 7.拓展题:观察下列各图,寻找对顶角(不含平角)图a 图b 图c⑴ 如图a,图中共有_______对对顶角;⑵ 如图b,图中共有_______对对顶角;⑶ 如图c,图中共有_______对对顶角;⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成_______对对顶角;⑸ 若有10条直线相交于一点,则可形成_______对对顶角.参考答案1.解:(1)不是,(2)是,(3)不是. 2.C 3.D 4.解:(1)∠AOC的补角是∠AOD和∠COB;∠BOE的补角是∠EOA和∠BOF.(2)∠DOA的对顶角是∠COB;∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°;∠COB=180°-∠AOC=130°.5.(1)∠2 (2)∠4 (3)DE 内错 (4)AB AF 同位6.解:∵ OA平分∠EOC,∠EOC=70°, ∴ ∠AOC=∠EOC=35°, ∴ ∠BOD=∠AOC=35°. 7.(1)2(2)6(3)12(4)n(n-1)(5)90课堂小结 布置作业教材第37页习题A组题.板书设计7.2 相交线第1课时 相交所成的角 对顶角 对顶角的性质 教学反思教学反思教学反思教学反思教学反思教学反思教学反思
7.2 相交线
第2课时 垂直
可归纳为“一落、二过、三画”.
3.三画:沿着直角边经过已知点画直线.
通过画图,教师引导学生归纳结论.基本事实:经过直线上或直线外一点,有且只有一条直线与已知直线垂直.注意:1.“过一点”中的点,可以在已知直线上,也可以在已知直线外.2.“有且只有”中,“有”指存在性,“只有”指唯一性.三、点到直线的距离 如图,C是直线AB外一点,且CD⊥AB,垂足为D,即CD是点C到直线AB的垂线段.再经过点C向直线AB任意引两条线段CE,CF. (1)猜想线段CD,CE,CF哪一条最短. (2)以点C为圆心,CD的长为半径画弧,圆弧分别与线段CE,CF相交于点E1,F1.线段CE1,CD,CF1相等吗?由此能进一步验证你的猜想吗?教师针对学生回答进行点评. 通过上面的探究,我们得到:直线外一点与直线上各点连接的所有线段中,垂线段最短. 我们把垂线段CD的长度称为点C到直线AB的距离.试一试:在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.课堂练习1.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )A.相等 B.互余 C.互补 D.互为对顶角2.如图,点C到直线AB的距离是指( )A.线段AC的长度 B.线段CD的长度 C.线段BC的长度 D.线段BD的长度3.如图, AC⊥BC, ∠CDB=90° ,线段AC,BC,CD中最短的是( )A. AC B. BC C. CD D. 不能确定4.如图,直线AB,CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为________. 5.下面四种判定两条直线垂直的方法,正确的有____________. ①两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直;②两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直;③两条直线相交,所成的四个角相等,则这两条直线互相垂直;④两条直线相交,有一组对顶角互补,则这两条直线互相垂直.6.如图,已知直线AB,CD相交于点O,且OE⊥AB.(1)过点O画直线MN⊥CD;(2)若点F是(1)中所画直线MN上任意一点(O点除外),若∠AOC=35°,求∠EOF的度数.参考答案1.B 2.B 3.C 4.32°5.①②③④6.解:(1)如图所示.(2)①当点F在射线OM上时.因为OE⊥AB,MN⊥CD,所以∠EOB=∠MOD=90°,所以∠EOF+∠EOD=90°,∠EOD+∠BOD=90°,所以∠EOF=∠BOD=∠AOC=35°.②当点F在射线ON上时,如图中点F′.因为MN⊥CD,所以∠MOC=90°=∠AOC+∠AOM,所以∠AOM=90°-∠AOC=55°,所以∠BON=∠AOM=55°,所以∠EOF′=∠EOB+∠BON=90°+55°=145°.综上所述,∠EOF的度数是35°或145°. 课堂小结1.两条直线相交,当它们的交角有一个是90°时,叫做这两条直线互相垂直.如图,记作:AB⊥CD,垂足是O.2.经过直线上或直线外一点,有且只有一条直线与已知直线垂直.3.直线外一点与直线上各点连接的所有线段中,垂线段最短.我们把垂线段的长度叫做这个点到直线的距离.4.会用三角尺或量角器过一点画已知直线的垂线. 布置作业教材第40页习题A组题.板书设计7.2 相交线 第2课时 垂直垂线 垂线段垂线的画法 垂线段的性质 基本事实 点到直线的距离 教学反思教学反思教学反思教学反思教学反思教学反思
对顶角相等.
同位角
内错角
同旁内角
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
