7.4 平行线的判定 教案

7.4 平行线的判定
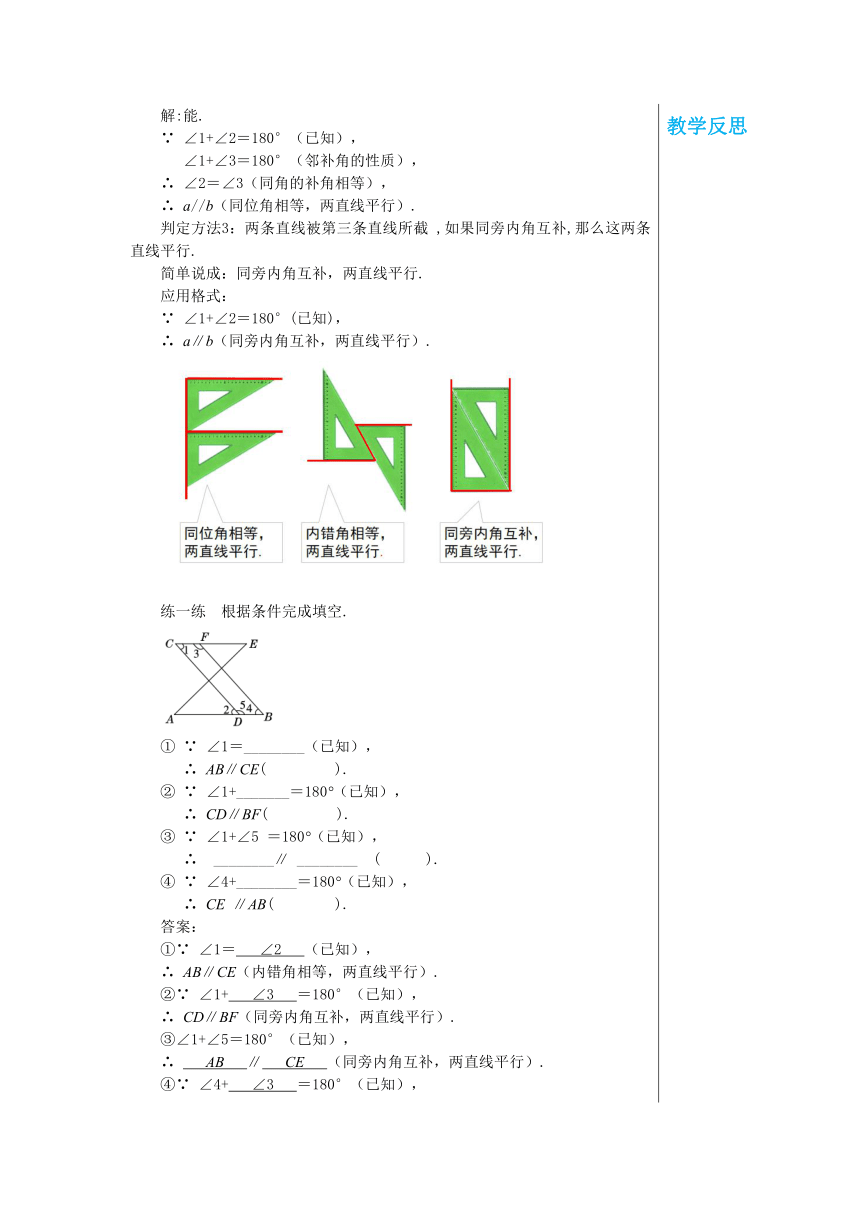
教学目标1.掌握平行线的三种判定方法，会运用判定方法来判断两条直线是否平行.2.会综合运用平行线的判定和性质解题.教学重点难点重点：掌握平行线的三种判定方法，会运用判定方法来判断两条直线是否平行.难点：会综合运用平行线的判定和性质解题.教学过程导入新课问题1：我们已学过的判定直线平行的方法有哪些？1.平行线的定义. 2.同位角相等，两直线平行.学生活动：学生口答以上两种方法问题2：两条直线被第三条直线所截，形成的角中有同位角、内错角、同旁内角，同位角相等，两直线平行，那么，利用内错角、同旁内角的关系，能否判定两直线平行呢？探究新知采用探讨问题的方式，启发学生去思考，能不能从内错角之间的关系或同旁内角之间的关系来判定两条直线平行呢？问题1：如图，由∠3＝∠2，可推出a//b吗？如何推出的呢？结合图形引导学生用符号语言表述推理过程.解： ∵ ∠1＝∠3(对顶角相等)， ∠3＝∠2（已知）， ∴ ∠1＝∠2， ∴ a//b(同位角相等，两直线平行）.判定方法2：两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.简单说成：内错角相等，两直线平行.应用格式：∵ ∠3＝∠2(已知)，∴ a∥b（内错角相等，两直线平行）.问题2：如图，如果∠1+∠2＝180°，你能判定a//b吗 结合图形引导学生用符号语言表述推理过程.解:能. ∵ ∠1+∠2＝180°（已知）， ∠1+∠3＝180°（邻补角的性质），∴ ∠2＝∠3（同角的补角相等），∴ a//b（同位角相等，两直线平行）.判定方法3：两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.简单说成：同旁内角互补，两直线平行.应用格式：∵ ∠1+∠2＝180°(已知)，∴ a∥b（同旁内角互补，两直线平行）.练一练 根据条件完成填空. ① ∵ ∠1＝________（已知）， ∴ AB∥CE( ).② ∵ ∠1+_______＝180°（已知）， ∴ CD∥BF( ).③ ∵ ∠1+∠5 ＝180°（已知）， ∴ ________∥ ________ ( ). ④ ∵ ∠4+________＝180°（已知）， ∴ CE ∥AB( ).答案：①∵ ∠1＝ ∠2 （已知），∴ AB∥CE（内错角相等，两直线平行）.②∵ ∠1+ ∠3 ＝180°（已知），∴ CD∥BF（同旁内角互补，两直线平行）.③∠1+∠5＝180°（已知），∴ AB ∥ CE （同旁内角互补，两直线平行）.④∵ ∠4+ ∠3 ＝180°（已知），∴ CE∥AB（同旁内角互补，两直线平行）.例 如图，已知直线AB，CD被直线EF所截， ∠1＝60°，∠2＝120°.对AB∥CD说明理由.教师活动：引导学生回忆平行线的判定的三种方法，然后分别用这三种方法做题.方法1理由：∵ ∠1＝60°，∠1+∠5＝180°（平角定义）， ∴ ∠5＝120°. 又∵∠2＝∠5＝120°， ∴ AB∥CD（同位角相等，两直线平行）.方法2理由：∵ ∠2＝120°，∠2+∠3＝180°（平角定义）， ∴ ∠3＝60°. 又∵ ∠1＝∠3＝60°， ∴ AB∥CD（内错角相等，两直线平行）.方法3理由：∵ ∠2＝120°，∠2＝∠4（对顶角相等）， ∴ ∠4＝120°. 又∵ ∠1＝60°， ∴ ∠1+∠4＝60°+120°＝180°（等量代换）， ∴ AB∥CD（同旁内角互补，两直线平行）.课堂练习1.如图,可以确定AB∥CE的条件是( )A.∠2＝∠B B. ∠1＝∠AC. ∠3＝∠B D. ∠3＝∠A 第1题图 第2题图2.如图，下列说法错误的是(　　)A．若a∥b，b∥c，则a∥cB．若∠1＝∠2，则a∥cC．若∠3＝∠2，则b∥cD．若∠3＋∠4＝180°，则a∥c3.如图,已知∠1＝30°,∠2或∠3满足条件___________，则a//b. 第3题图4.如图，给出下列条件：①∠B＋∠BCD＝180°；②∠1＝∠2；③∠3＝∠4；④∠B＝∠5；⑤∠B＝∠D.其中，一定能判定AB∥CD的条件有 _________ (填写所有正确的序号). 第4题图 第5题图5.如图，已知CB平分∠ACD，且∠1＝∠2，AB与CD平行吗？为什么？学生思考，教师巡视.参考答案：1.C 2.C 3.∠2＝150°或∠3＝30° 4.①③④5.解：平行.理由如下：∵ CB平分∠ACD，∴ ∠1＝∠BCD.∵ ∠1＝∠2，∴ ∠2＝∠BCD，∴ AB∥CD(内错角相等，两直线平行)．课堂小结 判定两条直线平行的方法文字叙述符号语言图形同位角相等，两直线平行∵ ∠1＝∠2（已知），∴ a∥b内错角相等，两直线平行∵ ∠3＝∠2（已知），∴ a∥b同旁内角互补，两直线平行∵ ∠2+∠4＝180°（已知），∴ a∥b 布置作业教材第47~48页习题A组，B组题.板书设计7.4 平行线的判定判定方法二：内错角相等，两直线平行.判定方法三：同旁内角互补，两直线平行. 教学反思教学反思教学反思教学反思教学反思