新课标A版必修5正弦定理(浙江省衢州市)
文档属性
| 名称 | 新课标A版必修5正弦定理(浙江省衢州市) |  | |
| 格式 | rar | ||
| 文件大小 | 279.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-01 23:24:00 | ||
图片预览







文档简介
课件37张PPT。正弦定理正弦定理:在一个三角形中,各边和它所对角的
正弦的比相等.即利用三角形面积来证有:剖析定理、加深理解正弦定理可以解决三角形中哪类问题:① 已知两角和一边,求其他角和边. ②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.定理的应用例 1在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b (精确到0.01).解: 且 ∵19.32=已知两角和任意边,
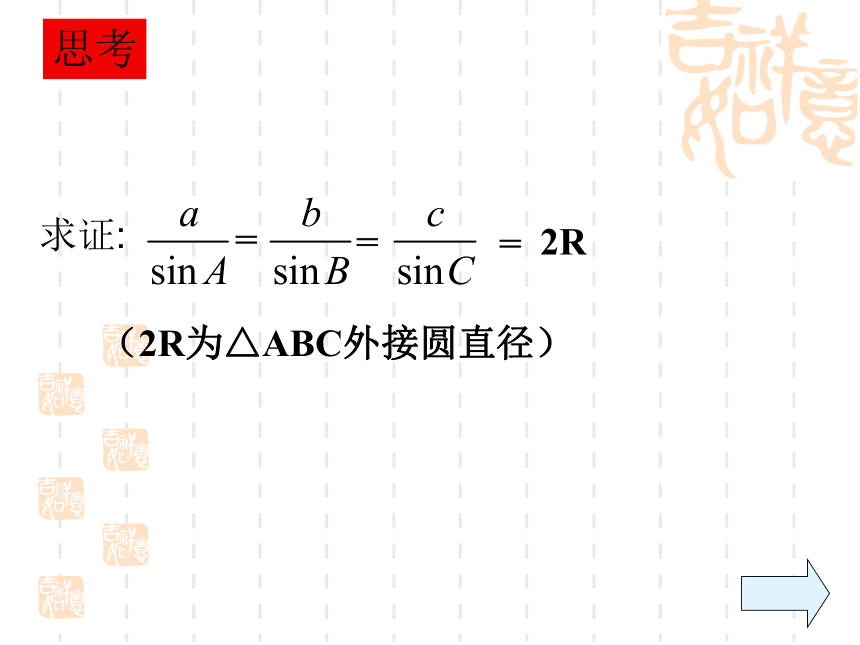
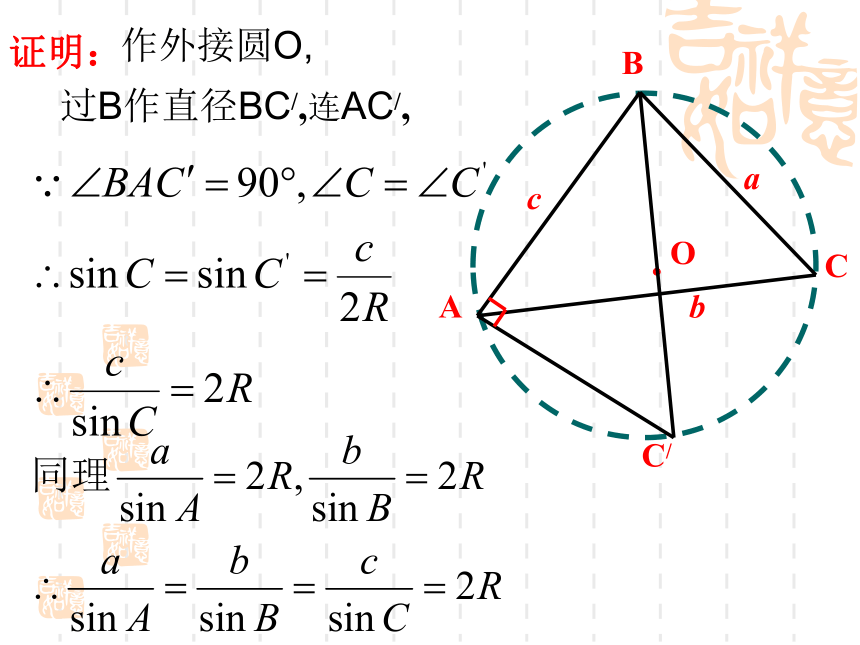
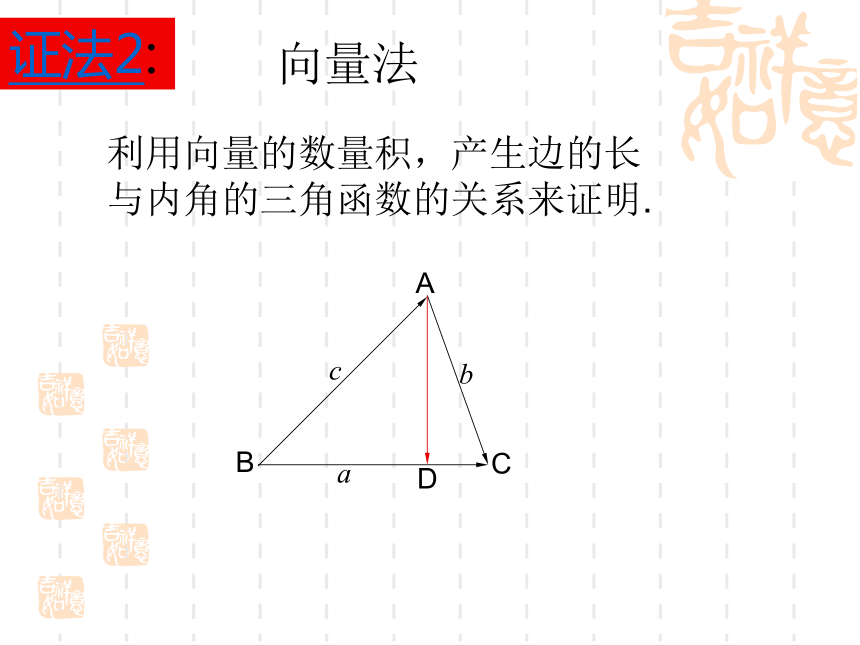
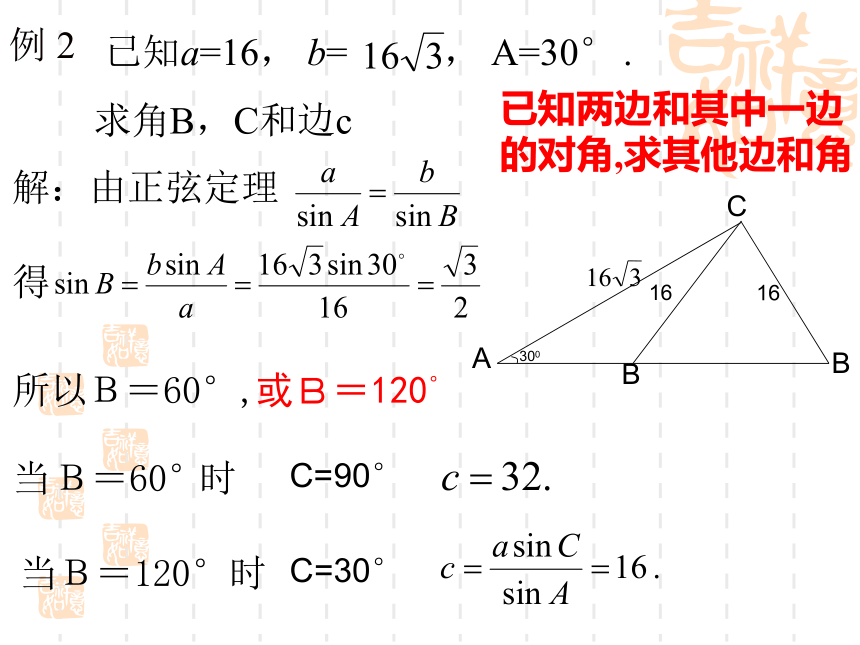
求其他两边和一角∵14.14=a(2R为△ABC外接圆直径)=2R思考求证:证明:作外接圆O,过B作直径BC/,连AC/,AcbCBDa向量法证法2:利用向量的数量积,产生边的长与内角的三角函数的关系来证明.例 2 已知a=16, b= , A=30° .
求角B,C和边c已知两边和其中一边
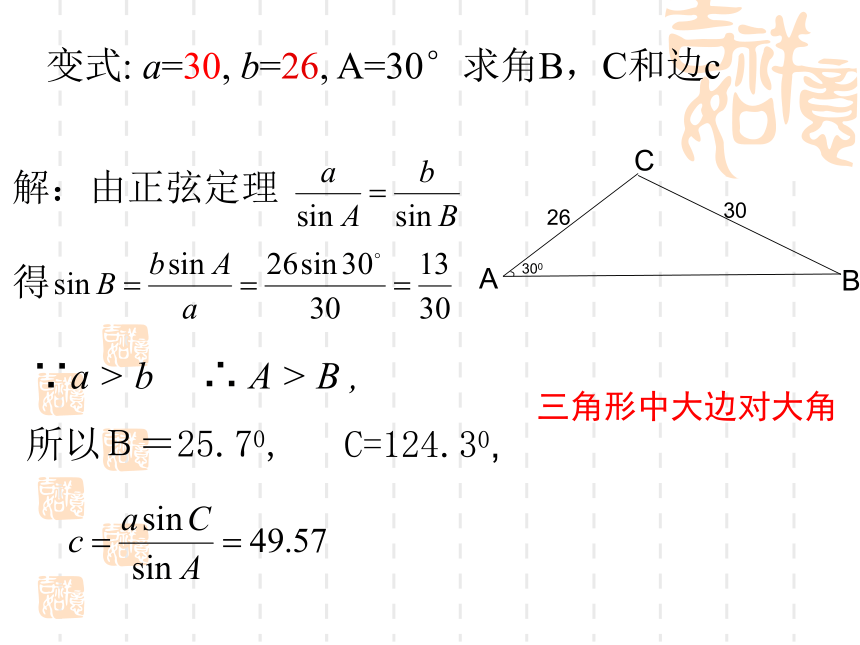
的对角,求其他边和角解:由正弦定理得所以B=60°,或B=120°C=90°C=30°当B=120°时变式: a=30, b=26, A=30°求角B,C和边c
由于154.30 +300>1800故B只有一解 (如图)C=124.30,变式: a=30, b=26, A=30°求角B,C和边c
所以B=25.70,C=124.30,∵a > b ∴ A > B ,三角形中大边对大角已知两边和其中一边的对角,求其他边和角1.根据下列条件解三角形 (1)b=13,a=26,B=30°.[B=90°,C=60°,c= ](2) b=40,c=20,C=45°.练习注:三角形中角的正弦值小于1时,角可能有两解无解课堂小结(1)三角形常用公式:(2)正弦定理应用范围:① 已知两角和任意边,求其他两边和一角 ②
已知两边和其中一边的对角,求另一边
的对角。(注意解的情况)正弦定理:已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考谢谢大家ACabab 一解实际问题分析:要求BC,只要求AB,为此考虑解
△ABD解:过点D作DE//AC交BC于E,因为
∠DAC=20°,所以∠ADE=160°,于是∠ADB=360°-160°-65°=135°又∠BAD=35 ° -20 ° =15,所以
∠ABD=30 °在△ABD中,由正弦定理,得在Rt△ABC中,BC=ABsin35°=答:山的高度为811m.例4、在三角形ABC中,已知 ,
试判断三角形ABC的形状.解:令 ,由正弦定理,得a=ksinA,b=ksinB,c=ksinC.代入已知条件,得即tanA=tanB=tanC又A,B,C∈(0,π),所以A=B=C,
从而三角形ABC为正三角形.练习1、如图,要测底部不能到达的烟囱的高AB,从与烟囱底
部在同一水平直线上的C、D两处,测得烟囱的仰角分别是 ,CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。图中给出了怎样的一个
几何图形?已知什么,
求什么?想一想实例讲解实例讲解分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:答:烟囱的高为 29.9m.正弦定理的综合应用A 解斜三角形的问题,通常都要根据题意,从实际问题中抽象
出一个或几个三角形,然后通过解这些三角形,得出所要求的量,
从而得到实际问题的解。 在这个过程中,贯穿了数学建模的思想。这种思想即是从实际
问题出发,经过抽象概括,把它转化为具体问题中的数学模型,
然后通过推理演算,得出数学模型的解,再还原成实际问题的解。本节小结:
正弦的比相等.即利用三角形面积来证有:剖析定理、加深理解正弦定理可以解决三角形中哪类问题:① 已知两角和一边,求其他角和边. ②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.定理的应用例 1在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b (精确到0.01).解: 且 ∵19.32=已知两角和任意边,
求其他两边和一角∵14.14=a(2R为△ABC外接圆直径)=2R思考求证:证明:作外接圆O,过B作直径BC/,连AC/,AcbCBDa向量法证法2:利用向量的数量积,产生边的长与内角的三角函数的关系来证明.例 2 已知a=16, b= , A=30° .
求角B,C和边c已知两边和其中一边
的对角,求其他边和角解:由正弦定理得所以B=60°,或B=120°C=90°C=30°当B=120°时变式: a=30, b=26, A=30°求角B,C和边c
由于154.30 +300>1800故B只有一解 (如图)C=124.30,变式: a=30, b=26, A=30°求角B,C和边c
所以B=25.70,C=124.30,∵a > b ∴ A > B ,三角形中大边对大角已知两边和其中一边的对角,求其他边和角1.根据下列条件解三角形 (1)b=13,a=26,B=30°.[B=90°,C=60°,c= ](2) b=40,c=20,C=45°.练习注:三角形中角的正弦值小于1时,角可能有两解无解课堂小结(1)三角形常用公式:(2)正弦定理应用范围:① 已知两角和任意边,求其他两边和一角 ②
已知两边和其中一边的对角,求另一边
的对角。(注意解的情况)正弦定理:已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考谢谢大家ACaba
△ABD解:过点D作DE//AC交BC于E,因为
∠DAC=20°,所以∠ADE=160°,于是∠ADB=360°-160°-65°=135°又∠BAD=35 ° -20 ° =15,所以
∠ABD=30 °在△ABD中,由正弦定理,得在Rt△ABC中,BC=ABsin35°=答:山的高度为811m.例4、在三角形ABC中,已知 ,
试判断三角形ABC的形状.解:令 ,由正弦定理,得a=ksinA,b=ksinB,c=ksinC.代入已知条件,得即tanA=tanB=tanC又A,B,C∈(0,π),所以A=B=C,
从而三角形ABC为正三角形.练习1、如图,要测底部不能到达的烟囱的高AB,从与烟囱底
部在同一水平直线上的C、D两处,测得烟囱的仰角分别是 ,CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。图中给出了怎样的一个
几何图形?已知什么,
求什么?想一想实例讲解实例讲解分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:答:烟囱的高为 29.9m.正弦定理的综合应用A 解斜三角形的问题,通常都要根据题意,从实际问题中抽象
出一个或几个三角形,然后通过解这些三角形,得出所要求的量,
从而得到实际问题的解。 在这个过程中,贯穿了数学建模的思想。这种思想即是从实际
问题出发,经过抽象概括,把它转化为具体问题中的数学模型,
然后通过推理演算,得出数学模型的解,再还原成实际问题的解。本节小结:
