2024年中考数学总复习验收卷(二)(含解析)
文档属性
| 名称 | 2024年中考数学总复习验收卷(二)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 21:25:02 | ||
图片预览



文档简介
2024年中考数学总复习验收卷(二)
数学试卷
考试范围:初中;考试时间:120分钟;满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题只有一个正确答案,每小题3分,满分30分)
1.的倒数的绝对值是( )
A. B. C. D.
2.下列我国四家航空公司的logo图案,中心对称图形是( )
A.B. C.D.
3.下列各式计算正确的是( )
A. B. C. D.
4.一组数据4,5,,7,9的平均数为6,则这组数据的众数为( )
A.4 B.5 C.7 D.9
5.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果,那么的度数是( )
A.22° B.32° C.38° D.44°
6.一个由相同小立方块搭成的几何体,从正面、左面、上面看到的形状图如图所示,则搭成这个几何体的小立方块的个数为( )
A.4个 B.5个 C.6个 D.7个
7.将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A.B.C.D.
8.王芳同学到文具店购买中性笔和笔记本.中性笔每支0.8元,笔记本每本1.2元,王芳带了10元钱,则可供她选择的购买方案的个数为( )(两样都买,余下的钱少于0.8元)
A.6 B.7 C.8 D.9
9.在一个不透明的口袋中装有若干个只有颜色不同的白球和黄球,如果袋中黄球的个数是白球的两倍,那么摸到白球的概率为( )
A. B. C. D.不能确定
10.如图,二次函数()的图象与轴交于A,B两点,与轴交于点C,点A坐标为(-1,0),点C在(0,2)与(0,3)之间(不包括这两点),抛物线的顶点为D,对称轴为直线=2.有以下结论:①;②若点M(,),点N(,)是函数图象上的两点,则;③<<;④不可能是等腰直角三角形.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,满分21分)
11.随着电子技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.00000065m2.这个数用科学记数法表示为_____m2.
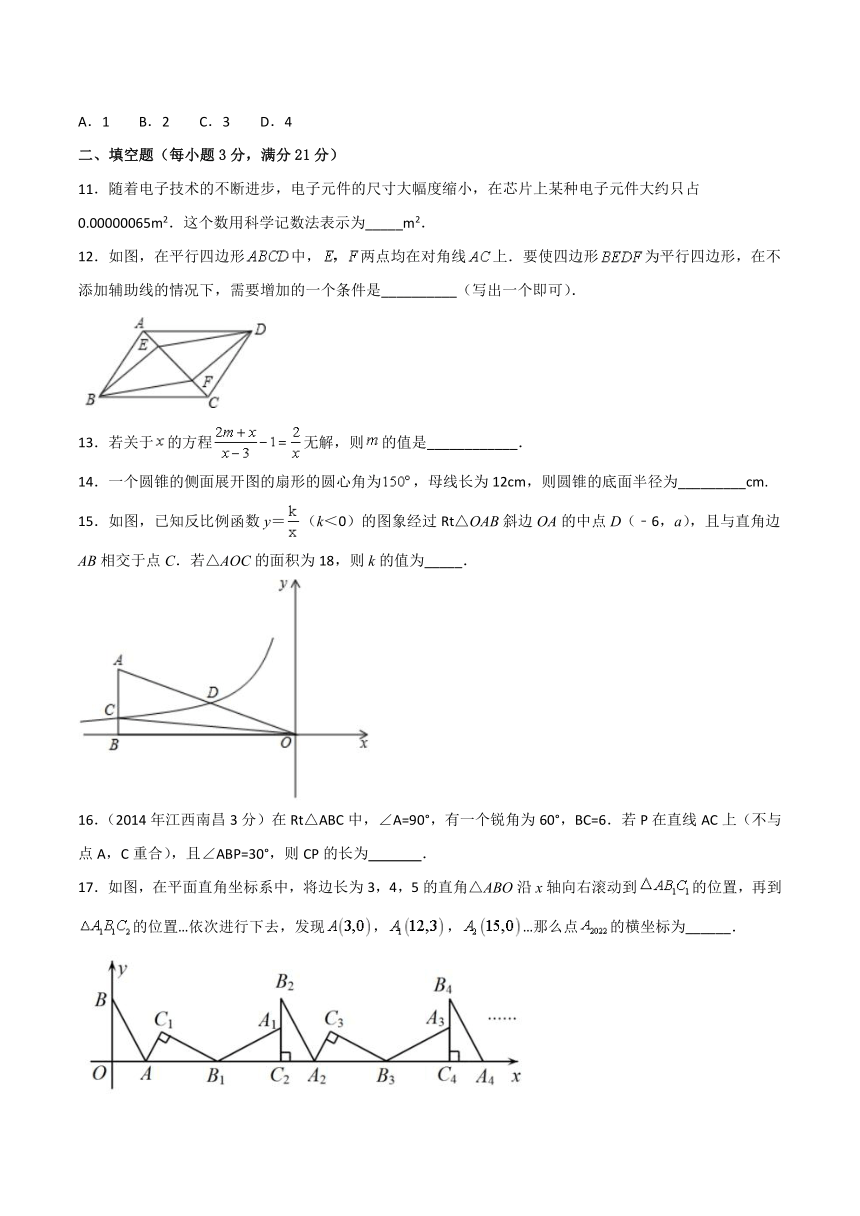
12.如图,在平行四边形中,两点均在对角线上.要使四边形为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是__________(写出一个即可).
13.若关于的方程无解,则的值是____________.
14.一个圆锥的侧面展开图的扇形的圆心角为,母线长为12cm,则圆锥的底面半径为_________cm.
15.如图,已知反比例函数y=(k<0)的图象经过Rt△OAB斜边OA的中点D(﹣6,a),且与直角边AB相交于点C.若△AOC的面积为18,则k的值为_____.
16.(2014年江西南昌3分)在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为 .
17.如图,在平面直角坐标系中,将边长为3,4,5的直角△ABO沿x轴向右滚动到的位置,再到的位置…依次进行下去,发现,,…那么点的横坐标为______.
三、解答题(共7道大题,共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)计算:;
(2)因式分解:
19.(本题满分5分)解方程:
20.(本题满分8分)某地区在所有中学开展《老师,我想对你说》心灵信箱活动,为师生之间的沟通增设了一个书面交流的渠道.为了解两年来活动开展的情况,某课题组从全地区随机抽取部分中学生进行问卷调查.对“两年来,你通过心灵信箱给老师总共投递过封信?”这一调查项设有四个回答选项,选项A:没有投过;选项B:一封;选项C:两;选项D:三封及以上.根据接受问卷调查学生的回答,统计出各选项的人数以及所占百分比,分别绘制成如下条形统计图和扇形统计图:
(1)此次抽样调查了 名学生,条形统计图中m= ,n= ;
(2)请将条形统计图补全;
(3)接受问卷调查的学生在活动中投出的信件总数至少有 封;
(4)全地区中学生共有110000名,由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有多少名?
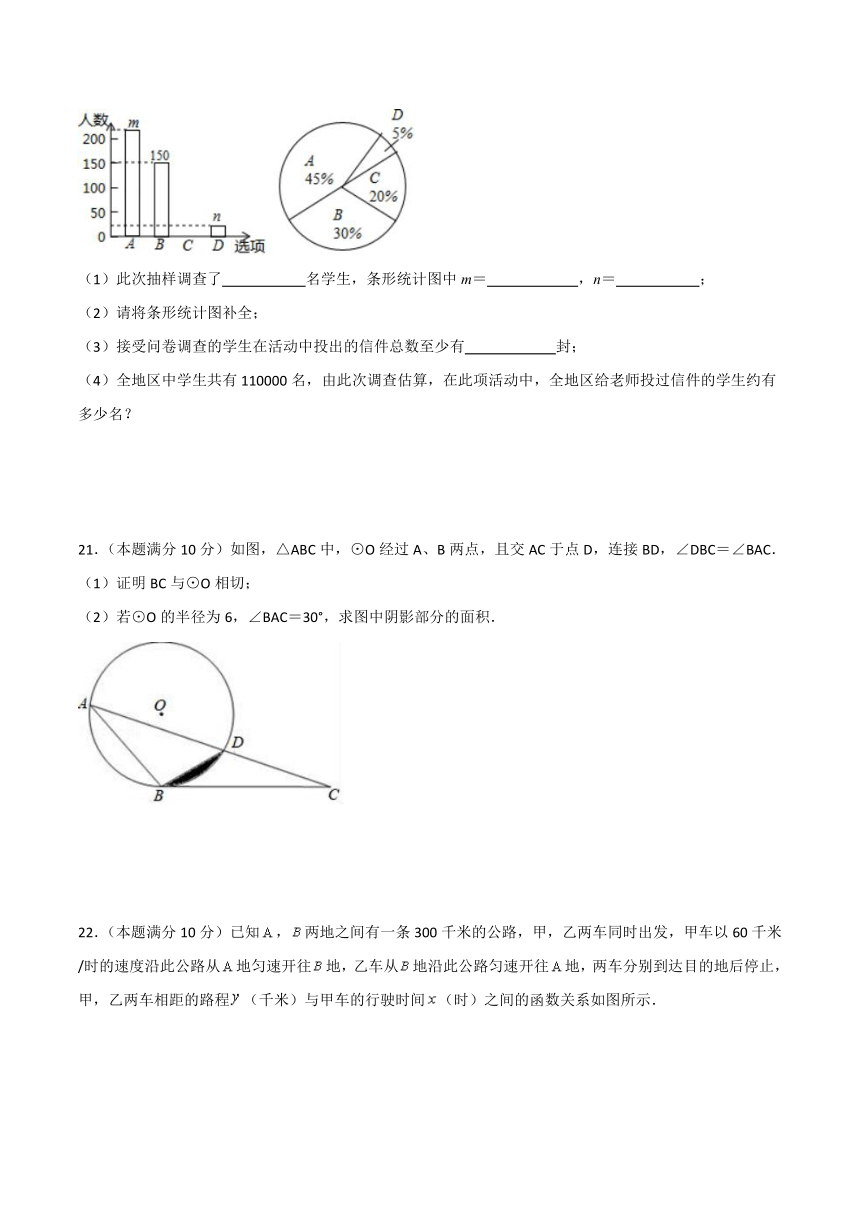
21.(本题满分10分)如图,△ABC中,⊙O经过A、B两点,且交AC于点D,连接BD,∠DBC=∠BAC.
(1)证明BC与⊙O相切;
(2)若⊙O的半径为6,∠BAC=30°,求图中阴影部分的面积.
22.(本题满分10分)已知,两地之间有一条300千米的公路,甲,乙两车同时出发,甲车以60千米/时的速度沿此公路从地匀速开往地,乙车从地沿此公路匀速开往地,两车分别到达目的地后停止,甲,乙两车相距的路程(千米)与甲车的行驶时间(时)之间的函数关系如图所示.
(1)乙车的速度为______千米/时,______,______.
(2)求甲,乙两车相遇后与之间的函数关系式.
(3)当甲车到达距地120千米处时,直接写出甲,乙两车之间的路程.
23.综合与实践(本题满分12分)在数学研究课上,老师出示如图1所示的长方形纸条,,,然后在纸条上任意画一条截线段,将纸片沿折叠,与交于点,得到,如图2所示:
(1)若,求的大小;
(2)改变折痕位置,判断的形状,并说明理由;
(3)爱动脑筋的小明在研究的面积时,发现边上的高始终是个不变的值.根据这一发现,他很快研究出的面积最小值为,求的大小;
(4)小明继续动手操作,发现了面积的最大值,请你求出这个最大值.
24.综合与探究(本题满分14分)如图,抛物线与轴相交于,两点,与轴相交于点,,,直线是抛物线的对称轴,在直线右侧的抛物线上有一动点,连接,,,.
(1)求抛物线的函数表达式:
(2)若点在轴的下方,当的面积是时,求的面积;
(3)在直线上有一点,连接,,则的最小值为______;
(4)在(2)的条件下,点是轴上一点,点是抛物线上一动点,是否存在点,使得以点,,,为顶点的四边形是平行四边形,若存在,请直接写出点的坐标;若不存在,请说明理由.
参考答案:
1.B
【分析】根据题意,要先求出倒数,然后再求绝对值.
【详解】解:的倒数是,的绝对值是.
故选:B .
【点睛】本题考查有理数的倒数和绝对值,熟练掌握倒数和绝对值的计算方法是关键.
2.A
【分析】根据中心对称图形的定义逐一判断即可.
【详解】选项B、C、D都不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形,
选项A能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形,
故选:A
【点睛】本题考查了中心对称图形识别,熟练掌握中心对称图形的定义是解题关键.
3.A
【分析】根据合并同类项法则、完全平方公式、同底数幂的除法和幂的乘方法则进行计算即可.
【详解】解:A. ,计算正确,符合题意;
B. ,原计算错误,不合题意;
C. ,原计算错误,不合题意;
D. ,原计算错误,不合题意,
故选:A.
【点睛】本题考查了合并同类项法则、完全平方公式、同底数幂的除法和幂的乘方法则,熟练掌握各运算法则是解题的关键.
4.B
【分析】先根据平均数的公式计算出x的值,再求这组数据的众数即可.
【详解】解:∵4,5,,7,9的平均数为6,
∴,
解得:x=5,
∴这组数据为:4,5,5,7,9,
∴这组数据的众数为5.
故选:B.
【点睛】本题考查平均数及众数,熟练掌握平均数、众数的意义是解题的关键.
5.C
【分析】根据BE∥CD得到∠EBC=22°,依据∠ABC=60°,∠EBC=22°,由角的和差关系可求∠2=38°.
【详解】解:如图,
∵BE∥CD,
∴∠EBC=∠1=22°,
∵∠ABC=60°,
∴∠2=38°.
故选:C.
【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,内错角相等.
6.B
【分析】从俯视图中可以看出最底层小立方块的个数及形状,从主视图可以看出每一层小立方块的层数和个数,从左视图可看出每一行小立方块的层数和个数,从而算出总的个数.
【详解】解:如图所示,
由俯视图易得:最底层小立方块的个数为4,由其他视图可知第二层有1个小立方块,那么共有个小立方块.
故选:B.
【点睛】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
7.B
【解析】根据将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水,即可求出小水杯内水面的高度h(cm)与注水时间t(min)的函数图象.
解:将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,小玻璃杯内的水原来的高度一定大于0,则可以判断A、D一定错误,用一注水管沿大容器内壁匀速注水,水开始时不会流入小玻璃杯,因而这段时间h不变,当大杯中的水面与小杯水平时,开始向小杯中流水,h随t的增大而增大,当水注满小杯后,小杯内水面的高度h不再变化.
故选B.
8.B
【分析】设购买x支中性笔,y本笔记本,根据题意得出:9.2<0.8x+1.2y≤10,进而求出即可.
【详解】解;设购买x支中性笔,y本笔记本,根据题意得出:
9.2<0.8x+1.2y≤10,
当x=2时,y=7,
当x=3时,y=6,
当x=5时,y=5,
当x=6时,y=4,
当x=8时,y=3,
当x=9时,y=2,
当x=11时,y=1,
故一共有7种方案.
故选:B.
【点睛】此题主要考查了二元一次方程的应用,得出不等关系是解题关键.
9.A
【分析】先设袋中白球的个数为x个,然后根据概率公式列式计算即可.
【详解】解:设袋中白球的个数为x个,则黄球的个数2x,
∴摸到白球的概率==,
故选A.
【点睛】本题考查了概率公式的应用,设出未知数、并运用概率公式列出方程是解答本题的关键.
10.C
【分析】由,得,由点坐标与点坐标得,,由二次函数图象可知,则,得出,故①正确;
点,关于对称轴的对称点为,,,随的增大而增大,则,故②不正确;
由,解得,故③正确;
易求,,则是等腰三角形,如果是等腰直角三角形,则点到的距离等于,则,求出二次函数解析式为,当时,,与点在与之间(不包括这两点)矛盾,得出不可能是等腰直角三角形,故④正确.
【详解】二次函数的对称轴为:,
,
,
点坐标为,点在与之间,且都在抛物线上,
,,
由二次函数图象可知,,
,
又,
,故①正确;
点,关于对称轴的对称点为,,,随的增大而增大,
,故②不正确;
,
解得:,
故③正确;
抛物线的顶点为,对称轴为直线,
点与点关于直线对称,点在直线上,
,,
是等腰三角形,
如果是等腰直角三角形,则点到的距离等于,即,
则,
解得:,
二次函数解析式为:,
当时,,与点在与之间(不包括这两点)矛盾,
不可能是等腰直角三角形,故④正确;
正确的有3个,
故选:C.
【点睛】本题考查二次函数的图象与性质、二次函数解析式的求法、等腰三角形的判定等知识,解题的关键是熟练掌握二次函数的图象与性质,属于中考常考题型.
11.6.5×10﹣7
【详解】试题分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00000065=6.5×10﹣7.
故答案为6.5×10﹣7.
12.(答案不唯一)
【分析】连接BD交AC于点O,由平行四边形的性质可得到OB=OD,要证明四边形BEDF为平行四边形,只需要OE=OF即可,故添加的条件只要能证明OE=OF即可.
【详解】如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
∴OB=OD,OA=OC,
若AE=CF,则有AO-AE=CO-CF,即OE=OF,
∴四边形BEDF为平行四边形,
故答案为:AE=CF.答案不唯一.
【点睛】本题主要考查平行四边形的判定,掌握平行四边形的判定方法是解题的关键.即①两组对边分别平行的四边形是平行四边形,②两组对边分别相等的四边形是平行四边形,③一组对边平行且相等的四边形是平行四边形,④两组对角分别相等的四边形是平行四边形,⑤对角线互相平分的四边形是平行四边形.
13.或
【分析】将分式方程转化为整式方程,分整式方程无解和分式方程有增根两种情况求解即可.
【详解】解:,
方程两边同乘:,得:,
整理得:,
①整式方程无解:,解得:;
②分式方程有增根:或,解得:或;
当时:整式方程无解;
当时:,解得:;
综上,当或时,分式方程无解;
故答案为:或.
【点睛】本题考查分式方程无解问题.熟练掌握整式方程无解或分式方程有增根时,分式方程无解,是解题的关键.
14.
【分析】设圆锥的底面半径为,根据侧面展开图的扇形的弧长等于底面圆的周长,据此作答即可.
【详解】解:设圆锥的底面半径为,
则,
解得:,
故答案为:.
【点睛】考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于侧面展开扇形的弧长,难度不大.
15.-12
【分析】设点A的坐标为(b,c),则点D的坐标为,首先通过点D在反比例函数图像上得出bc=4k,再通过点C在反比例函数图象上得出,然后利用S△AOB﹣S△BOC=S△AOC即可求出k的值.
【详解】设点A的坐标为(b,c),则点D的坐标为(),
∵点D在反比例函数图象上,
∴
化简得:bc=4k,
又∵∠ABO=90°,
点C在反比例函数图象上,
∴,
又∵S△AOB﹣S△BOC=S△AOC,
∴,
解得:k=﹣12,
故答案为:﹣12.
【点睛】本题主要考查反比例函数与几何综合,掌握反比例函数图象上的点满足反比例函数解析式是解题的关键.
16.,或6
【解析】试题分析:根据题意画出图形,分四种情况讨论:
①如答图1:当∠C=60°时,∠ABC=30°,P点在线段AC上,∠ABP不可能等于30°,只能是P点与C点重合,与条件相矛盾.
②如答图2:当∠C=60°时,∠ABC=30°,P点在线段CA的延长上.
∵Rt△ABC中,BC=6,∠C=30°,∴AC=BC=×6=3.
在△ABC和△ABP中,∵∠ABP=∠ABC=30°,AB=AB,∠CAB=∠PAB=90°,
∴△ABC≌△ABP(ASA).∴AC=AP=3.∴CP=AC+AP=3+3=6.
③如图3:当∠ABC=60°时,∠C=30°,P点在线段AC上.
∵Rt△ABC中,BC=6,∠C=30°,∴AB=BC=×6=3.
∵∠ABP=30°,∴AP=BP,∠PBC=∠ABC-∠ABP=60°-30°=30°=∠C.∴PC=PB.
∵在Rt△ABP中, ,∴,解得PB=.
∴PC=PB=.
④如答图4:当∠ABC=60°时,∠C=30°,P点在线段CA的延长线上.
∵∠ABP=30°,∠ABC=60°,∴△PBC是直角三形.
∵∠C=30°,∴PB=PC.
∵在 Rt△PBC中,PC2-PB2=BC2,∴,解得PC=.
综上所述,CP的长为,或6.
考点:1.含30度直角三角形的性质;2.全等三角形的判定和性质;3.勾股定理;4. 分类思想的应用.
17.12135
【分析】根据直角的边长求出点 ,再由沿轴向右滚动到的位置,再到的位置…依次进行下去,即可找到规律,即可求解.
【详解】∵ , , , ,
根据题意知: ,
得:;
继续滚动得:;
发现规律:,
∵ ,解得:
则 ,
∴点的横坐标为,
故答案为:.
【点睛】本题主要考查了规律型:点的坐标,找到规律是解题的关键.
18.(1);(2).
【详解】解:(1)原式 .
(2)
=
=
=
=.
19.【答案】,-3.
【解析】
解:x2+5x+6=0
(x+2)(x+3)=0
x+2=0或x+3=0
,-3.
20.(1)500,225,25;(2)补全图形见解析;(3)425;(4)全地区给老师投过信件的学生约有60500名.
【分析】(1)由B选项人数及其所占百分比求得总人数,再用总人数乘以对应百分比可得m、n的值;
(2)先求出C选项的人数,继而可补全图形;
(3)各选项次数乘以对应人数,再求和即可得;
(4)利用样本估计总体思想求解可得.
【详解】(1)此次调查的总人数为150÷30%=500(人),
则m=500×45%=225,n=500×5%=25,
故答案为500,225,25;
(2)C选项人数为500×20%=100(人),
补全图形如下:
(3)1×150+2×100+3×25=425,
答:接受问卷调查的学生在活动中投出的信件总数至少有425封,
故答案为425;
(4)由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有110000×(1﹣45%)=60500(名).
【点睛】本题考查了条形统计图,扇形统计图,用样本估计总体,准确识图,从中找到必要的信息是解题的关键.
21.(1)证明见解析;(2)6π-9.
【分析】(1)连接BO并延长交⊙O于点E,连接DE.由圆周角定理得出∠BDE=90°,再求出∠EBD+∠DBC=90°,根据切线的判定定理即可得出BC是⊙O的切线;
(2)分别求出等边三角形DOB的面积和扇形DOB的面积,即可求出答案.
【详解】(1)证明:连接BO并延长交⊙O于点E,连接DE,
∵BE是直径,∴∠EDB=90°,
∴∠E+∠EBD=90°
∵=,∴∠E=∠A
又∵∠DBC=∠BAC,∴∠DBC=∠E
∴∠DBC+∠EBD=90°,∴∠EBC=90°,∴BC⊥EB.
又∵OB是半径(B在⊙O上),∴BC与⊙O相切.
(2)∵=,∴∠BOD=2∠A=60°
S阴影= S扇形OBD-S△OBD=π36×-9=6π-9.
【点睛】本题考查了切线的判定,圆周角定理,扇形面积,等边三角形的性质和判定的应用,关键是求出∠EBD+∠DBC=90°和分别求出扇形DOB和三角形DOB的面积.
22.(1)90,,5;(2);(3)150千米.
【分析】(1)根据图象可知2小时后相遇,根据路程和为270千米即可求求出乙车的速度;然后根据路程、速度、时间的关系确定;
(2)运用待定系数法求解即可;
(3)求出甲车到达距地120千米处的时间,带入求解即可;
【详解】(1)乙车的速度为:千米/时,
,
,
故答案为:90,,5.
(2)(千米),
当时,设,
把(2,0),代入;
,
∴,
∴,
当时,设,把点代入可得,
∴,
综上,;
(3)甲车到达距地120千米处的时间为:(小时),
此时的路程为:(千米);
∴甲,乙两车之间的路程150千米.
【点睛】本题主要考查了一次函数的图象应用,准确分析计算是解题的关键.
23.(1)∠MKN=40°;(2)等腰三角形;(3)45°或135°;(4)△MNK的面积最大值为1.3.
【分析】(1)根据矩形的性质和折叠的性质求出∠KNM,∠KMN的度数,根据三角形内角和即可求解;
(2)利用翻折变换的性质以及两直线平行内错角相等得出KM=KN;
(3)利用当△KMN的面积最小值为时,KN=BC=1,故KN⊥B′M,得出∠1=∠NMB=45°,同理当将纸条向下折叠时,∠1=∠NMB=135°;
(4)分情况一:将矩形纸片对折,使点B与D重合,此时点K也与D重合;情况二:将矩形纸片沿对角线AC对折,此时折痕即为AC两种情况讨论求解.
【详解】(1)如图1,
∵四边形ABCD是长方形,
∴AM∥DN,
∴∠KNM=∠1,
∵∠1=70°,
∴∠KNM=∠KMN=∠1=70°,
∴∠MKN=40°;
(2)等腰三角形,理由如下:
∵AM∥BN,∴∠1=∠MND,
∵将纸片沿MN折叠,∴∠1=∠KMN,∠MND=∠KMN,
∴KM=KN,
故的形状是等腰三角形;
(3)如图2,当△KMN的面积最小值为时,KN=BC=1,故KN⊥B′M,
∵∠NMB=∠KMN,∠KMB=90°,
∴∠1=∠NMB=45°,
同理当将纸条向下折叠时,∠1=∠NMB=135°,
所以∠1的度数为45°或135°;
(4)分两种情况:
情况一:如图3,将矩形纸片对折,使点B与D重合,此时点K也与D重合,
MK=MB=x,则AM=5﹣x,
由勾股定理得12+(5﹣x)2=x2,
解得x=2.6,
∴MD=ND=2.6,
S△MNK=S△MND=×1×2.6=1.3;
情况二:如图4,将矩形纸片沿对角线AC对折,此时折痕即为AC,
MK=AK=CK=x,则DK=5﹣x,
同理可得MK=NK=2.6,
∵MD=1,
∴S△MNK=×1×2.6=1.3,
所以△MNK的面积最大值为1.3.
【点睛】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,三角形的面积计算,综合性较强,有一定难度,熟练掌握相关知识是解题的关键,注意分类思想的运用.
24.(1);(2);(3);(4)存在,点的坐标为:或或
【分析】(1)把A、B两点坐标代入可得关于a、b的二元一次方程组,解方程组求出a、b的值即可得答案;
(2)过作轴于,交于,根据抛物线解析式可得点C坐标,利用待定系数法可得直线BC的解析式,设,根据BC解析式可表示出点H坐标,即可表示出DH的长,根据△BCD的面积列方程可求出x的值,即可得点D坐标,利用三角形面积公式即可得答案;
(3)根据二次函数的对称性可得点A与点B关于直线l对称,可得BC为AP+CP的最小值,根据两点间距离公式计算即可得答案;
(4)根据平行四边形的性质得到MB//ND,MB=ND,分MB为边和MB为对角线两种情况,结合点D坐标即可得点N的坐标.
【详解】(1)∵抛物线与轴相交于,两点,,,
∴,
解得:,
∴抛物线的解析式为:.
(2)如图,过作轴于,交于,
当时,,
∴,
设的解析式为,则,
解得,
∴的解析式为:,
设,则,
∴,
∵的面积是,
∴,
∴,
解得:或3,
∵点在直线右侧的抛物线上,
∴,
∴的面积;
(3)∵抛物线与轴相交于,两点,
∴点A与点B关于直线l对称,
∴BC为AP+CP的最小值,
∵B(4,0),C(0,-6),
∴AP+CP的最小值=BC==.
故答案为:
(4)①当MB为对角线时,MN//BD,MN=BD,
过点N作NE⊥x轴于E,过当D作DF⊥x轴于F,
∵点D(3,),
∴DF=,
在△MNE和△BDF中,,
∴△MNE≌△BDF,
∴DF=NE=,
∵点D在x轴下方,MB为对角线,
∴点N在x轴上方,
∴点N纵坐标为,
把y=代入抛物线解析式得:,
解得:,,
∴(,),(,)
如图,当BM为边时,MB//ND,MB=ND,
∵点D(3,),
∴点N纵坐标为,
∴,
解得:,(与点D重合,舍去),
∴(,),
综上所述:存在点,使得以点,,,为顶点的四边形是平行四边形,点的坐标为:或或.
【点睛】本题考查的是二次函数的综合,首先要掌握待定系数法求解析式,其次要添加恰当的辅助线,灵活运用面积公式和平行四边形的判定和性质,应用数形结合的数学思想解题.
数学试卷
考试范围:初中;考试时间:120分钟;满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题只有一个正确答案,每小题3分,满分30分)
1.的倒数的绝对值是( )
A. B. C. D.
2.下列我国四家航空公司的logo图案,中心对称图形是( )
A.B. C.D.
3.下列各式计算正确的是( )
A. B. C. D.
4.一组数据4,5,,7,9的平均数为6,则这组数据的众数为( )
A.4 B.5 C.7 D.9
5.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果,那么的度数是( )
A.22° B.32° C.38° D.44°
6.一个由相同小立方块搭成的几何体,从正面、左面、上面看到的形状图如图所示,则搭成这个几何体的小立方块的个数为( )
A.4个 B.5个 C.6个 D.7个
7.将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A.B.C.D.
8.王芳同学到文具店购买中性笔和笔记本.中性笔每支0.8元,笔记本每本1.2元,王芳带了10元钱,则可供她选择的购买方案的个数为( )(两样都买,余下的钱少于0.8元)
A.6 B.7 C.8 D.9
9.在一个不透明的口袋中装有若干个只有颜色不同的白球和黄球,如果袋中黄球的个数是白球的两倍,那么摸到白球的概率为( )
A. B. C. D.不能确定
10.如图,二次函数()的图象与轴交于A,B两点,与轴交于点C,点A坐标为(-1,0),点C在(0,2)与(0,3)之间(不包括这两点),抛物线的顶点为D,对称轴为直线=2.有以下结论:①;②若点M(,),点N(,)是函数图象上的两点,则;③<<;④不可能是等腰直角三角形.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,满分21分)
11.随着电子技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.00000065m2.这个数用科学记数法表示为_____m2.
12.如图,在平行四边形中,两点均在对角线上.要使四边形为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是__________(写出一个即可).
13.若关于的方程无解,则的值是____________.
14.一个圆锥的侧面展开图的扇形的圆心角为,母线长为12cm,则圆锥的底面半径为_________cm.
15.如图,已知反比例函数y=(k<0)的图象经过Rt△OAB斜边OA的中点D(﹣6,a),且与直角边AB相交于点C.若△AOC的面积为18,则k的值为_____.
16.(2014年江西南昌3分)在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为 .
17.如图,在平面直角坐标系中,将边长为3,4,5的直角△ABO沿x轴向右滚动到的位置,再到的位置…依次进行下去,发现,,…那么点的横坐标为______.
三、解答题(共7道大题,共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)计算:;
(2)因式分解:
19.(本题满分5分)解方程:
20.(本题满分8分)某地区在所有中学开展《老师,我想对你说》心灵信箱活动,为师生之间的沟通增设了一个书面交流的渠道.为了解两年来活动开展的情况,某课题组从全地区随机抽取部分中学生进行问卷调查.对“两年来,你通过心灵信箱给老师总共投递过封信?”这一调查项设有四个回答选项,选项A:没有投过;选项B:一封;选项C:两;选项D:三封及以上.根据接受问卷调查学生的回答,统计出各选项的人数以及所占百分比,分别绘制成如下条形统计图和扇形统计图:
(1)此次抽样调查了 名学生,条形统计图中m= ,n= ;
(2)请将条形统计图补全;
(3)接受问卷调查的学生在活动中投出的信件总数至少有 封;
(4)全地区中学生共有110000名,由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有多少名?
21.(本题满分10分)如图,△ABC中,⊙O经过A、B两点,且交AC于点D,连接BD,∠DBC=∠BAC.
(1)证明BC与⊙O相切;
(2)若⊙O的半径为6,∠BAC=30°,求图中阴影部分的面积.
22.(本题满分10分)已知,两地之间有一条300千米的公路,甲,乙两车同时出发,甲车以60千米/时的速度沿此公路从地匀速开往地,乙车从地沿此公路匀速开往地,两车分别到达目的地后停止,甲,乙两车相距的路程(千米)与甲车的行驶时间(时)之间的函数关系如图所示.
(1)乙车的速度为______千米/时,______,______.
(2)求甲,乙两车相遇后与之间的函数关系式.
(3)当甲车到达距地120千米处时,直接写出甲,乙两车之间的路程.
23.综合与实践(本题满分12分)在数学研究课上,老师出示如图1所示的长方形纸条,,,然后在纸条上任意画一条截线段,将纸片沿折叠,与交于点,得到,如图2所示:
(1)若,求的大小;
(2)改变折痕位置,判断的形状,并说明理由;
(3)爱动脑筋的小明在研究的面积时,发现边上的高始终是个不变的值.根据这一发现,他很快研究出的面积最小值为,求的大小;
(4)小明继续动手操作,发现了面积的最大值,请你求出这个最大值.
24.综合与探究(本题满分14分)如图,抛物线与轴相交于,两点,与轴相交于点,,,直线是抛物线的对称轴,在直线右侧的抛物线上有一动点,连接,,,.
(1)求抛物线的函数表达式:
(2)若点在轴的下方,当的面积是时,求的面积;
(3)在直线上有一点,连接,,则的最小值为______;
(4)在(2)的条件下,点是轴上一点,点是抛物线上一动点,是否存在点,使得以点,,,为顶点的四边形是平行四边形,若存在,请直接写出点的坐标;若不存在,请说明理由.
参考答案:
1.B
【分析】根据题意,要先求出倒数,然后再求绝对值.
【详解】解:的倒数是,的绝对值是.
故选:B .
【点睛】本题考查有理数的倒数和绝对值,熟练掌握倒数和绝对值的计算方法是关键.
2.A
【分析】根据中心对称图形的定义逐一判断即可.
【详解】选项B、C、D都不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形,
选项A能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形,
故选:A
【点睛】本题考查了中心对称图形识别,熟练掌握中心对称图形的定义是解题关键.
3.A
【分析】根据合并同类项法则、完全平方公式、同底数幂的除法和幂的乘方法则进行计算即可.
【详解】解:A. ,计算正确,符合题意;
B. ,原计算错误,不合题意;
C. ,原计算错误,不合题意;
D. ,原计算错误,不合题意,
故选:A.
【点睛】本题考查了合并同类项法则、完全平方公式、同底数幂的除法和幂的乘方法则,熟练掌握各运算法则是解题的关键.
4.B
【分析】先根据平均数的公式计算出x的值,再求这组数据的众数即可.
【详解】解:∵4,5,,7,9的平均数为6,
∴,
解得:x=5,
∴这组数据为:4,5,5,7,9,
∴这组数据的众数为5.
故选:B.
【点睛】本题考查平均数及众数,熟练掌握平均数、众数的意义是解题的关键.
5.C
【分析】根据BE∥CD得到∠EBC=22°,依据∠ABC=60°,∠EBC=22°,由角的和差关系可求∠2=38°.
【详解】解:如图,
∵BE∥CD,
∴∠EBC=∠1=22°,
∵∠ABC=60°,
∴∠2=38°.
故选:C.
【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,内错角相等.
6.B
【分析】从俯视图中可以看出最底层小立方块的个数及形状,从主视图可以看出每一层小立方块的层数和个数,从左视图可看出每一行小立方块的层数和个数,从而算出总的个数.
【详解】解:如图所示,
由俯视图易得:最底层小立方块的个数为4,由其他视图可知第二层有1个小立方块,那么共有个小立方块.
故选:B.
【点睛】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
7.B
【解析】根据将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水,即可求出小水杯内水面的高度h(cm)与注水时间t(min)的函数图象.
解:将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,小玻璃杯内的水原来的高度一定大于0,则可以判断A、D一定错误,用一注水管沿大容器内壁匀速注水,水开始时不会流入小玻璃杯,因而这段时间h不变,当大杯中的水面与小杯水平时,开始向小杯中流水,h随t的增大而增大,当水注满小杯后,小杯内水面的高度h不再变化.
故选B.
8.B
【分析】设购买x支中性笔,y本笔记本,根据题意得出:9.2<0.8x+1.2y≤10,进而求出即可.
【详解】解;设购买x支中性笔,y本笔记本,根据题意得出:
9.2<0.8x+1.2y≤10,
当x=2时,y=7,
当x=3时,y=6,
当x=5时,y=5,
当x=6时,y=4,
当x=8时,y=3,
当x=9时,y=2,
当x=11时,y=1,
故一共有7种方案.
故选:B.
【点睛】此题主要考查了二元一次方程的应用,得出不等关系是解题关键.
9.A
【分析】先设袋中白球的个数为x个,然后根据概率公式列式计算即可.
【详解】解:设袋中白球的个数为x个,则黄球的个数2x,
∴摸到白球的概率==,
故选A.
【点睛】本题考查了概率公式的应用,设出未知数、并运用概率公式列出方程是解答本题的关键.
10.C
【分析】由,得,由点坐标与点坐标得,,由二次函数图象可知,则,得出,故①正确;
点,关于对称轴的对称点为,,,随的增大而增大,则,故②不正确;
由,解得,故③正确;
易求,,则是等腰三角形,如果是等腰直角三角形,则点到的距离等于,则,求出二次函数解析式为,当时,,与点在与之间(不包括这两点)矛盾,得出不可能是等腰直角三角形,故④正确.
【详解】二次函数的对称轴为:,
,
,
点坐标为,点在与之间,且都在抛物线上,
,,
由二次函数图象可知,,
,
又,
,故①正确;
点,关于对称轴的对称点为,,,随的增大而增大,
,故②不正确;
,
解得:,
故③正确;
抛物线的顶点为,对称轴为直线,
点与点关于直线对称,点在直线上,
,,
是等腰三角形,
如果是等腰直角三角形,则点到的距离等于,即,
则,
解得:,
二次函数解析式为:,
当时,,与点在与之间(不包括这两点)矛盾,
不可能是等腰直角三角形,故④正确;
正确的有3个,
故选:C.
【点睛】本题考查二次函数的图象与性质、二次函数解析式的求法、等腰三角形的判定等知识,解题的关键是熟练掌握二次函数的图象与性质,属于中考常考题型.
11.6.5×10﹣7
【详解】试题分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00000065=6.5×10﹣7.
故答案为6.5×10﹣7.
12.(答案不唯一)
【分析】连接BD交AC于点O,由平行四边形的性质可得到OB=OD,要证明四边形BEDF为平行四边形,只需要OE=OF即可,故添加的条件只要能证明OE=OF即可.
【详解】如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
∴OB=OD,OA=OC,
若AE=CF,则有AO-AE=CO-CF,即OE=OF,
∴四边形BEDF为平行四边形,
故答案为:AE=CF.答案不唯一.
【点睛】本题主要考查平行四边形的判定,掌握平行四边形的判定方法是解题的关键.即①两组对边分别平行的四边形是平行四边形,②两组对边分别相等的四边形是平行四边形,③一组对边平行且相等的四边形是平行四边形,④两组对角分别相等的四边形是平行四边形,⑤对角线互相平分的四边形是平行四边形.
13.或
【分析】将分式方程转化为整式方程,分整式方程无解和分式方程有增根两种情况求解即可.
【详解】解:,
方程两边同乘:,得:,
整理得:,
①整式方程无解:,解得:;
②分式方程有增根:或,解得:或;
当时:整式方程无解;
当时:,解得:;
综上,当或时,分式方程无解;
故答案为:或.
【点睛】本题考查分式方程无解问题.熟练掌握整式方程无解或分式方程有增根时,分式方程无解,是解题的关键.
14.
【分析】设圆锥的底面半径为,根据侧面展开图的扇形的弧长等于底面圆的周长,据此作答即可.
【详解】解:设圆锥的底面半径为,
则,
解得:,
故答案为:.
【点睛】考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于侧面展开扇形的弧长,难度不大.
15.-12
【分析】设点A的坐标为(b,c),则点D的坐标为,首先通过点D在反比例函数图像上得出bc=4k,再通过点C在反比例函数图象上得出,然后利用S△AOB﹣S△BOC=S△AOC即可求出k的值.
【详解】设点A的坐标为(b,c),则点D的坐标为(),
∵点D在反比例函数图象上,
∴
化简得:bc=4k,
又∵∠ABO=90°,
点C在反比例函数图象上,
∴,
又∵S△AOB﹣S△BOC=S△AOC,
∴,
解得:k=﹣12,
故答案为:﹣12.
【点睛】本题主要考查反比例函数与几何综合,掌握反比例函数图象上的点满足反比例函数解析式是解题的关键.
16.,或6
【解析】试题分析:根据题意画出图形,分四种情况讨论:
①如答图1:当∠C=60°时,∠ABC=30°,P点在线段AC上,∠ABP不可能等于30°,只能是P点与C点重合,与条件相矛盾.
②如答图2:当∠C=60°时,∠ABC=30°,P点在线段CA的延长上.
∵Rt△ABC中,BC=6,∠C=30°,∴AC=BC=×6=3.
在△ABC和△ABP中,∵∠ABP=∠ABC=30°,AB=AB,∠CAB=∠PAB=90°,
∴△ABC≌△ABP(ASA).∴AC=AP=3.∴CP=AC+AP=3+3=6.
③如图3:当∠ABC=60°时,∠C=30°,P点在线段AC上.
∵Rt△ABC中,BC=6,∠C=30°,∴AB=BC=×6=3.
∵∠ABP=30°,∴AP=BP,∠PBC=∠ABC-∠ABP=60°-30°=30°=∠C.∴PC=PB.
∵在Rt△ABP中, ,∴,解得PB=.
∴PC=PB=.
④如答图4:当∠ABC=60°时,∠C=30°,P点在线段CA的延长线上.
∵∠ABP=30°,∠ABC=60°,∴△PBC是直角三形.
∵∠C=30°,∴PB=PC.
∵在 Rt△PBC中,PC2-PB2=BC2,∴,解得PC=.
综上所述,CP的长为,或6.
考点:1.含30度直角三角形的性质;2.全等三角形的判定和性质;3.勾股定理;4. 分类思想的应用.
17.12135
【分析】根据直角的边长求出点 ,再由沿轴向右滚动到的位置,再到的位置…依次进行下去,即可找到规律,即可求解.
【详解】∵ , , , ,
根据题意知: ,
得:;
继续滚动得:;
发现规律:,
∵ ,解得:
则 ,
∴点的横坐标为,
故答案为:.
【点睛】本题主要考查了规律型:点的坐标,找到规律是解题的关键.
18.(1);(2).
【详解】解:(1)原式 .
(2)
=
=
=
=.
19.【答案】,-3.
【解析】
解:x2+5x+6=0
(x+2)(x+3)=0
x+2=0或x+3=0
,-3.
20.(1)500,225,25;(2)补全图形见解析;(3)425;(4)全地区给老师投过信件的学生约有60500名.
【分析】(1)由B选项人数及其所占百分比求得总人数,再用总人数乘以对应百分比可得m、n的值;
(2)先求出C选项的人数,继而可补全图形;
(3)各选项次数乘以对应人数,再求和即可得;
(4)利用样本估计总体思想求解可得.
【详解】(1)此次调查的总人数为150÷30%=500(人),
则m=500×45%=225,n=500×5%=25,
故答案为500,225,25;
(2)C选项人数为500×20%=100(人),
补全图形如下:
(3)1×150+2×100+3×25=425,
答:接受问卷调查的学生在活动中投出的信件总数至少有425封,
故答案为425;
(4)由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有110000×(1﹣45%)=60500(名).
【点睛】本题考查了条形统计图,扇形统计图,用样本估计总体,准确识图,从中找到必要的信息是解题的关键.
21.(1)证明见解析;(2)6π-9.
【分析】(1)连接BO并延长交⊙O于点E,连接DE.由圆周角定理得出∠BDE=90°,再求出∠EBD+∠DBC=90°,根据切线的判定定理即可得出BC是⊙O的切线;
(2)分别求出等边三角形DOB的面积和扇形DOB的面积,即可求出答案.
【详解】(1)证明:连接BO并延长交⊙O于点E,连接DE,
∵BE是直径,∴∠EDB=90°,
∴∠E+∠EBD=90°
∵=,∴∠E=∠A
又∵∠DBC=∠BAC,∴∠DBC=∠E
∴∠DBC+∠EBD=90°,∴∠EBC=90°,∴BC⊥EB.
又∵OB是半径(B在⊙O上),∴BC与⊙O相切.
(2)∵=,∴∠BOD=2∠A=60°
S阴影= S扇形OBD-S△OBD=π36×-9=6π-9.
【点睛】本题考查了切线的判定,圆周角定理,扇形面积,等边三角形的性质和判定的应用,关键是求出∠EBD+∠DBC=90°和分别求出扇形DOB和三角形DOB的面积.
22.(1)90,,5;(2);(3)150千米.
【分析】(1)根据图象可知2小时后相遇,根据路程和为270千米即可求求出乙车的速度;然后根据路程、速度、时间的关系确定;
(2)运用待定系数法求解即可;
(3)求出甲车到达距地120千米处的时间,带入求解即可;
【详解】(1)乙车的速度为:千米/时,
,
,
故答案为:90,,5.
(2)(千米),
当时,设,
把(2,0),代入;
,
∴,
∴,
当时,设,把点代入可得,
∴,
综上,;
(3)甲车到达距地120千米处的时间为:(小时),
此时的路程为:(千米);
∴甲,乙两车之间的路程150千米.
【点睛】本题主要考查了一次函数的图象应用,准确分析计算是解题的关键.
23.(1)∠MKN=40°;(2)等腰三角形;(3)45°或135°;(4)△MNK的面积最大值为1.3.
【分析】(1)根据矩形的性质和折叠的性质求出∠KNM,∠KMN的度数,根据三角形内角和即可求解;
(2)利用翻折变换的性质以及两直线平行内错角相等得出KM=KN;
(3)利用当△KMN的面积最小值为时,KN=BC=1,故KN⊥B′M,得出∠1=∠NMB=45°,同理当将纸条向下折叠时,∠1=∠NMB=135°;
(4)分情况一:将矩形纸片对折,使点B与D重合,此时点K也与D重合;情况二:将矩形纸片沿对角线AC对折,此时折痕即为AC两种情况讨论求解.
【详解】(1)如图1,
∵四边形ABCD是长方形,
∴AM∥DN,
∴∠KNM=∠1,
∵∠1=70°,
∴∠KNM=∠KMN=∠1=70°,
∴∠MKN=40°;
(2)等腰三角形,理由如下:
∵AM∥BN,∴∠1=∠MND,
∵将纸片沿MN折叠,∴∠1=∠KMN,∠MND=∠KMN,
∴KM=KN,
故的形状是等腰三角形;
(3)如图2,当△KMN的面积最小值为时,KN=BC=1,故KN⊥B′M,
∵∠NMB=∠KMN,∠KMB=90°,
∴∠1=∠NMB=45°,
同理当将纸条向下折叠时,∠1=∠NMB=135°,
所以∠1的度数为45°或135°;
(4)分两种情况:
情况一:如图3,将矩形纸片对折,使点B与D重合,此时点K也与D重合,
MK=MB=x,则AM=5﹣x,
由勾股定理得12+(5﹣x)2=x2,
解得x=2.6,
∴MD=ND=2.6,
S△MNK=S△MND=×1×2.6=1.3;
情况二:如图4,将矩形纸片沿对角线AC对折,此时折痕即为AC,
MK=AK=CK=x,则DK=5﹣x,
同理可得MK=NK=2.6,
∵MD=1,
∴S△MNK=×1×2.6=1.3,
所以△MNK的面积最大值为1.3.
【点睛】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,三角形的面积计算,综合性较强,有一定难度,熟练掌握相关知识是解题的关键,注意分类思想的运用.
24.(1);(2);(3);(4)存在,点的坐标为:或或
【分析】(1)把A、B两点坐标代入可得关于a、b的二元一次方程组,解方程组求出a、b的值即可得答案;
(2)过作轴于,交于,根据抛物线解析式可得点C坐标,利用待定系数法可得直线BC的解析式,设,根据BC解析式可表示出点H坐标,即可表示出DH的长,根据△BCD的面积列方程可求出x的值,即可得点D坐标,利用三角形面积公式即可得答案;
(3)根据二次函数的对称性可得点A与点B关于直线l对称,可得BC为AP+CP的最小值,根据两点间距离公式计算即可得答案;
(4)根据平行四边形的性质得到MB//ND,MB=ND,分MB为边和MB为对角线两种情况,结合点D坐标即可得点N的坐标.
【详解】(1)∵抛物线与轴相交于,两点,,,
∴,
解得:,
∴抛物线的解析式为:.
(2)如图,过作轴于,交于,
当时,,
∴,
设的解析式为,则,
解得,
∴的解析式为:,
设,则,
∴,
∵的面积是,
∴,
∴,
解得:或3,
∵点在直线右侧的抛物线上,
∴,
∴的面积;
(3)∵抛物线与轴相交于,两点,
∴点A与点B关于直线l对称,
∴BC为AP+CP的最小值,
∵B(4,0),C(0,-6),
∴AP+CP的最小值=BC==.
故答案为:
(4)①当MB为对角线时,MN//BD,MN=BD,
过点N作NE⊥x轴于E,过当D作DF⊥x轴于F,
∵点D(3,),
∴DF=,
在△MNE和△BDF中,,
∴△MNE≌△BDF,
∴DF=NE=,
∵点D在x轴下方,MB为对角线,
∴点N在x轴上方,
∴点N纵坐标为,
把y=代入抛物线解析式得:,
解得:,,
∴(,),(,)
如图,当BM为边时,MB//ND,MB=ND,
∵点D(3,),
∴点N纵坐标为,
∴,
解得:,(与点D重合,舍去),
∴(,),
综上所述:存在点,使得以点,,,为顶点的四边形是平行四边形,点的坐标为:或或.
【点睛】本题考查的是二次函数的综合,首先要掌握待定系数法求解析式,其次要添加恰当的辅助线,灵活运用面积公式和平行四边形的判定和性质,应用数形结合的数学思想解题.
同课章节目录
