2024年中考数学总复习验收卷(四)(含解析)
文档属性
| 名称 | 2024年中考数学总复习验收卷(四)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 21:29:02 | ||
图片预览


文档简介
2024年中考数学总复习验收卷(四)
数学试卷
考试范围:初中;考试时间:120分钟;满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题只有一个正确答案,每小题3分,满分30分)
1.已知与4互为相反数,则的倒数是( )
A.4 B. C. D.
2.下列汽车标志中,既是轴对称又是中心对称图形的是( )
A. B. C. D.
3.下列计算正确的是( ).
A. B.
C. D.
4.笔筒中有10支型号、颜色完全相同的铅笔,将它们逐一标上1﹣10的号码,若从笔筒中任意抽出一支铅笔,则抽到编号是3的倍数的概率是( )
A. B. C. D.
5.如图,在中,,,将绕点A逆时针旋转角度()得到.若,则的值为( )
A.65° B.75° C.85° D.95°
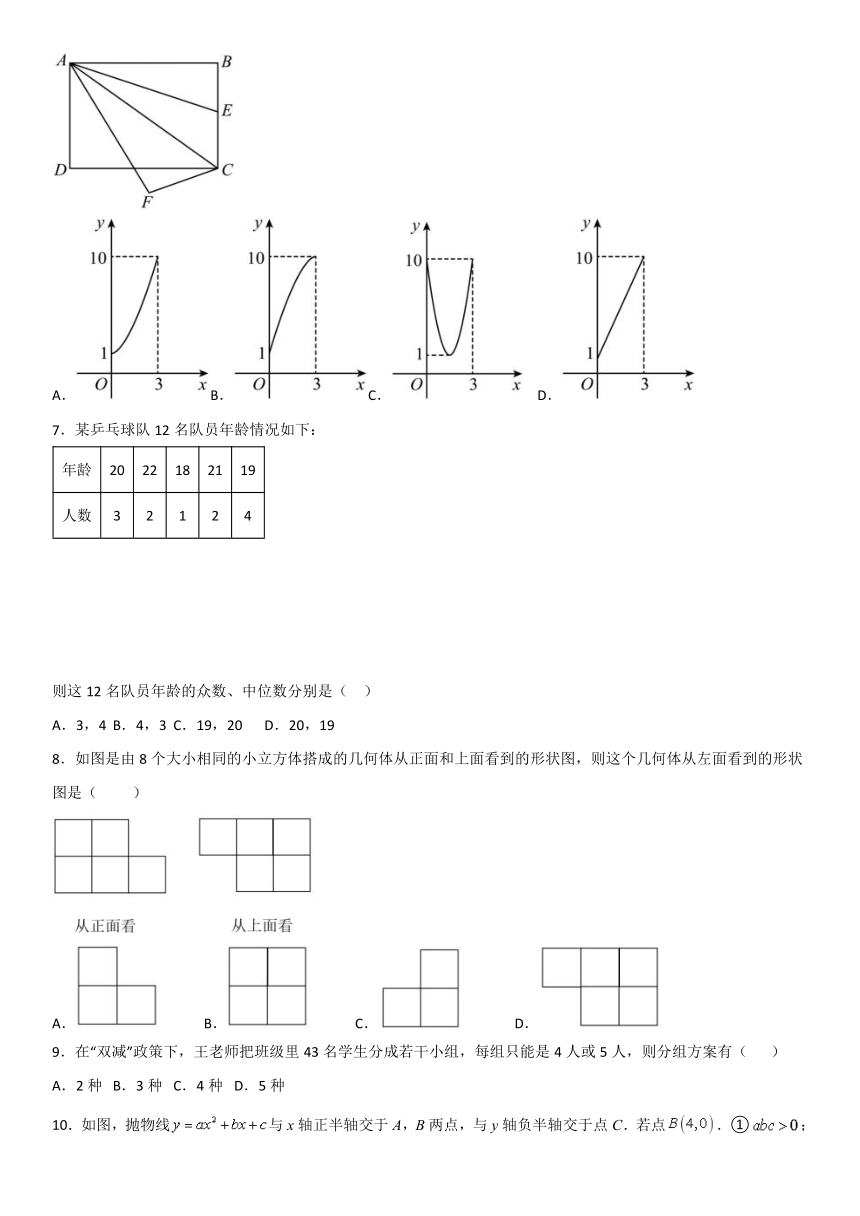
6.如图,矩形中,,点E在边上运动,连接,将绕点A顺时针旋转得到,旋转角等于,连接.设,,则y关于x的函数图象大致为( )
A.B.C. D.
7.某乒乓球队12名队员年龄情况如下:
年龄 20 22 18 21 19
人数 3 2 1 2 4
则这12名队员年龄的众数、中位数分别是( )
A.3,4 B.4,3 C.19,20 D.20,19
8.如图是由8个大小相同的小立方体搭成的几何体从正面和上面看到的形状图,则这个几何体从左面看到的形状图是( )
A. B. C. D.
9.在“双减”政策下,王老师把班级里43名学生分成若干小组,每组只能是4人或5人,则分组方案有( )
A.2种 B.3种 C.4种 D.5种
10.如图,抛物线与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点.①;②;③;④若,则;⑤若抛物线的对称轴是直线,为任意实数,则;则上述结论中,正确的个数是( )
A.5个 B.4个 C.3个 D.2个
二、填空题(每小题3分,满分21分)
11.纳米(nm)是长度单位,1纳米=10-9米,一根头发的直径约为0.048毫米,0.048毫米=_________纳米(用科学记数法表示)
12.函数的自变量的取值范围是______.
13.如图,已知,,点、、、在一条直线上,要使,还需添加一个条件,这个条件可以是___________.
14.若关于的分式方程无解,则的值为 __.
15.在平行四边形ABCD中,AD=10cm,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=4cm,则AB=______cm.
16.如图,直线AB交双曲线于A、B两点,交x轴于点C,且B恰为线段AC的中点,连结OA.若,则k的值为___________.
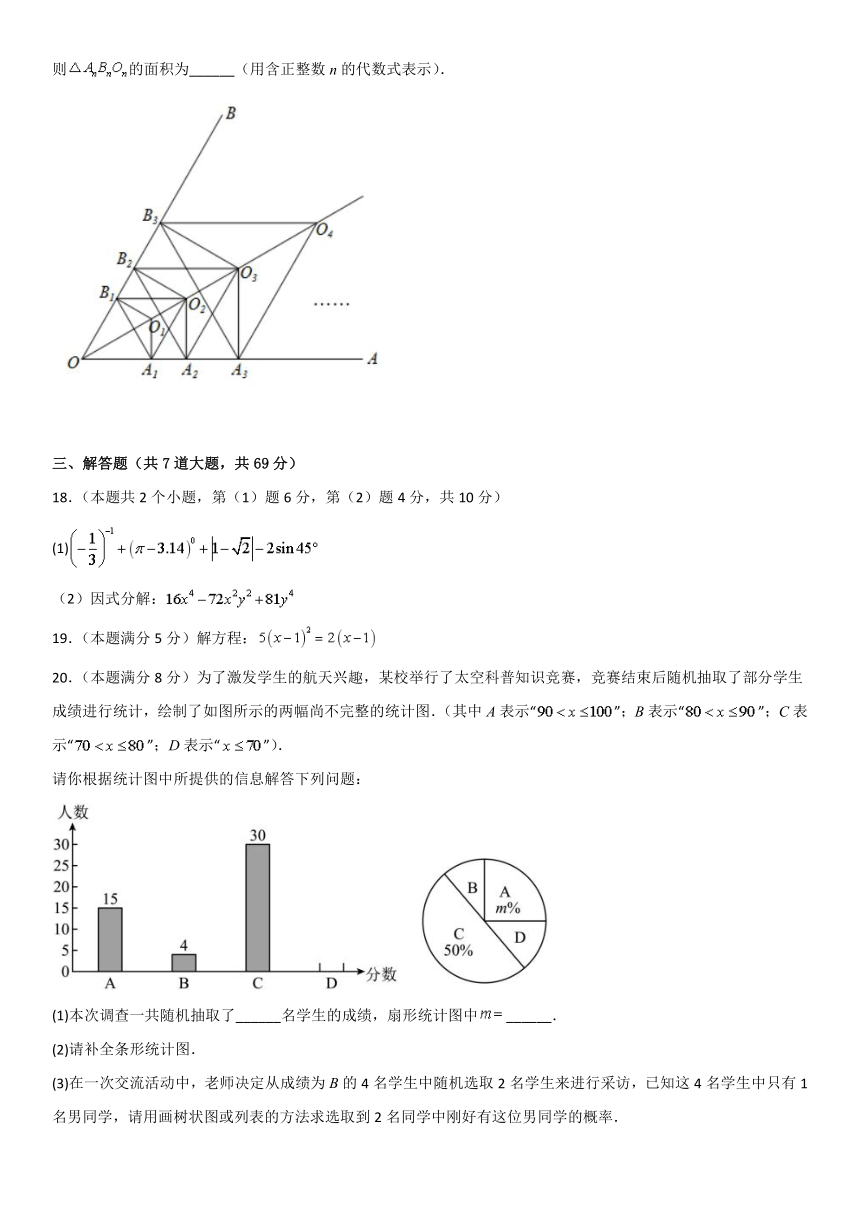
17.如图,,点是平分线上一点,,作,,垂足分别为点,,以为边作等边三角形;作,,垂足分别为点,,以为边作等边三角形;作,,垂足分别为点,,以为边作等边三角形;…按这样的方法继续下去,则的面积为______(用含正整数n的代数式表示).
三、解答题(共7道大题,共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)
(2)因式分解:
19.(本题满分5分)解方程:
20.(本题满分8分)为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,绘制了如图所示的两幅尚不完整的统计图.(其中A表示“”;B表示“”;C表示“”;D表示“”).
请你根据统计图中所提供的信息解答下列问题:
(1)本次调查一共随机抽取了______名学生的成绩,扇形统计图中______.
(2)请补全条形统计图.
(3)在一次交流活动中,老师决定从成绩为B的4名学生中随机选取2名学生来进行采访,已知这4名学生中只有1名男同学,请用画树状图或列表的方法求选取到2名同学中刚好有这位男同学的概率.
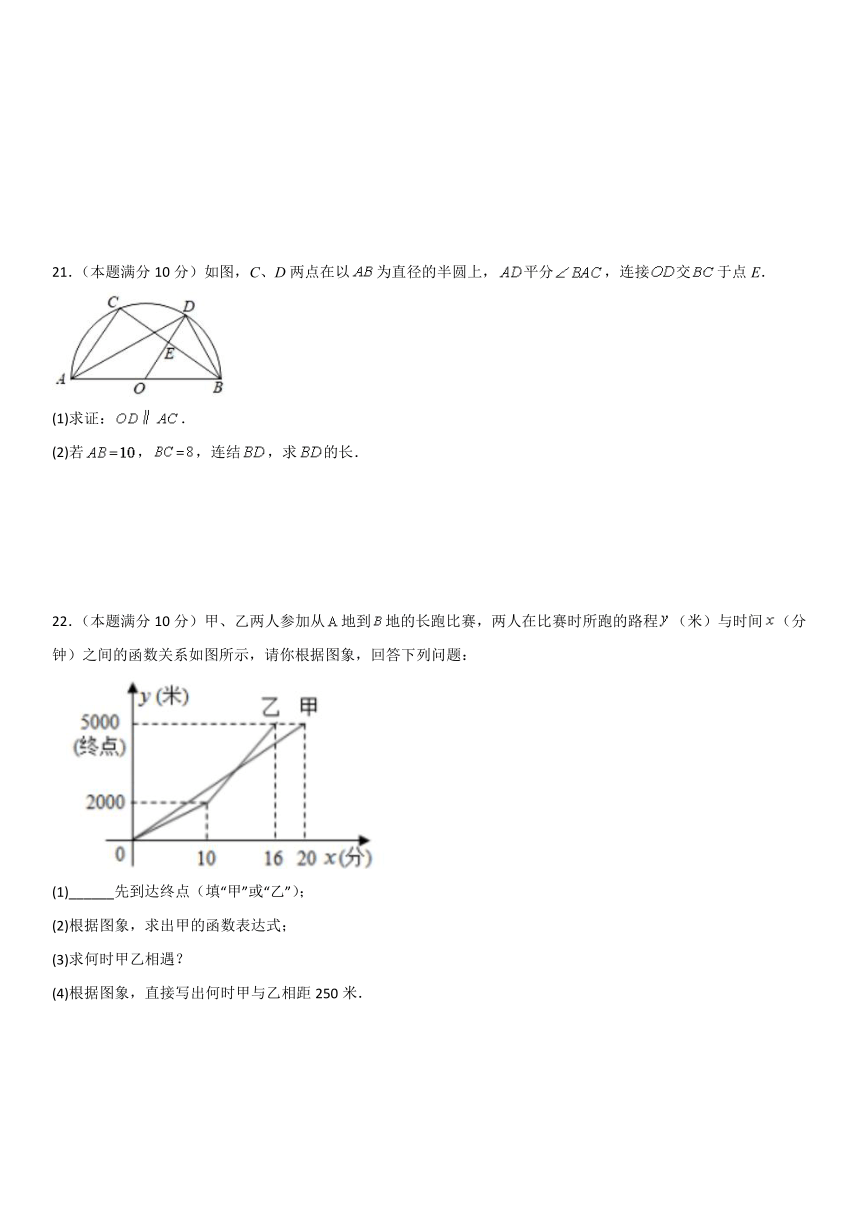
21.(本题满分10分)如图,C、D两点在以为直径的半圆上,平分,连接交于点E.
(1)求证:.
(2)若,,连结,求的长.
22.(本题满分10分)甲、乙两人参加从地到地的长跑比赛,两人在比赛时所跑的路程(米)与时间(分钟)之间的函数关系如图所示,请你根据图象,回答下列问题:
(1)______先到达终点(填“甲”或“乙”);
(2)根据图象,求出甲的函数表达式;
(3)求何时甲乙相遇?
(4)根据图象,直接写出何时甲与乙相距250米.
综合与实践(本题满分12分)
( 定义:长宽比为 ∶1(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图a所示.
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为矩形.
(1)证明:四边形ABCD为矩形;
(2)点M是边AB上一动点.
①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求ON:OM的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求NB:CN的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2,则DR的最小值=
24.综合与探究(本题满分14分)
已知抛物线经过点和点,与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为___________,抛物线的顶点坐标为___________.
(2)如图1,是否存在点P,使四边形的面积为9?若存在,请求出点Р的坐标;若不存在,请说明理由.
(3)如图2,连接交于点,当时,请直接写出点D的坐标;
(4)如图3,点E的坐标为,点C为x轴负半轴上的一点,,连接PE,若,请求出点Р的坐标.
参考答案:
1.D
【分析】根据相反数的含义先求解a,再求解a的倒数即可.
【详解】解:∵与4互为相反数,
∴,
∴的倒数是,
故选D.
【点睛】本题考查的是相反数,倒数的含义,能够正确的求解一个数的相反数与倒数是解本题的关键.
2.D
【分析】根据轴对称、中心对称图形的概念对各选项分析判断后求解.
【详解】解:A.是轴对称,不是中心对称图形,故选项不合题意;
B.不是轴对称,是中心对称图形,故选项不合题意;
C.不是轴对称,也不是中心对称图形,故选项不合题意;
D.是轴对称,也是中心对称图形,故选项符合题意.
故选:D.
【点睛】本题考查了轴对称、中心对称图形,解题的关键是掌握中心对称图形的概念:中心对称图形是要寻找对称中心,旋转后与原图重合.
3.D
【分析】根据,,,即可.
【详解】解:A、,不符合题意;
B、,不符合题意;
C、,不符合题意;
D、,符合题意.
故选:D.
【点睛】本题考查了幂和整式的运算,解题的关键是熟练掌握,,.
4.C
【详解】【分析】由标有1﹣10的号码的10支铅笔中,标号为3的倍数的有3、6、9这3种情况,利用概率公式计算可得.
【详解】∵在标有1﹣10的号码的10支铅笔中,
标号为3的倍数的有3、6、9这3种情况,
∴抽到编号是3的倍数的概率是,
故选C.
【点睛】本题考查了简单的概率计算,用到的知识点为:概率=所求情况数与总情况数之比.
5.B
【分析】由三角形内角和定理可得,根据旋转的性质得出,利用平行线的性质即可得出,即为旋转角.
【详解】解:∵在中,,,
∴,
∵将绕点A逆时针旋转角度()得到,
∴,
∵,
∴,
∴,
∴旋转角的度数是,
故选:B.
【点睛】本题主要考查平行线的性质及旋转的性质,三角形内角和定理,理解题意,找准各角之间的数量关系是解题关键.
6.A
【分析】勾股定理求出,作于M,证明,得到,由此求出,然后根据勾股定理即可得结论.
【详解】解:∵四边形是矩形,
∴,
∵,
∴,
作于M,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
在中,,
∴,
∴,图象对称轴为y轴,开口向上,
当点E与点C重合时,,
∴y关于x的函数图象大致为A,
故选:A.
【点睛】此题考查了动点问题的函数图象,矩形的性质,全等三角形的判定和性质,二次函数的图象和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
7.C
【分析】根据众数定义、中位数的定义及计算方法直接求解即可得到答案.
【详解】解:由年龄统计表可知,这12名队员年龄的众数为;
按照年龄从小到大的顺序可知,18岁1人,19岁4人,20岁3人,因此中位数为;
故选:C.
【点睛】本题考查众数及中位数的定义及计算方法,熟记相关定义并正确分析数据是解决问题的关键.
8.B
【分析】利用俯视图,在相应位置上摆不同的小立方体的个数,使其满足主视图,然后再画出左视图,做出选择.
【详解】解:用从上面看的图形,数字表示该位置上小立方体的个数如下(后面的数量没有8个舍去)
可得左视图为.
故选:B.
【点睛】本题考查了由三视图判断几何体,简单几何体的三视图,把握“长对正,宽相等,高平齐”,利用好俯视图,在相应的位置上摆个数不同的小立方体是常用的方法.
9.A
【分析】设可以分成x组4人组,y组5人组,根据各组的人数之和为43人,即可得出关于x,y的二元一次方程,结合x,y均为自然数,即可得出共有2种分组方案.
【详解】解:设可以分成x组4人组,y组5人组,
依题意得:,
∴.
又∵x,y均为自然数,
∴或,
∴共有2种分组方案.
故选:A.
【点睛】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
10.B
【分析】根据函数的开口,判断a的符号,根据对称轴,判断b的符号,根据于y轴交点,判断c的符号,即可判断①;把点代入得,整理得到,即可判断②;根据该函数图象与x轴的交点个数,即可判断③;根据可得,则当时,,把和分别代入,消去a,即可判断④;根据函数开口向下,对称轴为直线,可知函数的最大值为对应的函数值,则当时,函数值不大于对应的函数值,即可判断⑤.
【详解】解:∵函数开口向下,
∴,
∵函数对称在在y轴左侧,
∴,则,
∵函数图象与y轴相交于负半轴,
∴,
∴,故①正确;
把点代入得:
,
∴,则,
∵,
∴,故②正确;
∵该函数图象与x轴有2个交点,
∴,故③不正确;
∵,
∴,
∵,
∴,
∴当时,,
把代入得:,即
∵,
∴,整理得:,
∵,
∴,故④正确;
把代入得:,
∵抛物线的对称轴是直线,函数图象开口向下,
∴该函数的顶点坐标为:,即该函数最大值为,
当时,,
∴,
整理得:,即,故⑤正确;
综上:正确的有①②④⑤,共4个;
故选:B.
【点睛】本题主要考查了二次函数的图象和性质,解题的关键是熟练掌握二次函数的图象和系数的关系.
11.4.8
【分析】先把毫米换算成米,再根据1纳米=10-9米得出1米=109纳米,利用同底数幂的乘法运算,结合科学记数法的表示方法即可求解.
【详解】解:0.048毫米=0.048×米=4.8××米=4.8米,
∵1纳米=10-9米,
∴1米=109纳米,
∴0.048毫米=4.8米=4.8×109纳米=4.8纳米.
故答案为:4.8.
【点睛】本题考查用科学记数法,长度单位的换算,同底数幂的乘法运算,熟练掌握科学记数法的表示方法是解题关键.
12.且
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,可以求出x的范围.
【详解】解:根据题意得:,
解得:且.
故答案为:且.
【点睛】本题考查了函数自变量的范围的求法,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.
13.(答案不唯一)
【分析】要判定,已知,,则,具备了一组角和一组边对应相等,故可以添加,利用可证全等.
【详解】解:增加一个条件:,
∵,
∴.
∵,
∴,即,
∴,
故答案为:(答案不唯一).
【点睛】本题考查了全等三角形的判定;判定方法有、、、等,在选择时要结合其它已知在图形上的位置进行选取.
14.10或或3
【分析】分式方程无解的情况有两种:(1)原方程存在增根;(2)原方程约去分母后,整式方程无解.
【详解】解:(1)为原方程的增根,
此时有,即,
解得;
(2)为原方程的增根,
此时有,即,
解得.
(3)方程两边都乘,
得,
化简得:.
当时,整式方程无解.
综上所述,当或或时,原方程无解.
故答案为:10或或3.
【点睛】本题考查的是分式方程的解,解答此类题目既要考虑分式方程有增根的情形,又要考虑整式方程无解的情形.
15.7或3
【分析】根据平行线的性质得到∠ADF=∠DFC,由DF平分∠ADC,得到∠ADF=∠CDF,等量代换得到∠DFC=∠FDC,根据等腰三角形的判定得到CF=CD,同理BE=AB,根据已知条件得到四边形ABCD是平行四边形,根据平行四边形的性质得到AB=CD,AD=BC,即可得到结论.
【详解】①如图1,
在 ABCD中,∵ADBC,
∴∠ADF=∠DFC,
∵DF平分∠ADC,
∴∠ADF=∠CDF,
∴∠DFC=∠FDC,
∴CF=CD,
同理BE=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴AB=BE=CF=CD,
∵BC=BE+CF-EF=10cm,
∴BE=CF=7cm,即AB=7cm.
②如图2,
在 ABCD中,∵ADBC,
∴∠ADF=∠DFC,
∵DF平分∠ADC,
∴∠ADF=∠CDF,
∴∠DFC=∠FDC,
∴CF=CD,
同理BE=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴AB=BE=CF=CD,
∵BC=BE+CF+EF=10cm,
∴BE=CF=3cm,即AB=3cm;
综上所述:AB的长为7cm或3cm.
故答案为:7或3.
【点睛】本题考查了等腰三角形的判定和性质,平行四边形的性质,解答本题的关键是判断出BA=BE=CF=CD.
16.
【分析】设A点坐标为(a,),C点坐标为(b,0),根据线段中点坐标公式得到B点坐标为(,),利用反比例函数图象上点的坐标特征得到 k,得到b=3a,
然后根据三角形面积公式得到b ,于是可计算出k的值.
【详解】设A点坐标为(a,),C点坐标为(b,0).
∵B恰为线段AC的中点,∴B点坐标为(,).
∵B点在反比例函数图象上,∴ k,∴b=3a.
∵S△OAC=,∴b ,∴ 3a ,∴k=.
故答案为:.
【点睛】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数解析式.
17.
【分析】设A1B1,A2B2,A3B3与角平分线的交点为C1,C2,C3,根据等边三角形的判定和性质求得OC1,可得△A1B1O1面积,由△A1B1O1∽△A2B2C2,求得相似比OA1∶OA2,可得面积比;同理可得△A3B3C3面积,…,△AnBnOn面积;
【详解】解:如图,设A1B1,A2B2,A3B3与角平分线的交点为C1,C2,C3,
∵∠O1OA1=∠O1OB1=30°,O1A1⊥OA,O1B1⊥OB,OO1=2,
∴OA1=OB1=OO1cos30°=,
∠AOB=60°,则△OA1B1是等边三角形,
∵OO3平分∠AOB,
∴OO1⊥A1B1,OC1=OA1cos30°=,
∴O1C1=2-=,
∴△A1B1O1面积=A1B1 O1C1=,
△O2A1B1是等边三角形,O2A1=A1B1=OA1=,O2O⊥A1B1,则O2C1=O2A1 cos30°=,
∴O2O= OC1+ O2C1=3,
∴OA2=OO2 cos30°=,
△A1B1O1中,∠O1A1B1=∠O1A1O-∠B1A1O=30°,∠O1B1A1=∠O1B1O-∠A1B1O=30°,
OA2=OB2=OO2cos30°,∠AOB=60°,则△OA2B2是等边三角形,
△A2B2O2中,∠O2A2B2=∠O2A2O-∠B2A2O=30°,∠O2B2A2=∠O2B2O-∠A2B2O=30°,
∴△A1B1O1∽△A2B2O2,
相似比为A1B1∶A2B2= OA1∶OA2=∶=2∶3,
∴△A1B1O1和△A2B2C2面积比为4∶9,
△A2B2C2面积=×,
同理可得△A2B2O2和△A3B3C3面积比为4∶9,
△A3B3C3面积=△A2B2C2面积=×,
…,
△AnBnOn面积=×=,
故答案为:;
【点睛】本题考查了等边三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识;掌握相似三角形的性质是解题关键.
18.(1);
(2).
【详解】(1)解:
;
(2)解:
19.,.
【详解】解:
或
,.
20.(1)60;25
(2)详见解析
(3)
【分析】(1)由C组的人数除以所占百分比得出本次调查一共随机抽取的学生人数,用A组人数除以本次调查一共随机抽取的学生人数即可得到m的值;
(2)求出D组的人数,补全学生成绩人数条形统计图即可;
(3)画树状图,共有12种等可能结果,其中刚好有这位男同学的结果数为6,再由概率公式求解即可.
【详解】(1)解:一共随机抽取的学生人数:(名)
;
(2)解:(名),
补全条形统计图如下.
(3)解:设成绩为B的四名学生分别用女1、女2、女3、男表示,画出的树状图如下:
共有12种等可能结果,其中刚好有这位男同学的结果数为6,
∴选取到两名同学中,刚好有这位男同学的概率为.
【点睛】本题考查了用树状图法求概率以及条形统计图和扇形统计图等知识,解题的关键是明确条形统计图和扇形统计图求总人数的方法,画树状图要不重复不遗漏的列出所有可能的结果.
21.(1)见解析
(2)
【分析】(1)根据角平分线的定义得出,根据等腰三角形的性质得出,求出,再根据平行线的判定得出即可;
(2)根据圆周角定理得出,根据平行线的性质得出,根据勾股定理求出,根据三角形的中位线求出,求出,根据相似求出,再根据勾股定理求出,再根据勾股定理求出即可.
【详解】(1)证明:平分,
,
,
,
,
;
(2)解:设交于,
是的直径,
,
,
,
由勾股定理得:,
,,
,
,
,
,
,
,
,
,
,
解得:,则,
在中,由勾股定理得:,
在中,由勾股定理得:.
【点睛】本题考查了平行线的性质和判定,圆周角定理,等腰三角形的性质,三角形的中位线,相似三角形的性质和判定,勾股定理等知识点,能求出长和是解此题的关键,综合性比较强.
22.(1)乙
(2)甲的表达式为:
(3)甲乙在12分钟时相遇
(4)5分钟或11分钟或13分钟或19分钟时甲乙相距250米
【分析】(1)依据函数图象可得到两人跑完全程所用的时间,从而可知道谁先到达终点;
(2)甲的函数图象是正比例函数,直线经过点,可求出解析式;
(3)当时,甲乙两人相遇,求得乙的路程与时间的函数关系式,再求得两个函数图象的交点坐标即可;
(4)根据题意列方程解答即可.
【详解】(1)解:由函数图象可以:甲跑完全程需要20分钟,乙跑完全程需要16分钟,所以乙先到达终点,
故答案为:乙;
(2)解:设甲跑的路程(米)与时间(分钟)之间的函数关系式为:,经过点,
,解得:,
甲的函数解析式为:;
(3)解:设甲乙相遇后(即),乙跑的路程(米)与时间(分钟)之间的函数关系式为:,经过点,,联立方程可得:
,解得,
乙的函数解析式为:,
再联立方程:,解得,
甲乙在12分钟时相遇;
(4)解:设此时起跑了分钟,
根据题意得,或或或,
解得:或或或,
5分钟或11分钟或13分钟或19分钟时甲乙相距250米.
【点睛】本题主要考查了一次函数的应用,求得甲乙两人的路程与时间的函数关系式是解题的关键.
23.(1)见解析
(2)①;②;③2
【分析】(1)设正方形的边长为,先根据折叠的性质证四边形是矩形,再根据是等腰直角三角形得出和的比例关系,即可得证结论;
(2)①作,,垂足分别为,,证,根据线段比例关系得出即可得出结论;
②作点关于直线的对称点,连接交于点,连接,此时周长最小,根据平行线分线段成比例求出此时线段的比值即可;
③根据题意得出点在以为直径的圆上,根据勾股定理求出的最小值即可.
【详解】(1)证明:设正方形的边长为,
是正方形的对角线,
,
由折叠的性质可知,
,
四边形的矩形,
是等腰直角三角形,
,
,
四边形是矩形;
(2)解:①如图,作,,垂足分别为,,
四边形是矩形,,
四边形是矩形,
,,,
,,
为的中点,
,,
,
,
,
,
;
②作点关于直线的对称点,连接交于点,连接,
此时最小等于,
则此时的周长最小,
,
,
设,则,
,
;
即
③四边形是矩形,,
,
,
点在以为直径的圆上,即的中点为,
,
最小,
故答案为:2.
【点睛】本题主要考查四边形的综合知识,解题的关键是熟练掌握矩形的性质,明确矩形的定义及掌握平行线分线段成比例、相似三角形的判定和性质等知识.
24.(1);;
(2)不存在满足条件的点
(3)
(4),
【分析】(1)设函数的表达式为:,即可求解;
(2)利用,即可求解;
(3),则,即可求解;
(4),,则,故,即可求解.
【详解】(1)解:设函数的表达式为:,
即:,
解得:.
故抛物线的表达式为:.
顶点坐标为;
故答案是:;;
(2)不存在,理由:
如答图1,连接,过点作轴的平行线交于点,
由题意得:,
∴直线的表达式为:,
设点,点,
则,
整理得:,
解得:,故方程无解,
则不存在满足条件的点;
(3)∵,
,
过作于,
,
,
∴
∴
∴点;
(4)如答图2,设直线交轴于点,
,,
,
,
则直线的表达式为:,
联立方程,得
解得:(舍去正值),
故点,.
【点睛】本题考查的是二次函数综合运用,涉及到一次函数、一元二次方程应用、图形的面积计算,掌握函数图像上点的坐标特征,待定系数法是关键.
数学试卷
考试范围:初中;考试时间:120分钟;满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题只有一个正确答案,每小题3分,满分30分)
1.已知与4互为相反数,则的倒数是( )
A.4 B. C. D.
2.下列汽车标志中,既是轴对称又是中心对称图形的是( )
A. B. C. D.
3.下列计算正确的是( ).
A. B.
C. D.
4.笔筒中有10支型号、颜色完全相同的铅笔,将它们逐一标上1﹣10的号码,若从笔筒中任意抽出一支铅笔,则抽到编号是3的倍数的概率是( )
A. B. C. D.
5.如图,在中,,,将绕点A逆时针旋转角度()得到.若,则的值为( )
A.65° B.75° C.85° D.95°
6.如图,矩形中,,点E在边上运动,连接,将绕点A顺时针旋转得到,旋转角等于,连接.设,,则y关于x的函数图象大致为( )
A.B.C. D.
7.某乒乓球队12名队员年龄情况如下:
年龄 20 22 18 21 19
人数 3 2 1 2 4
则这12名队员年龄的众数、中位数分别是( )
A.3,4 B.4,3 C.19,20 D.20,19
8.如图是由8个大小相同的小立方体搭成的几何体从正面和上面看到的形状图,则这个几何体从左面看到的形状图是( )
A. B. C. D.
9.在“双减”政策下,王老师把班级里43名学生分成若干小组,每组只能是4人或5人,则分组方案有( )
A.2种 B.3种 C.4种 D.5种
10.如图,抛物线与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点.①;②;③;④若,则;⑤若抛物线的对称轴是直线,为任意实数,则;则上述结论中,正确的个数是( )
A.5个 B.4个 C.3个 D.2个
二、填空题(每小题3分,满分21分)
11.纳米(nm)是长度单位,1纳米=10-9米,一根头发的直径约为0.048毫米,0.048毫米=_________纳米(用科学记数法表示)
12.函数的自变量的取值范围是______.
13.如图,已知,,点、、、在一条直线上,要使,还需添加一个条件,这个条件可以是___________.
14.若关于的分式方程无解,则的值为 __.
15.在平行四边形ABCD中,AD=10cm,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=4cm,则AB=______cm.
16.如图,直线AB交双曲线于A、B两点,交x轴于点C,且B恰为线段AC的中点,连结OA.若,则k的值为___________.
17.如图,,点是平分线上一点,,作,,垂足分别为点,,以为边作等边三角形;作,,垂足分别为点,,以为边作等边三角形;作,,垂足分别为点,,以为边作等边三角形;…按这样的方法继续下去,则的面积为______(用含正整数n的代数式表示).
三、解答题(共7道大题,共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)
(2)因式分解:
19.(本题满分5分)解方程:
20.(本题满分8分)为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,绘制了如图所示的两幅尚不完整的统计图.(其中A表示“”;B表示“”;C表示“”;D表示“”).
请你根据统计图中所提供的信息解答下列问题:
(1)本次调查一共随机抽取了______名学生的成绩,扇形统计图中______.
(2)请补全条形统计图.
(3)在一次交流活动中,老师决定从成绩为B的4名学生中随机选取2名学生来进行采访,已知这4名学生中只有1名男同学,请用画树状图或列表的方法求选取到2名同学中刚好有这位男同学的概率.
21.(本题满分10分)如图,C、D两点在以为直径的半圆上,平分,连接交于点E.
(1)求证:.
(2)若,,连结,求的长.
22.(本题满分10分)甲、乙两人参加从地到地的长跑比赛,两人在比赛时所跑的路程(米)与时间(分钟)之间的函数关系如图所示,请你根据图象,回答下列问题:
(1)______先到达终点(填“甲”或“乙”);
(2)根据图象,求出甲的函数表达式;
(3)求何时甲乙相遇?
(4)根据图象,直接写出何时甲与乙相距250米.
综合与实践(本题满分12分)
( 定义:长宽比为 ∶1(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图a所示.
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为矩形.
(1)证明:四边形ABCD为矩形;
(2)点M是边AB上一动点.
①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求ON:OM的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求NB:CN的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2,则DR的最小值=
24.综合与探究(本题满分14分)
已知抛物线经过点和点,与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为___________,抛物线的顶点坐标为___________.
(2)如图1,是否存在点P,使四边形的面积为9?若存在,请求出点Р的坐标;若不存在,请说明理由.
(3)如图2,连接交于点,当时,请直接写出点D的坐标;
(4)如图3,点E的坐标为,点C为x轴负半轴上的一点,,连接PE,若,请求出点Р的坐标.
参考答案:
1.D
【分析】根据相反数的含义先求解a,再求解a的倒数即可.
【详解】解:∵与4互为相反数,
∴,
∴的倒数是,
故选D.
【点睛】本题考查的是相反数,倒数的含义,能够正确的求解一个数的相反数与倒数是解本题的关键.
2.D
【分析】根据轴对称、中心对称图形的概念对各选项分析判断后求解.
【详解】解:A.是轴对称,不是中心对称图形,故选项不合题意;
B.不是轴对称,是中心对称图形,故选项不合题意;
C.不是轴对称,也不是中心对称图形,故选项不合题意;
D.是轴对称,也是中心对称图形,故选项符合题意.
故选:D.
【点睛】本题考查了轴对称、中心对称图形,解题的关键是掌握中心对称图形的概念:中心对称图形是要寻找对称中心,旋转后与原图重合.
3.D
【分析】根据,,,即可.
【详解】解:A、,不符合题意;
B、,不符合题意;
C、,不符合题意;
D、,符合题意.
故选:D.
【点睛】本题考查了幂和整式的运算,解题的关键是熟练掌握,,.
4.C
【详解】【分析】由标有1﹣10的号码的10支铅笔中,标号为3的倍数的有3、6、9这3种情况,利用概率公式计算可得.
【详解】∵在标有1﹣10的号码的10支铅笔中,
标号为3的倍数的有3、6、9这3种情况,
∴抽到编号是3的倍数的概率是,
故选C.
【点睛】本题考查了简单的概率计算,用到的知识点为:概率=所求情况数与总情况数之比.
5.B
【分析】由三角形内角和定理可得,根据旋转的性质得出,利用平行线的性质即可得出,即为旋转角.
【详解】解:∵在中,,,
∴,
∵将绕点A逆时针旋转角度()得到,
∴,
∵,
∴,
∴,
∴旋转角的度数是,
故选:B.
【点睛】本题主要考查平行线的性质及旋转的性质,三角形内角和定理,理解题意,找准各角之间的数量关系是解题关键.
6.A
【分析】勾股定理求出,作于M,证明,得到,由此求出,然后根据勾股定理即可得结论.
【详解】解:∵四边形是矩形,
∴,
∵,
∴,
作于M,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
在中,,
∴,
∴,图象对称轴为y轴,开口向上,
当点E与点C重合时,,
∴y关于x的函数图象大致为A,
故选:A.
【点睛】此题考查了动点问题的函数图象,矩形的性质,全等三角形的判定和性质,二次函数的图象和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
7.C
【分析】根据众数定义、中位数的定义及计算方法直接求解即可得到答案.
【详解】解:由年龄统计表可知,这12名队员年龄的众数为;
按照年龄从小到大的顺序可知,18岁1人,19岁4人,20岁3人,因此中位数为;
故选:C.
【点睛】本题考查众数及中位数的定义及计算方法,熟记相关定义并正确分析数据是解决问题的关键.
8.B
【分析】利用俯视图,在相应位置上摆不同的小立方体的个数,使其满足主视图,然后再画出左视图,做出选择.
【详解】解:用从上面看的图形,数字表示该位置上小立方体的个数如下(后面的数量没有8个舍去)
可得左视图为.
故选:B.
【点睛】本题考查了由三视图判断几何体,简单几何体的三视图,把握“长对正,宽相等,高平齐”,利用好俯视图,在相应的位置上摆个数不同的小立方体是常用的方法.
9.A
【分析】设可以分成x组4人组,y组5人组,根据各组的人数之和为43人,即可得出关于x,y的二元一次方程,结合x,y均为自然数,即可得出共有2种分组方案.
【详解】解:设可以分成x组4人组,y组5人组,
依题意得:,
∴.
又∵x,y均为自然数,
∴或,
∴共有2种分组方案.
故选:A.
【点睛】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
10.B
【分析】根据函数的开口,判断a的符号,根据对称轴,判断b的符号,根据于y轴交点,判断c的符号,即可判断①;把点代入得,整理得到,即可判断②;根据该函数图象与x轴的交点个数,即可判断③;根据可得,则当时,,把和分别代入,消去a,即可判断④;根据函数开口向下,对称轴为直线,可知函数的最大值为对应的函数值,则当时,函数值不大于对应的函数值,即可判断⑤.
【详解】解:∵函数开口向下,
∴,
∵函数对称在在y轴左侧,
∴,则,
∵函数图象与y轴相交于负半轴,
∴,
∴,故①正确;
把点代入得:
,
∴,则,
∵,
∴,故②正确;
∵该函数图象与x轴有2个交点,
∴,故③不正确;
∵,
∴,
∵,
∴,
∴当时,,
把代入得:,即
∵,
∴,整理得:,
∵,
∴,故④正确;
把代入得:,
∵抛物线的对称轴是直线,函数图象开口向下,
∴该函数的顶点坐标为:,即该函数最大值为,
当时,,
∴,
整理得:,即,故⑤正确;
综上:正确的有①②④⑤,共4个;
故选:B.
【点睛】本题主要考查了二次函数的图象和性质,解题的关键是熟练掌握二次函数的图象和系数的关系.
11.4.8
【分析】先把毫米换算成米,再根据1纳米=10-9米得出1米=109纳米,利用同底数幂的乘法运算,结合科学记数法的表示方法即可求解.
【详解】解:0.048毫米=0.048×米=4.8××米=4.8米,
∵1纳米=10-9米,
∴1米=109纳米,
∴0.048毫米=4.8米=4.8×109纳米=4.8纳米.
故答案为:4.8.
【点睛】本题考查用科学记数法,长度单位的换算,同底数幂的乘法运算,熟练掌握科学记数法的表示方法是解题关键.
12.且
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,可以求出x的范围.
【详解】解:根据题意得:,
解得:且.
故答案为:且.
【点睛】本题考查了函数自变量的范围的求法,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.
13.(答案不唯一)
【分析】要判定,已知,,则,具备了一组角和一组边对应相等,故可以添加,利用可证全等.
【详解】解:增加一个条件:,
∵,
∴.
∵,
∴,即,
∴,
故答案为:(答案不唯一).
【点睛】本题考查了全等三角形的判定;判定方法有、、、等,在选择时要结合其它已知在图形上的位置进行选取.
14.10或或3
【分析】分式方程无解的情况有两种:(1)原方程存在增根;(2)原方程约去分母后,整式方程无解.
【详解】解:(1)为原方程的增根,
此时有,即,
解得;
(2)为原方程的增根,
此时有,即,
解得.
(3)方程两边都乘,
得,
化简得:.
当时,整式方程无解.
综上所述,当或或时,原方程无解.
故答案为:10或或3.
【点睛】本题考查的是分式方程的解,解答此类题目既要考虑分式方程有增根的情形,又要考虑整式方程无解的情形.
15.7或3
【分析】根据平行线的性质得到∠ADF=∠DFC,由DF平分∠ADC,得到∠ADF=∠CDF,等量代换得到∠DFC=∠FDC,根据等腰三角形的判定得到CF=CD,同理BE=AB,根据已知条件得到四边形ABCD是平行四边形,根据平行四边形的性质得到AB=CD,AD=BC,即可得到结论.
【详解】①如图1,
在 ABCD中,∵ADBC,
∴∠ADF=∠DFC,
∵DF平分∠ADC,
∴∠ADF=∠CDF,
∴∠DFC=∠FDC,
∴CF=CD,
同理BE=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴AB=BE=CF=CD,
∵BC=BE+CF-EF=10cm,
∴BE=CF=7cm,即AB=7cm.
②如图2,
在 ABCD中,∵ADBC,
∴∠ADF=∠DFC,
∵DF平分∠ADC,
∴∠ADF=∠CDF,
∴∠DFC=∠FDC,
∴CF=CD,
同理BE=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴AB=BE=CF=CD,
∵BC=BE+CF+EF=10cm,
∴BE=CF=3cm,即AB=3cm;
综上所述:AB的长为7cm或3cm.
故答案为:7或3.
【点睛】本题考查了等腰三角形的判定和性质,平行四边形的性质,解答本题的关键是判断出BA=BE=CF=CD.
16.
【分析】设A点坐标为(a,),C点坐标为(b,0),根据线段中点坐标公式得到B点坐标为(,),利用反比例函数图象上点的坐标特征得到 k,得到b=3a,
然后根据三角形面积公式得到b ,于是可计算出k的值.
【详解】设A点坐标为(a,),C点坐标为(b,0).
∵B恰为线段AC的中点,∴B点坐标为(,).
∵B点在反比例函数图象上,∴ k,∴b=3a.
∵S△OAC=,∴b ,∴ 3a ,∴k=.
故答案为:.
【点睛】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数解析式.
17.
【分析】设A1B1,A2B2,A3B3与角平分线的交点为C1,C2,C3,根据等边三角形的判定和性质求得OC1,可得△A1B1O1面积,由△A1B1O1∽△A2B2C2,求得相似比OA1∶OA2,可得面积比;同理可得△A3B3C3面积,…,△AnBnOn面积;
【详解】解:如图,设A1B1,A2B2,A3B3与角平分线的交点为C1,C2,C3,
∵∠O1OA1=∠O1OB1=30°,O1A1⊥OA,O1B1⊥OB,OO1=2,
∴OA1=OB1=OO1cos30°=,
∠AOB=60°,则△OA1B1是等边三角形,
∵OO3平分∠AOB,
∴OO1⊥A1B1,OC1=OA1cos30°=,
∴O1C1=2-=,
∴△A1B1O1面积=A1B1 O1C1=,
△O2A1B1是等边三角形,O2A1=A1B1=OA1=,O2O⊥A1B1,则O2C1=O2A1 cos30°=,
∴O2O= OC1+ O2C1=3,
∴OA2=OO2 cos30°=,
△A1B1O1中,∠O1A1B1=∠O1A1O-∠B1A1O=30°,∠O1B1A1=∠O1B1O-∠A1B1O=30°,
OA2=OB2=OO2cos30°,∠AOB=60°,则△OA2B2是等边三角形,
△A2B2O2中,∠O2A2B2=∠O2A2O-∠B2A2O=30°,∠O2B2A2=∠O2B2O-∠A2B2O=30°,
∴△A1B1O1∽△A2B2O2,
相似比为A1B1∶A2B2= OA1∶OA2=∶=2∶3,
∴△A1B1O1和△A2B2C2面积比为4∶9,
△A2B2C2面积=×,
同理可得△A2B2O2和△A3B3C3面积比为4∶9,
△A3B3C3面积=△A2B2C2面积=×,
…,
△AnBnOn面积=×=,
故答案为:;
【点睛】本题考查了等边三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识;掌握相似三角形的性质是解题关键.
18.(1);
(2).
【详解】(1)解:
;
(2)解:
19.,.
【详解】解:
或
,.
20.(1)60;25
(2)详见解析
(3)
【分析】(1)由C组的人数除以所占百分比得出本次调查一共随机抽取的学生人数,用A组人数除以本次调查一共随机抽取的学生人数即可得到m的值;
(2)求出D组的人数,补全学生成绩人数条形统计图即可;
(3)画树状图,共有12种等可能结果,其中刚好有这位男同学的结果数为6,再由概率公式求解即可.
【详解】(1)解:一共随机抽取的学生人数:(名)
;
(2)解:(名),
补全条形统计图如下.
(3)解:设成绩为B的四名学生分别用女1、女2、女3、男表示,画出的树状图如下:
共有12种等可能结果,其中刚好有这位男同学的结果数为6,
∴选取到两名同学中,刚好有这位男同学的概率为.
【点睛】本题考查了用树状图法求概率以及条形统计图和扇形统计图等知识,解题的关键是明确条形统计图和扇形统计图求总人数的方法,画树状图要不重复不遗漏的列出所有可能的结果.
21.(1)见解析
(2)
【分析】(1)根据角平分线的定义得出,根据等腰三角形的性质得出,求出,再根据平行线的判定得出即可;
(2)根据圆周角定理得出,根据平行线的性质得出,根据勾股定理求出,根据三角形的中位线求出,求出,根据相似求出,再根据勾股定理求出,再根据勾股定理求出即可.
【详解】(1)证明:平分,
,
,
,
,
;
(2)解:设交于,
是的直径,
,
,
,
由勾股定理得:,
,,
,
,
,
,
,
,
,
,
,
解得:,则,
在中,由勾股定理得:,
在中,由勾股定理得:.
【点睛】本题考查了平行线的性质和判定,圆周角定理,等腰三角形的性质,三角形的中位线,相似三角形的性质和判定,勾股定理等知识点,能求出长和是解此题的关键,综合性比较强.
22.(1)乙
(2)甲的表达式为:
(3)甲乙在12分钟时相遇
(4)5分钟或11分钟或13分钟或19分钟时甲乙相距250米
【分析】(1)依据函数图象可得到两人跑完全程所用的时间,从而可知道谁先到达终点;
(2)甲的函数图象是正比例函数,直线经过点,可求出解析式;
(3)当时,甲乙两人相遇,求得乙的路程与时间的函数关系式,再求得两个函数图象的交点坐标即可;
(4)根据题意列方程解答即可.
【详解】(1)解:由函数图象可以:甲跑完全程需要20分钟,乙跑完全程需要16分钟,所以乙先到达终点,
故答案为:乙;
(2)解:设甲跑的路程(米)与时间(分钟)之间的函数关系式为:,经过点,
,解得:,
甲的函数解析式为:;
(3)解:设甲乙相遇后(即),乙跑的路程(米)与时间(分钟)之间的函数关系式为:,经过点,,联立方程可得:
,解得,
乙的函数解析式为:,
再联立方程:,解得,
甲乙在12分钟时相遇;
(4)解:设此时起跑了分钟,
根据题意得,或或或,
解得:或或或,
5分钟或11分钟或13分钟或19分钟时甲乙相距250米.
【点睛】本题主要考查了一次函数的应用,求得甲乙两人的路程与时间的函数关系式是解题的关键.
23.(1)见解析
(2)①;②;③2
【分析】(1)设正方形的边长为,先根据折叠的性质证四边形是矩形,再根据是等腰直角三角形得出和的比例关系,即可得证结论;
(2)①作,,垂足分别为,,证,根据线段比例关系得出即可得出结论;
②作点关于直线的对称点,连接交于点,连接,此时周长最小,根据平行线分线段成比例求出此时线段的比值即可;
③根据题意得出点在以为直径的圆上,根据勾股定理求出的最小值即可.
【详解】(1)证明:设正方形的边长为,
是正方形的对角线,
,
由折叠的性质可知,
,
四边形的矩形,
是等腰直角三角形,
,
,
四边形是矩形;
(2)解:①如图,作,,垂足分别为,,
四边形是矩形,,
四边形是矩形,
,,,
,,
为的中点,
,,
,
,
,
,
;
②作点关于直线的对称点,连接交于点,连接,
此时最小等于,
则此时的周长最小,
,
,
设,则,
,
;
即
③四边形是矩形,,
,
,
点在以为直径的圆上,即的中点为,
,
最小,
故答案为:2.
【点睛】本题主要考查四边形的综合知识,解题的关键是熟练掌握矩形的性质,明确矩形的定义及掌握平行线分线段成比例、相似三角形的判定和性质等知识.
24.(1);;
(2)不存在满足条件的点
(3)
(4),
【分析】(1)设函数的表达式为:,即可求解;
(2)利用,即可求解;
(3),则,即可求解;
(4),,则,故,即可求解.
【详解】(1)解:设函数的表达式为:,
即:,
解得:.
故抛物线的表达式为:.
顶点坐标为;
故答案是:;;
(2)不存在,理由:
如答图1,连接,过点作轴的平行线交于点,
由题意得:,
∴直线的表达式为:,
设点,点,
则,
整理得:,
解得:,故方程无解,
则不存在满足条件的点;
(3)∵,
,
过作于,
,
,
∴
∴
∴点;
(4)如答图2,设直线交轴于点,
,,
,
,
则直线的表达式为:,
联立方程,得
解得:(舍去正值),
故点,.
【点睛】本题考查的是二次函数综合运用,涉及到一次函数、一元二次方程应用、图形的面积计算,掌握函数图像上点的坐标特征,待定系数法是关键.
同课章节目录
