2024年中考数学总复习验收卷(十)(含答案)
文档属性
| 名称 | 2024年中考数学总复习验收卷(十)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 21:31:36 | ||
图片预览




文档简介
2024年中考数学总复习验收卷(十)
数 学
(考试时间:120分钟 试卷满分:120 分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.(本题3分)实数的倒数的绝对值是( )
A. B. C.2023 D.
2.(本题3分)下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
3.(本题3分)下列运算正确的是( )
A. B. C. D.
4.(本题3分)为了落实“双减”政策,提倡课内高效学习,课外时间归还学生.“鸿志”班为了激发学生学习热情,提高学习成绩,采用分组学习方案,每6人分为一组,经过半个学期的学习,在定时作业测试中,某小组6人的数学成绩(单位:分)分别为130,135,125,140,130,120,关于这个小组数学成绩的统计分析,下列说法错误的是( )
A.平均数是130 B.中位数是130 C.众数是130 D.方差是40
5.(本题3分)由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最少有( )
A.7个 B.6个 C.5个 D.4个
6.(本题3分)如图,在三个空格中随机填上0,2,3三个数字,每个空格填一个数字,按从左往右的顺序恰好是“2023”的概率为 ( )
A. B. C. D.
7.(本题3分)将一把直尺与一块直角三角板按如图所示的方式放置,若,则的度数为( )
A. B. C. D.
8.(本题3分)如图,在等腰中,,,点M、N同时从点B出发,点M以的速度沿的方向运动到点C停止,点N以的速度沿的方向运动到点C停止,若的面积为(),运动时间为x(),那么y与x之间的函数图象大致是( )
B. C. D.
9.(本题3分)某校学生会以“心连心向未来”为主题,举办了庆祝香地回归25周年征文活动,选派20名学生会成员对120篇征文进行分类 ,现将20名学生会成员分为三组,若第一、二、三小组每人分别负责8 、6、5篇征文,且每组至少有2人,则学生会成员分组方案有( )
A.4种 B.5种 C.8种 D.9种
10.(本题3分)如图是抛物线的部分图象,其顶点坐标为,且与轴的一个交点在点和之间,则下列结论:①;②;③;④当时,;⑤一元二次方程有两个不相等的实数根,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(非选择题 共90分)
填空题(本大题共7个小题,每小题3分,共21分,直接填写答案.)
11.(本题3分)化学元素钉()是除铁()、钻()和镍()以外,在室温下具有独特磁性的第四个元素.钉()的原子半径约.将用科学记数法表示为______.
12.(本题3分)如图,已知平分.请添加一个条件:______,使.
13.(本题3分)圆锥的母线长为,其侧面展开图的圆心角为,则圆锥的底面圆半径长是______.
14.(本题3分)若关于x的分式方程无解,则k的值是_______.
15.(本题3分)如图,已知在平面直角坐标系中,等腰直角三角形的斜边轴于点A,经过点B的反比例函数的图象交边于点,连接,.若点是中点,的面积为1,则的值是______.
16.(本题3分)如图,在矩形中,,,M是边上的中点,N是边上的一动点,连接、将沿折叠,点B的对应点为点E,连接,当为直角三角形时,的长为_______.
17.(本题3分)如图,在平面直角坐标系中,四边形是正方形,点的坐标为,是以点为圆心,为半径的圆弧;是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,继续以点,,,为圆心按上述作法得到的曲线称为正方形的“渐开线”,则点的坐标是_______.
解答题(本大题共个7小题,共69分.解答应写出文字说明、证明过程或演算步骤.)
18.(本题10分)(本题共2个小题,第(1)题6分,第(2)题4分)
(1)计算;
(2).
19.(本题5分)解方程:;
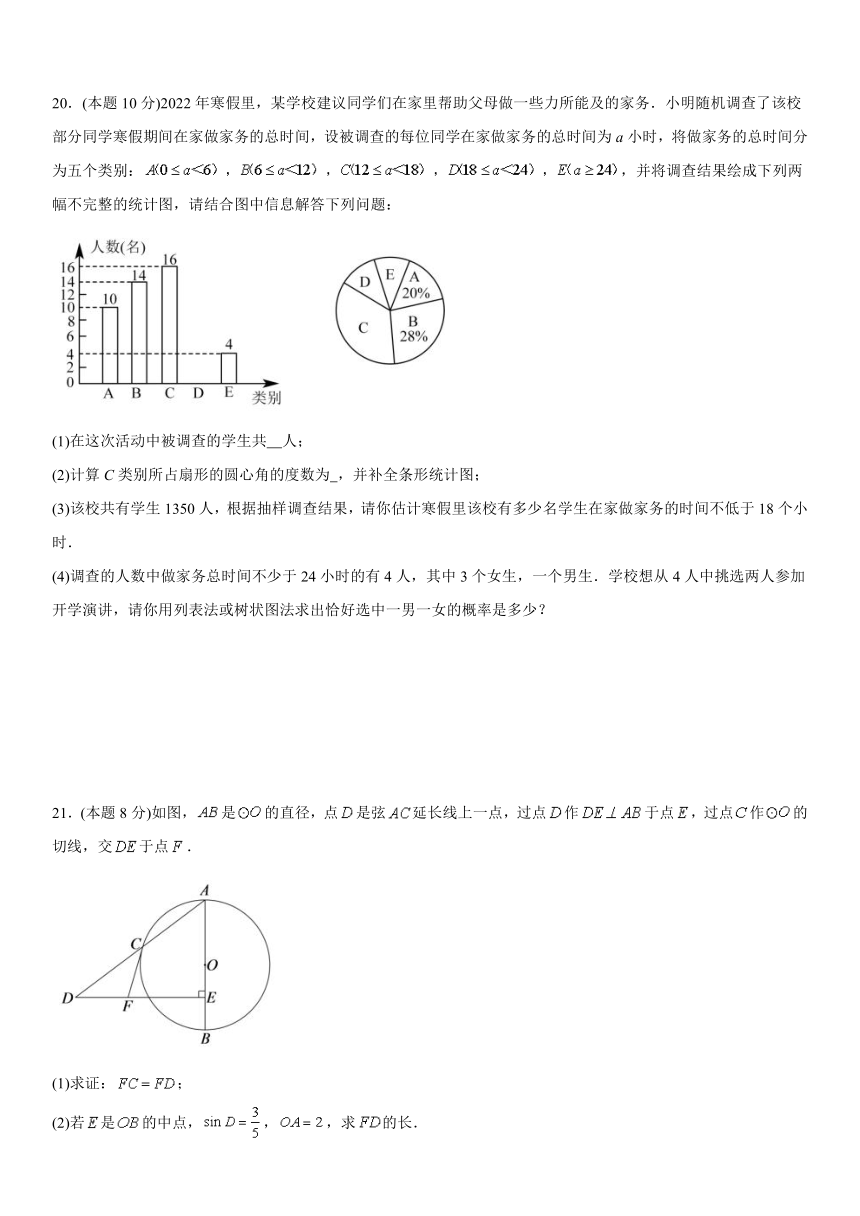
20.(本题10分)2022年寒假里,某学校建议同学们在家里帮助父母做一些力所能及的家务.小明随机调查了该校部分同学寒假期间在家做家务的总时间,设被调查的每位同学在家做家务的总时间为a小时,将做家务的总时间分为五个类别:,并将调查结果绘成下列两幅不完整的统计图,请结合图中信息解答下列问题:
(1)在这次活动中被调查的学生共 人;
(2)计算C类别所占扇形的圆心角的度数为 ,并补全条形统计图;
(3)该校共有学生1350人,根据抽样调查结果,请你估计寒假里该校有多少名学生在家做家务的时间不低于18个小时.
(4)调查的人数中做家务总时间不少于24小时的有4人,其中3个女生,一个男生.学校想从4人中挑选两人参加开学演讲,请你用列表法或树状图法求出恰好选中一男一女的概率是多少?
21.(本题8分)如图,是的直径,点是弦延长线上一点,过点作于点,过点作的切线,交于点.
(1)求证:;
(2)若是的中点,,,求的长.
22.(本题10分)甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
请结合图象信息解答下列问题:
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x的函数关系式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时与甲车相距15千米?直接写出答案.
23.(本题12分)如图1,在等腰三角形中,,连接.点M、N、P分别为的中点.
(1)当时,
①观察猜想:图1中,点D、E分别在边上,线段的数量关系是 ,的大小为 .
②探究证明:把绕点A顺时针方向旋转到如图2所示的位置,连接,求证:.
③在②的条件下,如图2,求证:是等边三角形
(2)拓展延伸:当时,,时,把绕点A在平面内自由旋转,如图3,请直接写出面积的最大值.
24.(本题14分)如图,已知直线与x轴,y轴交于B,A两点,抛物线经过点A,B.
(1)求抛物线的表达式;
(2)点P为线段上一个动点,过点P作垂直于x轴的直线交抛物线于点N,交直线于点M.设点P的横坐标为t.
①时,求点N的坐标.
②点C是直线上方抛物线上一点,当时,直接写出t的值.
③若点Q在平面内,当以Q,A,M,N为顶点的四边形是菱形时,直接写出点Q的纵坐标.
2024年中考数学总复习验收卷(十)
数学·参考答案
第Ⅰ卷
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10
A B C D B A A C B D
第Ⅱ卷
二、填空题(本大题共7小题,每小题3分,共21分)
11.;
12.(答案不唯一)
13.5
14.或
15.
16.7或
17.
三、解答题(本大题共7小题,满分69分)
18.(1)解:原式 ----------------------------4分
----------------------------1分
;----------------------------1分
(2)解:原式----------------------------2分
.----------------------------2分
19.解:
∵,----------------------------1分
∴,----------------------------1分
∴,----------------------------2分
∴,;----------------------------1分
20.(1)在这次活动中被调查的学生共(人),
故答案为:50;----------------------------1分
(2)C类别所占扇形的圆心角的度数为,----------------------------1分
D类别人数为(名),
补全图形如下:
----------------------------2分
故答案为:;
(3)估计该校在三月份在家做家务的时间不低于18个小时的学生有(名).----------------------------2分
(4)由上图可知,
----------------------------2分
一共有12种等可能结果,其中一男一女的情况有6种,
所以P(恰好选中一男一女)----------------------------2分
21.(1)证明:连接,如图1.----------------------------1分
∵是⊙的切线,是⊙的半径,
∴,
∴,----------------------------2分
∵,
∴,----------------------------3分
∵,
∴.
∴,----------------------------4分
∴;----------------------------5分
(2)解:连接,如图2.
∵,是的中点,
∴,,
在中,,
∴,
∴,----------------------------2分
设,则,
在中,.
在中,.
∴,解得.即的长为.----------------------------5分
22.解:(1)a=4.5,----------------------------1分
甲车的速度==60(千米/小时);----------------------------1分
(2)设乙开始的速度为v千米/小时,
则4v+(7﹣4.5)(v﹣50)=460,解得v=90(千米/小时),
4v=360,
则D(4,360),E(4.5,360),----------------------------1分
设直线EF的解析式为y=kx+b,
把E(4.5,360),F(7,460)代入得,
解得.----------------------------2分
所以线段EF所表示的y与x的函数关系式为y=40x+180(4.5≤x≤7);----------------------------2分(自变量取值范围占1分)
(3)甲车前40分钟的路程为60×=40千米,则C(0,40),
设直线CF的解析式为y=mx+n,
把C(0,40),F(7,460)代入得,解得,
所以直线CF的解析式为y=60x+40,
易得直线OD的解析式为y=90x(0≤x≤4),
设甲乙两车中途相遇点为G,由60x+40=90x,解得x=小时,即乙车出发小时后,甲乙两车相遇,
当乙车在OG段时,由60x+40﹣90x=15,解得x=,介于0~小时之间,符合题意;
当乙车在GD段时,由90x﹣(60x+40)=15,解得x=,介于~4小时之间,符合题意;
当乙车在DE段时,由360﹣(60x+40)=15,解得x=,不介于4~4.5之间,不符合题意;
当乙车在EF段时,由40x+180﹣(60x+40)=15,解得x=,介于4.5~7之间,符合题意.
所以乙车出发小时或小时或小时,乙与甲车相距15千米.----------------------------3分(直接写出答案每个1分,写错不扣分,多写扣1分)
23.【详解】(1)①解:∵,
∴,
∵点M、N、P分别为的中点,
∴是的中位线,是的中位线,,
∴,,,,
∴,
∴,
∵,
∴,
故答案为:----------------------------2分,;----------------------------2分
②证明:由旋转的性质得:,
∵,
∴,
∴,----------------------------2分
③证明:∵点M、N、P分别为的中点,
∴是的中位线,是的中位线,,
∴,,,,
∴,
∴,
∵,
∴,
∴是等边三角形;----------------------------4分
(2)由题意得:,即,
同(1)得:,
∴是等腰直角三角形,
∴,
∴当时,最大,此时,如图4所示:
,
∴面积的最大值为32.----------------------------2分
24.(1)解:当时,,
∴点A的坐标为;
当时,,
解得:,
∴点B的坐标为.----------------------------1分
将A,B代入,得:,
解得:,----------------------------2分
∴这个抛物线的解析式为;----------------------------3分
(2)解:①设点P的坐标为,则点N的坐标为,点M的坐标为,----------------------------1分
∴,,----------------------------2分
∵,
∴,----------------------------3分
解得或(舍),
∴N;----------------------------4分
②当时,如图1.
设点P的坐标为,则点N的坐标为,点C的坐标为,点M的坐标为,
∴,,
∵,
∴,即,
解得:,(舍去),,(舍去),
∴或,
∴当时,点C的坐标为或;----------------------------4分(写出一个得2分)
③∵A,N,M,
∴,
,
,
若以Q、A、M、N为顶点的四边形是菱形,则为等腰三角形,需要分以下三种情况:
当时,,
解得(舍)或(舍)或,
∴A,N,M,
由菱形的性质可知,点Q的坐标为;
当时,,
解得(舍)或(舍)或,
此时,
由菱形的性质可知,Q,即Q;
当时,,
解得(舍)或,
此时,
由菱形的性质可知,Q,即Q;
综上,点Q的纵坐标为:2或或.----------------------------3分(写出一个得1分)
数 学
(考试时间:120分钟 试卷满分:120 分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.(本题3分)实数的倒数的绝对值是( )
A. B. C.2023 D.
2.(本题3分)下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
3.(本题3分)下列运算正确的是( )
A. B. C. D.
4.(本题3分)为了落实“双减”政策,提倡课内高效学习,课外时间归还学生.“鸿志”班为了激发学生学习热情,提高学习成绩,采用分组学习方案,每6人分为一组,经过半个学期的学习,在定时作业测试中,某小组6人的数学成绩(单位:分)分别为130,135,125,140,130,120,关于这个小组数学成绩的统计分析,下列说法错误的是( )
A.平均数是130 B.中位数是130 C.众数是130 D.方差是40
5.(本题3分)由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最少有( )
A.7个 B.6个 C.5个 D.4个
6.(本题3分)如图,在三个空格中随机填上0,2,3三个数字,每个空格填一个数字,按从左往右的顺序恰好是“2023”的概率为 ( )
A. B. C. D.
7.(本题3分)将一把直尺与一块直角三角板按如图所示的方式放置,若,则的度数为( )
A. B. C. D.
8.(本题3分)如图,在等腰中,,,点M、N同时从点B出发,点M以的速度沿的方向运动到点C停止,点N以的速度沿的方向运动到点C停止,若的面积为(),运动时间为x(),那么y与x之间的函数图象大致是( )
B. C. D.
9.(本题3分)某校学生会以“心连心向未来”为主题,举办了庆祝香地回归25周年征文活动,选派20名学生会成员对120篇征文进行分类 ,现将20名学生会成员分为三组,若第一、二、三小组每人分别负责8 、6、5篇征文,且每组至少有2人,则学生会成员分组方案有( )
A.4种 B.5种 C.8种 D.9种
10.(本题3分)如图是抛物线的部分图象,其顶点坐标为,且与轴的一个交点在点和之间,则下列结论:①;②;③;④当时,;⑤一元二次方程有两个不相等的实数根,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(非选择题 共90分)
填空题(本大题共7个小题,每小题3分,共21分,直接填写答案.)
11.(本题3分)化学元素钉()是除铁()、钻()和镍()以外,在室温下具有独特磁性的第四个元素.钉()的原子半径约.将用科学记数法表示为______.
12.(本题3分)如图,已知平分.请添加一个条件:______,使.
13.(本题3分)圆锥的母线长为,其侧面展开图的圆心角为,则圆锥的底面圆半径长是______.
14.(本题3分)若关于x的分式方程无解,则k的值是_______.
15.(本题3分)如图,已知在平面直角坐标系中,等腰直角三角形的斜边轴于点A,经过点B的反比例函数的图象交边于点,连接,.若点是中点,的面积为1,则的值是______.
16.(本题3分)如图,在矩形中,,,M是边上的中点,N是边上的一动点,连接、将沿折叠,点B的对应点为点E,连接,当为直角三角形时,的长为_______.
17.(本题3分)如图,在平面直角坐标系中,四边形是正方形,点的坐标为,是以点为圆心,为半径的圆弧;是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,继续以点,,,为圆心按上述作法得到的曲线称为正方形的“渐开线”,则点的坐标是_______.
解答题(本大题共个7小题,共69分.解答应写出文字说明、证明过程或演算步骤.)
18.(本题10分)(本题共2个小题,第(1)题6分,第(2)题4分)
(1)计算;
(2).
19.(本题5分)解方程:;
20.(本题10分)2022年寒假里,某学校建议同学们在家里帮助父母做一些力所能及的家务.小明随机调查了该校部分同学寒假期间在家做家务的总时间,设被调查的每位同学在家做家务的总时间为a小时,将做家务的总时间分为五个类别:,并将调查结果绘成下列两幅不完整的统计图,请结合图中信息解答下列问题:
(1)在这次活动中被调查的学生共 人;
(2)计算C类别所占扇形的圆心角的度数为 ,并补全条形统计图;
(3)该校共有学生1350人,根据抽样调查结果,请你估计寒假里该校有多少名学生在家做家务的时间不低于18个小时.
(4)调查的人数中做家务总时间不少于24小时的有4人,其中3个女生,一个男生.学校想从4人中挑选两人参加开学演讲,请你用列表法或树状图法求出恰好选中一男一女的概率是多少?
21.(本题8分)如图,是的直径,点是弦延长线上一点,过点作于点,过点作的切线,交于点.
(1)求证:;
(2)若是的中点,,,求的长.
22.(本题10分)甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
请结合图象信息解答下列问题:
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x的函数关系式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时与甲车相距15千米?直接写出答案.
23.(本题12分)如图1,在等腰三角形中,,连接.点M、N、P分别为的中点.
(1)当时,
①观察猜想:图1中,点D、E分别在边上,线段的数量关系是 ,的大小为 .
②探究证明:把绕点A顺时针方向旋转到如图2所示的位置,连接,求证:.
③在②的条件下,如图2,求证:是等边三角形
(2)拓展延伸:当时,,时,把绕点A在平面内自由旋转,如图3,请直接写出面积的最大值.
24.(本题14分)如图,已知直线与x轴,y轴交于B,A两点,抛物线经过点A,B.
(1)求抛物线的表达式;
(2)点P为线段上一个动点,过点P作垂直于x轴的直线交抛物线于点N,交直线于点M.设点P的横坐标为t.
①时,求点N的坐标.
②点C是直线上方抛物线上一点,当时,直接写出t的值.
③若点Q在平面内,当以Q,A,M,N为顶点的四边形是菱形时,直接写出点Q的纵坐标.
2024年中考数学总复习验收卷(十)
数学·参考答案
第Ⅰ卷
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10
A B C D B A A C B D
第Ⅱ卷
二、填空题(本大题共7小题,每小题3分,共21分)
11.;
12.(答案不唯一)
13.5
14.或
15.
16.7或
17.
三、解答题(本大题共7小题,满分69分)
18.(1)解:原式 ----------------------------4分
----------------------------1分
;----------------------------1分
(2)解:原式----------------------------2分
.----------------------------2分
19.解:
∵,----------------------------1分
∴,----------------------------1分
∴,----------------------------2分
∴,;----------------------------1分
20.(1)在这次活动中被调查的学生共(人),
故答案为:50;----------------------------1分
(2)C类别所占扇形的圆心角的度数为,----------------------------1分
D类别人数为(名),
补全图形如下:
----------------------------2分
故答案为:;
(3)估计该校在三月份在家做家务的时间不低于18个小时的学生有(名).----------------------------2分
(4)由上图可知,
----------------------------2分
一共有12种等可能结果,其中一男一女的情况有6种,
所以P(恰好选中一男一女)----------------------------2分
21.(1)证明:连接,如图1.----------------------------1分
∵是⊙的切线,是⊙的半径,
∴,
∴,----------------------------2分
∵,
∴,----------------------------3分
∵,
∴.
∴,----------------------------4分
∴;----------------------------5分
(2)解:连接,如图2.
∵,是的中点,
∴,,
在中,,
∴,
∴,----------------------------2分
设,则,
在中,.
在中,.
∴,解得.即的长为.----------------------------5分
22.解:(1)a=4.5,----------------------------1分
甲车的速度==60(千米/小时);----------------------------1分
(2)设乙开始的速度为v千米/小时,
则4v+(7﹣4.5)(v﹣50)=460,解得v=90(千米/小时),
4v=360,
则D(4,360),E(4.5,360),----------------------------1分
设直线EF的解析式为y=kx+b,
把E(4.5,360),F(7,460)代入得,
解得.----------------------------2分
所以线段EF所表示的y与x的函数关系式为y=40x+180(4.5≤x≤7);----------------------------2分(自变量取值范围占1分)
(3)甲车前40分钟的路程为60×=40千米,则C(0,40),
设直线CF的解析式为y=mx+n,
把C(0,40),F(7,460)代入得,解得,
所以直线CF的解析式为y=60x+40,
易得直线OD的解析式为y=90x(0≤x≤4),
设甲乙两车中途相遇点为G,由60x+40=90x,解得x=小时,即乙车出发小时后,甲乙两车相遇,
当乙车在OG段时,由60x+40﹣90x=15,解得x=,介于0~小时之间,符合题意;
当乙车在GD段时,由90x﹣(60x+40)=15,解得x=,介于~4小时之间,符合题意;
当乙车在DE段时,由360﹣(60x+40)=15,解得x=,不介于4~4.5之间,不符合题意;
当乙车在EF段时,由40x+180﹣(60x+40)=15,解得x=,介于4.5~7之间,符合题意.
所以乙车出发小时或小时或小时,乙与甲车相距15千米.----------------------------3分(直接写出答案每个1分,写错不扣分,多写扣1分)
23.【详解】(1)①解:∵,
∴,
∵点M、N、P分别为的中点,
∴是的中位线,是的中位线,,
∴,,,,
∴,
∴,
∵,
∴,
故答案为:----------------------------2分,;----------------------------2分
②证明:由旋转的性质得:,
∵,
∴,
∴,----------------------------2分
③证明:∵点M、N、P分别为的中点,
∴是的中位线,是的中位线,,
∴,,,,
∴,
∴,
∵,
∴,
∴是等边三角形;----------------------------4分
(2)由题意得:,即,
同(1)得:,
∴是等腰直角三角形,
∴,
∴当时,最大,此时,如图4所示:
,
∴面积的最大值为32.----------------------------2分
24.(1)解:当时,,
∴点A的坐标为;
当时,,
解得:,
∴点B的坐标为.----------------------------1分
将A,B代入,得:,
解得:,----------------------------2分
∴这个抛物线的解析式为;----------------------------3分
(2)解:①设点P的坐标为,则点N的坐标为,点M的坐标为,----------------------------1分
∴,,----------------------------2分
∵,
∴,----------------------------3分
解得或(舍),
∴N;----------------------------4分
②当时,如图1.
设点P的坐标为,则点N的坐标为,点C的坐标为,点M的坐标为,
∴,,
∵,
∴,即,
解得:,(舍去),,(舍去),
∴或,
∴当时,点C的坐标为或;----------------------------4分(写出一个得2分)
③∵A,N,M,
∴,
,
,
若以Q、A、M、N为顶点的四边形是菱形,则为等腰三角形,需要分以下三种情况:
当时,,
解得(舍)或(舍)或,
∴A,N,M,
由菱形的性质可知,点Q的坐标为;
当时,,
解得(舍)或(舍)或,
此时,
由菱形的性质可知,Q,即Q;
当时,,
解得(舍)或,
此时,
由菱形的性质可知,Q,即Q;
综上,点Q的纵坐标为:2或或.----------------------------3分(写出一个得1分)
同课章节目录
