9.2用样本估计总体 同步练习(含解析)
文档属性
| 名称 | 9.2用样本估计总体 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:57:49 | ||
图片预览




文档简介
9.2用样本估计整体同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
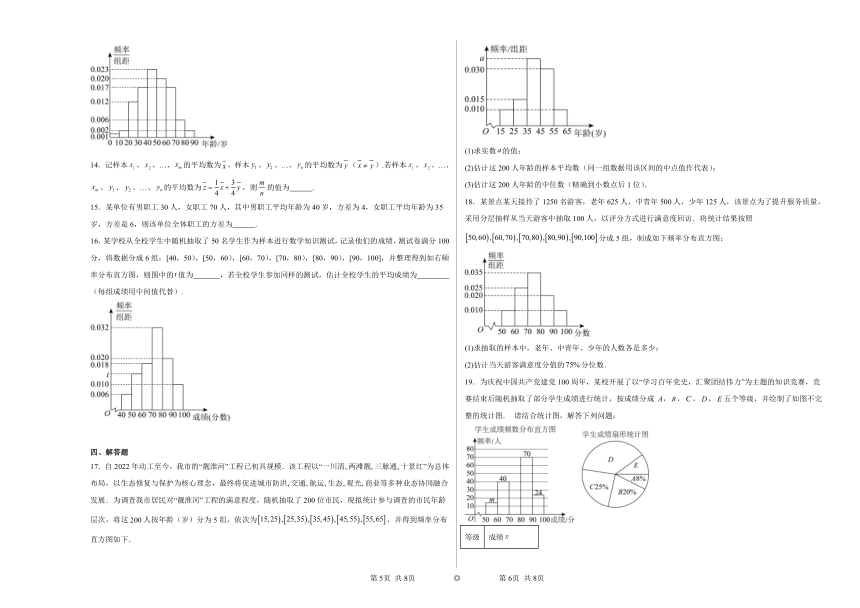
1.2023年是共建“一带一路”倡议提出十周年.而今“一带一路”已成为当今世界最受欢迎的国际公共产晶和最大规模的国际合作平台.树人中学历史学科组近期开展了“回望丝路”系列主题活动,组织“一带一路”知识竞赛,并对学生成绩进行了汇总整理,形成以下直方图.该校学生“一带一路”知识竞赛成绩的第60百分位数大约为( )
A.72 B.76 C.78 D.85
2.已知数据,,…,的平均数和方差分别为4,10,那么数据,,…,的平均数和方差分别为( )
A., B.1, C., D.,
3.从某公司生产的产品中任意抽取12件,得到它们的质量(单位:)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0,则这组数据的四分位数不可能是( )
A.8.75 B.8.15 C.9.9 D.8.5
4.在高一新生入学时,某班体育委员统计了本班所有同学中考体育成绩的平均分和方差.后来又转来一位新同学,若该同学中考体育成绩恰好是这个班级之前中考体育成绩的平均分,则在这位同学转来之后,该班级的中考体育成绩的( )
A.平均分不变,方差变小 B.平均分不变,方差变大
C.平均分变大,方差变小 D.平均分变小,方差变大
5.如图为2021~2022年中国十大行业人工智能应用渗透率,则下列说法错误的是( )
A.2021年与2022年人工智能应用渗透率最低的行业都是教育
B.与2021年相比,2022年人工智能应用渗透率增长最快的是金融行业
C.2021年十大行业人工智能应用渗透率的极差为56%
D.2022年十大行业人工智能应用渗透率的中位数是42.5%
6.为了鼓励学生积极锻炼身体,强健体魄,某学校决定每学期对体育成绩在年级前100名的学生给予专项奖励.已知该校高三年级共有600名学生,如图是该年级学生本学期体育测试成绩的频率分布直方图.据此估计,该校高三年级学生体育成绩的中位数为( )
A.70 B.70.5 C.71.25 D.72
7.恩格尔系数是由德国统计学家恩斯特 恩格尔提出的,计算公式是“恩格尔系数”.恩格尔系数是国际上通用的衡量居民生活水平高低的一项重要指标,一般随居民家庭收入和生活水平的提高而下降,恩格尔系数达60%以上为贫困,为温饱,为小康,为富裕,低于为最富裕.如图是近十年我国农村与城镇居民的恩格尔系数折线图,由图可知下列结论正确的是( )
A.城镇居民从2013年开始进入“最富裕”水平
B.农村居民恩格尔系数的平均数低于
C.城镇居民恩格尔系数的第45百分位数高于
D.全国居民恩格尔系数等于农村居民恩格尔系数和城镇居民恩格尔系数的平均数
8.因学校政治老师比较紧缺,高一年级为了了解学生选科中包含“政治”这一科目的学生人数便于安排教学.从高一年级中随机抽取了五个班,把每个班选科中包含“政治”的人数作为样本数据.已知样本平均数为7,样本方差为4,且样本数据各不相同,则样本数据中的最大值为( )
A.8 B.9 C.10 D.11
二、多选题
9.某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为的样本,其频率分布直方图如图,其中支出在元的学生有人,则下列说法正确的是( )
A.样本中支出在元的频率为
B.采用分层抽样从人中抽出人,则在中共需抽出人
C.的值为
D.该校学生一周生活方面支出的中位数大约是元(精确到个位数)
10.党的二十大作出“发展海洋经济,保护海洋生态环境,加快建设海洋强国”的战略部署.如图是2018—2023年中国海洋生产总值的条形统计图,根据图中数据可知下列结论正确的是( )
A.从2018年开始,中国海洋生产总值逐年增大
B.从2019年开始,中国海洋生产总值的年增长率最大的是2021年
C.这6年中国海洋生产总值的极差为15122
D.这6年中国海洋生产总值的80%分位数是94628
11.已知样本甲:与样本乙:满足关系,则下列结论错误的是( )
A.样本乙的极差等于样本甲的极差
B.若某个为样本甲的中位数,则是样本乙的中位数
C.样本乙的众数小于样本甲的众数
D.若某个为样本甲的平均数,则是样本乙的平均数
12.2023年8月8日是我国第15个“全民健身日”,“全民健身日”提升全民健身意识,让健身成为一种习惯和风俗,为倡导健康生活方式,某大学社团联合学生会倡议全校学生参与“每日万步行”健走活动.下图为该校甲、乙两名同学在同一星期内每日步数的折线统计图,则下列说法正确的是( )
A.这一星期内甲的日步数的中位数小于乙的日步数的中位数
B.这一星期内甲的日步数的平均数大于乙的日步数的平均数
C.这一星期内乙的日步数的标准差小于甲的日步数的标准差
D.这一星期内乙的日步数的分位数是12400
三、填空题
13.在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到如图的样本数据的频率分布直方图,则这种疾病患者的平均年龄为 .
14.记样本、、…、的平均数为,样本、、…、的平均数为().若样本、、…、、、、…、的平均数为,则的值为 .
15.某单位有男职工30人,女职工70人,其中男职工平均年龄为40岁,方差为4,女职工平均年龄为35岁,方差是6,则该单位全体职工的方差为 .
16.某学校从全校学生中随机抽取了50名学生作为样本进行数学知识测试,记录他们的成绩,测试卷满分100分,将数据分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并整理得到如右频率分布直方图,则图中的值为 ,若全校学生参加同样的测试,估计全校学生的平均成绩为 (每组成绩用中间值代替).
四、解答题
17.自2022年动工至今,我市的“靓淮河”工程已初具规模.该工程以“一川清 两滩靓 三脉通 十景红”为总体布局,以生态修复与保护为核心理念,最终将促进城市防洪 交通 航运 生态 观光 商业等多种业态协同融合发展.为调查我市居民对“靓淮河”工程的满意程度,随机抽取了200位市民,现拟统计参与调查的市民年龄层次,将这200人按年龄(岁)分为5组,依次为,并得到频率分布直方图如下.
(1)求实数的值;
(2)估计这200人年龄的样本平均数(同一组数据用该区间的中点值作代表);
(3)估计这200人年龄的中位数(精确到小数点后1位).
18.某景点某天接待了1250名游客,老年625人,中青年500人,少年125人,该景点为了提升服务质量,采用分层抽样从当天游客中抽取100人,以评分方式进行满意度回访.将统计结果按照分成5组,制成如下频率分布直方图:
(1)求抽取的样本中,老年、中青年、少年的人数各是多少;
(2)估计当天游客满意度分值的分位数.
19.为庆祝中国共产党建党100周年,某校开展了以“学习百年党史,汇聚团结伟力”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成 A,,,,五个等级,并绘制了如图不完整的统计图. 请结合统计图,解答下列问题:
等级 成绩
(1)本次调查一共随机抽取了 名学生的成绩,频数分布直方图中 ;
(2)补全学生成绩频数分布直方图;
(3)若成绩在80分及以上为优秀,全校共有2000名学生,估计成绩优秀的学生有多少人?
20.某日数学老师进行了一次小测验,两班一共有100名学生参加了测验,成绩都在内,按照,,…,分组,得到如下频率分布直方图:
(1)求两班全体学生成绩的平均数;(每组数据以区间中点值为代表)
(2)若根据测试成绩从高到低进行排顺序,预定前40名为达标人数,估计应该把达标分数线约定为多少分.
21.文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者.某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:得到如图所示的频率分布直方图.
(1)求频率分布直方图中的值和样本成绩的四分位数;
(2)已知落在的平均成绩是65,方差是11,落在的平均成绩为75,方差是16,求两组成绩的总平均数和总方差.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据频率分布直方图直接计算即可.
【详解】由题中频率分布直方图知区间的频率为:
则在区间的频率为:,
所以第60百分位数在区间,且设为,则,
解得.
故选:B
2.D
【分析】利用平均数与方差的运算性质求解即可.
【详解】设数据,,…,的平均数和方差分别为和,
则数据,,…,的平均数为,方差为,
得,,
故选:D.
3.C
【分析】将这组数据从小到大排序,根据百分位数的概念,即可得到答案.
【详解】将这12个数据从小到大排序得:7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9,
由,可知这组数据的第25百分位数为,
由,可知这组数据的第50百分位数为,
由,可知这组数据的第75百分位数为,所以这组数据的四分位数不可能是9.9.
故选:C
4.A
【分析】根据平均数和方差的计算公式判断即可.
【详解】设该班原有位同学,中考体育成绩的平均分为,方差为,
则,,
故,,
则转来一位新同学后该班中考体育成绩的平均分为,
方差为,
故该班中考体育成绩的平均分不变,方差变小.
故选:A.
5.B
【分析】根据统计图中的数据判断即可.
【详解】由图易得A正确;
对于选项B:互联网的增长率为:;金融的增长率为:;
政府的增长率为:;电信的增长率为:;
显然金融的增长率小于电信的增长率;增长最快的不是金融行业,故B错误;
对于选项C:2021年十大行业人工智能应用渗透率的极差为,故C正确;
对于选项D:2022年十大行业人工智能应用渗透率的中位数是,故D正确.
故选:B.
6.C
【分析】根据题意,结合频率分布直方图的中位数的计算方法,即可求解.
【详解】由给定的频率分布直方图,可得前2个矩形的面积为,
前3个小矩形的面积为,
所以学生体育成绩的中位数位于之间,
设学生体育成绩的总位数为,可得分.
故选:C.
7.C
【分析】对于A,直接观察折线统计图即可判断;对于B,结合平均数的定义以及图中数据判断即可;对于C,结合百分位数的定义即可判断;对于D,无法确定农村居民与城镇居民的比例,由此即可判断.
【详解】对于A:从折线统计图可知2015年开始城镇居民的恩格尔系数均低于,
即从2015年开始进入“最富裕”水平,故A错误;
对于B:农村居民恩格尔系数只有2017 2018 2019这三年在30%到32%之间,
其余年份均大于,且2012 2013这两年大于(等于),
故农村居民恩格尔系数的平均数高于,故B错误;
对于C:城镇居民恩格尔系数从小到大排列(所对应的年份)前5位分别为2019 2018 2017 2021 2020,因为,
所以第45百分位数为第5位,即2020年的恩格尔系数,由图可知2020年的恩格尔系数高于,故C正确;
对于D:由于无法确定农村居民与城镇居民的比例,
故不能用农村居民恩格尔系数和城镇居民恩格尔系数的平均数作为全国居民恩格尔系数,故D错误.
故选:C.
8.C
【分析】分析题意,利用均值和方差的定义列方程求解即可.
【详解】设五个班级参加的人数分别为,由题意得,,分析得必定为,故,解得,或,,解得或,显然人数从低到高为,故最大值为.
故选:C
9.BCD
【分析】利用频率分布直方图中所有矩形的面积之和为,可判断A选项;计算出样本中支出在的频率,结合分层抽样可判断B选项;利用频率、频数以及样本总容量的关系可判断C选项;利用频率分布直方图计算出中位数,可判断D选项.
【详解】对于A选项,样本中支出在元的频率为,A错;
对于B选项,样本中支出在的频率为,
所以,采用分层抽样从人中抽出人,则在中共需抽出的人数为,B对;
对于C选项,,C对;
对于D选项,前两个矩形的面积之和为,
前三个矩形的面积之和为,
设样本中支出的中位数为,则,且,解得,
所以,该校学生一周生活方面支出的中位数大约是元(精确到个位数),D对.
故选:BCD.
10.BD
【分析】对A,根据条形图数据可判断;对B,根据数据计算年增长率可判断;对C,计算极差可判断;对D,根据80%分位数概念计算可判断.
【详解】对于A,根据条形图数据可以看到2020年较2019年海洋生产总值是下降的,故A错误;
对于B,2019年海洋生产总值年增长率是,
2020年海洋生产总值年增长率是,2021年海洋生产总值年增长率是,
2022年海洋生产总值年增长率是,2023年海洋生产总值年增长率是,
故年增长率最大的是2021年,故B正确;
对于C,这6年中国海洋生产总值的极差为,故C错误;
对于D,将这6年的海洋生产总值按照从小到大排列80010,83415,89415,90385,94628,98537,又,
所以这6年中国海洋生产总值的80%分位数是94628,故D正确.
故选:BD.
11.ACD
【分析】利用极差、众数、中位数、平均数的定义和性质即可求解.
【详解】由样本甲:,,,…,与样本乙:,,,…,满足,知:
样本乙的极差不等于样本甲的极差,例如样本甲:0,1,2与样本乙:,故A中结论不正确;
不妨令,
因为在上单调递减,则,
所以若某个为样本甲的中位数,则是样本乙的中位数,故B中结论正确;
因为在上单调递减,则样本乙的众数等于样本甲的众数,故C中结论不正确;
若某个为样本甲的平均数,则不一定是样本乙的平均数,
例如样本甲:0,1,2与样本乙:,故D中结论不正确.
故选:ABD.
12.BC
【分析】根据折线图得到这一星期内甲,乙的日步数,都从小到大进行排列,得到中位数后即可判断选项A;根据平均数计算公式,计算出这一星期内甲,乙的日步数的平均数,比较大小即可判断选项B;根据图象观察甲的波动程度较大,故方差较大,从而判断选项C;把乙一星期内的步数从小到大进行排列,并计算,故第六个数为所求,即可判断选项D.
【详解】由折线图可得甲一星期内的步数从小到大的排列为:
,所以中位数为12600;
由折线图可得乙一星期内的步数从小到大的排列为:
,所以中位数为12600;
故这一星期内甲、乙的日步数的中位数都为12600,A错误;
这一星期内甲的日步数的平均数为:
,
这一星期内乙的日步数的平均数为:
,
因为,故B正确;
由图知,甲的波动程度较大,故方差,标准差较大,故C正确;
乙一星期内的步数从小到大的排列为:
,故这一星期内乙的日步数的分位数是13800,故D错误.
故选:BC.
13.
【分析】根据频率分布直方图中平均数的求法求值即可.
【详解】由题意知:平均年龄(岁).
故答案为:.
14.
【分析】根据平均数公式运算求解即可.
【详解】因为样本、、…、的平均数为,可得,
样本、、…、的平均数为,可得,
又因为样本、、…、、、、…、的平均数为
,
且,整理得,即.
故答案为:.
15.10.65
【分析】利用由部分方差求总体方差的公式求解.
【详解】由题意得,该单位全体职工的平均年龄为岁,
则该单位全体职工的方差
.
故答案为:10.65
16.
【分析】由频率分布直方图中总面积为可计算出,由频率分布直方图中平均数的计算方式计算平均数即可估计全校学生的平均成绩.
【详解】由频率分布直方图中总面积为,
即,
解得,
,
故可估计全校学生的平均成绩为.
故答案为:;.
17.(1)
(2)41.5岁
(3)42.1岁
【分析】(1)根据频率之和为1,可求的值;
(2)根据频率分布直方图,可直接估算平均数;
(3)直接求频率在的数据就可估计中位数.
【详解】(1)由题意:,解得.
(2)由题意:,
估计这200人年龄的样本平均数为41.5岁.
(3)由图可知,年龄在的频率为0.25,在的频率为0.35,
,
估计这200人年龄的样本中位数为42.1岁.
18.(1)50人,40人,10人
(2)82.5
【分析】(1)求出老年、中青年、少年的人数比例,从而求抽取样本中老年、中青年、少年的人数;
(2)利用百分位数的定义进行求解即可得.
【详解】(1)老年625人,中青年500人,少年125人,
故老年、中青年、少年的人数比例为,
故抽取100人,样本中老年人数为人,
中青年人数为人,少年人数为人;
(2)设当天游客满意度分值的分位数为,
因为,
,
所以位于区间内,
则,解得:,
所以估计当天游客满意度分值的分位数为.
19.(1)200;
(2)答案见解析;
(3)
【分析】(1)根据扇形图与频率分布直方图数据计算即可;
(2)根据表格补全频率分布直方图即可;
(3)由等级D、E占比估计整体即可.
【详解】(1)根据扇形图及频率分布直方图可知B等级有40人,占总人数的20%,
则有;
(2)由(1)知等级人,补图如下:
(3)由扇形图可知成绩在80分及以上的D、E等级占比为,
所以优秀的总人数估计有人.
20.(1)99
(2)109分
【分析】(1)由所有频率和为1,列方程求出的值,由平均数公式求解即可,
(2)设分数线定为,根据频率分布直方图可知,列出方程估计录取的分线.
【详解】(1)由题意得,解得,
两班全体学生成绩的平均数为
.
(2)根据题意,达标的比例为,
设分数线定为,根据频率分布直方图可知,
则,解得,
所以估计应该把达标分数线定为109分.
21.(1),65,75,84
(2)71,38
【分析】(1)由频率分布直方图的性质即可求解;
(2)由和组的平均数和方差即可求得总平均数和总方差.
【详解】(1)利用每组小矩形的面积之和为1可得,
,解得.
四分位数分别为第25百分位数,第50百分位数,第75百分位数,
设第百分位数为,则;
设第百分位数为,则;
设第百分位数为,则;
所以该数据的四分位数分别为65,75,84.
(2)由图可知,成绩在的市民人数为,
成绩在的市民人数为,
所以;
由样本方差计算总体方差公式可得总方差为
.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.2023年是共建“一带一路”倡议提出十周年.而今“一带一路”已成为当今世界最受欢迎的国际公共产晶和最大规模的国际合作平台.树人中学历史学科组近期开展了“回望丝路”系列主题活动,组织“一带一路”知识竞赛,并对学生成绩进行了汇总整理,形成以下直方图.该校学生“一带一路”知识竞赛成绩的第60百分位数大约为( )
A.72 B.76 C.78 D.85
2.已知数据,,…,的平均数和方差分别为4,10,那么数据,,…,的平均数和方差分别为( )
A., B.1, C., D.,
3.从某公司生产的产品中任意抽取12件,得到它们的质量(单位:)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0,则这组数据的四分位数不可能是( )
A.8.75 B.8.15 C.9.9 D.8.5
4.在高一新生入学时,某班体育委员统计了本班所有同学中考体育成绩的平均分和方差.后来又转来一位新同学,若该同学中考体育成绩恰好是这个班级之前中考体育成绩的平均分,则在这位同学转来之后,该班级的中考体育成绩的( )
A.平均分不变,方差变小 B.平均分不变,方差变大
C.平均分变大,方差变小 D.平均分变小,方差变大
5.如图为2021~2022年中国十大行业人工智能应用渗透率,则下列说法错误的是( )
A.2021年与2022年人工智能应用渗透率最低的行业都是教育
B.与2021年相比,2022年人工智能应用渗透率增长最快的是金融行业
C.2021年十大行业人工智能应用渗透率的极差为56%
D.2022年十大行业人工智能应用渗透率的中位数是42.5%
6.为了鼓励学生积极锻炼身体,强健体魄,某学校决定每学期对体育成绩在年级前100名的学生给予专项奖励.已知该校高三年级共有600名学生,如图是该年级学生本学期体育测试成绩的频率分布直方图.据此估计,该校高三年级学生体育成绩的中位数为( )
A.70 B.70.5 C.71.25 D.72
7.恩格尔系数是由德国统计学家恩斯特 恩格尔提出的,计算公式是“恩格尔系数”.恩格尔系数是国际上通用的衡量居民生活水平高低的一项重要指标,一般随居民家庭收入和生活水平的提高而下降,恩格尔系数达60%以上为贫困,为温饱,为小康,为富裕,低于为最富裕.如图是近十年我国农村与城镇居民的恩格尔系数折线图,由图可知下列结论正确的是( )
A.城镇居民从2013年开始进入“最富裕”水平
B.农村居民恩格尔系数的平均数低于
C.城镇居民恩格尔系数的第45百分位数高于
D.全国居民恩格尔系数等于农村居民恩格尔系数和城镇居民恩格尔系数的平均数
8.因学校政治老师比较紧缺,高一年级为了了解学生选科中包含“政治”这一科目的学生人数便于安排教学.从高一年级中随机抽取了五个班,把每个班选科中包含“政治”的人数作为样本数据.已知样本平均数为7,样本方差为4,且样本数据各不相同,则样本数据中的最大值为( )
A.8 B.9 C.10 D.11
二、多选题
9.某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为的样本,其频率分布直方图如图,其中支出在元的学生有人,则下列说法正确的是( )
A.样本中支出在元的频率为
B.采用分层抽样从人中抽出人,则在中共需抽出人
C.的值为
D.该校学生一周生活方面支出的中位数大约是元(精确到个位数)
10.党的二十大作出“发展海洋经济,保护海洋生态环境,加快建设海洋强国”的战略部署.如图是2018—2023年中国海洋生产总值的条形统计图,根据图中数据可知下列结论正确的是( )
A.从2018年开始,中国海洋生产总值逐年增大
B.从2019年开始,中国海洋生产总值的年增长率最大的是2021年
C.这6年中国海洋生产总值的极差为15122
D.这6年中国海洋生产总值的80%分位数是94628
11.已知样本甲:与样本乙:满足关系,则下列结论错误的是( )
A.样本乙的极差等于样本甲的极差
B.若某个为样本甲的中位数,则是样本乙的中位数
C.样本乙的众数小于样本甲的众数
D.若某个为样本甲的平均数,则是样本乙的平均数
12.2023年8月8日是我国第15个“全民健身日”,“全民健身日”提升全民健身意识,让健身成为一种习惯和风俗,为倡导健康生活方式,某大学社团联合学生会倡议全校学生参与“每日万步行”健走活动.下图为该校甲、乙两名同学在同一星期内每日步数的折线统计图,则下列说法正确的是( )
A.这一星期内甲的日步数的中位数小于乙的日步数的中位数
B.这一星期内甲的日步数的平均数大于乙的日步数的平均数
C.这一星期内乙的日步数的标准差小于甲的日步数的标准差
D.这一星期内乙的日步数的分位数是12400
三、填空题
13.在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到如图的样本数据的频率分布直方图,则这种疾病患者的平均年龄为 .
14.记样本、、…、的平均数为,样本、、…、的平均数为().若样本、、…、、、、…、的平均数为,则的值为 .
15.某单位有男职工30人,女职工70人,其中男职工平均年龄为40岁,方差为4,女职工平均年龄为35岁,方差是6,则该单位全体职工的方差为 .
16.某学校从全校学生中随机抽取了50名学生作为样本进行数学知识测试,记录他们的成绩,测试卷满分100分,将数据分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并整理得到如右频率分布直方图,则图中的值为 ,若全校学生参加同样的测试,估计全校学生的平均成绩为 (每组成绩用中间值代替).
四、解答题
17.自2022年动工至今,我市的“靓淮河”工程已初具规模.该工程以“一川清 两滩靓 三脉通 十景红”为总体布局,以生态修复与保护为核心理念,最终将促进城市防洪 交通 航运 生态 观光 商业等多种业态协同融合发展.为调查我市居民对“靓淮河”工程的满意程度,随机抽取了200位市民,现拟统计参与调查的市民年龄层次,将这200人按年龄(岁)分为5组,依次为,并得到频率分布直方图如下.
(1)求实数的值;
(2)估计这200人年龄的样本平均数(同一组数据用该区间的中点值作代表);
(3)估计这200人年龄的中位数(精确到小数点后1位).
18.某景点某天接待了1250名游客,老年625人,中青年500人,少年125人,该景点为了提升服务质量,采用分层抽样从当天游客中抽取100人,以评分方式进行满意度回访.将统计结果按照分成5组,制成如下频率分布直方图:
(1)求抽取的样本中,老年、中青年、少年的人数各是多少;
(2)估计当天游客满意度分值的分位数.
19.为庆祝中国共产党建党100周年,某校开展了以“学习百年党史,汇聚团结伟力”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成 A,,,,五个等级,并绘制了如图不完整的统计图. 请结合统计图,解答下列问题:
等级 成绩
(1)本次调查一共随机抽取了 名学生的成绩,频数分布直方图中 ;
(2)补全学生成绩频数分布直方图;
(3)若成绩在80分及以上为优秀,全校共有2000名学生,估计成绩优秀的学生有多少人?
20.某日数学老师进行了一次小测验,两班一共有100名学生参加了测验,成绩都在内,按照,,…,分组,得到如下频率分布直方图:
(1)求两班全体学生成绩的平均数;(每组数据以区间中点值为代表)
(2)若根据测试成绩从高到低进行排顺序,预定前40名为达标人数,估计应该把达标分数线约定为多少分.
21.文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者.某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:得到如图所示的频率分布直方图.
(1)求频率分布直方图中的值和样本成绩的四分位数;
(2)已知落在的平均成绩是65,方差是11,落在的平均成绩为75,方差是16,求两组成绩的总平均数和总方差.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据频率分布直方图直接计算即可.
【详解】由题中频率分布直方图知区间的频率为:
则在区间的频率为:,
所以第60百分位数在区间,且设为,则,
解得.
故选:B
2.D
【分析】利用平均数与方差的运算性质求解即可.
【详解】设数据,,…,的平均数和方差分别为和,
则数据,,…,的平均数为,方差为,
得,,
故选:D.
3.C
【分析】将这组数据从小到大排序,根据百分位数的概念,即可得到答案.
【详解】将这12个数据从小到大排序得:7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9,
由,可知这组数据的第25百分位数为,
由,可知这组数据的第50百分位数为,
由,可知这组数据的第75百分位数为,所以这组数据的四分位数不可能是9.9.
故选:C
4.A
【分析】根据平均数和方差的计算公式判断即可.
【详解】设该班原有位同学,中考体育成绩的平均分为,方差为,
则,,
故,,
则转来一位新同学后该班中考体育成绩的平均分为,
方差为,
故该班中考体育成绩的平均分不变,方差变小.
故选:A.
5.B
【分析】根据统计图中的数据判断即可.
【详解】由图易得A正确;
对于选项B:互联网的增长率为:;金融的增长率为:;
政府的增长率为:;电信的增长率为:;
显然金融的增长率小于电信的增长率;增长最快的不是金融行业,故B错误;
对于选项C:2021年十大行业人工智能应用渗透率的极差为,故C正确;
对于选项D:2022年十大行业人工智能应用渗透率的中位数是,故D正确.
故选:B.
6.C
【分析】根据题意,结合频率分布直方图的中位数的计算方法,即可求解.
【详解】由给定的频率分布直方图,可得前2个矩形的面积为,
前3个小矩形的面积为,
所以学生体育成绩的中位数位于之间,
设学生体育成绩的总位数为,可得分.
故选:C.
7.C
【分析】对于A,直接观察折线统计图即可判断;对于B,结合平均数的定义以及图中数据判断即可;对于C,结合百分位数的定义即可判断;对于D,无法确定农村居民与城镇居民的比例,由此即可判断.
【详解】对于A:从折线统计图可知2015年开始城镇居民的恩格尔系数均低于,
即从2015年开始进入“最富裕”水平,故A错误;
对于B:农村居民恩格尔系数只有2017 2018 2019这三年在30%到32%之间,
其余年份均大于,且2012 2013这两年大于(等于),
故农村居民恩格尔系数的平均数高于,故B错误;
对于C:城镇居民恩格尔系数从小到大排列(所对应的年份)前5位分别为2019 2018 2017 2021 2020,因为,
所以第45百分位数为第5位,即2020年的恩格尔系数,由图可知2020年的恩格尔系数高于,故C正确;
对于D:由于无法确定农村居民与城镇居民的比例,
故不能用农村居民恩格尔系数和城镇居民恩格尔系数的平均数作为全国居民恩格尔系数,故D错误.
故选:C.
8.C
【分析】分析题意,利用均值和方差的定义列方程求解即可.
【详解】设五个班级参加的人数分别为,由题意得,,分析得必定为,故,解得,或,,解得或,显然人数从低到高为,故最大值为.
故选:C
9.BCD
【分析】利用频率分布直方图中所有矩形的面积之和为,可判断A选项;计算出样本中支出在的频率,结合分层抽样可判断B选项;利用频率、频数以及样本总容量的关系可判断C选项;利用频率分布直方图计算出中位数,可判断D选项.
【详解】对于A选项,样本中支出在元的频率为,A错;
对于B选项,样本中支出在的频率为,
所以,采用分层抽样从人中抽出人,则在中共需抽出的人数为,B对;
对于C选项,,C对;
对于D选项,前两个矩形的面积之和为,
前三个矩形的面积之和为,
设样本中支出的中位数为,则,且,解得,
所以,该校学生一周生活方面支出的中位数大约是元(精确到个位数),D对.
故选:BCD.
10.BD
【分析】对A,根据条形图数据可判断;对B,根据数据计算年增长率可判断;对C,计算极差可判断;对D,根据80%分位数概念计算可判断.
【详解】对于A,根据条形图数据可以看到2020年较2019年海洋生产总值是下降的,故A错误;
对于B,2019年海洋生产总值年增长率是,
2020年海洋生产总值年增长率是,2021年海洋生产总值年增长率是,
2022年海洋生产总值年增长率是,2023年海洋生产总值年增长率是,
故年增长率最大的是2021年,故B正确;
对于C,这6年中国海洋生产总值的极差为,故C错误;
对于D,将这6年的海洋生产总值按照从小到大排列80010,83415,89415,90385,94628,98537,又,
所以这6年中国海洋生产总值的80%分位数是94628,故D正确.
故选:BD.
11.ACD
【分析】利用极差、众数、中位数、平均数的定义和性质即可求解.
【详解】由样本甲:,,,…,与样本乙:,,,…,满足,知:
样本乙的极差不等于样本甲的极差,例如样本甲:0,1,2与样本乙:,故A中结论不正确;
不妨令,
因为在上单调递减,则,
所以若某个为样本甲的中位数,则是样本乙的中位数,故B中结论正确;
因为在上单调递减,则样本乙的众数等于样本甲的众数,故C中结论不正确;
若某个为样本甲的平均数,则不一定是样本乙的平均数,
例如样本甲:0,1,2与样本乙:,故D中结论不正确.
故选:ABD.
12.BC
【分析】根据折线图得到这一星期内甲,乙的日步数,都从小到大进行排列,得到中位数后即可判断选项A;根据平均数计算公式,计算出这一星期内甲,乙的日步数的平均数,比较大小即可判断选项B;根据图象观察甲的波动程度较大,故方差较大,从而判断选项C;把乙一星期内的步数从小到大进行排列,并计算,故第六个数为所求,即可判断选项D.
【详解】由折线图可得甲一星期内的步数从小到大的排列为:
,所以中位数为12600;
由折线图可得乙一星期内的步数从小到大的排列为:
,所以中位数为12600;
故这一星期内甲、乙的日步数的中位数都为12600,A错误;
这一星期内甲的日步数的平均数为:
,
这一星期内乙的日步数的平均数为:
,
因为,故B正确;
由图知,甲的波动程度较大,故方差,标准差较大,故C正确;
乙一星期内的步数从小到大的排列为:
,故这一星期内乙的日步数的分位数是13800,故D错误.
故选:BC.
13.
【分析】根据频率分布直方图中平均数的求法求值即可.
【详解】由题意知:平均年龄(岁).
故答案为:.
14.
【分析】根据平均数公式运算求解即可.
【详解】因为样本、、…、的平均数为,可得,
样本、、…、的平均数为,可得,
又因为样本、、…、、、、…、的平均数为
,
且,整理得,即.
故答案为:.
15.10.65
【分析】利用由部分方差求总体方差的公式求解.
【详解】由题意得,该单位全体职工的平均年龄为岁,
则该单位全体职工的方差
.
故答案为:10.65
16.
【分析】由频率分布直方图中总面积为可计算出,由频率分布直方图中平均数的计算方式计算平均数即可估计全校学生的平均成绩.
【详解】由频率分布直方图中总面积为,
即,
解得,
,
故可估计全校学生的平均成绩为.
故答案为:;.
17.(1)
(2)41.5岁
(3)42.1岁
【分析】(1)根据频率之和为1,可求的值;
(2)根据频率分布直方图,可直接估算平均数;
(3)直接求频率在的数据就可估计中位数.
【详解】(1)由题意:,解得.
(2)由题意:,
估计这200人年龄的样本平均数为41.5岁.
(3)由图可知,年龄在的频率为0.25,在的频率为0.35,
,
估计这200人年龄的样本中位数为42.1岁.
18.(1)50人,40人,10人
(2)82.5
【分析】(1)求出老年、中青年、少年的人数比例,从而求抽取样本中老年、中青年、少年的人数;
(2)利用百分位数的定义进行求解即可得.
【详解】(1)老年625人,中青年500人,少年125人,
故老年、中青年、少年的人数比例为,
故抽取100人,样本中老年人数为人,
中青年人数为人,少年人数为人;
(2)设当天游客满意度分值的分位数为,
因为,
,
所以位于区间内,
则,解得:,
所以估计当天游客满意度分值的分位数为.
19.(1)200;
(2)答案见解析;
(3)
【分析】(1)根据扇形图与频率分布直方图数据计算即可;
(2)根据表格补全频率分布直方图即可;
(3)由等级D、E占比估计整体即可.
【详解】(1)根据扇形图及频率分布直方图可知B等级有40人,占总人数的20%,
则有;
(2)由(1)知等级人,补图如下:
(3)由扇形图可知成绩在80分及以上的D、E等级占比为,
所以优秀的总人数估计有人.
20.(1)99
(2)109分
【分析】(1)由所有频率和为1,列方程求出的值,由平均数公式求解即可,
(2)设分数线定为,根据频率分布直方图可知,列出方程估计录取的分线.
【详解】(1)由题意得,解得,
两班全体学生成绩的平均数为
.
(2)根据题意,达标的比例为,
设分数线定为,根据频率分布直方图可知,
则,解得,
所以估计应该把达标分数线定为109分.
21.(1),65,75,84
(2)71,38
【分析】(1)由频率分布直方图的性质即可求解;
(2)由和组的平均数和方差即可求得总平均数和总方差.
【详解】(1)利用每组小矩形的面积之和为1可得,
,解得.
四分位数分别为第25百分位数,第50百分位数,第75百分位数,
设第百分位数为,则;
设第百分位数为,则;
设第百分位数为,则;
所以该数据的四分位数分别为65,75,84.
(2)由图可知,成绩在的市民人数为,
成绩在的市民人数为,
所以;
由样本方差计算总体方差公式可得总方差为
.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
