10.3 频率与概率 同步练习(含解析)
文档属性
| 名称 | 10.3 频率与概率 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 598.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 08:11:54 | ||
图片预览




文档简介
10.3频率与概率同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.天气预报说,在今后的三天中,每一天下雨的概率均为.我们通过设计模拟实验的方法求概率,利用计算机产生之间的随机数:
425123423344144435525332152342
534443512541135432334151312354
若用1,3,5表示下雨,用2,4表示不下雨,则这三天中至少有两天下雨的概率近似为( )
A. B. C. D.
2.某学校在高三年级中抽取200名学生,调查他们课后完成作业的时间,并根据调查结果绘制了如下频率分布直方图.根据此直方图得出了下列结论,其中不正确的是( )
A.所抽取的学生中有40人在2.5小时至3小时之间完成作业
B.该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为0.1
C.估计该校高三年级学生的平均做作业的时间超过3小时
D.估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间
3.进入8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温在37摄氏度以上的概率是.用计算机生成了20组随机数,结果如下:
116 785 812 730 134 452 125 689 024 169
334 217 109 361 908 284 044 147 318 027
若用0,1,2,3,4,5表示高温橙色预警,用6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是( )
A. B. C. D.
4.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如下:
卡片号码 1 2 3 4 5 6 7 8 9 10
取到的次数 11 10 5 8 5 12 19 10 11 9
则取到号码为奇数的频率是( )
A.0.53 B.0.51 C.0.49 D.0.47
5.某商户收集并整理了2023年1月到8月线上和线下收入(单位:万元)的数据,并绘制出如图所示的折线图,则下列结论错误的是( )
A.该商户这8个月中,收入最高的是7月
B.该商户这8个月的线上总收入低于线下总收入
C.该商户这8个月中,线上、线下收入相差最小的是7月
D.该商户这8个月中,月收入不少于17万元的频率是
6.手机支付已经成为人们常用的付费方式,某大型超市为调查顾客付款方式的情况,随机抽取了100名顾客进行调查,统计结果整理如下,
顾客年龄(岁) 20岁以下 70岁及以上
手机支付人数 3 12 14 9 5 2 0
其他支付方式人数 0 0 2 13 27 12 1
从该超市顾客中随机抽取1人,估计该顾客年龄在内且未使用手机支付的概率为( )
A. B. C. D.
7.经过市场抽检,质检部门得知市场上食用油合格率为,经调查,某市市场上的食用油大约有个品牌,则不合格的食用油品牌大约有( )
A.个 B.个
C.个 D.个
8.某小区为了调查本小区业主对物业服务满意度的真实情况,对本小区业主进行了调查,调查中问了两个问题1:你的手机尾号是不是奇数?问题2:你是否满意物业的服务?调查者设计了一个随机化装置,其中装有大小、形状和质量完全相同的白球和红球,每个被调查者随机从装置中摸到红球和白球的可能性相同,其中摸到白球的业主回答第一个问题,摸到红球的业主回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不要做,由于问题的答案只有“是”和“否”,而且回答的是哪个问题别人并不知道,因此被调查者可以毫无顾虑地给出符合实际情况的答案.已知某小区80名业主参加了问卷,且有48名业主回答了“是”,由此估计本小区对物业满意服务的百分比大约为( )
A.10% B.20% C.35% D.70%
二、多选题
9.一座对外封闭的小岛上共有三座城市,三座城市第年居住人口分别为(单位万人,因为统计方法的影响,可能不为整数或有理数),假设出生率与死亡率相当(即总人口不变),每年人口都会在三座城市间流动,如城每年有留在城,有去往城,有去往城,总体流动情况如下表所示:
城市 每年去往 每年去往 每年去往
则以下说法中,正确的有( )
A.若,则
B.若三座城市人口均保持每年稳定不变,则
C.无论初始人口如何分布,经过足够久的年份后,三座城市的人口数会趋向相同
D.每两年的人口流动情况为下表所示:
城市 每两年去往 每两年去往 每两年去往
10.高中某学校对一次高三联考物理成绩进行统计分析,随机抽取100名学生成绩得到如图所示的频率分布直方图,其中分组的区间为,同时计划从样本中随机抽取个体进行随访,若从样本随机抽取个体互不影响,把频率视为概率,则下列结论正确的是( )
A.学生成绩众数估计为75分
B.考生成绩的第75百分位成绩估计为80分
C.在内随机抽取一名学生访谈,则甲被抽取的概率为0.01
D.从和内各抽1名学生,抽2名学生调研,又从他们中任取2人进行评估测试,则这2人来自不同组的概率为0.13
11.某年级组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该年级每名同学依据自己的兴趣爱好只参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加合唱社团的同学有72名,参加脱口秀社团的有120名,则该年级( )
A.参加社团的同学的总人数为480
B.参加脱口秀社团的人数占五个社团总人数的25%
C.参加朗诵社团的人数比参加舞蹈社团的多110人
D.从参加社团的同学中任选一名,其参加舞蹈或者脱口秀社团的概率为0.35
12.光明学校组建了演讲 舞蹈 航模 合唱 机器人五个社团,全校所有学生每人都参加且只参加其中一个社团,校团委在全校学生中随机选取一部分学生(这部分学生人数少于全校学生人数)进行调查,并将调查结果绘制成了如下两个不完整的统计图:则( )
A.选取的这部分学生的总人数为500人
B.合唱社团的人数占样本总量的
C.选取的学生中参加机器人社团的学生数为78人
D.选取的学生中参加合唱社团的人数比参加机器人社团人数多125
三、填空题
13.天气预报预测在今后的三天中,每天下雨的概率都为60%.现采用随机模拟的方法估计这三天中恰有两天下雨的概率,用1,2,3,4,5,6表示下雨,7,8,9,0表示不下雨.用计算机产生了10组随机数为180,792,454,417,165,809,798,386,196,206.据此估计这三天中恰有两天下雨的概率近似为 .
14.在一次男子羽毛球单打比赛中,运动员甲和乙进入了决赛(比赛采用3局2胜制),假设每局比赛甲获胜的概率为0.6,现采用随机模拟方法估计甲获得冠军的概率,先由计算机产生1~5之间的随机数,指定1,2,3表示一局比赛中甲胜,4,5表示一局比赛中乙胜 经随机模拟产生了如下20组随机数:
334 221 433 551 454 452 315 142 331 423
212 541 121 451 231 414 312 552 324 115
据此估计甲获得冠军的概率为 .
15.“键盘侠”一词描述了部分网民在现实生活中胆小怕事、自私自利,却习惯在网络上大放厥词的一种现象.某地新闻栏目对该地区群众对“键盘侠”的认可程度进行调查:在随机抽取的50人中,有14人持认可态度,其余持反对态度,若该地区有7600人,则可估计该地区对“键盘侠”持反对态度的有 人.
16.某高中学校共有学生名,各年级人数如下表,已知在全校学生中随机抽取1名学生,抽到高二年级学生的概率是.现用分层抽样的方法在全校抽取名学生,则 ,应在高三年级抽取的学生的人数为 .
年级 一年级 二年级 三年级
学生人数 1 200 x y
四、解答题
17.在某校进行男生身高调查,随机抽取100名男生,测得他们的身高(单位:),并按照区间,,,,分组,得到如下的样本数据的频率分布直方图:
(1)估计该校一位男生的身高位于区间的概率及该校男生身高的分位数;
(2)估计该校男生的平均身高(同一组数据用该区间的中点值为代表).
18.为响应垃圾分类处理,改善生态环境,某小区将生活垃圾分成三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c.并且设置了相应的垃圾箱,“厨余垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若小明将一袋分好类的生活垃圾随机投入一类垃圾箱,请写出投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了某天三类垃圾箱中总共100吨的生活垃圾,数据统计如下(单位:吨)
A B C
a 40 10 10
b 3 24 3
c 2 2 6
①请根据以上信息,试估计“厨余垃圾”投放正确的概率;
②调查发现,在“可回收垃圾”中塑料类垃圾占,每回收1吨塑料类垃圾可获得0.7吨二级原料,某城市每天大约产生2000吨生活垃圾.假设该城市对每天产生的垃圾箱中的垃圾全部分类处理,那么按样本中的投放垃圾与按规范投放垃圾相比,每月(按30天)流失掉多少吨塑料类垃圾的二级原料?
19.鲁班锁是一种广泛流传于中国民间的智力玩具,相传由春秋末期到战国初期的鲁班发明,它看似简单,却凝结着不平凡的智慧,易拆难装,十分巧妙,每根木条上的花纹是卖点,也是手工制作的关键.某玩具公司开发了甲、乙两款鲁班锁玩具,各生产了100件样品,样品分为一等品、二等品、三等品,根据销售部市场调研分析,得到相关数据如下(单件成本利润率=利润÷成本):
甲款鲁班锁玩具
一等品 二等品 三等品
单件成本利润率 10% 8% 4%
频数 10 60 30
乙款鲁班锁玩具
一等品 二等品 三等品
单件成本利润率 7.5% 5.5% 3%
频数 50 30 20
(1)用频率估计概率,从这200件产品中随机抽取一件,求该产品是一等品的概率;
(2)若甲、乙两款鲁班锁玩具的投资成本均为20000元,且每件的投资成本是相同的,分别求投资这两款鲁班锁玩具所获得的利润.
20.某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在的学生人数为6.
(1)求直方图中的值和n;
(2)试根据样本估计“该校高一学生期末数学考试成绩70”的概率.
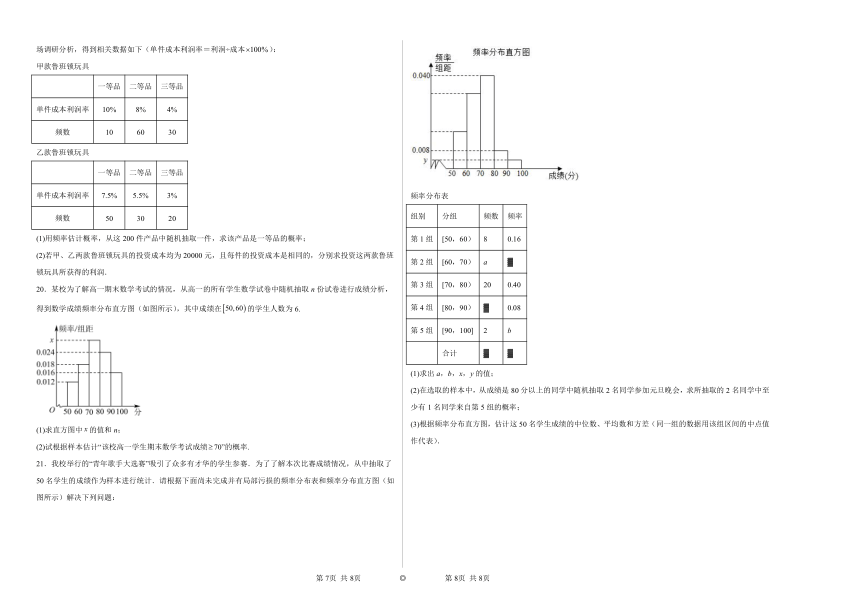
21.我校举行的“青年歌手大选赛”吸引了众多有才华的学生参赛.为了了解本次比赛成绩情况,从中抽取了50名学生的成绩作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
组别 分组 频数 频率
第1组 [50,60) 8 0.16
第2组 [60,70) a ▓
第3组 [70,80) 20 0.40
第4组 [80,90) ▓ 0.08
第5组 [90,100] 2 b
合计 ▓ ▓
(1)求出a,b,x,y的值;
(2)在选取的样本中,从成绩是80分以上的同学中随机抽取2名同学参加元旦晚会,求所抽取的2名同学中至少有1名同学来自第5组的概率;
(3)根据频率分布直方图,估计这50名学生成绩的中位数、平均数和方差(同一组的数据用该组区间的中点值作代表).
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】由样本数据,利用频率近似估计概率.
【详解】设事件“三天中至少有两天下雨”,20个随机数中,
至少有两天下雨有,
即事件发生了13次,用频率估计事件的概率近似为.
故选:D.
2.C
【分析】根据频率分布直方图结合统计、概率相关知识逐项分析判断.
【详解】对于A,在2.5小时至3小时之间的人数为人,故A正确;
对于B,该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为,故B正确;
对于C,该校高三年级学生的平均做作业的时间为
,
故C不正确;
对于D,由图可估计该校高三年级学生做作业的时间在2.5小时至4.5小时之间的频率为,
估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间,故D正确.
故选:C.
3.B
【分析】查出20个随机数中表示今后3天中恰有2天发布高温橙色预警信号的随机数的个数,根据古典概型的概率公式,即可求得答案.
【详解】由题意可知表示今后的3天中恰有2天发布高温橙色预警信号的随机数有:
116 812 730 217 109 361 284 147 318 027共10个,
故今后的3天中恰有2天发布高温橙色预警信号的概率估计是,
故选:B
4.B
【分析】运用频率定义计算即可.
【详解】由题意知,取到号码为奇数的频率为.
故选:B.
5.B
【分析】依次计算收入得到A正确,计算线下线上收入知B错误,根据图像知C正确,月收入不少于17万元的有4个月,D正确,得到答案.
【详解】对于选项A:该商户1月到8月的收入依次为16万元、13.5万元、16万元、17万元、17万元、16万元、20万元、17.5万元,A正确;
对于选项B:该商户这8个月的线上总收入为72万元,线下总收入为61万元,B错误;
对于选项C:根据折线图可知,该商户这8个月中,线上、线下收入相差最小的是7月,C正确;
对于选项D:该商户这8个月中,月收入不少于17万元的有4个月,频率为,D正确.
故选:B
6.C
【分析】根据题意求相应的频率,用频率估计概率.
【详解】由题意可知:该顾客年龄在内且未使用手机支付的频率为,
用频率估计概率,估计该顾客年龄在内且未使用手机支付的概率为.
故选:C.
7.C
【分析】先求出市场上食用油不合格率,再根据频数样本容量频率可得结果.
【详解】因为市场上食用油合格率为,所以市场上食用油不合格率为,
又市场上的食用油大约有个品牌,所以不合格的食用油品牌大约有个.
故选:C
8.D
【分析】根据问卷调查的设计原则,及两个问题被抽到、手机尾号奇数、偶数的概率分别相同,结合已知估计回答第二个问题的人数及回答“是”的人数,即可得结果.
【详解】由两个问题被问的概率相等,故约有40人回答了第一个问题,
由手机尾号为奇数和偶数的概率相等,故40人中约有20人回答“是”,
根据有48名业主回答了“是”,则约有28人在第二个问题中回答“是”,
又第二个问题被问到的人数同样约为40人,
故本小区对物业满意服务的百分比大约为.
故选:D
9.BCD
【分析】由题意知,与满足的关系式,逐项计算即可得出答案.
【详解】由题意知与满足关系式:,其中,
对于A,当,
则,则,故A错误;
对于B,在上述关系式中令,反解线性方程组,
即可知恒成立,从而,故B正确;
对于C,由流动比例的轮换对称性及总人口不变,知三座城市人口趋于相同,故C正确;
对于D,将代入,
则,故D正确.
故选:BCD.
10.AB
【分析】根据频率分布直方图估计出众数,第75百分位数可判断AB;利用频率估计概率,古典概型等知识可判断CD.
【详解】由频率分布直方图得,成绩在的频率最高,所以估计成绩的众数为75分,故A正确;
因为,所以估计第75百分位成绩为80分,故B正确;
因为成绩在内的人数为,所以随机抽取一名学生访谈,甲被抽取的概率为,故C错误;
记从抽取的1名学生为a,从抽取的1名学生为b,从抽取的2名学生为c,d,则从这4人中抽取2人,所有的可能结果为
ab,ac,ad,bc,bd,cd,共6种,
其中不同组的有ab,ac,ad,bc,bd,共5种,
所以这2人来自不同组的概率为,故D错误;
故选:AB.
11.ABD
【分析】对于A,根据参加合唱社团的人数及所占比例可求出总人数;
对于B,根据参加脱口秀社团的人数除以总人数即可判断;
对于C,求出参加朗诵社团的人数,再求出参加舞蹈社团的比例及人数即可判断;
对于D,根据参加舞蹈的占比及参加脱口秀社团的占比即可判断.
【详解】对于A,,故参加社团的同学的总人数为480,故A正确;
对于B,参加脱口秀社团的有120名,
故参加脱口秀社团的人数占五个社团总人数的,故B正确;
对于C,参加朗诵社团的人数为,
参加舞蹈社团的占比为,
参加舞蹈社团的人数为,
故参加朗诵社团的人数比参加舞蹈社团的多人,故C错误;
对于D,从参加社团的同学中任选一名,
其参加舞蹈或者脱口秀社团的概率为,即0.35,故D正确.
故选:ABD.
12.ABD
【分析】根据两个统计图表中的数据,先求出选取的总人数,然后再对选项进行逐一计算判断即可.
【详解】由两个统计图表可得参加演讲的人数为50,占选取的学生的总数的10
所以选取的总人数为人,故选项A正确.
合唱社团的人数为200人,则合唱社团的人数占样本总量的,故选B正确.
则选取的学生中参加机器人社团的人数占样本总量的
所以选取的学生中参加机器人社团的学生数为人,故选项C不正确.
选取的学生中参加合唱社团的人数为200,参加机器人社团人数为75人,
所以选取的学生中参加合唱社团的人数比参加机器人社团人数多125,选项D正确.
故选:ABD.
13./0.4
【分析】分析数据得到三天中恰有两天下雨的有417,386,196,206,得到答案.
【详解】10组随机数中,表示三天中恰有两天下雨的有417,386,196,206,
故这三天中恰有两天下雨的概率近似为.
故答案为:
14.
【分析】由13组数据表示甲获得冠军,从而估计出概率.
【详解】20组数据中,共13组数据表示甲获得冠军,
故估计甲获得冠军的概率为.
故答案为:
15.
【分析】求出在随机抽取的50人中,持反对态度的有36人,即可估计该地区对“键盘侠”持反对态度的人数.
【详解】由题意,在随机抽取的50人中,持反对态度的有36人,
故可估计该地区对“键盘侠”持反对态度的约有.
故答案为:.
16. 25
【分析】由题意得高二、高三年级学生数量,再利用分层抽样的方法能求出应在高三年级抽取的学生的人数.
【详解】由题意得高二年级学生数量为:人,
高三年级学生数量为,
现用分层抽样的方法在全校抽取100名学生,
则应在高三年级抽取的学生的人数为人.
故答案为:;.
17.(1);
(2)
【分析】(1)根据频率分布直方图利用频率估计概率运算求解,并根据百分位数的定义求分位数;
(2)直接利用平均数公式求出平均数.
【详解】(1)由题意可知:每组的频率依次为,
身高位于区间的频率为,
用频率估计概率,估计该校一位男生的身高位于区间的概率为,
又因为的人数占比为0.10,的人数占比为0.20.
可知该校100名生学身高的分位数落在.
设该校100名生学身高的分位数为x,则,解得.
故该校100名生学身高的分位数为.
(2)根据频率分布直方图,由平均数公式可得:
18.(1)
(2)①;②252
【分析】(1)列表得出所有等可能的情况数,找出垃圾投放正确的情况数,即可求出所求的概率.
(2)①利用频率估计概率求解可得.
②首先求得可回收垃圾量,然后求得二级原料即可.
【详解】(1)列表如下:
a b c
A
B
C
所有等可能的情况数有9种,
其中垃圾投放正确的有,,共3种,
所以垃圾投放正确的概率为.
(2)①.估计“厨余垃圾”投放正确的概率为,
②.由(吨),
答:每月(按30天)流失掉252吨塑料类垃圾的二级原料.
19.(1)
(2)甲鲁班锁玩具所获得的利润1400元;乙鲁班锁玩具所获得的利润1200元
【分析】(1)用频率估计概率,利用频率公式即可求;
(2)分别求出甲、乙两种鲁班锁一等品、二等品、三等品的利润,进而得到两款鲁班锁玩具所获得的利润.
【详解】(1)用频率估计概率,从这200件产品中随机抽取一件,该产品是一等品的概率为.
(2)甲款鲁班锁玩具一等品的利润为(元),
二等品的利润为(元),
三等品的利润为(元),
故100件甲款鲁班锁玩具的利润为(元).
乙款鲁班锁玩具一等品的利润为(元),
二等品的利润为(元),
三等品的利润为(元),
故100件乙款鲁班锁玩具的利润为(元).
20.(1),
(2)
【分析】(1)根据频率分布直方图的性质及频率、频数和样本容量的关系计算即可;
(2)根据样本频率估计即可.
【详解】(1)由频率分布直方图的性质得:
,解得.
∵成绩在的学生人数为6,
由频率分布直方图得成绩在的学生所占频率为:,
∴.
(2)根据样本估计“该校高一学生期末数学考试成绩70”的概率为:
.
21.(1)a=16,b=0.04,x=0.032,y=0.004
(2)
(3)中位数为70.5,平均数为70.2,方差为96.96
【分析】(1)利用频率=,及表示频率分布直方图的纵坐标即可求出a,b,x,y;
(2)由(2)可知第四组的人数,已知第五组的人数是2,利用组合的计算公式即可求出从这6人中任选2人的种数,再分两类分别求出所选的两人来自同一组的情况,利用互斥事件的概率和古典概型的概率计算公式即可得出.
(3)根据频率分布直方图,估计这50名学生成绩的中位数、平均数和方差.
【详解】(1)由题意可知,样本容量n=,
∴b==0.04,
第四组的频数=50×0.08=4,
∴.
y==0.004,x=×=0.032.
∴a=16,b=0.04,x=0.032,y=0.004.
(2)由题意可知,第4组共有4人,记为A,B,C,D,第5组共有2人,记为X,Y.
从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学,
有AB,AC,AD,BC,BD,CD,AX,AY,BX,BY,CX,CY,DX,DY,XY,共15种情况.
设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E,
有AX,AY,BX,BY,CX,CY,DX,DY,XY共9种情况.
所以随机抽取的2名同学中至少有1名同学来自第5组的概率是P(E)=.
∴随机抽取的2名同学中至少有1名同学来自第5组的概率.
(3)∵[50,70)的频率为:,
[70,80)的频率为0.4,
∴中位数为:,
平均数为:.
方差为:
.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.天气预报说,在今后的三天中,每一天下雨的概率均为.我们通过设计模拟实验的方法求概率,利用计算机产生之间的随机数:
425123423344144435525332152342
534443512541135432334151312354
若用1,3,5表示下雨,用2,4表示不下雨,则这三天中至少有两天下雨的概率近似为( )
A. B. C. D.
2.某学校在高三年级中抽取200名学生,调查他们课后完成作业的时间,并根据调查结果绘制了如下频率分布直方图.根据此直方图得出了下列结论,其中不正确的是( )
A.所抽取的学生中有40人在2.5小时至3小时之间完成作业
B.该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为0.1
C.估计该校高三年级学生的平均做作业的时间超过3小时
D.估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间
3.进入8月份后,我市持续高温,气象局一般会提前发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温在37摄氏度以上的概率是.用计算机生成了20组随机数,结果如下:
116 785 812 730 134 452 125 689 024 169
334 217 109 361 908 284 044 147 318 027
若用0,1,2,3,4,5表示高温橙色预警,用6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是( )
A. B. C. D.
4.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如下:
卡片号码 1 2 3 4 5 6 7 8 9 10
取到的次数 11 10 5 8 5 12 19 10 11 9
则取到号码为奇数的频率是( )
A.0.53 B.0.51 C.0.49 D.0.47
5.某商户收集并整理了2023年1月到8月线上和线下收入(单位:万元)的数据,并绘制出如图所示的折线图,则下列结论错误的是( )
A.该商户这8个月中,收入最高的是7月
B.该商户这8个月的线上总收入低于线下总收入
C.该商户这8个月中,线上、线下收入相差最小的是7月
D.该商户这8个月中,月收入不少于17万元的频率是
6.手机支付已经成为人们常用的付费方式,某大型超市为调查顾客付款方式的情况,随机抽取了100名顾客进行调查,统计结果整理如下,
顾客年龄(岁) 20岁以下 70岁及以上
手机支付人数 3 12 14 9 5 2 0
其他支付方式人数 0 0 2 13 27 12 1
从该超市顾客中随机抽取1人,估计该顾客年龄在内且未使用手机支付的概率为( )
A. B. C. D.
7.经过市场抽检,质检部门得知市场上食用油合格率为,经调查,某市市场上的食用油大约有个品牌,则不合格的食用油品牌大约有( )
A.个 B.个
C.个 D.个
8.某小区为了调查本小区业主对物业服务满意度的真实情况,对本小区业主进行了调查,调查中问了两个问题1:你的手机尾号是不是奇数?问题2:你是否满意物业的服务?调查者设计了一个随机化装置,其中装有大小、形状和质量完全相同的白球和红球,每个被调查者随机从装置中摸到红球和白球的可能性相同,其中摸到白球的业主回答第一个问题,摸到红球的业主回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不要做,由于问题的答案只有“是”和“否”,而且回答的是哪个问题别人并不知道,因此被调查者可以毫无顾虑地给出符合实际情况的答案.已知某小区80名业主参加了问卷,且有48名业主回答了“是”,由此估计本小区对物业满意服务的百分比大约为( )
A.10% B.20% C.35% D.70%
二、多选题
9.一座对外封闭的小岛上共有三座城市,三座城市第年居住人口分别为(单位万人,因为统计方法的影响,可能不为整数或有理数),假设出生率与死亡率相当(即总人口不变),每年人口都会在三座城市间流动,如城每年有留在城,有去往城,有去往城,总体流动情况如下表所示:
城市 每年去往 每年去往 每年去往
则以下说法中,正确的有( )
A.若,则
B.若三座城市人口均保持每年稳定不变,则
C.无论初始人口如何分布,经过足够久的年份后,三座城市的人口数会趋向相同
D.每两年的人口流动情况为下表所示:
城市 每两年去往 每两年去往 每两年去往
10.高中某学校对一次高三联考物理成绩进行统计分析,随机抽取100名学生成绩得到如图所示的频率分布直方图,其中分组的区间为,同时计划从样本中随机抽取个体进行随访,若从样本随机抽取个体互不影响,把频率视为概率,则下列结论正确的是( )
A.学生成绩众数估计为75分
B.考生成绩的第75百分位成绩估计为80分
C.在内随机抽取一名学生访谈,则甲被抽取的概率为0.01
D.从和内各抽1名学生,抽2名学生调研,又从他们中任取2人进行评估测试,则这2人来自不同组的概率为0.13
11.某年级组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该年级每名同学依据自己的兴趣爱好只参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加合唱社团的同学有72名,参加脱口秀社团的有120名,则该年级( )
A.参加社团的同学的总人数为480
B.参加脱口秀社团的人数占五个社团总人数的25%
C.参加朗诵社团的人数比参加舞蹈社团的多110人
D.从参加社团的同学中任选一名,其参加舞蹈或者脱口秀社团的概率为0.35
12.光明学校组建了演讲 舞蹈 航模 合唱 机器人五个社团,全校所有学生每人都参加且只参加其中一个社团,校团委在全校学生中随机选取一部分学生(这部分学生人数少于全校学生人数)进行调查,并将调查结果绘制成了如下两个不完整的统计图:则( )
A.选取的这部分学生的总人数为500人
B.合唱社团的人数占样本总量的
C.选取的学生中参加机器人社团的学生数为78人
D.选取的学生中参加合唱社团的人数比参加机器人社团人数多125
三、填空题
13.天气预报预测在今后的三天中,每天下雨的概率都为60%.现采用随机模拟的方法估计这三天中恰有两天下雨的概率,用1,2,3,4,5,6表示下雨,7,8,9,0表示不下雨.用计算机产生了10组随机数为180,792,454,417,165,809,798,386,196,206.据此估计这三天中恰有两天下雨的概率近似为 .
14.在一次男子羽毛球单打比赛中,运动员甲和乙进入了决赛(比赛采用3局2胜制),假设每局比赛甲获胜的概率为0.6,现采用随机模拟方法估计甲获得冠军的概率,先由计算机产生1~5之间的随机数,指定1,2,3表示一局比赛中甲胜,4,5表示一局比赛中乙胜 经随机模拟产生了如下20组随机数:
334 221 433 551 454 452 315 142 331 423
212 541 121 451 231 414 312 552 324 115
据此估计甲获得冠军的概率为 .
15.“键盘侠”一词描述了部分网民在现实生活中胆小怕事、自私自利,却习惯在网络上大放厥词的一种现象.某地新闻栏目对该地区群众对“键盘侠”的认可程度进行调查:在随机抽取的50人中,有14人持认可态度,其余持反对态度,若该地区有7600人,则可估计该地区对“键盘侠”持反对态度的有 人.
16.某高中学校共有学生名,各年级人数如下表,已知在全校学生中随机抽取1名学生,抽到高二年级学生的概率是.现用分层抽样的方法在全校抽取名学生,则 ,应在高三年级抽取的学生的人数为 .
年级 一年级 二年级 三年级
学生人数 1 200 x y
四、解答题
17.在某校进行男生身高调查,随机抽取100名男生,测得他们的身高(单位:),并按照区间,,,,分组,得到如下的样本数据的频率分布直方图:
(1)估计该校一位男生的身高位于区间的概率及该校男生身高的分位数;
(2)估计该校男生的平均身高(同一组数据用该区间的中点值为代表).
18.为响应垃圾分类处理,改善生态环境,某小区将生活垃圾分成三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c.并且设置了相应的垃圾箱,“厨余垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若小明将一袋分好类的生活垃圾随机投入一类垃圾箱,请写出投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了某天三类垃圾箱中总共100吨的生活垃圾,数据统计如下(单位:吨)
A B C
a 40 10 10
b 3 24 3
c 2 2 6
①请根据以上信息,试估计“厨余垃圾”投放正确的概率;
②调查发现,在“可回收垃圾”中塑料类垃圾占,每回收1吨塑料类垃圾可获得0.7吨二级原料,某城市每天大约产生2000吨生活垃圾.假设该城市对每天产生的垃圾箱中的垃圾全部分类处理,那么按样本中的投放垃圾与按规范投放垃圾相比,每月(按30天)流失掉多少吨塑料类垃圾的二级原料?
19.鲁班锁是一种广泛流传于中国民间的智力玩具,相传由春秋末期到战国初期的鲁班发明,它看似简单,却凝结着不平凡的智慧,易拆难装,十分巧妙,每根木条上的花纹是卖点,也是手工制作的关键.某玩具公司开发了甲、乙两款鲁班锁玩具,各生产了100件样品,样品分为一等品、二等品、三等品,根据销售部市场调研分析,得到相关数据如下(单件成本利润率=利润÷成本):
甲款鲁班锁玩具
一等品 二等品 三等品
单件成本利润率 10% 8% 4%
频数 10 60 30
乙款鲁班锁玩具
一等品 二等品 三等品
单件成本利润率 7.5% 5.5% 3%
频数 50 30 20
(1)用频率估计概率,从这200件产品中随机抽取一件,求该产品是一等品的概率;
(2)若甲、乙两款鲁班锁玩具的投资成本均为20000元,且每件的投资成本是相同的,分别求投资这两款鲁班锁玩具所获得的利润.
20.某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在的学生人数为6.
(1)求直方图中的值和n;
(2)试根据样本估计“该校高一学生期末数学考试成绩70”的概率.
21.我校举行的“青年歌手大选赛”吸引了众多有才华的学生参赛.为了了解本次比赛成绩情况,从中抽取了50名学生的成绩作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
组别 分组 频数 频率
第1组 [50,60) 8 0.16
第2组 [60,70) a ▓
第3组 [70,80) 20 0.40
第4组 [80,90) ▓ 0.08
第5组 [90,100] 2 b
合计 ▓ ▓
(1)求出a,b,x,y的值;
(2)在选取的样本中,从成绩是80分以上的同学中随机抽取2名同学参加元旦晚会,求所抽取的2名同学中至少有1名同学来自第5组的概率;
(3)根据频率分布直方图,估计这50名学生成绩的中位数、平均数和方差(同一组的数据用该组区间的中点值作代表).
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】由样本数据,利用频率近似估计概率.
【详解】设事件“三天中至少有两天下雨”,20个随机数中,
至少有两天下雨有,
即事件发生了13次,用频率估计事件的概率近似为.
故选:D.
2.C
【分析】根据频率分布直方图结合统计、概率相关知识逐项分析判断.
【详解】对于A,在2.5小时至3小时之间的人数为人,故A正确;
对于B,该校高三年级全体学生中,估计完成作业的时间超过4小时的学生概率为,故B正确;
对于C,该校高三年级学生的平均做作业的时间为
,
故C不正确;
对于D,由图可估计该校高三年级学生做作业的时间在2.5小时至4.5小时之间的频率为,
估计该校高三年级有一半的学生做作业的时间在2.5小时至4.5小时之间,故D正确.
故选:C.
3.B
【分析】查出20个随机数中表示今后3天中恰有2天发布高温橙色预警信号的随机数的个数,根据古典概型的概率公式,即可求得答案.
【详解】由题意可知表示今后的3天中恰有2天发布高温橙色预警信号的随机数有:
116 812 730 217 109 361 284 147 318 027共10个,
故今后的3天中恰有2天发布高温橙色预警信号的概率估计是,
故选:B
4.B
【分析】运用频率定义计算即可.
【详解】由题意知,取到号码为奇数的频率为.
故选:B.
5.B
【分析】依次计算收入得到A正确,计算线下线上收入知B错误,根据图像知C正确,月收入不少于17万元的有4个月,D正确,得到答案.
【详解】对于选项A:该商户1月到8月的收入依次为16万元、13.5万元、16万元、17万元、17万元、16万元、20万元、17.5万元,A正确;
对于选项B:该商户这8个月的线上总收入为72万元,线下总收入为61万元,B错误;
对于选项C:根据折线图可知,该商户这8个月中,线上、线下收入相差最小的是7月,C正确;
对于选项D:该商户这8个月中,月收入不少于17万元的有4个月,频率为,D正确.
故选:B
6.C
【分析】根据题意求相应的频率,用频率估计概率.
【详解】由题意可知:该顾客年龄在内且未使用手机支付的频率为,
用频率估计概率,估计该顾客年龄在内且未使用手机支付的概率为.
故选:C.
7.C
【分析】先求出市场上食用油不合格率,再根据频数样本容量频率可得结果.
【详解】因为市场上食用油合格率为,所以市场上食用油不合格率为,
又市场上的食用油大约有个品牌,所以不合格的食用油品牌大约有个.
故选:C
8.D
【分析】根据问卷调查的设计原则,及两个问题被抽到、手机尾号奇数、偶数的概率分别相同,结合已知估计回答第二个问题的人数及回答“是”的人数,即可得结果.
【详解】由两个问题被问的概率相等,故约有40人回答了第一个问题,
由手机尾号为奇数和偶数的概率相等,故40人中约有20人回答“是”,
根据有48名业主回答了“是”,则约有28人在第二个问题中回答“是”,
又第二个问题被问到的人数同样约为40人,
故本小区对物业满意服务的百分比大约为.
故选:D
9.BCD
【分析】由题意知,与满足的关系式,逐项计算即可得出答案.
【详解】由题意知与满足关系式:,其中,
对于A,当,
则,则,故A错误;
对于B,在上述关系式中令,反解线性方程组,
即可知恒成立,从而,故B正确;
对于C,由流动比例的轮换对称性及总人口不变,知三座城市人口趋于相同,故C正确;
对于D,将代入,
则,故D正确.
故选:BCD.
10.AB
【分析】根据频率分布直方图估计出众数,第75百分位数可判断AB;利用频率估计概率,古典概型等知识可判断CD.
【详解】由频率分布直方图得,成绩在的频率最高,所以估计成绩的众数为75分,故A正确;
因为,所以估计第75百分位成绩为80分,故B正确;
因为成绩在内的人数为,所以随机抽取一名学生访谈,甲被抽取的概率为,故C错误;
记从抽取的1名学生为a,从抽取的1名学生为b,从抽取的2名学生为c,d,则从这4人中抽取2人,所有的可能结果为
ab,ac,ad,bc,bd,cd,共6种,
其中不同组的有ab,ac,ad,bc,bd,共5种,
所以这2人来自不同组的概率为,故D错误;
故选:AB.
11.ABD
【分析】对于A,根据参加合唱社团的人数及所占比例可求出总人数;
对于B,根据参加脱口秀社团的人数除以总人数即可判断;
对于C,求出参加朗诵社团的人数,再求出参加舞蹈社团的比例及人数即可判断;
对于D,根据参加舞蹈的占比及参加脱口秀社团的占比即可判断.
【详解】对于A,,故参加社团的同学的总人数为480,故A正确;
对于B,参加脱口秀社团的有120名,
故参加脱口秀社团的人数占五个社团总人数的,故B正确;
对于C,参加朗诵社团的人数为,
参加舞蹈社团的占比为,
参加舞蹈社团的人数为,
故参加朗诵社团的人数比参加舞蹈社团的多人,故C错误;
对于D,从参加社团的同学中任选一名,
其参加舞蹈或者脱口秀社团的概率为,即0.35,故D正确.
故选:ABD.
12.ABD
【分析】根据两个统计图表中的数据,先求出选取的总人数,然后再对选项进行逐一计算判断即可.
【详解】由两个统计图表可得参加演讲的人数为50,占选取的学生的总数的10
所以选取的总人数为人,故选项A正确.
合唱社团的人数为200人,则合唱社团的人数占样本总量的,故选B正确.
则选取的学生中参加机器人社团的人数占样本总量的
所以选取的学生中参加机器人社团的学生数为人,故选项C不正确.
选取的学生中参加合唱社团的人数为200,参加机器人社团人数为75人,
所以选取的学生中参加合唱社团的人数比参加机器人社团人数多125,选项D正确.
故选:ABD.
13./0.4
【分析】分析数据得到三天中恰有两天下雨的有417,386,196,206,得到答案.
【详解】10组随机数中,表示三天中恰有两天下雨的有417,386,196,206,
故这三天中恰有两天下雨的概率近似为.
故答案为:
14.
【分析】由13组数据表示甲获得冠军,从而估计出概率.
【详解】20组数据中,共13组数据表示甲获得冠军,
故估计甲获得冠军的概率为.
故答案为:
15.
【分析】求出在随机抽取的50人中,持反对态度的有36人,即可估计该地区对“键盘侠”持反对态度的人数.
【详解】由题意,在随机抽取的50人中,持反对态度的有36人,
故可估计该地区对“键盘侠”持反对态度的约有.
故答案为:.
16. 25
【分析】由题意得高二、高三年级学生数量,再利用分层抽样的方法能求出应在高三年级抽取的学生的人数.
【详解】由题意得高二年级学生数量为:人,
高三年级学生数量为,
现用分层抽样的方法在全校抽取100名学生,
则应在高三年级抽取的学生的人数为人.
故答案为:;.
17.(1);
(2)
【分析】(1)根据频率分布直方图利用频率估计概率运算求解,并根据百分位数的定义求分位数;
(2)直接利用平均数公式求出平均数.
【详解】(1)由题意可知:每组的频率依次为,
身高位于区间的频率为,
用频率估计概率,估计该校一位男生的身高位于区间的概率为,
又因为的人数占比为0.10,的人数占比为0.20.
可知该校100名生学身高的分位数落在.
设该校100名生学身高的分位数为x,则,解得.
故该校100名生学身高的分位数为.
(2)根据频率分布直方图,由平均数公式可得:
18.(1)
(2)①;②252
【分析】(1)列表得出所有等可能的情况数,找出垃圾投放正确的情况数,即可求出所求的概率.
(2)①利用频率估计概率求解可得.
②首先求得可回收垃圾量,然后求得二级原料即可.
【详解】(1)列表如下:
a b c
A
B
C
所有等可能的情况数有9种,
其中垃圾投放正确的有,,共3种,
所以垃圾投放正确的概率为.
(2)①.估计“厨余垃圾”投放正确的概率为,
②.由(吨),
答:每月(按30天)流失掉252吨塑料类垃圾的二级原料.
19.(1)
(2)甲鲁班锁玩具所获得的利润1400元;乙鲁班锁玩具所获得的利润1200元
【分析】(1)用频率估计概率,利用频率公式即可求;
(2)分别求出甲、乙两种鲁班锁一等品、二等品、三等品的利润,进而得到两款鲁班锁玩具所获得的利润.
【详解】(1)用频率估计概率,从这200件产品中随机抽取一件,该产品是一等品的概率为.
(2)甲款鲁班锁玩具一等品的利润为(元),
二等品的利润为(元),
三等品的利润为(元),
故100件甲款鲁班锁玩具的利润为(元).
乙款鲁班锁玩具一等品的利润为(元),
二等品的利润为(元),
三等品的利润为(元),
故100件乙款鲁班锁玩具的利润为(元).
20.(1),
(2)
【分析】(1)根据频率分布直方图的性质及频率、频数和样本容量的关系计算即可;
(2)根据样本频率估计即可.
【详解】(1)由频率分布直方图的性质得:
,解得.
∵成绩在的学生人数为6,
由频率分布直方图得成绩在的学生所占频率为:,
∴.
(2)根据样本估计“该校高一学生期末数学考试成绩70”的概率为:
.
21.(1)a=16,b=0.04,x=0.032,y=0.004
(2)
(3)中位数为70.5,平均数为70.2,方差为96.96
【分析】(1)利用频率=,及表示频率分布直方图的纵坐标即可求出a,b,x,y;
(2)由(2)可知第四组的人数,已知第五组的人数是2,利用组合的计算公式即可求出从这6人中任选2人的种数,再分两类分别求出所选的两人来自同一组的情况,利用互斥事件的概率和古典概型的概率计算公式即可得出.
(3)根据频率分布直方图,估计这50名学生成绩的中位数、平均数和方差.
【详解】(1)由题意可知,样本容量n=,
∴b==0.04,
第四组的频数=50×0.08=4,
∴.
y==0.004,x=×=0.032.
∴a=16,b=0.04,x=0.032,y=0.004.
(2)由题意可知,第4组共有4人,记为A,B,C,D,第5组共有2人,记为X,Y.
从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学,
有AB,AC,AD,BC,BD,CD,AX,AY,BX,BY,CX,CY,DX,DY,XY,共15种情况.
设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E,
有AX,AY,BX,BY,CX,CY,DX,DY,XY共9种情况.
所以随机抽取的2名同学中至少有1名同学来自第5组的概率是P(E)=.
∴随机抽取的2名同学中至少有1名同学来自第5组的概率.
(3)∵[50,70)的频率为:,
[70,80)的频率为0.4,
∴中位数为:,
平均数为:.
方差为:
.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
