第八章 数据的收集与整理 3 数据的表示 第2课时 频数直方图(含答案)
文档属性
| 名称 | 第八章 数据的收集与整理 3 数据的表示 第2课时 频数直方图(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 09:13:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章 数据的收集与整理
3 数据的表示
第2课时 频数直方图
1.将 100个数据分成8个组,如表,则第6 组的频数为 ( )
组号 1 2 3 4 5 6 7 8
频数 11 14 12 13 13 12 10
A.12 B.13 C.14 D.15
2.已知样本的数据个数为30,且被分成 4 组,第一组至第四组的数据个数之比为 2:4:3:1,则第二组、第三组的数据频数分别为 ( )
A.4,3 B.8,6 C.12,9 D.9,12
3.某校九(1)班 50 名学生的视力频数直方图如图所示,(每一组含前一个边界值,不含后一个边界值),若视力达到4.8以上(含4.8)为达标,则该班学生视力的达标率为( )
九(1)班50名学生视力频数直方图
A.8% B.18% C.29% D.36%
4.某次数学测试,抽取部分同学的成绩(得分为整数),整理制成如图所示的频数分布直方图,根据图示信息描述不正确的是 ( )
A.频数分布直方图中组距是 10 B.本次抽样样本容量是 60
C.70.5~80.5 这一分数段的频数为 18 D.这次测试及格(不低于 60分)率92%以上
5.为了解某校学生的身高情况,随机抽取该校男生女生进行抽样调查,已知抽取的样本中,男生女生的人数相同,利用所得数据,绘制如下统计图表:
身高情况分组表(单位:cm)
组别 A B C D E
身高
男生身高情况直方图 女生身高情况扇形统计图
根据图表提供的信息样本中,身高在 之间的女生人数为 ( )
A.6 B.8 C.10 D.16
6.某检测收到 40 个数据,其中最大值为 35,最小值为 14,画频数分布直方图时,如果取组距为 4,那么应分成____________组.
7.6月6日是全国爱眼日,某校对七年级学生进行了视力监测,收集了部分学生的监测数据,并绘制成了频数分布直方图,从左至右每个小长方形的高的比为 1:4:3:2,其中第三组的频数为 45,则共收集了____________名学生的监测数据.
8.某校学生“亚运知识”竞赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在80 分及以上的学生有__________人.
某校学生“亚运知识”竞赛成绩的频数直方图
9.2023 年 5 月 30 日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有 100 件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图,则a的值为____________.若将获奖作品按四个等级所占比例绘制成扇形统计图,则“一等奖”对应扇形的圆心角度数为______________.
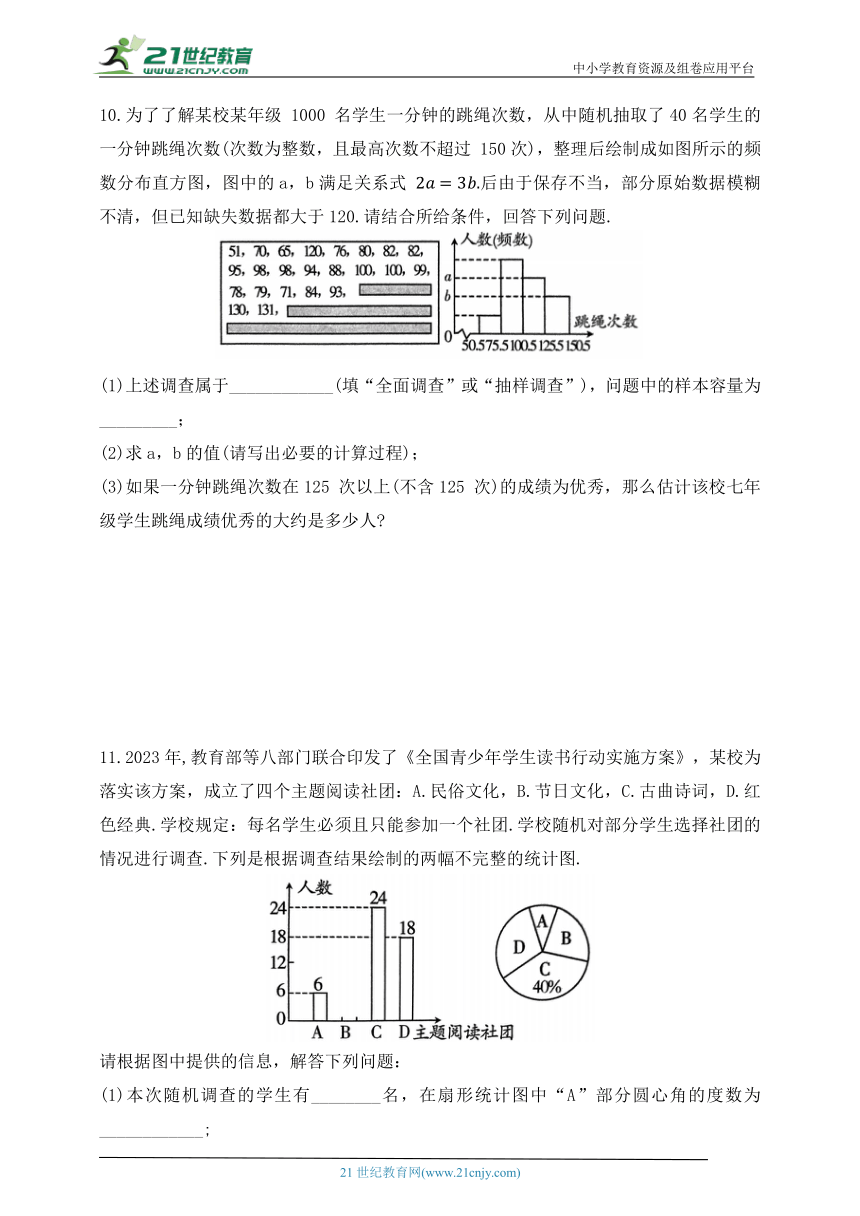
10.为了了解某校某年级 1000 名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过 150次),整理后绘制成如图所示的频数分布直方图,图中的a,b满足关系式 后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题.
(1)上述调查属于____________(填“全面调查”或“抽样调查”),问题中的样本容量为_________;
(2)求a,b的值(请写出必要的计算过程);
(3)如果一分钟跳绳次数在125 次以上(不含125 次)的成绩为优秀,那么估计该校七年级学生跳绳成绩优秀的大约是多少人
11.2023年,教育部等八部门联合印发了《全国青少年学生读书行动实施方案》,某校为落实该方案,成立了四个主题阅读社团:A.民俗文化,B.节日文化,C.古曲诗词,D.红色经典.学校规定:每名学生必须且只能参加一个社团.学校随机对部分学生选择社团的情况进行调查.下列是根据调查结果绘制的两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)本次随机调查的学生有________名,在扇形统计图中“A”部分圆心角的度数为____________;
(2)通过计算补全条形统计图;
(3)若该校共有 1 800 名学生,请根据以上调查结果,估计全校参加“D”社团的人数.
12.“校园诗词大赛”结束后,老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别制成扇形统计图和频数直方图如图:
(1)本次比赛的选手共________人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为__________;
(2)将频数直方图补充完整;
(3)规定:成绩由高到低前 60%的选手可获奖,小明比赛成绩为 78 分,判断他能否获奖,并说明理由.
13.举世瞩目的中国共产党第二十次全国代表大会于 2022 年 10 月在北京成功召开.为弘扬党的二十大精神,某学校举办了“学习二十大,奋进新征程”的知识竞赛活动.赛后随机抽取了部分学生的成绩(满分:100 分),分为 A,B,C,D四组,绘制了下列不完整的统计图表:
组别 成绩(/分) 频数
学生成绩频数分布直方图 学生成绩扇形统计图
根据以上信息,解答以下问题:
(1)直接写出统计表中的
(2)在学生成绩扇形统计图中,B组对应的扇形圆心角α是__________°;
(3)将学生成绩频数分布直方图补充完整;
(4)若全校有 1 500 名学生参加了这次竞赛,请估计成绩高于 90分的学生人数.
参考答案
1. D 2. C 3. D 4. B 5. A
6. 6 7. 150 8. 140 9.30 36°
10.解:(1)抽样调查,40;
(2)由题意所给数据可知 50.5~75. 5 的有4 人,75.5~100.5 的有 16 人,
所以 因为 解得
(人),
答:该校七年级学生跳绳成绩优秀的大约是200 人.
11.解:(1) 本 次 调查 的 总人 数 为 60(名),
扇形统计图中,A 所对应的扇形的圆心角度数是
故答案为:60,36°;
(2)60-6-24-18=12(人),
补全条形统计图如图所示:
(名).
答:全校1 800名学生中,参加“D”社团的学生约有 540 名.
12.解:(1)本次比赛的选手共( 50(人),
扇形统计图中“79.5~89.5”这一组人数! 人,
扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为
故答案为:50,30%;
(2)条形统计图中“84.5~89.5”这一组人数为 (人),
条形统计图中“69.5~74.5”这一组人数为50-2-3-8-10-8-8-4=7(人),
补全频数直方图,如图所示:
(3)不能获奖,理由如下:
因为“79.5~99.5”共 30人,占总数60%,前60%才可获奖,所以他不能获奖.
13.解:(1)由题意知,共调查 (人), 所以 (人),
所以m=200-20-60-80=40(人),故答案为:40,80;
故答案为:72;
(3)补全条形统计图如图:
(4)因为 (人),
所以成绩高于 90分的学生人数约为 1050人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 数据的收集与整理
3 数据的表示
第2课时 频数直方图
1.将 100个数据分成8个组,如表,则第6 组的频数为 ( )
组号 1 2 3 4 5 6 7 8
频数 11 14 12 13 13 12 10
A.12 B.13 C.14 D.15
2.已知样本的数据个数为30,且被分成 4 组,第一组至第四组的数据个数之比为 2:4:3:1,则第二组、第三组的数据频数分别为 ( )
A.4,3 B.8,6 C.12,9 D.9,12
3.某校九(1)班 50 名学生的视力频数直方图如图所示,(每一组含前一个边界值,不含后一个边界值),若视力达到4.8以上(含4.8)为达标,则该班学生视力的达标率为( )
九(1)班50名学生视力频数直方图
A.8% B.18% C.29% D.36%
4.某次数学测试,抽取部分同学的成绩(得分为整数),整理制成如图所示的频数分布直方图,根据图示信息描述不正确的是 ( )
A.频数分布直方图中组距是 10 B.本次抽样样本容量是 60
C.70.5~80.5 这一分数段的频数为 18 D.这次测试及格(不低于 60分)率92%以上
5.为了解某校学生的身高情况,随机抽取该校男生女生进行抽样调查,已知抽取的样本中,男生女生的人数相同,利用所得数据,绘制如下统计图表:
身高情况分组表(单位:cm)
组别 A B C D E
身高
男生身高情况直方图 女生身高情况扇形统计图
根据图表提供的信息样本中,身高在 之间的女生人数为 ( )
A.6 B.8 C.10 D.16
6.某检测收到 40 个数据,其中最大值为 35,最小值为 14,画频数分布直方图时,如果取组距为 4,那么应分成____________组.
7.6月6日是全国爱眼日,某校对七年级学生进行了视力监测,收集了部分学生的监测数据,并绘制成了频数分布直方图,从左至右每个小长方形的高的比为 1:4:3:2,其中第三组的频数为 45,则共收集了____________名学生的监测数据.
8.某校学生“亚运知识”竞赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在80 分及以上的学生有__________人.
某校学生“亚运知识”竞赛成绩的频数直方图
9.2023 年 5 月 30 日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有 100 件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图,则a的值为____________.若将获奖作品按四个等级所占比例绘制成扇形统计图,则“一等奖”对应扇形的圆心角度数为______________.
10.为了了解某校某年级 1000 名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过 150次),整理后绘制成如图所示的频数分布直方图,图中的a,b满足关系式 后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题.
(1)上述调查属于____________(填“全面调查”或“抽样调查”),问题中的样本容量为_________;
(2)求a,b的值(请写出必要的计算过程);
(3)如果一分钟跳绳次数在125 次以上(不含125 次)的成绩为优秀,那么估计该校七年级学生跳绳成绩优秀的大约是多少人
11.2023年,教育部等八部门联合印发了《全国青少年学生读书行动实施方案》,某校为落实该方案,成立了四个主题阅读社团:A.民俗文化,B.节日文化,C.古曲诗词,D.红色经典.学校规定:每名学生必须且只能参加一个社团.学校随机对部分学生选择社团的情况进行调查.下列是根据调查结果绘制的两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)本次随机调查的学生有________名,在扇形统计图中“A”部分圆心角的度数为____________;
(2)通过计算补全条形统计图;
(3)若该校共有 1 800 名学生,请根据以上调查结果,估计全校参加“D”社团的人数.
12.“校园诗词大赛”结束后,老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别制成扇形统计图和频数直方图如图:
(1)本次比赛的选手共________人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为__________;
(2)将频数直方图补充完整;
(3)规定:成绩由高到低前 60%的选手可获奖,小明比赛成绩为 78 分,判断他能否获奖,并说明理由.
13.举世瞩目的中国共产党第二十次全国代表大会于 2022 年 10 月在北京成功召开.为弘扬党的二十大精神,某学校举办了“学习二十大,奋进新征程”的知识竞赛活动.赛后随机抽取了部分学生的成绩(满分:100 分),分为 A,B,C,D四组,绘制了下列不完整的统计图表:
组别 成绩(/分) 频数
学生成绩频数分布直方图 学生成绩扇形统计图
根据以上信息,解答以下问题:
(1)直接写出统计表中的
(2)在学生成绩扇形统计图中,B组对应的扇形圆心角α是__________°;
(3)将学生成绩频数分布直方图补充完整;
(4)若全校有 1 500 名学生参加了这次竞赛,请估计成绩高于 90分的学生人数.
参考答案
1. D 2. C 3. D 4. B 5. A
6. 6 7. 150 8. 140 9.30 36°
10.解:(1)抽样调查,40;
(2)由题意所给数据可知 50.5~75. 5 的有4 人,75.5~100.5 的有 16 人,
所以 因为 解得
(人),
答:该校七年级学生跳绳成绩优秀的大约是200 人.
11.解:(1) 本 次 调查 的 总人 数 为 60(名),
扇形统计图中,A 所对应的扇形的圆心角度数是
故答案为:60,36°;
(2)60-6-24-18=12(人),
补全条形统计图如图所示:
(名).
答:全校1 800名学生中,参加“D”社团的学生约有 540 名.
12.解:(1)本次比赛的选手共( 50(人),
扇形统计图中“79.5~89.5”这一组人数! 人,
扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为
故答案为:50,30%;
(2)条形统计图中“84.5~89.5”这一组人数为 (人),
条形统计图中“69.5~74.5”这一组人数为50-2-3-8-10-8-8-4=7(人),
补全频数直方图,如图所示:
(3)不能获奖,理由如下:
因为“79.5~99.5”共 30人,占总数60%,前60%才可获奖,所以他不能获奖.
13.解:(1)由题意知,共调查 (人), 所以 (人),
所以m=200-20-60-80=40(人),故答案为:40,80;
故答案为:72;
(3)补全条形统计图如图:
(4)因为 (人),
所以成绩高于 90分的学生人数约为 1050人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
