第八章 二元一次方程组 消元法2
文档属性
| 名称 | 第八章 二元一次方程组 消元法2 |  | |
| 格式 | rar | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-31 18:52:00 | ||
图片预览





文档简介
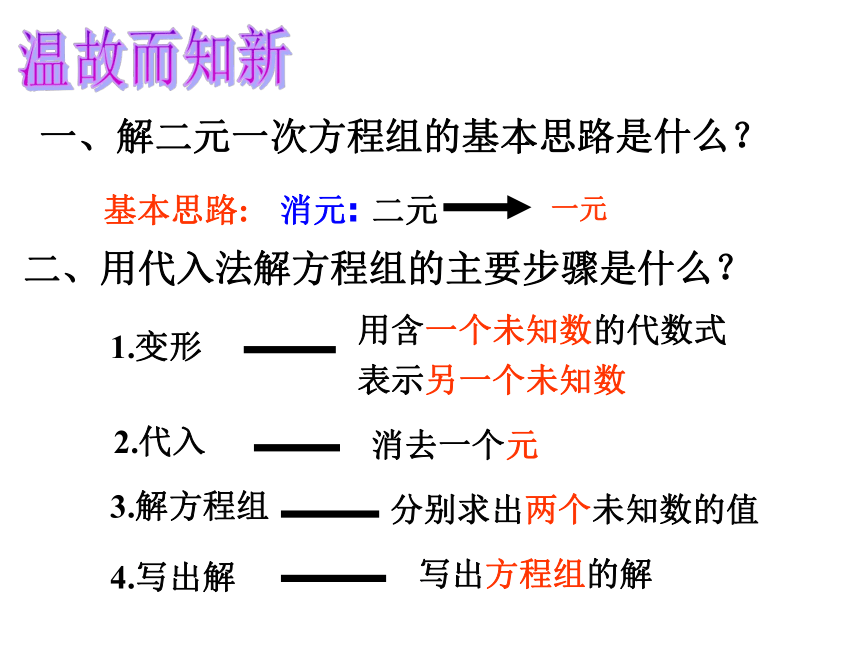
课件14张PPT。8.2 消 元(2)一、解二元一次方程组的基本思路是什么?二、用代入法解方程组的主要步骤是什么?温故而知新观察:④与原方程组之间有什么联系?有没有更加简便的方法求得④问题引入怎样解下面的二元一次方程组呢?② 左边 - ① 左边 = ② 右边 - ① 右边(等式的性质)①②由此可得,②-①得归纳规律:当同一未知数的系数相同时,把两个方程两边分别相减, 就能消去这个未知数.举一反三思考:联系上面解法,想一想怎样解下面这个方程组①+②,得归纳规律:当同一未知数的系数相反时,把两个方程两边分别相加,就能消去这个未知数.归纳总结:
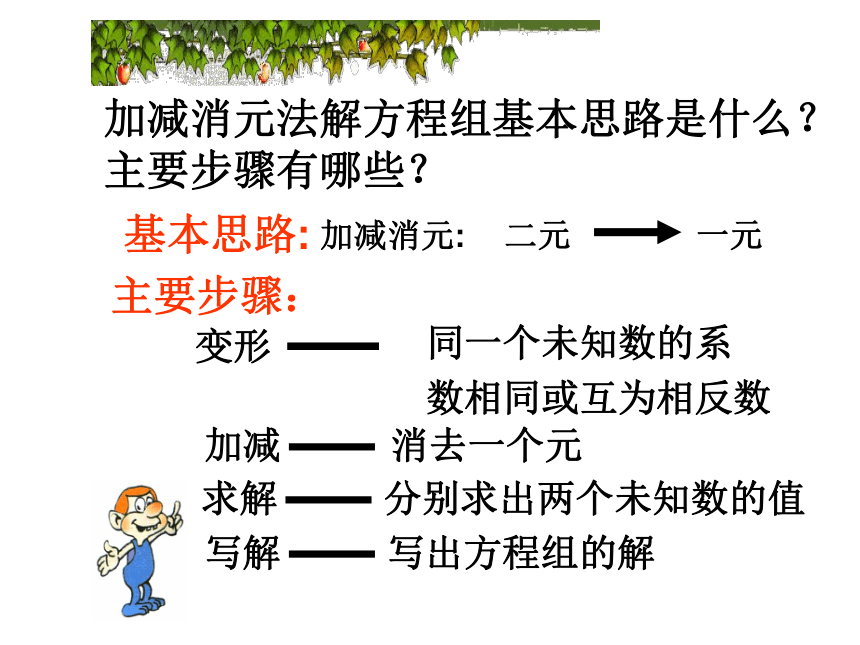
两个二元一次方程中同一个未知数的系数相反或相同时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法. 例3用加减法解方程组:解:①×3得 9x+12y=48③③+④得 19x=114
x=6②×2得 10x-12y=66④思考:用加减法先消去未知数x该如何解?解得的结果与左面的解相同吗?把x=6代入① 得: y=-解: ①×5得15x+20y= 80③②×3得 15x - 18y = 99④③-④得 38y=-19
x=把y = 代入① 得: x=6 所以这个方程组的解是基本思路:主要步骤:加减消元:加减消元法解方程组基本思路是什么?主要步骤有哪些?1、用加减法解下列方程组;反馈练习⑴⑵⑷⑶123解:由①+②得: 4x = 8
x = 2
把x=2代入①,得: y=
所以这个方程组的解是:①②4把x = 5 代入①得
所以这个方程组的解是:3x+2× =5
x=⑶①②所以这个方程组的解是⑷①②解:①×2,得 4x+6y=12③②×3,得 9x-6y=-6④③+④,得13x=6
x=把x= 代入①,得2× + 3y = 6
y =所以这个方程组的解是 结合上一节课的内容如何适当的选用代入消元法和加减消元法解二元一次方程组,能让解题的过程更加简单?思考归纳1、当方程组中某个未知数的系数为±1或常数项为0时,用代入法解方程组比较简单。2、当方程组中相同的未知数的系数相同或互为相反数时,直接加减消元:反之则用适当的数乘方程的两边,使两个方程中的同一个未知数的系数相等或相反,再加减。加减消元法:两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,小结:学习了本节课你有哪些 收获?加减消元法解方程组的主要步骤: 1.P103
习题第3题
作 业
两个二元一次方程中同一个未知数的系数相反或相同时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法. 例3用加减法解方程组:解:①×3得 9x+12y=48③③+④得 19x=114
x=6②×2得 10x-12y=66④思考:用加减法先消去未知数x该如何解?解得的结果与左面的解相同吗?把x=6代入① 得: y=-解: ①×5得15x+20y= 80③②×3得 15x - 18y = 99④③-④得 38y=-19
x=把y = 代入① 得: x=6 所以这个方程组的解是基本思路:主要步骤:加减消元:加减消元法解方程组基本思路是什么?主要步骤有哪些?1、用加减法解下列方程组;反馈练习⑴⑵⑷⑶123解:由①+②得: 4x = 8
x = 2
把x=2代入①,得: y=
所以这个方程组的解是:①②4把x = 5 代入①得
所以这个方程组的解是:3x+2× =5
x=⑶①②所以这个方程组的解是⑷①②解:①×2,得 4x+6y=12③②×3,得 9x-6y=-6④③+④,得13x=6
x=把x= 代入①,得2× + 3y = 6
y =所以这个方程组的解是 结合上一节课的内容如何适当的选用代入消元法和加减消元法解二元一次方程组,能让解题的过程更加简单?思考归纳1、当方程组中某个未知数的系数为±1或常数项为0时,用代入法解方程组比较简单。2、当方程组中相同的未知数的系数相同或互为相反数时,直接加减消元:反之则用适当的数乘方程的两边,使两个方程中的同一个未知数的系数相等或相反,再加减。加减消元法:两个二元一次方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,小结:学习了本节课你有哪些 收获?加减消元法解方程组的主要步骤: 1.P103
习题第3题
作 业
