7.4 正切函数的图像与性质 教学设计
文档属性
| 名称 | 7.4 正切函数的图像与性质 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 272.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 21:23:46 | ||
图片预览



文档简介
《正切函数的图像与性质》教学设计
一、教学目标
1、理解正切函数的定义及正切函数的图像特征,研究并掌握正切函数的基本性质。
2、在探究正切函数基本性质和图像的过程中,体验类比、数形结合等数学思想方法。
3、养成严谨的思维习惯,逐步提高逻辑推理、直观想象的核心素养。
二、教学重点 正切函数的图像与基本性质
三、教学难点 正切函数的最小正周期的理解 正切函数单调性的认识
四、核心知识 核心概念:正切函数的定义
核心方法:类比研究正切函数性质的思维方法
核心思想:研究函数性质中数形结合的思想方法
核心素养:逻辑推理、直观想象的核心素养
五、教学方法 探究体验、合作学习
六、教学流程图
教师:创设问题情境 启发探求思路 多元评价 理性概括
程序:
学生:接受问题挑战 自主探究 汇报交流 自主构建
七、教学过程
(一)、设置疑问,引入新课
1、正切函数的定义
对下列给出的正切函数的概念作比较,在比较中掌握正切函数的概念。
有同学,类比正弦函数、余弦函数的定义,定义了一个正切函数:
对于任意一个实数,都有唯一确定的值与它对应,按照这个对应法则所建立的函数,表示为,叫做正切函数.
大家认为这个定义是否完善? 强调:.
设计意图:,是学生容易出错的地方,通过学生之间的自我纠错,理解不能取的理由)。
今天我们就要研究正切函数()的图像与性质.
2、(前面)我们是怎样研究正弦函数的图像与性质的?
前面,我们在研究正弦函数的图像与性质是先作出正弦函数的图像,然后再由图像得到它的性质。今天,我们想改变一种研究的思路,即:先研究它的性质,然后在作它的图像。
(二)、主动探究,学习新知
1、利用定义,研究函数的性质 (学生自主研究探索正切函数的性质)
性质(1)定义域:.
性质(2)值域:R
说明:利用正切线得到正切函数的值域。
性质(3)奇偶性:奇函数.
说明:利用奇函数的定义得出结论。
性质(4)周期性:是最小正周期.
说明:学生会利用,得到是函数的周期后教师提问:能否说明是最小正周期? 引导学生思考能否利用周期函数的定义证明呢?(留作课后思考)
反证法:假设存在是的周期,
则都有.
取,则..,这与矛盾.从而,是正切函数的最小正周期.
我们已经知道了正切函数的一些基本性质,根据这些性质,你能勾画出正切函数的大致图像吗?
(三)结合性质,作出函数的图像
(1)自变量区间的选择。
说明:学生可能会作出下列的选择。
a、按周期选择、等;
b、按奇偶性选择。
根据学生的选择教师引导学生讨论,自变量区间的选择最好保证能够作出较为完整的图像,最后形成统一认识。
(2)利用计算器让学生感受正切函数的变化特点。
(3)借助于正切线,学生自主画出正切函数在上的图像。
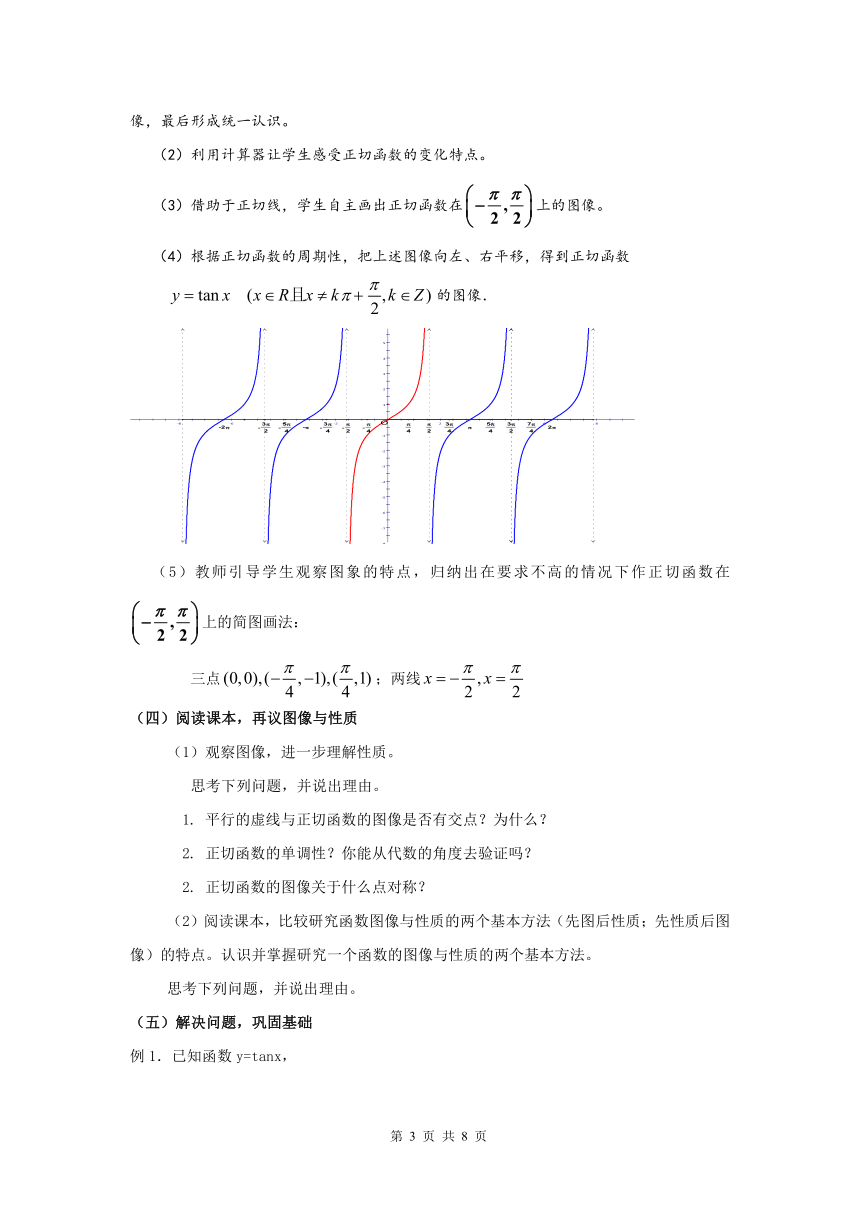
(4)根据正切函数的周期性,把上述图像向左、右平移,得到正切函数
的图像.
(5)教师引导学生观察图象的特点,归纳出在要求不高的情况下作正切函数在上的简图画法:
三点;两线
(四)阅读课本,再议图像与性质
(1)观察图像,进一步理解性质。
思考下列问题,并说出理由。
1. 平行的虚线与正切函数的图像是否有交点?为什么?
2. 正切函数的单调性?你能从代数的角度去验证吗?
2. 正切函数的图像关于什么点对称?
(2)阅读课本,比较研究函数图像与性质的两个基本方法(先图后性质;先性质后图像)的特点。认识并掌握研究一个函数的图像与性质的两个基本方法。
思考下列问题,并说出理由。
(五)解决问题,巩固基础
例1.已知函数y=tanx,
(1)若,求y的取值范围;(2)若,求y的取值范围.
说明:
利用函数在区间上单调递增得到答案.
把y=tanx在区间上的图像不断向左、右扩展,也可得到正切函数的图像.因此, 有同学说正切函数在一个周期上递增是错误的.也可以对照说明,作正切函数图时选择的合理性.
例2.写出使不等式成立的x的集合.
说明:先求在上满足条件的,然后扩展到整个定义域.函数图像是函数的一种表达形式,形象地显示了函数的性质,为研究数量关系提供了“形”的直观性.它是探求解题途径,获得问题结果的重要工具,通过例题提醒学生重视数形结合的思想方法.
例3、研究函数的基本性质. 改为呢?
说明:大多数同学能够掌握的图像可以通过的图像向左平移个单位得到,从而方便地结合图像研究性质.
研究的性质要困难的多.希望同学能类比研究正弦、余弦函数时的方法解决,必要时通过代换来解决.
(六)总结思考,提高能力
学生交流在本节课学习中的体会、收获,交流学习过程中的体验和感受,师生合作共同完成小结.
(1) 理解了正切函数的定义;理解了正切函数的图像特征;掌握了正切函数的基本性质.
(2)运用了举反例、类比、反证法等数学方法,体会了数形结合的思想.
(七)分层作业,巩固拓展
1、全体同学完成课本95页第4、5题.
2、每位同学结合今天研究的内容,设计一道回家作业题,并选择下列问题中的1——2个问题进行研究。
(1)函数和是同一个函数吗?
(2)研究函数的基本性质.
(3)研究函数的基本性质,作出大致图像.
(4)联想祖暅原理,我们得到:“夹在两条平行线间的两个平面图形,被平行于这两条平行线的任意一条直线所截,如果截得的两条线段的长相等,那么这两个平面图形的面积相等。”请研究下列问题:设函数,请求出和与两条直线所围成的平面图形的面积。
附件一 《正切函数的图像与性质》学习任务工作单
一、学习任务
1、理解正切函数的定义及正切函数的图像特征,研究并掌握正切函数的基本性质。
2、在探究正切函数基本性质和图像的过程中,体验类比、数形结合等数学的思想方法。
3、养成严谨的思维习惯,逐步提高自己发现问题、提出问题、解决问题的能力。
二、任务学习
(一)概念学习:
正弦函数的概念:对于任意一个给定的实数 ,都有唯一确定的正弦值 sin 与之对应. 按
照这个对应关系所建立的函数叫做正弦函数,记作 =sin .
正切函数的概念
(二)正切函数的图像与性质的探究
序号 性质名称
1 定义域
2 值 域
3 最 值
4 奇偶性
5 周期性
6 单调性
7
8
(三)问题研究
例1.已知函数y=tanx,
(1)若,求y的取值范围;(2)若,求y的取值范围.
例2.写出使不等式成立的x的集合.
例3、研究函数的基本性质.
(四)小结交流 (思考今天的学习任务,将收获与同学交流。)
(五)拓展训练
1、完成课本95页第4、5题.
2、结合今天研究的内容,设计一道回家作业题,并选择下列问题中的1——2个问题进行研究。
(1)函数和是同一个函数吗?
(2)研究函数的基本性质.
(3)研究函数的基本性质,作出大致图像.
(4)联想祖暅原理,我们得到:“夹在两条平行线间的两个平面图形,被平行于这两条平行线的任意一条直线所截,如果截得的两条线段的长相等,那么这两个平面图形的面积相等。”请研究下列问题:设函数,请求出和与两条直线所围成的平面图形的面积。
提出问题
分析问题
解决问题
理性归纳
提出新问题……
1
第 4 页 共 9 页
一、教学目标
1、理解正切函数的定义及正切函数的图像特征,研究并掌握正切函数的基本性质。
2、在探究正切函数基本性质和图像的过程中,体验类比、数形结合等数学思想方法。
3、养成严谨的思维习惯,逐步提高逻辑推理、直观想象的核心素养。
二、教学重点 正切函数的图像与基本性质
三、教学难点 正切函数的最小正周期的理解 正切函数单调性的认识
四、核心知识 核心概念:正切函数的定义
核心方法:类比研究正切函数性质的思维方法
核心思想:研究函数性质中数形结合的思想方法
核心素养:逻辑推理、直观想象的核心素养
五、教学方法 探究体验、合作学习
六、教学流程图
教师:创设问题情境 启发探求思路 多元评价 理性概括
程序:
学生:接受问题挑战 自主探究 汇报交流 自主构建
七、教学过程
(一)、设置疑问,引入新课
1、正切函数的定义
对下列给出的正切函数的概念作比较,在比较中掌握正切函数的概念。
有同学,类比正弦函数、余弦函数的定义,定义了一个正切函数:
对于任意一个实数,都有唯一确定的值与它对应,按照这个对应法则所建立的函数,表示为,叫做正切函数.
大家认为这个定义是否完善? 强调:.
设计意图:,是学生容易出错的地方,通过学生之间的自我纠错,理解不能取的理由)。
今天我们就要研究正切函数()的图像与性质.
2、(前面)我们是怎样研究正弦函数的图像与性质的?
前面,我们在研究正弦函数的图像与性质是先作出正弦函数的图像,然后再由图像得到它的性质。今天,我们想改变一种研究的思路,即:先研究它的性质,然后在作它的图像。
(二)、主动探究,学习新知
1、利用定义,研究函数的性质 (学生自主研究探索正切函数的性质)
性质(1)定义域:.
性质(2)值域:R
说明:利用正切线得到正切函数的值域。
性质(3)奇偶性:奇函数.
说明:利用奇函数的定义得出结论。
性质(4)周期性:是最小正周期.
说明:学生会利用,得到是函数的周期后教师提问:能否说明是最小正周期? 引导学生思考能否利用周期函数的定义证明呢?(留作课后思考)
反证法:假设存在是的周期,
则都有.
取,则..,这与矛盾.从而,是正切函数的最小正周期.
我们已经知道了正切函数的一些基本性质,根据这些性质,你能勾画出正切函数的大致图像吗?
(三)结合性质,作出函数的图像
(1)自变量区间的选择。
说明:学生可能会作出下列的选择。
a、按周期选择、等;
b、按奇偶性选择。
根据学生的选择教师引导学生讨论,自变量区间的选择最好保证能够作出较为完整的图像,最后形成统一认识。
(2)利用计算器让学生感受正切函数的变化特点。
(3)借助于正切线,学生自主画出正切函数在上的图像。
(4)根据正切函数的周期性,把上述图像向左、右平移,得到正切函数
的图像.
(5)教师引导学生观察图象的特点,归纳出在要求不高的情况下作正切函数在上的简图画法:
三点;两线
(四)阅读课本,再议图像与性质
(1)观察图像,进一步理解性质。
思考下列问题,并说出理由。
1. 平行的虚线与正切函数的图像是否有交点?为什么?
2. 正切函数的单调性?你能从代数的角度去验证吗?
2. 正切函数的图像关于什么点对称?
(2)阅读课本,比较研究函数图像与性质的两个基本方法(先图后性质;先性质后图像)的特点。认识并掌握研究一个函数的图像与性质的两个基本方法。
思考下列问题,并说出理由。
(五)解决问题,巩固基础
例1.已知函数y=tanx,
(1)若,求y的取值范围;(2)若,求y的取值范围.
说明:
利用函数在区间上单调递增得到答案.
把y=tanx在区间上的图像不断向左、右扩展,也可得到正切函数的图像.因此, 有同学说正切函数在一个周期上递增是错误的.也可以对照说明,作正切函数图时选择的合理性.
例2.写出使不等式成立的x的集合.
说明:先求在上满足条件的,然后扩展到整个定义域.函数图像是函数的一种表达形式,形象地显示了函数的性质,为研究数量关系提供了“形”的直观性.它是探求解题途径,获得问题结果的重要工具,通过例题提醒学生重视数形结合的思想方法.
例3、研究函数的基本性质. 改为呢?
说明:大多数同学能够掌握的图像可以通过的图像向左平移个单位得到,从而方便地结合图像研究性质.
研究的性质要困难的多.希望同学能类比研究正弦、余弦函数时的方法解决,必要时通过代换来解决.
(六)总结思考,提高能力
学生交流在本节课学习中的体会、收获,交流学习过程中的体验和感受,师生合作共同完成小结.
(1) 理解了正切函数的定义;理解了正切函数的图像特征;掌握了正切函数的基本性质.
(2)运用了举反例、类比、反证法等数学方法,体会了数形结合的思想.
(七)分层作业,巩固拓展
1、全体同学完成课本95页第4、5题.
2、每位同学结合今天研究的内容,设计一道回家作业题,并选择下列问题中的1——2个问题进行研究。
(1)函数和是同一个函数吗?
(2)研究函数的基本性质.
(3)研究函数的基本性质,作出大致图像.
(4)联想祖暅原理,我们得到:“夹在两条平行线间的两个平面图形,被平行于这两条平行线的任意一条直线所截,如果截得的两条线段的长相等,那么这两个平面图形的面积相等。”请研究下列问题:设函数,请求出和与两条直线所围成的平面图形的面积。
附件一 《正切函数的图像与性质》学习任务工作单
一、学习任务
1、理解正切函数的定义及正切函数的图像特征,研究并掌握正切函数的基本性质。
2、在探究正切函数基本性质和图像的过程中,体验类比、数形结合等数学的思想方法。
3、养成严谨的思维习惯,逐步提高自己发现问题、提出问题、解决问题的能力。
二、任务学习
(一)概念学习:
正弦函数的概念:对于任意一个给定的实数 ,都有唯一确定的正弦值 sin 与之对应. 按
照这个对应关系所建立的函数叫做正弦函数,记作 =sin .
正切函数的概念
(二)正切函数的图像与性质的探究
序号 性质名称
1 定义域
2 值 域
3 最 值
4 奇偶性
5 周期性
6 单调性
7
8
(三)问题研究
例1.已知函数y=tanx,
(1)若,求y的取值范围;(2)若,求y的取值范围.
例2.写出使不等式成立的x的集合.
例3、研究函数的基本性质.
(四)小结交流 (思考今天的学习任务,将收获与同学交流。)
(五)拓展训练
1、完成课本95页第4、5题.
2、结合今天研究的内容,设计一道回家作业题,并选择下列问题中的1——2个问题进行研究。
(1)函数和是同一个函数吗?
(2)研究函数的基本性质.
(3)研究函数的基本性质,作出大致图像.
(4)联想祖暅原理,我们得到:“夹在两条平行线间的两个平面图形,被平行于这两条平行线的任意一条直线所截,如果截得的两条线段的长相等,那么这两个平面图形的面积相等。”请研究下列问题:设函数,请求出和与两条直线所围成的平面图形的面积。
提出问题
分析问题
解决问题
理性归纳
提出新问题……
1
第 4 页 共 9 页
