山东省英雄山中学2008-2009学年度高三年级质量检测数学试题(理科)
文档属性
| 名称 | 山东省英雄山中学2008-2009学年度高三年级质量检测数学试题(理科) |

|
|
| 格式 | rar | ||
| 文件大小 | 345.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-31 00:00:00 | ||
图片预览



文档简介
山东省英雄山中学2008—2009学年度高三年级质量检测
数学试题(理科)
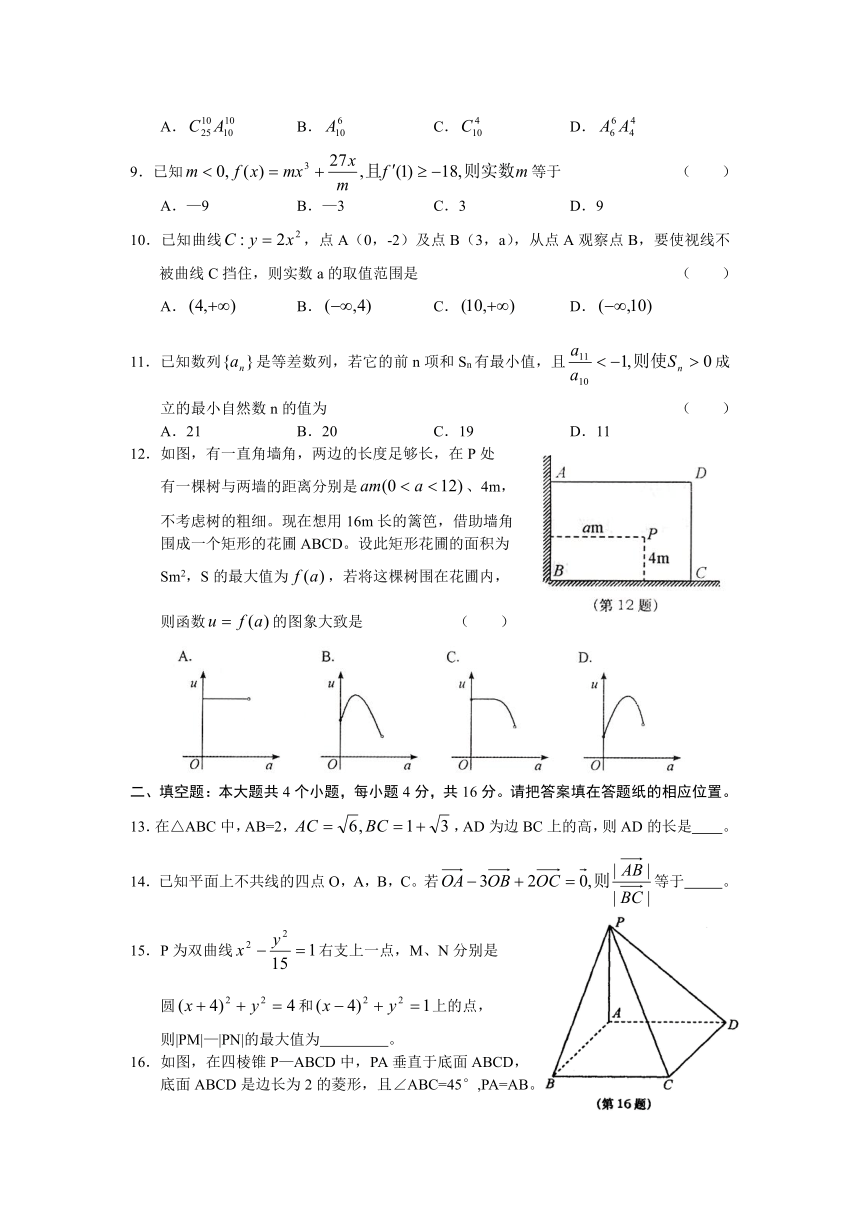
一、选择题:本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.化简= ( )
A. B. C. D.
2.设随机变量ξ服从标准正态分布N(0,1),在某项测量中,已知ξ在内取值的概率为0.025,则= ( )
A.0.025 B.0.050 C.0.950 D.0.975
3.已知命题p:“”,命题q:“”,若命题“p且q”是真命题,则实数a的取值范围是 ( )
A. B.
C. D.
4.右面程序运行后,输出的值是( )
A.42 B.43
C.44 D.45
5.设A、B、C、D是空间四个不同的点,
在下列命题中,不正确的是 ( )
A.若AC与BD共面,则AD与BC共面
B.若AC与BD是异面直线,则AD与BC是异面直线
C.若AB=AC,DB=DC,则AD⊥BC
D.若AB=AC,DB=DC,则AD=BC
6.若的值为 ( )
A. B. C. D.
7.已知实数x,y满足的最小值为—1,则实数m等于
( )
A.7 B.5 C.4 D.3
8.按分层抽样的方法,从15个相同的红球和10个相同的黑球中抽出10个球排成一排,则不同的排列方法为 ( )
A. B. C. D.
9.已知等于 ( )
A.—9 B.—3 C.3 D.9
10.已知曲线,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被曲线C挡住,则实数a的取值范围是 ( )
A. B. C. D.
11.已知数列是等差数列,若它的前n项和Sn有最小值,且成立的最小自然数n的值为 ( )
A.21 B.20 C.19 D.11
12.如图,有一直角墙角,两边的长度足够长,在P处
有一棵树与两墙的距离分别是、4m,
不考虑树的粗细。现在想用16m长的篱笆,借助墙角
围成一个矩形的花圃ABCD。设此矩形花圃的面积为
Sm2,S的最大值为,若将这棵树围在花圃内,
则函数的图象大致是 ( )
二、填空题:本大题共4个小题,每小题4分,共16分。请把答案填在答题纸的相应位置。
13.在△ABC中,AB=2,,AD为边BC上的高,则AD的长是 。
14.已知平面上不共线的四点O,A,B,C。若等于 。
15.P为双曲线右支上一点,M、N分别是
圆和上的点,
则|PM|—|PN|的最大值为 。
16.如图,在四棱锥P—ABCD中,PA垂直于底面ABCD,
底面ABCD是边长为2的菱形,且∠ABC=45°,PA=AB。
则直线AP与平面PBC所成的角的正切值是 。
三、解答题:本大题共6个小题,满分74分。解答应写出必要的文字说明、证明过程或演算步骤。请将解答过程写在答题纸的相应位置。
17.(本小题满分12分)
已知
(I)求函数的单调增区间;
(II)若的值。
18.(本小题满分12分)
已知数列上,其中n=1、2、3…。
(I)令是等比数列;
(II)求数列的通项。
19.(本小题满分12分)
袋中装有大致相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是;从袋中任意摸出2个球,至少得到1个白球的概率是
(I)求袋中各色球的个数;
(II)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
(III)若的值。
20.(本小题满分12分)
如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C
⊥平面ABCD,∠A1AC=60°。
(I)证明:BD⊥AA1;
(II)求二面角D-A1A-C的平面角的余弦值;
(III)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
(第20题)
21.(本小题满分12分)
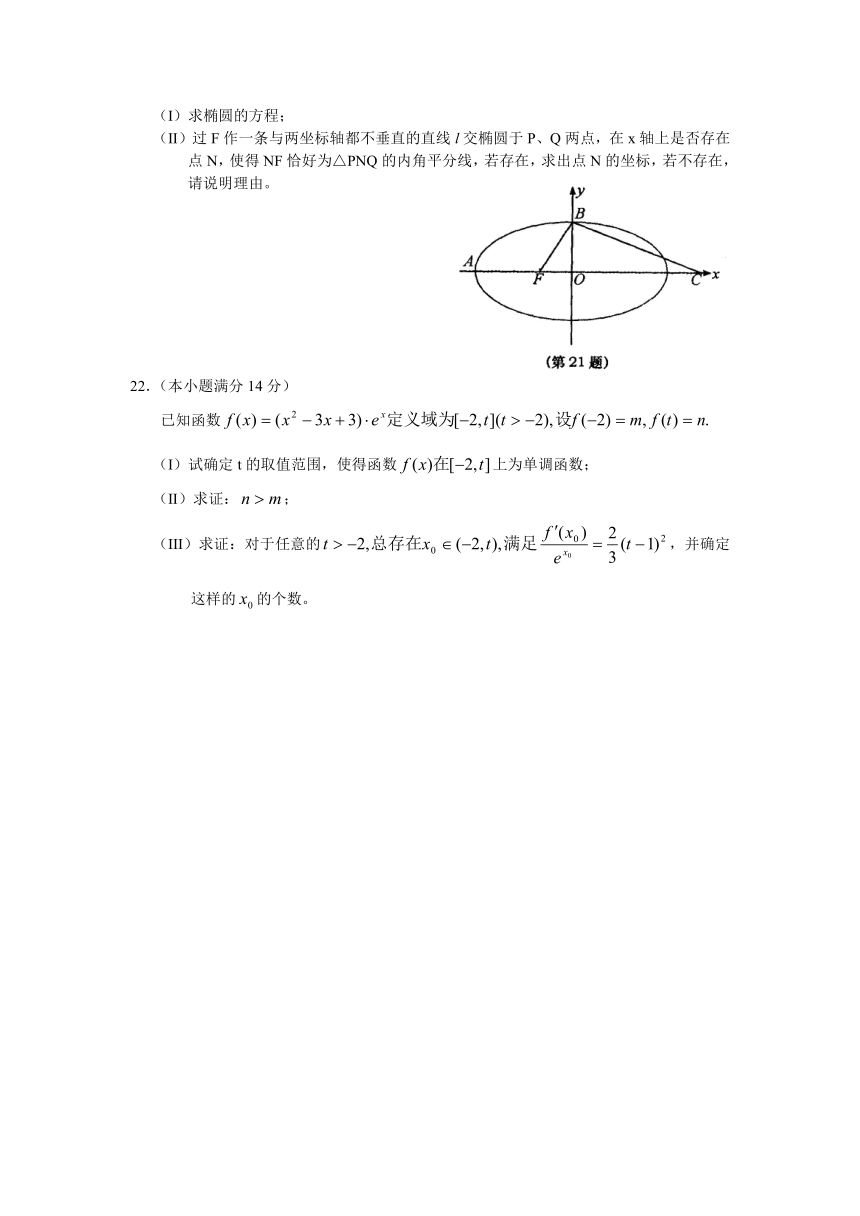
如图,F是椭圆的一个焦点,A、B是椭圆的两个顶点,椭圆的离心率为点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线相切。
(I)求椭圆的方程;
(II)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点,在x轴上是否存在点N,使得NF恰好为△PNQ的内角平分线,若存在,求出点N的坐标,若不存在,请说明理由。
22.(本小题满分14分)
已知函数
(I)试确定t的取值范围,使得函数上为单调函数;
(II)求证:;
(III)求证:对于任意的,并确定这样的的个数。
参考答案
一、选择题:本大题共12个小题,每小题5分,共60分。
1—5 DCACD 6—10 ABCBD 11—12 BC
二、填空题:本题共4个小题,每小题4分,共16分。
13. 14.2 15.5 16.
三、解答题:本题共6个小题,共74分。
17.(本小题满分12分)
解:(I)
(2)由(I)知,
………………12分
18.(本题满分12分)
解:(I) ………1分
(II)
19.(本小题满分12分)
解:(I)因为从袋中任意摸出1球得到黑球之概率是,故设黑球个数为x,则
………………1分
设白球的个数为y,又从袋中任意摸出2个球,至少得到1个白球的概率是,则
故袋中白球5个,黑球4个,红球1个。 ………………3分
(II)由题设知ξ的所有球取值是0,1,2,3,则随机变量ξ的分布列为
ξ 0 1 2 3
P
………………5分
(III)
20.(本小题满分12分)
解:连接BD交AC于O,则BD⊥AC,连接A1O
在△AA1O中,AA1=2,AO=1,∠A1AO=60°
∴A1O2=AA12+AO2-2AA1·AOcos60°=3
∴AO2+A1O2=A1A2
∴A1O⊥AO,由于平面AA1C1C⊥平面ABCD,
所以A1O⊥底面ABCD
∴以OB、OC、OA1所在直线为x轴、y轴、
z轴建立如图所示空间直角坐标系,
则A(0,-1,0),B(,0,0),C(0,1,0),D(-,0,0),A1(0,0,)
……………………2分
(Ⅰ)由于
则
∴BD⊥AA1……………………4分
(Ⅱ)由于OB⊥平面AA1C1C
∴平面AA1C1C的法向量
设⊥平面AA1D
则
得到……………………6分
所以二面角D—A1A—C的平面角的余弦值是……………………8分
(Ⅲ)假设在直线CC1上存在点P,使BP//平面DA1C1
设
则
得
……………………9分
设
则设
得到……………………10分
又因为平面DA1C1
则·
即点P在C1C的延长线上且使C1C=CP……………………12分
法二:在A1作A1O⊥AC于点O,由于平面AA1C 1C⊥平面
ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD
……………………4分
(Ⅱ)在△AA1O中,A1A=2,∠A1AO=60°
∴AO=AA1·cos60°=1
所以O是AC的中点,由于底面ABCD为菱形,所以
O也是BD中点
由(Ⅰ)可知DO⊥平面AA1C
过O作OE⊥AA1于E点,连接OE,则AA1⊥DE
则∠DEO为二面角D—AA1—C的平面角
……………………6分
在菱形ABCD中,AB=2,∠ABC=60°
∴AC=AB=BC=2
∴AO=1,DO=
在Rt△AEO中,OE=OA·sin∠EAO=
DE=
∴cos∠DEO=
∴二面角D—A1A—C的平面角的余弦值是……………………8分
(Ⅲ)存在这样的点P,连接B1C,因为A1B1ABDC
∴四边形A1B1CD为平行四边形。
∴A1D//B1C
在C1C的延长线上取点P,使C1C=CP,连接BP……………………10分
因B 1 BCC1,……………………12分
∴BB1CP
∴四边形BB1CP为平行四边形,则BP//B1C
∴BP//A1D
∴BP//平面DA1C1 ……………………12分
21.(本小题满分12分)
解:(I)由题意可知
(II)假设存在满足条件的点
由题意可设直线l的方程为
∴存在满足条件的点N,点N的坐标为(—4,0) ………………12分
22.(本小题满分14分)
解:(I)因为 …………1分
(II)证:因为处取得极小值e
(III)证:因为,
①当上有解,且只有一解
………………11分
②当,
所以上有解,且有两解
③当上有且只有一解;
y-c-y
数学试题(理科)
一、选择题:本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.化简= ( )
A. B. C. D.
2.设随机变量ξ服从标准正态分布N(0,1),在某项测量中,已知ξ在内取值的概率为0.025,则= ( )
A.0.025 B.0.050 C.0.950 D.0.975
3.已知命题p:“”,命题q:“”,若命题“p且q”是真命题,则实数a的取值范围是 ( )
A. B.
C. D.
4.右面程序运行后,输出的值是( )
A.42 B.43
C.44 D.45
5.设A、B、C、D是空间四个不同的点,
在下列命题中,不正确的是 ( )
A.若AC与BD共面,则AD与BC共面
B.若AC与BD是异面直线,则AD与BC是异面直线
C.若AB=AC,DB=DC,则AD⊥BC
D.若AB=AC,DB=DC,则AD=BC
6.若的值为 ( )
A. B. C. D.
7.已知实数x,y满足的最小值为—1,则实数m等于
( )
A.7 B.5 C.4 D.3
8.按分层抽样的方法,从15个相同的红球和10个相同的黑球中抽出10个球排成一排,则不同的排列方法为 ( )
A. B. C. D.
9.已知等于 ( )
A.—9 B.—3 C.3 D.9
10.已知曲线,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被曲线C挡住,则实数a的取值范围是 ( )
A. B. C. D.
11.已知数列是等差数列,若它的前n项和Sn有最小值,且成立的最小自然数n的值为 ( )
A.21 B.20 C.19 D.11
12.如图,有一直角墙角,两边的长度足够长,在P处
有一棵树与两墙的距离分别是、4m,
不考虑树的粗细。现在想用16m长的篱笆,借助墙角
围成一个矩形的花圃ABCD。设此矩形花圃的面积为
Sm2,S的最大值为,若将这棵树围在花圃内,
则函数的图象大致是 ( )
二、填空题:本大题共4个小题,每小题4分,共16分。请把答案填在答题纸的相应位置。
13.在△ABC中,AB=2,,AD为边BC上的高,则AD的长是 。
14.已知平面上不共线的四点O,A,B,C。若等于 。
15.P为双曲线右支上一点,M、N分别是
圆和上的点,
则|PM|—|PN|的最大值为 。
16.如图,在四棱锥P—ABCD中,PA垂直于底面ABCD,
底面ABCD是边长为2的菱形,且∠ABC=45°,PA=AB。
则直线AP与平面PBC所成的角的正切值是 。
三、解答题:本大题共6个小题,满分74分。解答应写出必要的文字说明、证明过程或演算步骤。请将解答过程写在答题纸的相应位置。
17.(本小题满分12分)
已知
(I)求函数的单调增区间;
(II)若的值。
18.(本小题满分12分)
已知数列上,其中n=1、2、3…。
(I)令是等比数列;
(II)求数列的通项。
19.(本小题满分12分)
袋中装有大致相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是;从袋中任意摸出2个球,至少得到1个白球的概率是
(I)求袋中各色球的个数;
(II)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
(III)若的值。
20.(本小题满分12分)
如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C
⊥平面ABCD,∠A1AC=60°。
(I)证明:BD⊥AA1;
(II)求二面角D-A1A-C的平面角的余弦值;
(III)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
(第20题)
21.(本小题满分12分)
如图,F是椭圆的一个焦点,A、B是椭圆的两个顶点,椭圆的离心率为点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线相切。
(I)求椭圆的方程;
(II)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点,在x轴上是否存在点N,使得NF恰好为△PNQ的内角平分线,若存在,求出点N的坐标,若不存在,请说明理由。
22.(本小题满分14分)
已知函数
(I)试确定t的取值范围,使得函数上为单调函数;
(II)求证:;
(III)求证:对于任意的,并确定这样的的个数。
参考答案
一、选择题:本大题共12个小题,每小题5分,共60分。
1—5 DCACD 6—10 ABCBD 11—12 BC
二、填空题:本题共4个小题,每小题4分,共16分。
13. 14.2 15.5 16.
三、解答题:本题共6个小题,共74分。
17.(本小题满分12分)
解:(I)
(2)由(I)知,
………………12分
18.(本题满分12分)
解:(I) ………1分
(II)
19.(本小题满分12分)
解:(I)因为从袋中任意摸出1球得到黑球之概率是,故设黑球个数为x,则
………………1分
设白球的个数为y,又从袋中任意摸出2个球,至少得到1个白球的概率是,则
故袋中白球5个,黑球4个,红球1个。 ………………3分
(II)由题设知ξ的所有球取值是0,1,2,3,则随机变量ξ的分布列为
ξ 0 1 2 3
P
………………5分
(III)
20.(本小题满分12分)
解:连接BD交AC于O,则BD⊥AC,连接A1O
在△AA1O中,AA1=2,AO=1,∠A1AO=60°
∴A1O2=AA12+AO2-2AA1·AOcos60°=3
∴AO2+A1O2=A1A2
∴A1O⊥AO,由于平面AA1C1C⊥平面ABCD,
所以A1O⊥底面ABCD
∴以OB、OC、OA1所在直线为x轴、y轴、
z轴建立如图所示空间直角坐标系,
则A(0,-1,0),B(,0,0),C(0,1,0),D(-,0,0),A1(0,0,)
……………………2分
(Ⅰ)由于
则
∴BD⊥AA1……………………4分
(Ⅱ)由于OB⊥平面AA1C1C
∴平面AA1C1C的法向量
设⊥平面AA1D
则
得到……………………6分
所以二面角D—A1A—C的平面角的余弦值是……………………8分
(Ⅲ)假设在直线CC1上存在点P,使BP//平面DA1C1
设
则
得
……………………9分
设
则设
得到……………………10分
又因为平面DA1C1
则·
即点P在C1C的延长线上且使C1C=CP……………………12分
法二:在A1作A1O⊥AC于点O,由于平面AA1C 1C⊥平面
ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD
……………………4分
(Ⅱ)在△AA1O中,A1A=2,∠A1AO=60°
∴AO=AA1·cos60°=1
所以O是AC的中点,由于底面ABCD为菱形,所以
O也是BD中点
由(Ⅰ)可知DO⊥平面AA1C
过O作OE⊥AA1于E点,连接OE,则AA1⊥DE
则∠DEO为二面角D—AA1—C的平面角
……………………6分
在菱形ABCD中,AB=2,∠ABC=60°
∴AC=AB=BC=2
∴AO=1,DO=
在Rt△AEO中,OE=OA·sin∠EAO=
DE=
∴cos∠DEO=
∴二面角D—A1A—C的平面角的余弦值是……………………8分
(Ⅲ)存在这样的点P,连接B1C,因为A1B1ABDC
∴四边形A1B1CD为平行四边形。
∴A1D//B1C
在C1C的延长线上取点P,使C1C=CP,连接BP……………………10分
因B 1 BCC1,……………………12分
∴BB1CP
∴四边形BB1CP为平行四边形,则BP//B1C
∴BP//A1D
∴BP//平面DA1C1 ……………………12分
21.(本小题满分12分)
解:(I)由题意可知
(II)假设存在满足条件的点
由题意可设直线l的方程为
∴存在满足条件的点N,点N的坐标为(—4,0) ………………12分
22.(本小题满分14分)
解:(I)因为 …………1分
(II)证:因为处取得极小值e
(III)证:因为,
①当上有解,且只有一解
………………11分
②当,
所以上有解,且有两解
③当上有且只有一解;
y-c-y
同课章节目录
