六年级下册数学人教版小升初专题复习——比和比例的认识课件(共20张PPT)
文档属性
| 名称 | 六年级下册数学人教版小升初专题复习——比和比例的认识课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 597.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
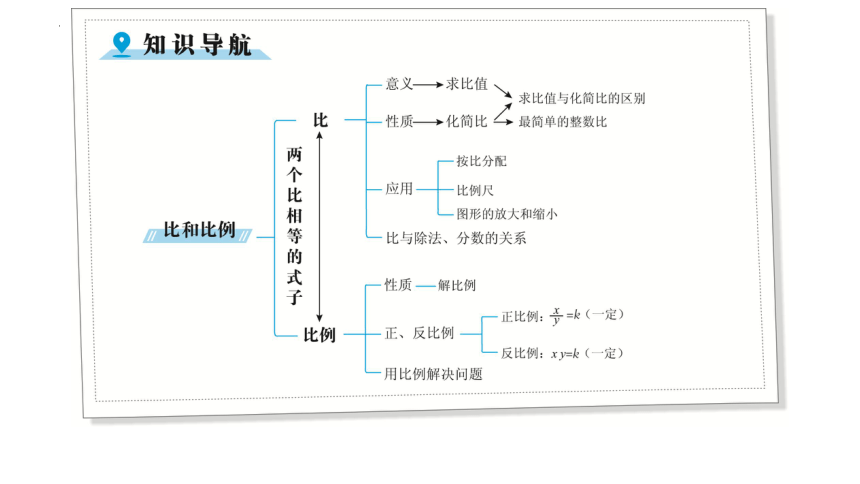
比和比例的认识
比的意义和基本性质
1.比的意义:两个数相除又叫作两个数的比。
2.比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比
值不变。
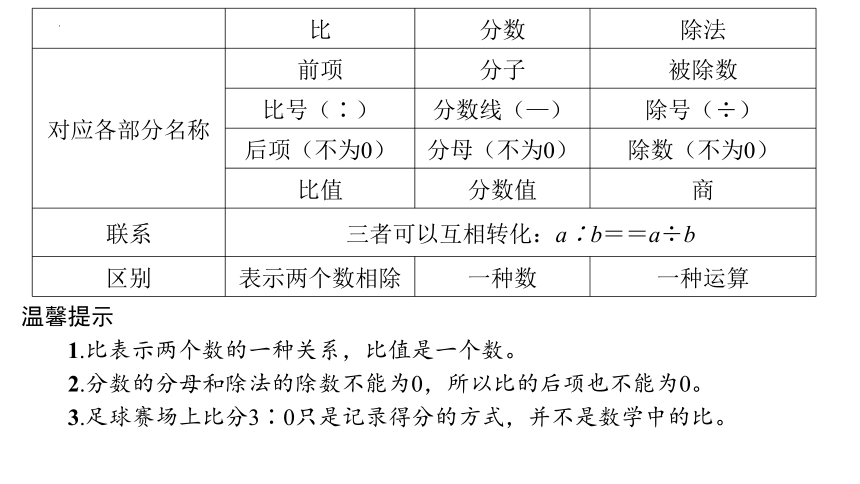
3.比和除法、分数的区别和联系
比 分数 除法
对应各部分名称 前项 分子 被除数
比号(∶) 分数线(—) 除号(÷)
后项(不为0) 分母(不为0) 除数(不为0)
比值 分数值 商
联系 三者可以互相转化:a∶b==a÷b
区别 表示两个数相除 一种数 一种运算
温馨提示
1.比表示两个数的一种关系,比值是一个数。
2.分数的分母和除法的除数不能为0,所以比的后项也不能为0。
3.足球赛场上比分3∶0只是记录得分的方式,并不是数学中的比。
求比值和化简比
意义 方法或依据 结果
求比值 前项除以后项的商 前项除以后项 一个数
化简比 把原比化成最简单的整数比
(前项和后项互质) 比的基本性质 一个比
温馨提示
对带单位的两个同类量的比进行化简时,先统一单位,再化简。化简比
的结果必须是比,即使后项是1也不能省略。
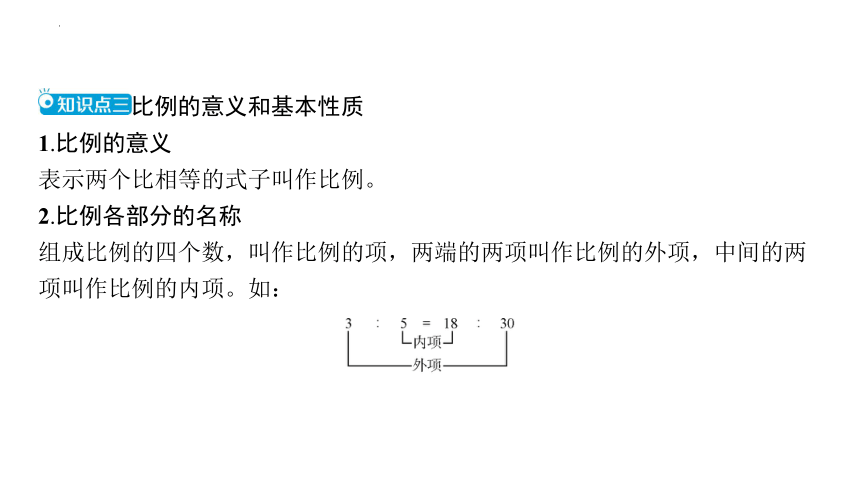
比例的意义和基本性质
1.比例的意义
表示两个比相等的式子叫作比例。
2.比例各部分的名称
组成比例的四个数,叫作比例的项,两端的两项叫作比例的外项,中间的两
项叫作比例的内项。如:
3.比例的基本性质
在一个比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
温馨提示
判断两个比能否组成比例,一般是看两个比的比值是否相等;还可以根
据比例的基本性质,看所给出的四个数,其中两个数的积与另外两个数的积
是否相等,如果相等就可以组成比例。但要注意,组成比例的四个项都不能
为0。
解比例
1.解比例就是求比例中的未知项的过程。
2.解比例的根据是比例的基本性质。
3.解比例的步骤和方法。
解比例时,先根据比例的基本性质把原比例a∶b=c∶d改写成一般方程ad=
bc的形式,再求该方程的解。
温馨提示
解比例的小窍门:
(1)一化:把比例转化为一般方程。
(2)二解:求方程的解。
正比例和反比例
正比例关系 反比例关系
相同点 两种相关联的量,一种量变化,另一种量也随着变化
不同点 两种量相对应的两个
数,比值一定 两种量中相对应的两个数的乘积一定
关系式 =k(一定) xy=k(一定)
巧记
1.当速度一定时,路程和时间成正比例。
2.当长方形的面积一定时,长和宽成反比例。
典例1
(1)圆的周长和直径的比值是( )。
(2)4∶9的前项乘3,要使比值不变,后项应加( )。
(1)圆的周长C=πd,那么圆的周长和直径的比值是πd∶d=π。
(2)比的前项乘3,要使比值不变,根据比的基本性质,后项也要乘3,9×3
=27,后项要加27-9=18。
(1)π (2)18
即时训练1:a与b的商是,a与b的比是( 5∶8 )。
5∶8
典例2
化简比并求比值:∶。
将比的前项和后项同时乘它们的分母的最小公倍数变成整数比,再化
简。
∶=(×9)∶(×9)=8∶6=4∶3 比值为
即时训练2:化简比并求比值。
(1)0.8∶1.6
【答案】1∶2 比值为
(2)∶
【答案】20∶3 比值为
典例3
已知5a=4b(a,b均不为0),那么a∶b=( )∶( )。
根据比例的基本性质,两个内项的积等于两个外项的积来形成比例。
写出比例后,再利用比例基本性质检验是否符合条件。
4∶5
即时训练 3:24的因数有( 1,24,2,12,3,8,4,6 ),选出其中的4
个组成比例是( 4∶2=12∶6(答案不唯一) )。
即时训练 4:甲、乙均不为0,如果甲的等于乙的,那么甲∶乙=
( 9∶8 )。
1,24,2,12,3,8,4,6
4∶2=12∶6(答案不唯一)
9∶8
典例4
解比例:=。
根据比例的基本性质,先转化成3(x+1)=2.25×4,再用解方程的
方法求出未知项。
x=2
即时训练5:解比例。
(1)∶18%=
(2)=
【答案】x=15.6
【答案】x=18
一、填空。
1.12÷20=( 3 )∶5==( 60 )%。
2.大、小两圆的半径比是2∶1,则大、小两圆的直径比是( 2 )∶( 1 ),
周长比是( 2 )∶( 1 ),面积比是( 4 )∶( 1 )。
3.∶9的比值是( ),如果前项加上1.2,要使比值不变,后项应增加
( 18 )。
4.甲∶乙=4∶3,乙∶丙=4∶9,则甲∶乙∶丙=( 16∶12∶27 )。
3
60
2
1
2
1
4
1
18
16∶12∶27
5.在A×B=C中(A,B,C都不为0),当B一定时,A和C成( 正 )比
例;当C一定时,A和B成( 反 )比例。
6.=,那么x∶y=( (或4∶9) ),如果x=1.2,则y=( 2.7 )。
7.在12,8,16这三个数中添上一个数组成比例,这个数可以是( 6 ),
( 24 )或( )。
正
反
(或4∶9)
2.7
6
24
二、选择。
1.下面两个比不.能.组成比例的是( B )。
A.10∶12和35∶42 B.20∶10和60∶20
C.∶和12∶8 D.0.6∶0.2和∶
2.下列各项中两种量成反比例关系的是( B )。
A.长方形的周长一定,长和宽
B.铺地面积一定,每块砖的面积和用砖块数
C.一瓶油的总量一定,用去的和剩下的
D.汽车车轮周长一定,车轮行驶的路程和转数
B
B
3.一堆沙分两次运完,第一次运走了总量的,第二次运走了吨,第一次和第
二次运的吨数比( C )。
A.1∶1 B.3∶4 C.4∶3 D.7∶3
4.一个长方形的周长是30分米,长和宽的比是3∶2,下列说法错误的是
( B )。
A.宽是长的 B.宽和周长的比是2∶5
C.长9分米 D.面积54平方分米
C
B
三、化简下列各比,并求出比值。
(1)0.7∶0.8
【答案】7∶8
(2)1.2∶
【答案】36∶25
(3)时∶30分
【答案】4∶5
(4)450千克∶5.5吨
【答案】9∶110
四、解比例。
(1)∶18=∶x
【答案】x=54
(2)0.9∶0.6=
【答案】x=4.05
(3)0.6∶x=∶0.25
【答案】x=
(4)=∶
【答案】x=
五、解决问题。
如图,一个平行四边形被两条直线分成4个小平行四边形,其中三个的面积分
别是22cm2,33cm2,90cm2。阴影部分的面积是多少?
【答案】设阴影部分的面积是xcm2。
33∶22=90∶x,x=60
比和比例的认识
比的意义和基本性质
1.比的意义:两个数相除又叫作两个数的比。
2.比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比
值不变。
3.比和除法、分数的区别和联系
比 分数 除法
对应各部分名称 前项 分子 被除数
比号(∶) 分数线(—) 除号(÷)
后项(不为0) 分母(不为0) 除数(不为0)
比值 分数值 商
联系 三者可以互相转化:a∶b==a÷b
区别 表示两个数相除 一种数 一种运算
温馨提示
1.比表示两个数的一种关系,比值是一个数。
2.分数的分母和除法的除数不能为0,所以比的后项也不能为0。
3.足球赛场上比分3∶0只是记录得分的方式,并不是数学中的比。
求比值和化简比
意义 方法或依据 结果
求比值 前项除以后项的商 前项除以后项 一个数
化简比 把原比化成最简单的整数比
(前项和后项互质) 比的基本性质 一个比
温馨提示
对带单位的两个同类量的比进行化简时,先统一单位,再化简。化简比
的结果必须是比,即使后项是1也不能省略。
比例的意义和基本性质
1.比例的意义
表示两个比相等的式子叫作比例。
2.比例各部分的名称
组成比例的四个数,叫作比例的项,两端的两项叫作比例的外项,中间的两
项叫作比例的内项。如:
3.比例的基本性质
在一个比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
温馨提示
判断两个比能否组成比例,一般是看两个比的比值是否相等;还可以根
据比例的基本性质,看所给出的四个数,其中两个数的积与另外两个数的积
是否相等,如果相等就可以组成比例。但要注意,组成比例的四个项都不能
为0。
解比例
1.解比例就是求比例中的未知项的过程。
2.解比例的根据是比例的基本性质。
3.解比例的步骤和方法。
解比例时,先根据比例的基本性质把原比例a∶b=c∶d改写成一般方程ad=
bc的形式,再求该方程的解。
温馨提示
解比例的小窍门:
(1)一化:把比例转化为一般方程。
(2)二解:求方程的解。
正比例和反比例
正比例关系 反比例关系
相同点 两种相关联的量,一种量变化,另一种量也随着变化
不同点 两种量相对应的两个
数,比值一定 两种量中相对应的两个数的乘积一定
关系式 =k(一定) xy=k(一定)
巧记
1.当速度一定时,路程和时间成正比例。
2.当长方形的面积一定时,长和宽成反比例。
典例1
(1)圆的周长和直径的比值是( )。
(2)4∶9的前项乘3,要使比值不变,后项应加( )。
(1)圆的周长C=πd,那么圆的周长和直径的比值是πd∶d=π。
(2)比的前项乘3,要使比值不变,根据比的基本性质,后项也要乘3,9×3
=27,后项要加27-9=18。
(1)π (2)18
即时训练1:a与b的商是,a与b的比是( 5∶8 )。
5∶8
典例2
化简比并求比值:∶。
将比的前项和后项同时乘它们的分母的最小公倍数变成整数比,再化
简。
∶=(×9)∶(×9)=8∶6=4∶3 比值为
即时训练2:化简比并求比值。
(1)0.8∶1.6
【答案】1∶2 比值为
(2)∶
【答案】20∶3 比值为
典例3
已知5a=4b(a,b均不为0),那么a∶b=( )∶( )。
根据比例的基本性质,两个内项的积等于两个外项的积来形成比例。
写出比例后,再利用比例基本性质检验是否符合条件。
4∶5
即时训练 3:24的因数有( 1,24,2,12,3,8,4,6 ),选出其中的4
个组成比例是( 4∶2=12∶6(答案不唯一) )。
即时训练 4:甲、乙均不为0,如果甲的等于乙的,那么甲∶乙=
( 9∶8 )。
1,24,2,12,3,8,4,6
4∶2=12∶6(答案不唯一)
9∶8
典例4
解比例:=。
根据比例的基本性质,先转化成3(x+1)=2.25×4,再用解方程的
方法求出未知项。
x=2
即时训练5:解比例。
(1)∶18%=
(2)=
【答案】x=15.6
【答案】x=18
一、填空。
1.12÷20=( 3 )∶5==( 60 )%。
2.大、小两圆的半径比是2∶1,则大、小两圆的直径比是( 2 )∶( 1 ),
周长比是( 2 )∶( 1 ),面积比是( 4 )∶( 1 )。
3.∶9的比值是( ),如果前项加上1.2,要使比值不变,后项应增加
( 18 )。
4.甲∶乙=4∶3,乙∶丙=4∶9,则甲∶乙∶丙=( 16∶12∶27 )。
3
60
2
1
2
1
4
1
18
16∶12∶27
5.在A×B=C中(A,B,C都不为0),当B一定时,A和C成( 正 )比
例;当C一定时,A和B成( 反 )比例。
6.=,那么x∶y=( (或4∶9) ),如果x=1.2,则y=( 2.7 )。
7.在12,8,16这三个数中添上一个数组成比例,这个数可以是( 6 ),
( 24 )或( )。
正
反
(或4∶9)
2.7
6
24
二、选择。
1.下面两个比不.能.组成比例的是( B )。
A.10∶12和35∶42 B.20∶10和60∶20
C.∶和12∶8 D.0.6∶0.2和∶
2.下列各项中两种量成反比例关系的是( B )。
A.长方形的周长一定,长和宽
B.铺地面积一定,每块砖的面积和用砖块数
C.一瓶油的总量一定,用去的和剩下的
D.汽车车轮周长一定,车轮行驶的路程和转数
B
B
3.一堆沙分两次运完,第一次运走了总量的,第二次运走了吨,第一次和第
二次运的吨数比( C )。
A.1∶1 B.3∶4 C.4∶3 D.7∶3
4.一个长方形的周长是30分米,长和宽的比是3∶2,下列说法错误的是
( B )。
A.宽是长的 B.宽和周长的比是2∶5
C.长9分米 D.面积54平方分米
C
B
三、化简下列各比,并求出比值。
(1)0.7∶0.8
【答案】7∶8
(2)1.2∶
【答案】36∶25
(3)时∶30分
【答案】4∶5
(4)450千克∶5.5吨
【答案】9∶110
四、解比例。
(1)∶18=∶x
【答案】x=54
(2)0.9∶0.6=
【答案】x=4.05
(3)0.6∶x=∶0.25
【答案】x=
(4)=∶
【答案】x=
五、解决问题。
如图,一个平行四边形被两条直线分成4个小平行四边形,其中三个的面积分
别是22cm2,33cm2,90cm2。阴影部分的面积是多少?
【答案】设阴影部分的面积是xcm2。
33∶22=90∶x,x=60
同课章节目录
