六年级下册数学人教版小升初专题复习---整数、小数实际问题(课件)(共12张PPT)
文档属性
| 名称 | 六年级下册数学人教版小升初专题复习---整数、小数实际问题(课件)(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 163.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 14:57:35 | ||
图片预览




文档简介
(共12张PPT)
整数、小数实际问题
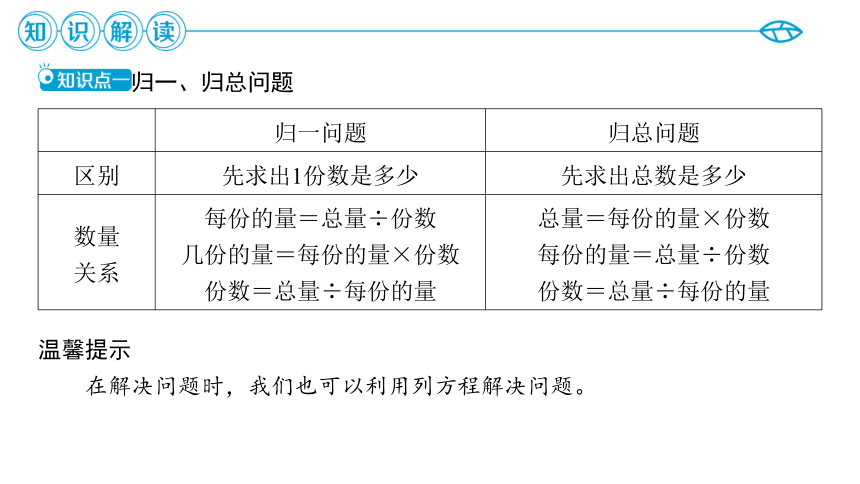
归一、归总问题
归一问题 归总问题
区别 先求出1份数是多少 先求出总数是多少
数量 关系 每份的量=总量÷份数 几份的量=每份的量×份数 份数=总量÷每份的量 总量=每份的量×份数
每份的量=总量÷份数
份数=总量÷每份的量
温馨提示
在解决问题时,我们也可以利用列方程解决问题。
行程问题
相遇问题 追及问题
数量 关系 总路程=速度和×相遇时间 相遇时间=总路程÷速度和 速度和=总路程÷相遇时间 追及时间=路程差÷速度差
速度差=路程差÷追及时间
路程差=速度差×追及时间
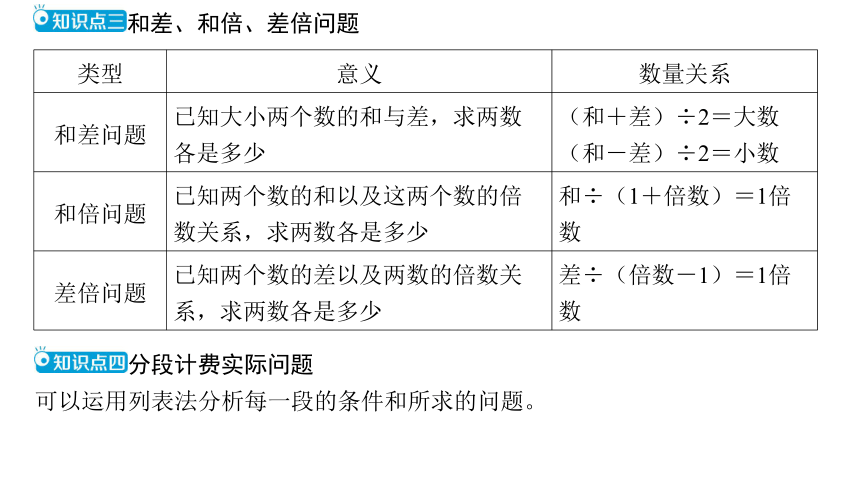
和差、和倍、差倍问题
类型 意义 数量关系
和差问题 已知大小两个数的和与差,求两数
各是多少 (和+差)÷2=大数
(和-差)÷2=小数
和倍问题 已知两个数的和以及这两个数的倍
数关系,求两数各是多少 和÷(1+倍数)=1倍
数
差倍问题 已知两个数的差以及两数的倍数关
系,求两数各是多少 差÷(倍数-1)=1倍
数
分段计费实际问题
可以运用列表法分析每一段的条件和所求的问题。
典例1
光明小学购入一批纸,计划每天用20张,可以用28天。为了响应节约用纸
的号召,实际每天只用了16张。这批纸实际比计划多用多少天?
本题是一道“归总和归一”的实际问题,先求出白纸的总数量,再根
据总量求出实际的天数。
20×28÷16-28=7(天)
即时训练1:学校新购了4张同样的电脑桌和3把同样的椅子,共用去1480元。
已知每张电脑桌280元,每把椅子多少钱?
【答案】(1480-280×4)÷3=120(元)
典例2
一辆汽车以每小时75千米的速度从甲地开往乙地,行驶了3.5小时,距离中
点还有20千米。甲、乙两地相距多少千米?
根据“路程=速度×时间”,计算出汽车行驶路程,再根据“距中点
还有20千米”,计算出甲、乙两地的距离。
(75×3.5+20)×2=565(千米)
即时训练2:王军和李明在400米长的环形跑道步行。王军每分钟行120米,李
明每分钟行80米。两人同一地点,同时出发,同向而行多少分钟后,两人第
一次相遇?
【答案】400÷(120-80)=10(分钟)
典例3
学校阅览室购进科技书的本书是故事书的2.5倍,购进的科技书比故事书多
420本。购进科技书和故事书各多少本?
假设故事书的本数是1份,则科技书的本数就是2.5份,420本对应的份
数是(2.5-1)。
故事书:420÷(2.5-1)=280(本) 科技书:280×2.5=700(本)
即时训练3:甲、乙两车同时从相距810千米的两地相对开出,经过6小时两车
相遇。已知乙车速度是甲车速度的1.25倍,甲车每小时行多少千米?
【答案】(810÷6)÷(1+1.25)=60(千米)
典例4
某市出租车的收费标准如下:
里程 收费
起步价:3km以内(含3km) 8.00元
3km以上,每超过1km(不足1km按1km计算) 2.60元
(1)请你算一算,一次性乘车7.3km,需要付多少元?
(2)如果你有47元钱,最多可以乘车多少千米?
本题考察分段计费的问题。根据题意把费用分成两段分别计算。
(1)7.3km≈8km 8+(8-3)×2.6=21(元) (2)(47-8)
÷2.6+3=18(km)
即时训练4:某市用水收费标准如下:每户每月的用水量不超过20m3时,水费
按“基本价”收费;超过20m3时,不超过的部分仍按“基本价”收费,超过
部分按“调节价”收费。
月份 用水量/m3 水费/元
四 18 41.40
五 26 66.40
(1)王老师家这两个月用水情况如下表,该市水费的“基本价”和“调节
价”每立方米各是多少元?
【答案】“基本价”每立方米:41.40÷18=2.3(元)
“调节价”每立方米:(66.40-2.3×20)÷(26-20)=3.4(元)
(2)若王老师家六月份的用水量为35m3,则六月份的水费是多少元?
【答案】2.3×20+(35-20)×3.4=97(元)
一、填空。
1.哥哥和弟弟今年年龄之和是47岁,5年后,哥哥比弟弟大5岁,哥哥今年
( 26 )岁,弟弟今年( 21 )岁。
2.一个数的小数点向左移动一位,结果比原来少34.65,这个数原来是
( 38.5 )。
3.方方收集了一些邮票,他拿出自己邮票的一半还多2枚送给齐齐,自己还剩
40枚,方方原来有( 84 )枚邮票。
4.小丽在做一道减法算式时,把减数个位的1看成了7,把减数十位上的7看成
了1,结果差是111,正确答案应该是( 57 )。
26
21
38.5
84
57
5.小红家有一桶油,连桶重8kg,用去一半后连桶重4.5kg。原来桶内油重
( 7 )kg,油桶重( 1 )kg。
6.在一条长560m的公路两侧种树,每隔8m种一棵,两端都要种,一共种
( 142 )棵。
7
1
142
二、解决问题。
1.一台笔记本电脑的价格是7800元,比一台彩电价格的3倍少1500元。这台彩
电的价格是多少元?
【答案】(7800+1500)÷3=3100(元)
2.有两根同样长的绳子,第一根截去12米,第二根接上14米,这时第二根长
度是第一根的3倍。这两根绳子原来长多少米?
【答案】(12+14)÷(3-1)=13(米) 13+12=25(米)
3.五(3)班同学排队做操,如果每排5人多出2人,如果每排6人,还是多出2
人。已知五(3)班的人数在30~50之间。五(3)班有多少名同学?
【答案】5和6的最小公倍是30。30+2=32(人)
4.一辆客车和一辆轿车先后从杭州出发去上海,客车先行50km后,轿车出
发,客车平均每小时行80km,轿车平均每小时行100km。轿车几小时后追上
客车?
【答案】50÷(100-80)=2.5(小时)
5.某市推行阶梯水价,居民生活用水基本水价为1.8元/立方米,月用水量不超
过25立方米,按基本水价收费;超过25立方米部分按2.4元/立方米收费。
(1)王明家5月用水27立方米,应缴水费多少元?
【答案】25×1.8+(27-25)×2.4=49.8(元)
(2)李俊家5月缴水费66.6元,他家该月用水多少立方米?
【答案】(66.6-25×1.8)÷2.4+25=34(立方米)
整数、小数实际问题
归一、归总问题
归一问题 归总问题
区别 先求出1份数是多少 先求出总数是多少
数量 关系 每份的量=总量÷份数 几份的量=每份的量×份数 份数=总量÷每份的量 总量=每份的量×份数
每份的量=总量÷份数
份数=总量÷每份的量
温馨提示
在解决问题时,我们也可以利用列方程解决问题。
行程问题
相遇问题 追及问题
数量 关系 总路程=速度和×相遇时间 相遇时间=总路程÷速度和 速度和=总路程÷相遇时间 追及时间=路程差÷速度差
速度差=路程差÷追及时间
路程差=速度差×追及时间
和差、和倍、差倍问题
类型 意义 数量关系
和差问题 已知大小两个数的和与差,求两数
各是多少 (和+差)÷2=大数
(和-差)÷2=小数
和倍问题 已知两个数的和以及这两个数的倍
数关系,求两数各是多少 和÷(1+倍数)=1倍
数
差倍问题 已知两个数的差以及两数的倍数关
系,求两数各是多少 差÷(倍数-1)=1倍
数
分段计费实际问题
可以运用列表法分析每一段的条件和所求的问题。
典例1
光明小学购入一批纸,计划每天用20张,可以用28天。为了响应节约用纸
的号召,实际每天只用了16张。这批纸实际比计划多用多少天?
本题是一道“归总和归一”的实际问题,先求出白纸的总数量,再根
据总量求出实际的天数。
20×28÷16-28=7(天)
即时训练1:学校新购了4张同样的电脑桌和3把同样的椅子,共用去1480元。
已知每张电脑桌280元,每把椅子多少钱?
【答案】(1480-280×4)÷3=120(元)
典例2
一辆汽车以每小时75千米的速度从甲地开往乙地,行驶了3.5小时,距离中
点还有20千米。甲、乙两地相距多少千米?
根据“路程=速度×时间”,计算出汽车行驶路程,再根据“距中点
还有20千米”,计算出甲、乙两地的距离。
(75×3.5+20)×2=565(千米)
即时训练2:王军和李明在400米长的环形跑道步行。王军每分钟行120米,李
明每分钟行80米。两人同一地点,同时出发,同向而行多少分钟后,两人第
一次相遇?
【答案】400÷(120-80)=10(分钟)
典例3
学校阅览室购进科技书的本书是故事书的2.5倍,购进的科技书比故事书多
420本。购进科技书和故事书各多少本?
假设故事书的本数是1份,则科技书的本数就是2.5份,420本对应的份
数是(2.5-1)。
故事书:420÷(2.5-1)=280(本) 科技书:280×2.5=700(本)
即时训练3:甲、乙两车同时从相距810千米的两地相对开出,经过6小时两车
相遇。已知乙车速度是甲车速度的1.25倍,甲车每小时行多少千米?
【答案】(810÷6)÷(1+1.25)=60(千米)
典例4
某市出租车的收费标准如下:
里程 收费
起步价:3km以内(含3km) 8.00元
3km以上,每超过1km(不足1km按1km计算) 2.60元
(1)请你算一算,一次性乘车7.3km,需要付多少元?
(2)如果你有47元钱,最多可以乘车多少千米?
本题考察分段计费的问题。根据题意把费用分成两段分别计算。
(1)7.3km≈8km 8+(8-3)×2.6=21(元) (2)(47-8)
÷2.6+3=18(km)
即时训练4:某市用水收费标准如下:每户每月的用水量不超过20m3时,水费
按“基本价”收费;超过20m3时,不超过的部分仍按“基本价”收费,超过
部分按“调节价”收费。
月份 用水量/m3 水费/元
四 18 41.40
五 26 66.40
(1)王老师家这两个月用水情况如下表,该市水费的“基本价”和“调节
价”每立方米各是多少元?
【答案】“基本价”每立方米:41.40÷18=2.3(元)
“调节价”每立方米:(66.40-2.3×20)÷(26-20)=3.4(元)
(2)若王老师家六月份的用水量为35m3,则六月份的水费是多少元?
【答案】2.3×20+(35-20)×3.4=97(元)
一、填空。
1.哥哥和弟弟今年年龄之和是47岁,5年后,哥哥比弟弟大5岁,哥哥今年
( 26 )岁,弟弟今年( 21 )岁。
2.一个数的小数点向左移动一位,结果比原来少34.65,这个数原来是
( 38.5 )。
3.方方收集了一些邮票,他拿出自己邮票的一半还多2枚送给齐齐,自己还剩
40枚,方方原来有( 84 )枚邮票。
4.小丽在做一道减法算式时,把减数个位的1看成了7,把减数十位上的7看成
了1,结果差是111,正确答案应该是( 57 )。
26
21
38.5
84
57
5.小红家有一桶油,连桶重8kg,用去一半后连桶重4.5kg。原来桶内油重
( 7 )kg,油桶重( 1 )kg。
6.在一条长560m的公路两侧种树,每隔8m种一棵,两端都要种,一共种
( 142 )棵。
7
1
142
二、解决问题。
1.一台笔记本电脑的价格是7800元,比一台彩电价格的3倍少1500元。这台彩
电的价格是多少元?
【答案】(7800+1500)÷3=3100(元)
2.有两根同样长的绳子,第一根截去12米,第二根接上14米,这时第二根长
度是第一根的3倍。这两根绳子原来长多少米?
【答案】(12+14)÷(3-1)=13(米) 13+12=25(米)
3.五(3)班同学排队做操,如果每排5人多出2人,如果每排6人,还是多出2
人。已知五(3)班的人数在30~50之间。五(3)班有多少名同学?
【答案】5和6的最小公倍是30。30+2=32(人)
4.一辆客车和一辆轿车先后从杭州出发去上海,客车先行50km后,轿车出
发,客车平均每小时行80km,轿车平均每小时行100km。轿车几小时后追上
客车?
【答案】50÷(100-80)=2.5(小时)
5.某市推行阶梯水价,居民生活用水基本水价为1.8元/立方米,月用水量不超
过25立方米,按基本水价收费;超过25立方米部分按2.4元/立方米收费。
(1)王明家5月用水27立方米,应缴水费多少元?
【答案】25×1.8+(27-25)×2.4=49.8(元)
(2)李俊家5月缴水费66.6元,他家该月用水多少立方米?
【答案】(66.6-25×1.8)÷2.4+25=34(立方米)
同课章节目录
