六年级下册数学人教版小升初专题复习---四则运算的意义和法则课件(共22张PPT)
文档属性
| 名称 | 六年级下册数学人教版小升初专题复习---四则运算的意义和法则课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 792.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览





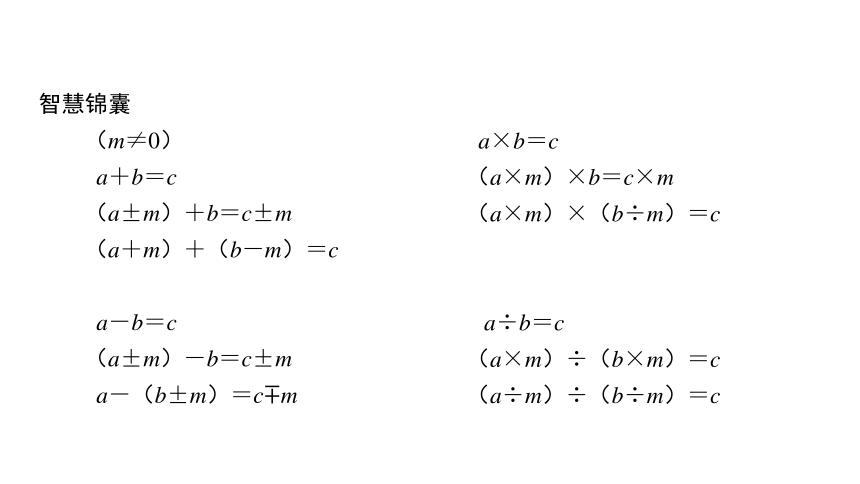
文档简介
(共22张PPT)
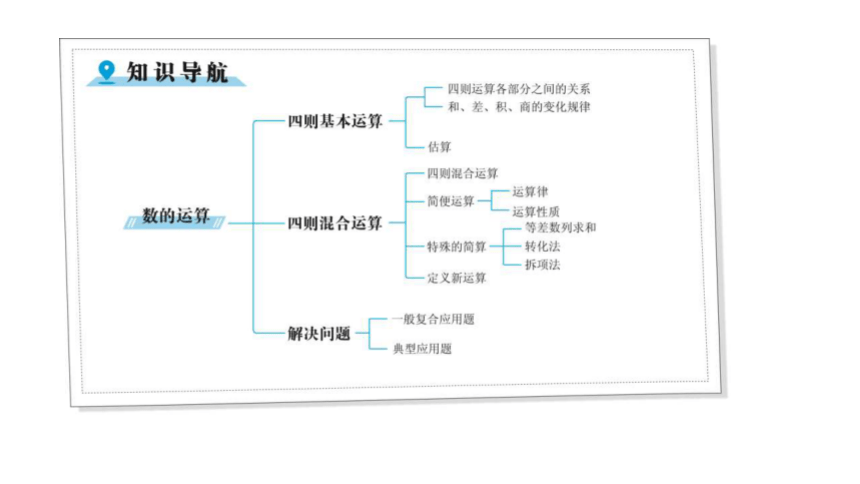
四则运算的意义和法则
四则运算的意义、法则
1.四则运算的意义
运算名称 相关概念与意义
加法 把两个数合并成一个数的运算
相加的数叫作加数,相加的结果叫作和
减法 已知两个加数的和与其中一个加数,求另一个加数的运算
乘法 求几个相同加数和的简便运算。相乘的两数叫因数,相乘的结果
叫积
除法 已知两个因数的积与其中一个因数,求另一个因数的运算
温馨提示
四则运算是“加、减、乘、除”四种运算的统称。
减法是加法的逆运算。
除法是乘法的逆运算。
2.四则运算的法则
(1)加、减法的法则
整数 小数 分数
①相同数位对齐 ②从低位算起 ③加法中满十就向
前一位进一;减法
中不够减时,就从
前一位借一当十 ①相同数位对齐(小数点对
齐) ②从低位算起 ③按整数加、减法的法则进行
计算 ④结果中的小数点和相加、减
的数里的小数点对齐 ①同分母分数相加减,
分母不变,分子相加减
②异分母分数相加减,
先通分然后计算
③结果能约分的要约分
成最简分数
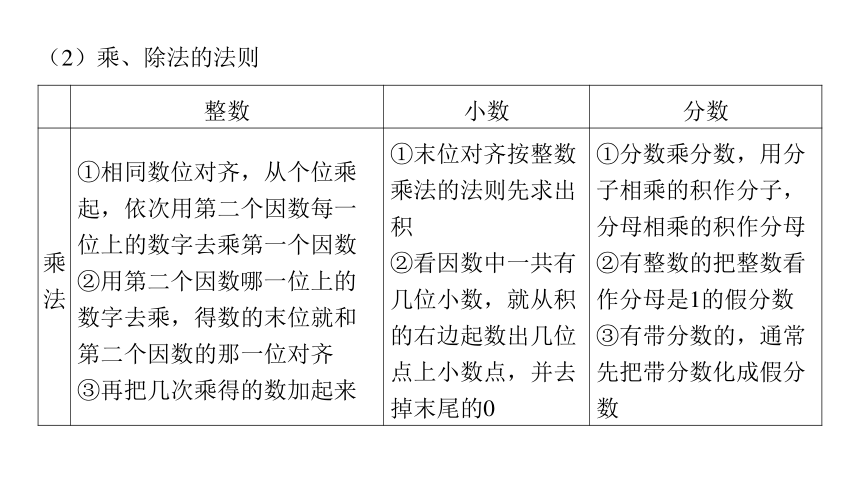
(2)乘、除法的法则
整数 小数 分数
乘 法 ①相同数位对齐,从个位乘
起,依次用第二个因数每一
位上的数字去乘第一个因数 ②用第二个因数哪一位上的
数字去乘,得数的末位就和
第二个因数的那一位对齐 ③再把几次乘得的数加起来 ①末位对齐按整数
乘法的法则先求出
积 ②看因数中一共有
几位小数,就从积
的右边起数出几位
点上小数点,并去
掉末尾的0 ①分数乘分数,用分
子相乘的积作分子,
分母相乘的积作分母
②有整数的把整数看
作分母是1的假分数
③有带分数的,通常
先把带分数化成假分
数
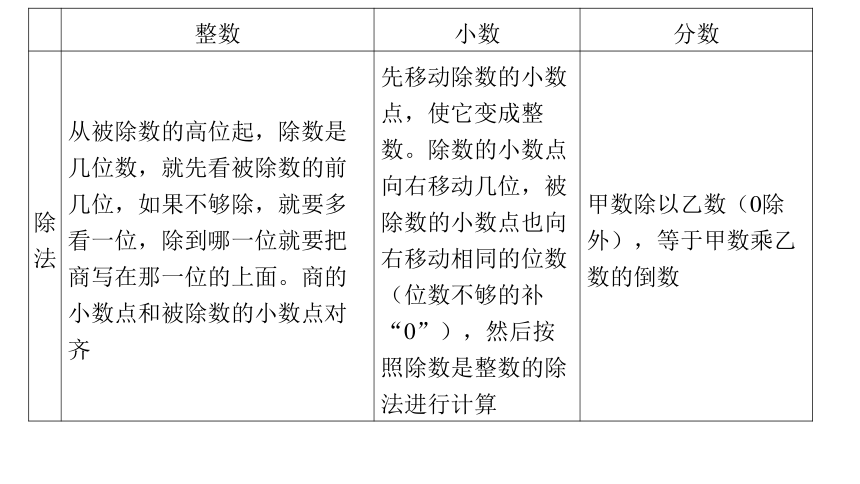
整数 小数 分数
除 法 从被除数的高位起,除数是
几位数,就先看被除数的前
几位,如果不够除,就要多
看一位,除到哪一位就要把
商写在那一位的上面。商的
小数点和被除数的小数点对
齐 先移动除数的小数
点,使它变成整
数。除数的小数点
向右移动几位,被
除数的小数点也向
右移动相同的位数
(位数不够的补
“0”),然后按
照除数是整数的除
法进行计算 甲数除以乙数(0除
外),等于甲数乘乙
数的倒数
温馨提示
1.分数除以整数,当分子能被整数整除时,可直接去除分子,如÷2=
=。这是分数除法的一种特殊情况。
2.分数除以分数,当分子、分母都能整除时,可以把分子、分母分别相
除,如÷==,它与×约分后所得的结果一样。
四则运算的关系
1.加法和减法互为逆运算
2.乘法和除法互为逆运算
温馨提示
在有余数的除法中,余数要比除数小。
3.有余数的除法中各部分之间的关系
被除数=商×除数+余数 除数=(被除数-余数)÷商
智慧锦囊
(m≠0)
a+b=c
(a±m)+b=c±m
(a+m)+(b-m)=c
a-b=c
(a±m)-b=c±m
a-(b±m)=c m
a×b=c
(a×m)×b=c×m
(a×m)×(b÷m)=c
a÷b=c
(a×m)÷(b×m)=c
(a÷m)÷(b÷m)=c
和、差、积、商的变化规律
1.和的变化规律
(1)在一道加法算式里,加数加上(或减去)一个数,和也随着加上(或减
去)同一个数。
(2)在一道加法算式里,一个加数加上一个数,另一个加数减去相同的数,
和不变。
2.差的变化规律
(1)在一道减法算式里,被减数加上(或减去)一个数,差也随着加上(或
减去)同一个数。
(2)在一道减法算式里,减数加上(或减去)一个数,差反而减去(或加
上)同一个数。
3.积的变化规律
(1)在一道乘法算式里,一个因数乘(或除以)一个不为0的数,积也乘
(或除以)这个数。
(2)在一道乘法算式里,一个因数乘(或除以)一个不为0的数,另一个因
数除以(或乘)这个数,积不变。
4.商的变化规律
(1)在一道除法算式里,被除数和除数同时乘(或除以)相同的数(0除
外),商不变。
(2)在计算有余数的除法时,如果被除数和除数扩大(或缩小)到原来的n
倍(或),商不变,但余数也相应扩大(或缩小)到原来的n倍(或)。
5.有关“0”和“1”的计算
(1)一个数加上0或减去0,还得原数。a+0=a,a-0=a。
(2)被减数等于减数,差是0。a-a=0。
(3)一个数和0相乘,仍得0。a×0=0。
(4)0除以一个非0的数,还得0。注意:0不能作除数。0÷a=0(a≠0)。
(5)一个非0的数乘1或除以1,还得原数。a×1=a,a÷1=a。
(6)被除数等于除数(都不为0),商是1。a÷a=1(a≠0)。
温馨提示
1.对整数四则运算结果进行估算时,可以把其中的一个或两个数看作接
近整十、整百的数进行口算。
2.对小数、分数四则运算结果进行估算时,可以把其中的一个或两个数
看作与它接近的整数进行口算。
估算
估算是依据实际问题需要,把参与运算的数估成整十数或整百数再口算出结
果的方法。
典例1
列竖式计算,带★的要验算。
★604-178= 2.85+3.18= ★104÷8= 169×4=
根据整数或小数的加、减、乘、除法的计算法则进行计算,分别用各
自的逆运算进行验算。
426(验算略) 6.03 13(验算略) 676
即时训练1:列竖式计算,带★的要验算。
★10-0.76=9.24(验算略) 2.4÷0.16=15
9.24(验算略)
15
典例2
根据1.71÷0.9=1.9直接写出下面各式的得数。
1.9×0.9=( ) 1.71÷1.9=( )
根据除数×商=被除数,被除数÷商=除数,可以得出结果。
1.71 0.9
即时训练2:不计算,直接根据给出的算式填写下面各式的结果。
24×15=360
(1)360÷24=( 15 ) (2)360÷15=( 24 )
(3)2.4×150=( 360 ) (4)15×240=( 3600 )
(5)3.6÷15=( 0.24 ) (6)3600÷240=( 15 )
15
24
360
3600
0.24
15
典例3
如果a÷b=c……d(a≠0,b≠0),那么10a÷10b=( )……
( )。
被除数a和除数b同时乘10,商不变,但是余数要扩大到原来的10倍。
c 10d
即时训练3:53÷6的商是8,余数是5,则5300÷600的商和余数分别是
( B )。
A.800,500 B.8,500 C.800,5 D.8,5
即时训练 4:两个因数的积是7.6,若一个因数扩大到原来的6倍,另一个因数
缩小到原来的,则积是( 15.2 )。
B
15.2
典例4
a是大于0的数,(a+a)÷a+(a-a)×a的结果是( )。
A.a B.2 C.2-a D.0
此题要求熟练地利用“0”和“1”的计算特点解题。
B
即时训练 5:(1999-0)×(1÷1999)的计算结果是( C )。
A.0 B.1999 C.1 D.3996001
即时训练 6:如果用☆代表同一个非0自然数,下列算式中,得数最大的是
( B )。
A.☆÷ B.☆÷ C.÷☆ D.☆×
C
B
典例5
□96是一个三位数,□96×5的积最接近2000,□里的数字是( )。
根据乘除法之间的关系可知,2000÷5=400,就要把□96估成400。
3
即时训练 7:估算下面各题。
698+301≈1000 1000-597≈400
502-299≈200 498×6≈3000
2.01×7.2≈14 12.03÷3.9≈3
5.98×2.04≈12 809÷89≈9
1000
400
200
3000
14
3
12
9
一、填空。
1.从57.6里连续减去( 18 )个3.2,结果等于0。
2.两个连续自然数的和乘以它们的差,积是39,这两个自然数分别是
( 19 )和( 20 )。
3.整数除法中,一个数除以18,商是25,并有余数,这个数最大是
( 467 )。
4.5.4吨的是( 3.6 )吨,( 8.1 )吨的是5.4吨。
18
19
20
467
3.6
8.1
1.85× < 1.85 ÷ < - =
0.95×2.5 > 0.95 356÷61 < 6 7.2÷0.4 > 7.2×0.4
6.设A,B为自然数,并满足+=,则A+B=( 3 )。
7.根据2.3×3.9=8.97,直接填写下面各题的得数。
0.23×39=( 8.97 ) 2.3×390=( 897 )
23×0.039=( 0.897 ) 89.7÷39=( 2.3 )
8.小明在计算除法时,把一个数除以错看成乘结果得,这道题的正确结果
是( )。
<
<
=
>
<
>
3
8.97
897
0.897
2.3
5.在 里填上“>”“<”或“=”。
二、选择。
1.0.13÷0.06=( A )。
A.2……0.01 B.2……0.1
C.2……1 D.2……100
2.a是非零自然数,a( D )一定大于a。
A.+ B.- C.× D.÷或+
3.观察右边的算式,方框内的数表示( C )。
A.36个1 B.36个0.1
C.36个0.01 D.36个0.001
A
D
C
三、列竖式计算,带★的要验算。(验算略)
★600-297=303 428×57=24396 106÷12=8.8(或8……10)
★43.75+5.625=49.375 0.16÷2.3≈0.07 6.05×15.8≈95.6
(保留两位小数) (精确到十分位)
(验算略)
303
24396
8.8(或8……10)
49.375
0.07
95.6
四、解决问题。
在一道减法算式里,被减数、减数和差相加的和是50。已知差是减数的,差
是多少?
【答案】10
四则运算的意义和法则
四则运算的意义、法则
1.四则运算的意义
运算名称 相关概念与意义
加法 把两个数合并成一个数的运算
相加的数叫作加数,相加的结果叫作和
减法 已知两个加数的和与其中一个加数,求另一个加数的运算
乘法 求几个相同加数和的简便运算。相乘的两数叫因数,相乘的结果
叫积
除法 已知两个因数的积与其中一个因数,求另一个因数的运算
温馨提示
四则运算是“加、减、乘、除”四种运算的统称。
减法是加法的逆运算。
除法是乘法的逆运算。
2.四则运算的法则
(1)加、减法的法则
整数 小数 分数
①相同数位对齐 ②从低位算起 ③加法中满十就向
前一位进一;减法
中不够减时,就从
前一位借一当十 ①相同数位对齐(小数点对
齐) ②从低位算起 ③按整数加、减法的法则进行
计算 ④结果中的小数点和相加、减
的数里的小数点对齐 ①同分母分数相加减,
分母不变,分子相加减
②异分母分数相加减,
先通分然后计算
③结果能约分的要约分
成最简分数
(2)乘、除法的法则
整数 小数 分数
乘 法 ①相同数位对齐,从个位乘
起,依次用第二个因数每一
位上的数字去乘第一个因数 ②用第二个因数哪一位上的
数字去乘,得数的末位就和
第二个因数的那一位对齐 ③再把几次乘得的数加起来 ①末位对齐按整数
乘法的法则先求出
积 ②看因数中一共有
几位小数,就从积
的右边起数出几位
点上小数点,并去
掉末尾的0 ①分数乘分数,用分
子相乘的积作分子,
分母相乘的积作分母
②有整数的把整数看
作分母是1的假分数
③有带分数的,通常
先把带分数化成假分
数
整数 小数 分数
除 法 从被除数的高位起,除数是
几位数,就先看被除数的前
几位,如果不够除,就要多
看一位,除到哪一位就要把
商写在那一位的上面。商的
小数点和被除数的小数点对
齐 先移动除数的小数
点,使它变成整
数。除数的小数点
向右移动几位,被
除数的小数点也向
右移动相同的位数
(位数不够的补
“0”),然后按
照除数是整数的除
法进行计算 甲数除以乙数(0除
外),等于甲数乘乙
数的倒数
温馨提示
1.分数除以整数,当分子能被整数整除时,可直接去除分子,如÷2=
=。这是分数除法的一种特殊情况。
2.分数除以分数,当分子、分母都能整除时,可以把分子、分母分别相
除,如÷==,它与×约分后所得的结果一样。
四则运算的关系
1.加法和减法互为逆运算
2.乘法和除法互为逆运算
温馨提示
在有余数的除法中,余数要比除数小。
3.有余数的除法中各部分之间的关系
被除数=商×除数+余数 除数=(被除数-余数)÷商
智慧锦囊
(m≠0)
a+b=c
(a±m)+b=c±m
(a+m)+(b-m)=c
a-b=c
(a±m)-b=c±m
a-(b±m)=c m
a×b=c
(a×m)×b=c×m
(a×m)×(b÷m)=c
a÷b=c
(a×m)÷(b×m)=c
(a÷m)÷(b÷m)=c
和、差、积、商的变化规律
1.和的变化规律
(1)在一道加法算式里,加数加上(或减去)一个数,和也随着加上(或减
去)同一个数。
(2)在一道加法算式里,一个加数加上一个数,另一个加数减去相同的数,
和不变。
2.差的变化规律
(1)在一道减法算式里,被减数加上(或减去)一个数,差也随着加上(或
减去)同一个数。
(2)在一道减法算式里,减数加上(或减去)一个数,差反而减去(或加
上)同一个数。
3.积的变化规律
(1)在一道乘法算式里,一个因数乘(或除以)一个不为0的数,积也乘
(或除以)这个数。
(2)在一道乘法算式里,一个因数乘(或除以)一个不为0的数,另一个因
数除以(或乘)这个数,积不变。
4.商的变化规律
(1)在一道除法算式里,被除数和除数同时乘(或除以)相同的数(0除
外),商不变。
(2)在计算有余数的除法时,如果被除数和除数扩大(或缩小)到原来的n
倍(或),商不变,但余数也相应扩大(或缩小)到原来的n倍(或)。
5.有关“0”和“1”的计算
(1)一个数加上0或减去0,还得原数。a+0=a,a-0=a。
(2)被减数等于减数,差是0。a-a=0。
(3)一个数和0相乘,仍得0。a×0=0。
(4)0除以一个非0的数,还得0。注意:0不能作除数。0÷a=0(a≠0)。
(5)一个非0的数乘1或除以1,还得原数。a×1=a,a÷1=a。
(6)被除数等于除数(都不为0),商是1。a÷a=1(a≠0)。
温馨提示
1.对整数四则运算结果进行估算时,可以把其中的一个或两个数看作接
近整十、整百的数进行口算。
2.对小数、分数四则运算结果进行估算时,可以把其中的一个或两个数
看作与它接近的整数进行口算。
估算
估算是依据实际问题需要,把参与运算的数估成整十数或整百数再口算出结
果的方法。
典例1
列竖式计算,带★的要验算。
★604-178= 2.85+3.18= ★104÷8= 169×4=
根据整数或小数的加、减、乘、除法的计算法则进行计算,分别用各
自的逆运算进行验算。
426(验算略) 6.03 13(验算略) 676
即时训练1:列竖式计算,带★的要验算。
★10-0.76=9.24(验算略) 2.4÷0.16=15
9.24(验算略)
15
典例2
根据1.71÷0.9=1.9直接写出下面各式的得数。
1.9×0.9=( ) 1.71÷1.9=( )
根据除数×商=被除数,被除数÷商=除数,可以得出结果。
1.71 0.9
即时训练2:不计算,直接根据给出的算式填写下面各式的结果。
24×15=360
(1)360÷24=( 15 ) (2)360÷15=( 24 )
(3)2.4×150=( 360 ) (4)15×240=( 3600 )
(5)3.6÷15=( 0.24 ) (6)3600÷240=( 15 )
15
24
360
3600
0.24
15
典例3
如果a÷b=c……d(a≠0,b≠0),那么10a÷10b=( )……
( )。
被除数a和除数b同时乘10,商不变,但是余数要扩大到原来的10倍。
c 10d
即时训练3:53÷6的商是8,余数是5,则5300÷600的商和余数分别是
( B )。
A.800,500 B.8,500 C.800,5 D.8,5
即时训练 4:两个因数的积是7.6,若一个因数扩大到原来的6倍,另一个因数
缩小到原来的,则积是( 15.2 )。
B
15.2
典例4
a是大于0的数,(a+a)÷a+(a-a)×a的结果是( )。
A.a B.2 C.2-a D.0
此题要求熟练地利用“0”和“1”的计算特点解题。
B
即时训练 5:(1999-0)×(1÷1999)的计算结果是( C )。
A.0 B.1999 C.1 D.3996001
即时训练 6:如果用☆代表同一个非0自然数,下列算式中,得数最大的是
( B )。
A.☆÷ B.☆÷ C.÷☆ D.☆×
C
B
典例5
□96是一个三位数,□96×5的积最接近2000,□里的数字是( )。
根据乘除法之间的关系可知,2000÷5=400,就要把□96估成400。
3
即时训练 7:估算下面各题。
698+301≈1000 1000-597≈400
502-299≈200 498×6≈3000
2.01×7.2≈14 12.03÷3.9≈3
5.98×2.04≈12 809÷89≈9
1000
400
200
3000
14
3
12
9
一、填空。
1.从57.6里连续减去( 18 )个3.2,结果等于0。
2.两个连续自然数的和乘以它们的差,积是39,这两个自然数分别是
( 19 )和( 20 )。
3.整数除法中,一个数除以18,商是25,并有余数,这个数最大是
( 467 )。
4.5.4吨的是( 3.6 )吨,( 8.1 )吨的是5.4吨。
18
19
20
467
3.6
8.1
1.85× < 1.85 ÷ < - =
0.95×2.5 > 0.95 356÷61 < 6 7.2÷0.4 > 7.2×0.4
6.设A,B为自然数,并满足+=,则A+B=( 3 )。
7.根据2.3×3.9=8.97,直接填写下面各题的得数。
0.23×39=( 8.97 ) 2.3×390=( 897 )
23×0.039=( 0.897 ) 89.7÷39=( 2.3 )
8.小明在计算除法时,把一个数除以错看成乘结果得,这道题的正确结果
是( )。
<
<
=
>
<
>
3
8.97
897
0.897
2.3
5.在 里填上“>”“<”或“=”。
二、选择。
1.0.13÷0.06=( A )。
A.2……0.01 B.2……0.1
C.2……1 D.2……100
2.a是非零自然数,a( D )一定大于a。
A.+ B.- C.× D.÷或+
3.观察右边的算式,方框内的数表示( C )。
A.36个1 B.36个0.1
C.36个0.01 D.36个0.001
A
D
C
三、列竖式计算,带★的要验算。(验算略)
★600-297=303 428×57=24396 106÷12=8.8(或8……10)
★43.75+5.625=49.375 0.16÷2.3≈0.07 6.05×15.8≈95.6
(保留两位小数) (精确到十分位)
(验算略)
303
24396
8.8(或8……10)
49.375
0.07
95.6
四、解决问题。
在一道减法算式里,被减数、减数和差相加的和是50。已知差是减数的,差
是多少?
【答案】10
同课章节目录
