1.2.4绝对值1
图片预览

文档简介
教学设计
章节名称 1.2.4 绝对值-1 学时 1
课标要求 1.借助数轴理解绝对值的意义 2.能求一个数的绝对值
内容与学情分析 内容分析 “绝对值”是“距离”这一几何量的代数表示.距离是基本而重要的几何概念,相应地,绝对值是基本而重要的代数概念. 借助数轴给出绝对值的定义,直观而利 于学生理解由此得出一个正数、负数或0的绝对值各是什么的结论也水到渠成,并且可以用字母简明地把这些结论表示出来,需要提醒学生注意,由于“距离”不可能是负数,因此一个数的绝对值也不可能是负数.
教学重点 绝对值含义的理解,求已知数的绝对值,掌握绝对值表示方法
教学难点 理解绝对值的几何意义
学情分析 学生本阶段具有好动,注意力易分散,爱发表见解,希望得到老师的表扬等特点,所以在教学中一方面要运用多媒体课件,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面要创造条件和机会,让学生发表见解,发挥学生学习的主动性。 学生已学习了有理数,数轴等基础内容,这为过渡到本节的学习起着铺垫作用。相反数、绝对值不仅可以使学生加深对有理数的认识,还为学习两个负数的大小比较以及有理数的运算作好必要的准备!
教学目标 1、借助数轴与绝对值初步理解绝对值的概念 熟悉绝对值的符号 能求一个数的绝对值
学生课前需要做的准备工作 预习课本
教学策略 自主探索、合作探究
课程资源 人教版教材与教师用书
教学环节 学习任务设计 与教师活动 学生活动设计 设计意图 落实目标
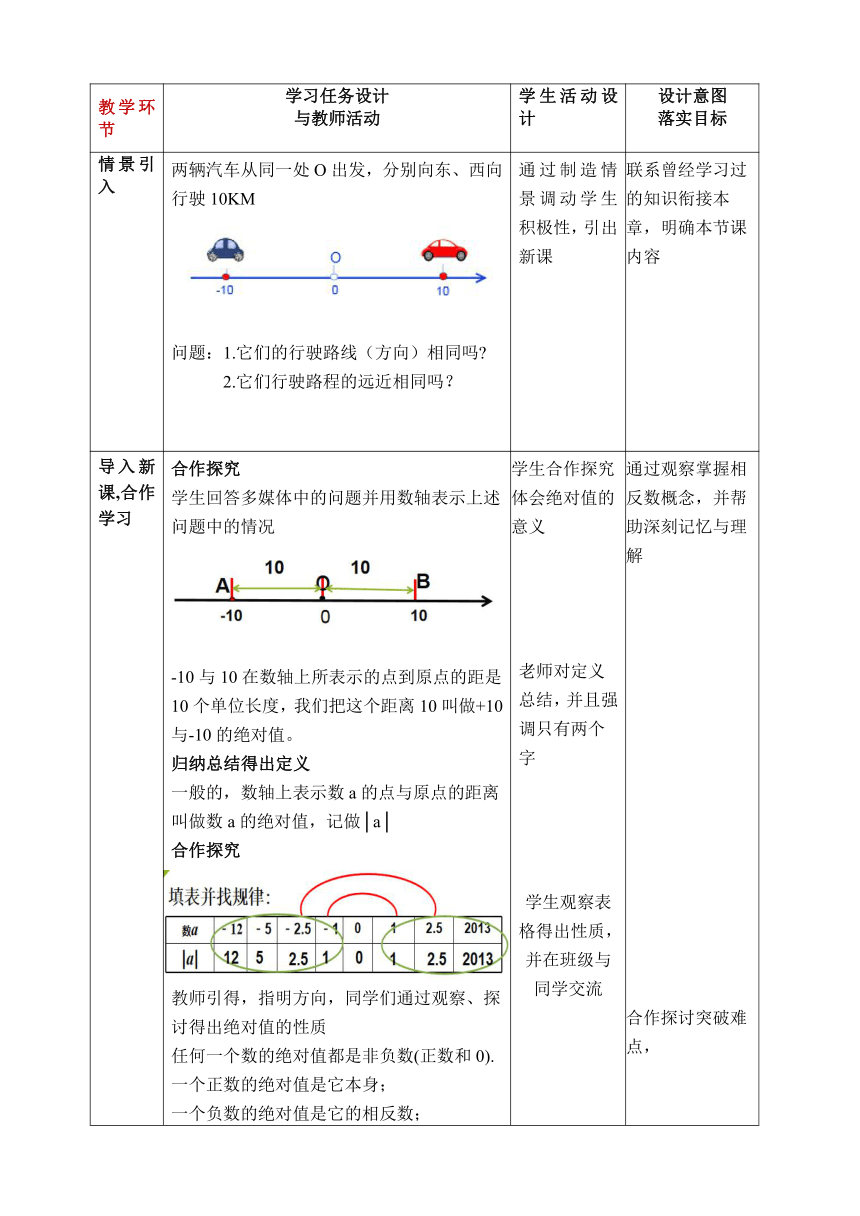
情景引入 两辆汽车从同一处O出发,分别向东、西向行驶10KM 问题:1.它们的行驶路线(方向)相同吗 2.它们行驶路程的远近相同吗? 通过制造情景调动学生积极性,引出新课 联系曾经学习过的知识衔接本章,明确本节课内容
导入新课,合作学习 合作探究 学生回答多媒体中的问题并用数轴表示上述 问题中的情况 -10与10在数轴上所表示的点到原点的距是 10个单位长度,我们把这个距离10叫做+10 与-10的绝对值。 归纳总结得出定义 一般的,数轴上表示数a的点与原点的距离 叫做数a的绝对值,记做│a│ 合作探究 教师引得,指明方向,同学们通过观察、探 讨得出绝对值的性质 任何一个数的绝对值都是非负数(正数和0). 一个正数的绝对值是它本身; 一个负数的绝对值是它的相反数; 0的绝对值是0. 互为相反数的两个数,其绝对值相等. 教师引导,将绝对值的几何意义用数学符号 的形式表现出来,同样加深学生对绝对值意 义的理解 学生合作探究体会绝对值的意义 老师对定义总结,并且强调只有两个字 学生观察表格得出性质,并在班级与同学交流 在老师引导下得出绝对值性质,并会用符号表示性质 通过观察掌握相反数概念,并帮助深刻记忆与理解 合作探讨突破难点, 识记、理解相关概念
范例精讲 课外例题 1.判断下列说法是否正确: (1)一个数的绝对值越大,表示它的点在数轴上越靠右 (2)一个数的绝对值越大,表示它的点在数轴上离原点越远 (3)当a≠0,│a│总大于0 2、 │6│= │-100│= │0│=
当堂训练 1.课本练习 2补充: .写出下列各数的绝对值: -125 , +2.3 , -0.15, 0, -2/3 ,3/2,-1/2 2、.已知│a│=2 求a 3、若整数a,b满足等式, 求a+b的值 分析;若几个非负数的和等于0,则这几个非负数同时为0 因为 所以a-3=0 ,b-2=0 所以a=3,b=2 所以a+b=3+2=5 解后反思: 绝对值具有非负性,即若│a│+│b│=0, 则必有 a=b=0 学生独立完成,教师巡视指导,了解学生掌握情况,并集中订正 使学生巩固提高,了解学生掌握情况
小结 掌握绝对值的定义及几何意义 掌握绝对值的性质
作业 1.教材习题1.2 5 、10、 12。 2.作业单。
板书设计 1.2.4绝对值 绝对值定义: 符号; 符号表示:
反思
章节名称 1.2.4 绝对值-1 学时 1
课标要求 1.借助数轴理解绝对值的意义 2.能求一个数的绝对值
内容与学情分析 内容分析 “绝对值”是“距离”这一几何量的代数表示.距离是基本而重要的几何概念,相应地,绝对值是基本而重要的代数概念. 借助数轴给出绝对值的定义,直观而利 于学生理解由此得出一个正数、负数或0的绝对值各是什么的结论也水到渠成,并且可以用字母简明地把这些结论表示出来,需要提醒学生注意,由于“距离”不可能是负数,因此一个数的绝对值也不可能是负数.
教学重点 绝对值含义的理解,求已知数的绝对值,掌握绝对值表示方法
教学难点 理解绝对值的几何意义
学情分析 学生本阶段具有好动,注意力易分散,爱发表见解,希望得到老师的表扬等特点,所以在教学中一方面要运用多媒体课件,引发学生的兴趣,使他们的注意力始终集中在课堂上;另一方面要创造条件和机会,让学生发表见解,发挥学生学习的主动性。 学生已学习了有理数,数轴等基础内容,这为过渡到本节的学习起着铺垫作用。相反数、绝对值不仅可以使学生加深对有理数的认识,还为学习两个负数的大小比较以及有理数的运算作好必要的准备!
教学目标 1、借助数轴与绝对值初步理解绝对值的概念 熟悉绝对值的符号 能求一个数的绝对值
学生课前需要做的准备工作 预习课本
教学策略 自主探索、合作探究
课程资源 人教版教材与教师用书
教学环节 学习任务设计 与教师活动 学生活动设计 设计意图 落实目标
情景引入 两辆汽车从同一处O出发,分别向东、西向行驶10KM 问题:1.它们的行驶路线(方向)相同吗 2.它们行驶路程的远近相同吗? 通过制造情景调动学生积极性,引出新课 联系曾经学习过的知识衔接本章,明确本节课内容
导入新课,合作学习 合作探究 学生回答多媒体中的问题并用数轴表示上述 问题中的情况 -10与10在数轴上所表示的点到原点的距是 10个单位长度,我们把这个距离10叫做+10 与-10的绝对值。 归纳总结得出定义 一般的,数轴上表示数a的点与原点的距离 叫做数a的绝对值,记做│a│ 合作探究 教师引得,指明方向,同学们通过观察、探 讨得出绝对值的性质 任何一个数的绝对值都是非负数(正数和0). 一个正数的绝对值是它本身; 一个负数的绝对值是它的相反数; 0的绝对值是0. 互为相反数的两个数,其绝对值相等. 教师引导,将绝对值的几何意义用数学符号 的形式表现出来,同样加深学生对绝对值意 义的理解 学生合作探究体会绝对值的意义 老师对定义总结,并且强调只有两个字 学生观察表格得出性质,并在班级与同学交流 在老师引导下得出绝对值性质,并会用符号表示性质 通过观察掌握相反数概念,并帮助深刻记忆与理解 合作探讨突破难点, 识记、理解相关概念
范例精讲 课外例题 1.判断下列说法是否正确: (1)一个数的绝对值越大,表示它的点在数轴上越靠右 (2)一个数的绝对值越大,表示它的点在数轴上离原点越远 (3)当a≠0,│a│总大于0 2、 │6│= │-100│= │0│=
当堂训练 1.课本练习 2补充: .写出下列各数的绝对值: -125 , +2.3 , -0.15, 0, -2/3 ,3/2,-1/2 2、.已知│a│=2 求a 3、若整数a,b满足等式, 求a+b的值 分析;若几个非负数的和等于0,则这几个非负数同时为0 因为 所以a-3=0 ,b-2=0 所以a=3,b=2 所以a+b=3+2=5 解后反思: 绝对值具有非负性,即若│a│+│b│=0, 则必有 a=b=0 学生独立完成,教师巡视指导,了解学生掌握情况,并集中订正 使学生巩固提高,了解学生掌握情况
小结 掌握绝对值的定义及几何意义 掌握绝对值的性质
作业 1.教材习题1.2 5 、10、 12。 2.作业单。
板书设计 1.2.4绝对值 绝对值定义: 符号; 符号表示:
反思
