人教版八年级下册16.1.1 二次根式的概念 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级下册16.1.1 二次根式的概念 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 331.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第十六章
二次根式
八年级数学人教统编版·下册
16.1.1 二次根式的概念
教学目标
1.了解二次根式的概念 , 理解二次根式有意义的条件 ;(重点)
2.会求二次根式中字母的取值范围 .(难点)
问题1 什么叫做平方根
一般地 , 如果一个数的平方等于a , 那么这个数叫做 a 的平方根 .
问题2 什么叫做算术平方根
如果 x2 = a ( x≥0 ) , 那么 x 称为 a 的算术平方根 . 用 表示 .
问题3 什么数有算术平方根
我们知道 , 负数没有平方根 . 因此 , 在实数范围内开平方时 , 被开方数只能是正数或0 .
新课导入
1.下列选项中 , 使根式有意义的 a 的取值范围为 a<1 的是 ( )
2.填空:
(1) 9的平方根是_______; (2) 64的算术平方根是_______;
(3) 0的算术平方根是_______;
(4) a (a≥0)的平方根是_______.
D
±3
8
0
新课导入
新课导入
唐僧师徒在万寿山五庄观做客 . 猪八戒来到后花园 , 看见人参果树上结满了人参果 , 嘴馋得直流口水 . 正准备伸手摘时 , 突然一道金光 , 在同一个枝头上一大一小的两个果子同时掉了下来 , 噗的一声同时着地 . 有爱好数学的电视迷算了人参果下落的时间 t 与 h之间的关系式为 t= , 你觉得他算的正确吗
知识归纳
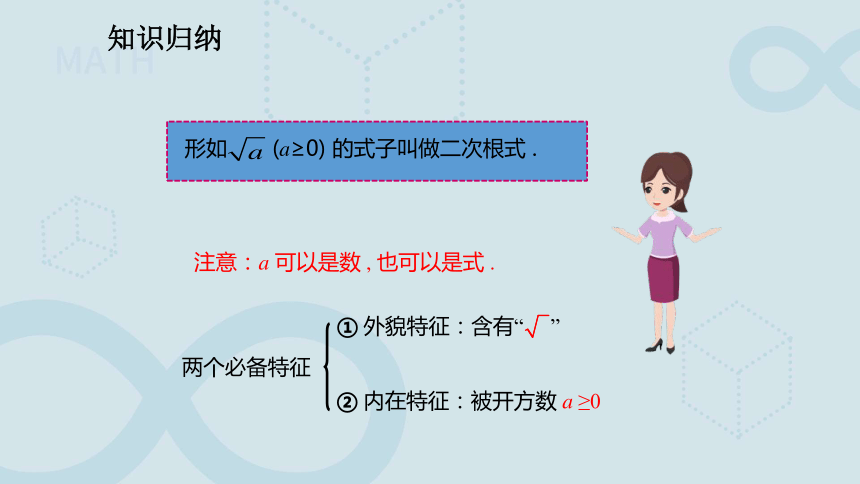
形如 (a≥0) 的式子叫做二次根式 .
两个必备特征
① 外貌特征:含有“ ”
② 内在特征:被开方数 a ≥0
注意:a 可以是数 , 也可以是式 .
新知探究
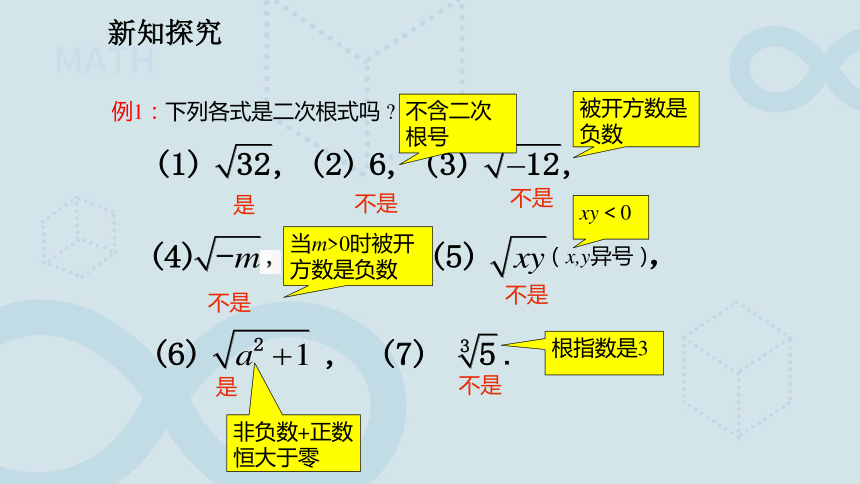
例1:下列各式是二次根式吗
是
不是
不是
(x,y异号)
不是
不是
是
不是
不含二次根号
被开方数是负数
当m>0时被开方数是负数
xy<0
非负数+正数恒大于零
根指数是3
.
新知探究
例2 : 下列各式中 , 哪些是二次根式 并指出二次根式中的被开
方数 .
解: >0) 是二次根式.
其中被开方数依次是7 , x-3 , (x+1)2 ,
新知探究
例3 : 当 x 是怎样的实数时 , 二次根式 在实数范围内有意义
解:由 x-2≥0 , 得
x≥2 .
当 x≥2 时 , 在实数范围内有意义 .
变式题:当 x 是怎样的实数时 , 下列各式在实数范围内有意义
解:由题意得 x-1>0 ,
∴x>1 .
解:∵被开方数需大于或等于零 ,
∴3+x≥0 , ∴x≥-3 .
∵分母不能等于零 , ∴x-1≠0 , ∴x≠1 .
∴x≥-3 且x≠1 .
知识归纳
要使二次根式在实数范围内有意义 , 即需满足被开方数 ≥0 , 列不等式求解即可 . 若二次根式或含未知数的式子为分式的分母时 , 应同时考虑分母不为零 .
新知探究
(1) 单个二次根式如 有意义的条件 : A≥0 ;
(2) 多个二次根式相加如 有意义的
条件:
(3) 二次根式作为分式的分母如 有意义的条件 :
A>0 ;
(4) 二次根式与分式的和如 有意义的条件:
A≥0 且 B≠0 .
归纳总结
新知探究
例4 : 若 ; 求 a -b+c 的值 .
解:
由题意可知 a-2=0 , b-3=0 , c-4=0 ,
解得 a=2 , b=3 , c=4 .
所以 a-b+c=2-3+4=3 .
新知探究
例5 : 已知 y= , 求 3x+2y 的算术平方根 .
解 : 由题意得
∴ x=3 , ∴y=8 ,
∴ 3x+2y=25 .
∵ 25的算术平方根为5 ,
∴3x+2y 的算术平方根为5 .
课堂小结
二次根式概念:
形如 ( a≥0 ) 的式子叫做二次根式
要使二次根式在实数范围内有意义 , 即需满足被开方数≥0 , 列不等式求解即可 .若二次根式或含未知数的式子为分式的分母时 , 应同时考虑分母不为零
课堂小测
1.下列各式: .
一定是二次根式的个数有 ( )
A.3个 B.4个 C.5个 D.6个
B
2.(1) 若式子 在实数范围内有意义 , 则 x 的取值
范围是_______;
(2) 若式子 在实数范围内有意义 , 则 x 的
取值范围是____________.
x ≥1
x ≥0 且 x≠2
课堂小测
3.式子 有意义的条件是 ( )
A.x>2 B.x≥2 C.x<2 D.x≤2
4.若 是整数 , 则自然数 n 的值有 ( )
A.7个 B.8个 C.9个 D.10个
D
A
课堂小测
5.当 x 为何值时 , 在实数范围内有意义
解 : 要使式子在实数范围内有意义 , 必须同时满足被开方数
x+3≥0 和分母 x+1≠0 , 解得 x≥-3 且 x≠-1 .
课堂小测
6.求下列各式中字母 a 的取值范围 :
解 : 由 a+1≥0 , 得 a≥-1 .
∴ 字母 a 的取值范围是大于或等于-1的实数 .
解:由 >0 , 得 1-2a>0 , 即a < ,
∴字母 a 的取值范围是小于 的实数 .
;
;
课堂小测
解 : 因为无论 a 取何值 , 都有 (a-3)2≥0 ,
所以字母 a 的取值范围是全体实数 .
解:因为无论 a 取何值 , 都有 |a|+1>0 ,
所以字母 a 的取值范围是全体实数 .
;
.
7.已知 |3x-y-1| 和 互为相反数 , 求 x+4y 的平方根 .
解:由题意得 3x-y-1=0 且 2x+y-4=0 .
解得x=1 , y=2 .
∴ x+4y=1+2×4=9 .
∴ x+4y 的平方根为±3 .
课堂小测
第十六章
二次根式
八年级数学人教统编版·下册
16.1.1 二次根式的概念
教学目标
1.了解二次根式的概念 , 理解二次根式有意义的条件 ;(重点)
2.会求二次根式中字母的取值范围 .(难点)
问题1 什么叫做平方根
一般地 , 如果一个数的平方等于a , 那么这个数叫做 a 的平方根 .
问题2 什么叫做算术平方根
如果 x2 = a ( x≥0 ) , 那么 x 称为 a 的算术平方根 . 用 表示 .
问题3 什么数有算术平方根
我们知道 , 负数没有平方根 . 因此 , 在实数范围内开平方时 , 被开方数只能是正数或0 .
新课导入
1.下列选项中 , 使根式有意义的 a 的取值范围为 a<1 的是 ( )
2.填空:
(1) 9的平方根是_______; (2) 64的算术平方根是_______;
(3) 0的算术平方根是_______;
(4) a (a≥0)的平方根是_______.
D
±3
8
0
新课导入
新课导入
唐僧师徒在万寿山五庄观做客 . 猪八戒来到后花园 , 看见人参果树上结满了人参果 , 嘴馋得直流口水 . 正准备伸手摘时 , 突然一道金光 , 在同一个枝头上一大一小的两个果子同时掉了下来 , 噗的一声同时着地 . 有爱好数学的电视迷算了人参果下落的时间 t 与 h之间的关系式为 t= , 你觉得他算的正确吗
知识归纳
形如 (a≥0) 的式子叫做二次根式 .
两个必备特征
① 外貌特征:含有“ ”
② 内在特征:被开方数 a ≥0
注意:a 可以是数 , 也可以是式 .
新知探究
例1:下列各式是二次根式吗
是
不是
不是
(x,y异号)
不是
不是
是
不是
不含二次根号
被开方数是负数
当m>0时被开方数是负数
xy<0
非负数+正数恒大于零
根指数是3
.
新知探究
例2 : 下列各式中 , 哪些是二次根式 并指出二次根式中的被开
方数 .
解: >0) 是二次根式.
其中被开方数依次是7 , x-3 , (x+1)2 ,
新知探究
例3 : 当 x 是怎样的实数时 , 二次根式 在实数范围内有意义
解:由 x-2≥0 , 得
x≥2 .
当 x≥2 时 , 在实数范围内有意义 .
变式题:当 x 是怎样的实数时 , 下列各式在实数范围内有意义
解:由题意得 x-1>0 ,
∴x>1 .
解:∵被开方数需大于或等于零 ,
∴3+x≥0 , ∴x≥-3 .
∵分母不能等于零 , ∴x-1≠0 , ∴x≠1 .
∴x≥-3 且x≠1 .
知识归纳
要使二次根式在实数范围内有意义 , 即需满足被开方数 ≥0 , 列不等式求解即可 . 若二次根式或含未知数的式子为分式的分母时 , 应同时考虑分母不为零 .
新知探究
(1) 单个二次根式如 有意义的条件 : A≥0 ;
(2) 多个二次根式相加如 有意义的
条件:
(3) 二次根式作为分式的分母如 有意义的条件 :
A>0 ;
(4) 二次根式与分式的和如 有意义的条件:
A≥0 且 B≠0 .
归纳总结
新知探究
例4 : 若 ; 求 a -b+c 的值 .
解:
由题意可知 a-2=0 , b-3=0 , c-4=0 ,
解得 a=2 , b=3 , c=4 .
所以 a-b+c=2-3+4=3 .
新知探究
例5 : 已知 y= , 求 3x+2y 的算术平方根 .
解 : 由题意得
∴ x=3 , ∴y=8 ,
∴ 3x+2y=25 .
∵ 25的算术平方根为5 ,
∴3x+2y 的算术平方根为5 .
课堂小结
二次根式概念:
形如 ( a≥0 ) 的式子叫做二次根式
要使二次根式在实数范围内有意义 , 即需满足被开方数≥0 , 列不等式求解即可 .若二次根式或含未知数的式子为分式的分母时 , 应同时考虑分母不为零
课堂小测
1.下列各式: .
一定是二次根式的个数有 ( )
A.3个 B.4个 C.5个 D.6个
B
2.(1) 若式子 在实数范围内有意义 , 则 x 的取值
范围是_______;
(2) 若式子 在实数范围内有意义 , 则 x 的
取值范围是____________.
x ≥1
x ≥0 且 x≠2
课堂小测
3.式子 有意义的条件是 ( )
A.x>2 B.x≥2 C.x<2 D.x≤2
4.若 是整数 , 则自然数 n 的值有 ( )
A.7个 B.8个 C.9个 D.10个
D
A
课堂小测
5.当 x 为何值时 , 在实数范围内有意义
解 : 要使式子在实数范围内有意义 , 必须同时满足被开方数
x+3≥0 和分母 x+1≠0 , 解得 x≥-3 且 x≠-1 .
课堂小测
6.求下列各式中字母 a 的取值范围 :
解 : 由 a+1≥0 , 得 a≥-1 .
∴ 字母 a 的取值范围是大于或等于-1的实数 .
解:由 >0 , 得 1-2a>0 , 即a < ,
∴字母 a 的取值范围是小于 的实数 .
;
;
课堂小测
解 : 因为无论 a 取何值 , 都有 (a-3)2≥0 ,
所以字母 a 的取值范围是全体实数 .
解:因为无论 a 取何值 , 都有 |a|+1>0 ,
所以字母 a 的取值范围是全体实数 .
;
.
7.已知 |3x-y-1| 和 互为相反数 , 求 x+4y 的平方根 .
解:由题意得 3x-y-1=0 且 2x+y-4=0 .
解得x=1 , y=2 .
∴ x+4y=1+2×4=9 .
∴ x+4y 的平方根为±3 .
课堂小测
