5.3 平行线的性质课件(共49张PPT)
文档属性
| 名称 | 5.3 平行线的性质课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 00:00:00 | ||
图片预览










文档简介
(共49张PPT)
人教版数学七年级下册
第五章 相交线与平行线
5.3 平行线的性质
5.3.1 平行线的性质
导入新课
回顾
窗户内窗的两条竖直的边是平行的,在推动过程中,两条竖直的边与窗户外框形成的两个角∠1,∠2有什么数量关系?
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
探究新知
知识点
平行线
两条平行线被第三条直线截得的同位角具有怎样的数量关系?
思考
如图,已知直线 a∥b ,c 是截线.
b
a
c
1
2
3
4
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
探究
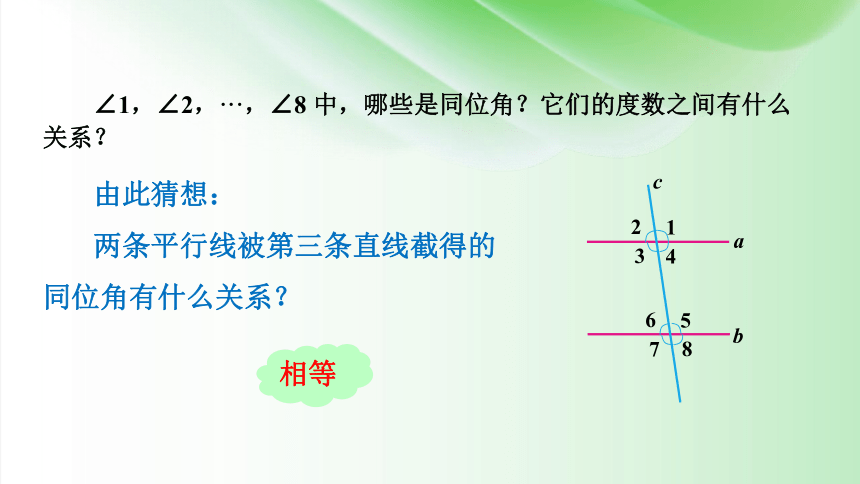
∠1,∠2,···,∠8 中,哪些是同位角?它们的度数之间有什么关系?
由此猜想:
两条平行线被第三条直线截得的同位角有什么关系?
相等
b
a
c
1
2
3
4
5
6
7
8
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
b
a
c
1
2
3
4
5
6
7
8
d
成立
性质 1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
思考
如图,直线 a∥b ,c 是截线,那么 1 与 2 相等吗?为什么?
根据“两直线平行,同位角相等”,可得∠2 = ∠3 .
而∠3 与∠1 互为对顶角,所以∠3 =∠1.
所以∠1 = ∠2.
b
a
c
3
2
1
性质 2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
性质 3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
类似地,
知识归纳
平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
例题与练习
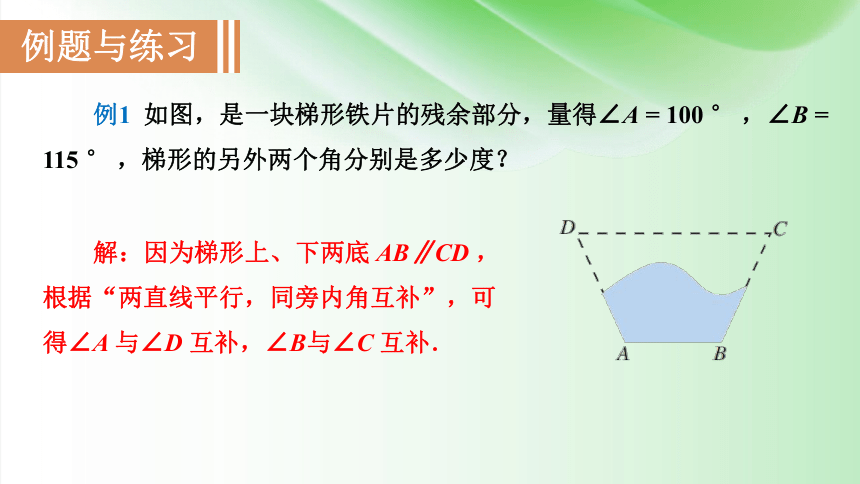
例1 如图,是一块梯形铁片的残余部分,量得∠A = 100 ° ,∠B = 115 ° ,梯形的另外两个角分别是多少度?
解:因为梯形上、下两底 AB∥CD ,根据“两直线平行,同旁内角互补”,可得∠A 与∠D 互补,∠B与∠C 互补.
于是∠D = 180 ° -∠A
= 180 ° -100 = 80 ° ,
∠C = 180 ° -∠B
= 180 ° -115 ° = 65 ° .
所以,梯形的另外两个角分别是 80 ° ,65°.
例2
如图,已知DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
解:∵FG∥EC,
∴∠CAG=∠ACE=36°,
∴∠PAC=∠CAG+∠PAG=36°+12°=48°.
∵AP平分∠BAC,
∴∠BAP=∠PAC=48°.
∵DB∥FG,
∴∠ABD=∠BAG=∠BAP+∠PAG=48°+12°=60°.
例3 如图,已知AB∥CD,直线EF分别交AB,CD于点M,N,MP平分∠EMA,NQ平分∠MNC,那么MP∥NQ,为什么?
解:∵AB∥CD,
∴∠EMA=∠MNC.
∵MP平分∠EMA,NQ平分∠MNC,∴∠EMP= ∠EMA,∠MNQ= ∠MNC,∴∠EMP=∠MNQ,∴MP∥NQ.
例题与练习
练习
1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4 各是多少度?
解:∵a∥b,∠1=54°,∴∠4 =∠1 = 54°(两直线平行,同位角相等).
∠3 =180°-∠4
=180° - 54°=126°,
∠2 与∠1 是对顶角,
∴∠2=∠1= 54°.
2. 如图,在△ABC 中,D 是 AB 上一点,E 是 AC 上一点, ∠ADE = 60°,∠B = 60°,∠AED = 40°.
(1)DE 与 BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
解:(1)∵∠ADE = ∠B,∴DE∥BC(同位角相等,两直线平行)
(2)∵DE∥BC,
∴∠C = ∠AED = 40°(两直线平行,同位角相等)
3.下列图形中,根据AB∥CD,能得到∠1=∠2的是( )
B
4.如图,若∠1+∠2=180°,∠3=110°,则∠4=_______.
110°
5.如图,CD⊥AB于点D,E是BC上一点,EF⊥AB于点F,∠1=∠2,试说明∠AGD=∠ACB的理由.
解:∵CD⊥AB,EF⊥AB,
∴∠EFB=∠CDB=90°,
∴CD∥EF,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴DG∥BC,∴∠AGD=∠ACB.
课堂小结
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
人教版数学七年级下册
第五章 相交线与平行线
5.3 平行线的性质
5.3.2 命题、定理、证明
导入新课
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
回顾
平行线的判定和性质
2.如图,直线a,b被直线c所截,则下列说法正确的是( )
思考完成并交流展示.
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠2-∠1=90°
D.当∠1+∠2=180°时,一定有a∥b
D
探究新知
知识点
命题
(1)如果两条直线都与第三条直线平行,那 么这两条直线也互相平行;
(2)两条平行线被第三条直线所截,同旁内 角互补;
(3)对顶角相等;
(4)等式两边都加同一个数,结果仍是等式.
像这样判断一件事情的语句,叫做命题(proposition).
思考
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
(2)两条平行线被第三条直线所截,同旁内角互补.
(3)如果两个角的和是 90 ,那么这两个角互余.
(4)等式两边都加同一个数, 结果仍是等式.
(5)两点之间,线段最短.
下列各组命题是由几部分组成的?
命题的结构
命题由题设和结论两部分组成.
许多数学命题常可以写成“如果……,那么……”的形式.“如果”后面连接的部分是题设,“那么”后面连接的部分是结论.
已知事项
由已知事项推出的事项
上面练习题中哪些命题是正确的,哪些命题是错误的?
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
√
×
×
√
√
思考
命题的真假
真命题:
假命题:
如果题设成立,那么结论一定成立,这样的命题叫做真命题.
如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
练习
1. 指出下列命题的题设和结论:
(1)如果 AB⊥CD ,垂足为 O ,那么∠AOC = 90°.
题设:如果 AB⊥CD ,垂足为 O ,结论:∠AOC = 90°.
(2)如果∠1=∠2,∠2=∠3,那么∠1=∠3.
题设:如果∠1=∠2,∠2=∠3,结论:∠1=∠3.
题设:如果两条直线平行,结论:同位角相等.
(3)两直线平行,同位角相等.
2.判断下列命题哪些是真命题?哪些是假命题?
(1)在同一平面内,如果一条直线垂直于两 条平行线中的一条,那么也垂直于另一条;
(2)如果两个角互补,那么它们是邻补角;
(3)如果 | a | = | b |,那么 a = b ;
(4)经过直线外一点有且只有一条直线与这 条直线平行;
(5)两点确定一条直线.
真命题
假命题
假命题
真命题
真命题
知识点
定理与证明
上面练习第 2 题中的(1)(4)(5)它们的正确性是经过推理证实的,这样得到的真命题叫做定理(theorem).
定理也可以作为继续推理的依据.
在很多情况下,一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
命题 1 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
请判断下列两个命题的真假,并思考如何判断命题的真假.
命题 2 相等的角是对顶角.
题设:
命题 1:在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
(1)这个命题的题设和结论分别是什么呢?
结论:
在同一平面内,一条直线垂直于两条平行线中的一条;
这条直线也垂直于两条平行线中的另一条.
(2)命题 1 是真命题还是假命题?
真命题
命题 1:在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
(3)你能画出图形,写出已知、求证并证明它是真命题吗?
已知:b∥c, a⊥b .
求证:a⊥c.
b
c
a
证明:∵ a⊥b(已知),
∴∠1 = 90 (垂直的定义).
又∵ b∥c(已知),
∴∠1 = ∠2(两直线平行,同位角相等).
∴∠2 = ∠1 = 90 (等量代换).
∴ a⊥c(垂直的定义).
1
b
2
c
a
例 如图,已知:直线 b∥c,a⊥b. 求证:a⊥c.
归纳
证明中的每一步推理都要有根据,这些根据可以是已知条件,也可以是定义、基本事实、定理等.
题设:
(1)这个命题的题设和结论分别是什么呢?
命题 2 :相等的角是对顶角.
(2)判断这个命题的真假.
假命题
结论:
两个角相等.
这两个角互为对顶角.
你能否举例说明“相等的角是对顶角”是假命题?
如图,OC 是 ∠AOB 的平分线,∠1 = ∠2 ,但它们不是对顶角 .
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
知识归纳
1.命题的定义及构成:
表示判断性的语句叫命题,命题由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项;
命题通常写成“如果……那么……”的形式,“如果”后接的部分是题设,“那么”后接的部分是结论;
有些命题没有写成“如果……那么……”的形式,题设与结论不明显,这时要分清命题判断了什么事情,有什么已知事项,再改写成“如果……那么……”的形式.
命题的真假
命题分为真命题和假命题,如果题设成立,那么结论一定成立的命题叫做真命题.
如果题设成立,不能保证结论一定成立的命题叫做假命题.
定理及证明
定理是经过推理证实的真命题,是在今后推理中经常作为依据的一种真命题.但不是所有经过推理证实的真命题都把它当作定理;
在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程就叫证明.
例题与练习
例 指出下列命题的题设和结论:①如果两个数互为相反数,那么这两个数的和为0;②两直线平行,内错角相等;③等式的两边同乘以一个数,结果仍是等式;④绝对值相等的两个数相等;⑤如果AB⊥CD,垂足是O,那么∠AOC=90°.
解:①题设:两个数互为相反数;结论:这两个数的和为0;②题设:两直线平行;结论:内错角相等;③题设:等式两边同乘以一个数;结论:结果仍是等式;④题设:两个数的绝对值相等;结论:这两个数相等;⑤题设:AB⊥CD,垂足是O;结论:∠AOC=90°.
例 判断下列命题是真命题还是假命题.
(1)若a>b,则a2>b2;
(2)如果两个角互补,那么它们是邻补角;
(3)两点之间,线段最短; (4)任意两个直角都相等.
解:(1)(2)是假命题,(3)(4)是真命题.
2.判断一个命题的真假,只要举出一个______,它符合命题的______,但不满足结论就可以了.
思考
1.证明中的每一步推理都要有根据,不能“想当然”,这些根据,可以是________,也可以是学过的______、_________、_____等.
已知条件
定义
基本事实
定理
反例
题设
例题与练习
练习
1.下列语句中,是命题的是 ( )
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?
③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④ C.①②⑤ D.②③④⑤
A
2.下列命题中,是真命题的是( )
A.若|x|=2,则x=2
B.平行于同一条直线的两条直线平行
C.任何一个角都比它的补角小
D.一个锐角与一个钝角的和等于一个平角
B
证明:∵AD∥BE,
∴∠A=∠CBE.
∵∠1=∠2,
∴AC∥DE,
∴∠E=∠CBE,
∴∠A=∠E.
3.如图,已知AD∥BE,∠1=∠2.求证:∠A=∠E.
课堂小结
命题、定理、证明
定义
结构
形式
分类
真命题 定理
假命题举反例
题设:已知事项
结论:由已知事项推出的事项
:判断一件事情的语句叫做命题
:如果……那么……
证明
谢谢观看
人教版数学七年级下册
第五章 相交线与平行线
5.3 平行线的性质
5.3.1 平行线的性质
导入新课
回顾
窗户内窗的两条竖直的边是平行的,在推动过程中,两条竖直的边与窗户外框形成的两个角∠1,∠2有什么数量关系?
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
探究新知
知识点
平行线
两条平行线被第三条直线截得的同位角具有怎样的数量关系?
思考
如图,已知直线 a∥b ,c 是截线.
b
a
c
1
2
3
4
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
探究
∠1,∠2,···,∠8 中,哪些是同位角?它们的度数之间有什么关系?
由此猜想:
两条平行线被第三条直线截得的同位角有什么关系?
相等
b
a
c
1
2
3
4
5
6
7
8
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
b
a
c
1
2
3
4
5
6
7
8
d
成立
性质 1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
思考
如图,直线 a∥b ,c 是截线,那么 1 与 2 相等吗?为什么?
根据“两直线平行,同位角相等”,可得∠2 = ∠3 .
而∠3 与∠1 互为对顶角,所以∠3 =∠1.
所以∠1 = ∠2.
b
a
c
3
2
1
性质 2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
性质 3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
类似地,
知识归纳
平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
例题与练习
例1 如图,是一块梯形铁片的残余部分,量得∠A = 100 ° ,∠B = 115 ° ,梯形的另外两个角分别是多少度?
解:因为梯形上、下两底 AB∥CD ,根据“两直线平行,同旁内角互补”,可得∠A 与∠D 互补,∠B与∠C 互补.
于是∠D = 180 ° -∠A
= 180 ° -100 = 80 ° ,
∠C = 180 ° -∠B
= 180 ° -115 ° = 65 ° .
所以,梯形的另外两个角分别是 80 ° ,65°.
例2
如图,已知DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
解:∵FG∥EC,
∴∠CAG=∠ACE=36°,
∴∠PAC=∠CAG+∠PAG=36°+12°=48°.
∵AP平分∠BAC,
∴∠BAP=∠PAC=48°.
∵DB∥FG,
∴∠ABD=∠BAG=∠BAP+∠PAG=48°+12°=60°.
例3 如图,已知AB∥CD,直线EF分别交AB,CD于点M,N,MP平分∠EMA,NQ平分∠MNC,那么MP∥NQ,为什么?
解:∵AB∥CD,
∴∠EMA=∠MNC.
∵MP平分∠EMA,NQ平分∠MNC,∴∠EMP= ∠EMA,∠MNQ= ∠MNC,∴∠EMP=∠MNQ,∴MP∥NQ.
例题与练习
练习
1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4 各是多少度?
解:∵a∥b,∠1=54°,∴∠4 =∠1 = 54°(两直线平行,同位角相等).
∠3 =180°-∠4
=180° - 54°=126°,
∠2 与∠1 是对顶角,
∴∠2=∠1= 54°.
2. 如图,在△ABC 中,D 是 AB 上一点,E 是 AC 上一点, ∠ADE = 60°,∠B = 60°,∠AED = 40°.
(1)DE 与 BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
解:(1)∵∠ADE = ∠B,∴DE∥BC(同位角相等,两直线平行)
(2)∵DE∥BC,
∴∠C = ∠AED = 40°(两直线平行,同位角相等)
3.下列图形中,根据AB∥CD,能得到∠1=∠2的是( )
B
4.如图,若∠1+∠2=180°,∠3=110°,则∠4=_______.
110°
5.如图,CD⊥AB于点D,E是BC上一点,EF⊥AB于点F,∠1=∠2,试说明∠AGD=∠ACB的理由.
解:∵CD⊥AB,EF⊥AB,
∴∠EFB=∠CDB=90°,
∴CD∥EF,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴DG∥BC,∴∠AGD=∠ACB.
课堂小结
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
人教版数学七年级下册
第五章 相交线与平行线
5.3 平行线的性质
5.3.2 命题、定理、证明
导入新课
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
回顾
平行线的判定和性质
2.如图,直线a,b被直线c所截,则下列说法正确的是( )
思考完成并交流展示.
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠2-∠1=90°
D.当∠1+∠2=180°时,一定有a∥b
D
探究新知
知识点
命题
(1)如果两条直线都与第三条直线平行,那 么这两条直线也互相平行;
(2)两条平行线被第三条直线所截,同旁内 角互补;
(3)对顶角相等;
(4)等式两边都加同一个数,结果仍是等式.
像这样判断一件事情的语句,叫做命题(proposition).
思考
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
(2)两条平行线被第三条直线所截,同旁内角互补.
(3)如果两个角的和是 90 ,那么这两个角互余.
(4)等式两边都加同一个数, 结果仍是等式.
(5)两点之间,线段最短.
下列各组命题是由几部分组成的?
命题的结构
命题由题设和结论两部分组成.
许多数学命题常可以写成“如果……,那么……”的形式.“如果”后面连接的部分是题设,“那么”后面连接的部分是结论.
已知事项
由已知事项推出的事项
上面练习题中哪些命题是正确的,哪些命题是错误的?
(1)两条直线被第三条直线所截,同旁内角互补;
(2)等式两边都加同一个数,结果仍是等式;
(3)互为相反数的两个数相加得0;
(4)同旁内角互补;
(5)对顶角相等.
√
×
×
√
√
思考
命题的真假
真命题:
假命题:
如果题设成立,那么结论一定成立,这样的命题叫做真命题.
如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
练习
1. 指出下列命题的题设和结论:
(1)如果 AB⊥CD ,垂足为 O ,那么∠AOC = 90°.
题设:如果 AB⊥CD ,垂足为 O ,结论:∠AOC = 90°.
(2)如果∠1=∠2,∠2=∠3,那么∠1=∠3.
题设:如果∠1=∠2,∠2=∠3,结论:∠1=∠3.
题设:如果两条直线平行,结论:同位角相等.
(3)两直线平行,同位角相等.
2.判断下列命题哪些是真命题?哪些是假命题?
(1)在同一平面内,如果一条直线垂直于两 条平行线中的一条,那么也垂直于另一条;
(2)如果两个角互补,那么它们是邻补角;
(3)如果 | a | = | b |,那么 a = b ;
(4)经过直线外一点有且只有一条直线与这 条直线平行;
(5)两点确定一条直线.
真命题
假命题
假命题
真命题
真命题
知识点
定理与证明
上面练习第 2 题中的(1)(4)(5)它们的正确性是经过推理证实的,这样得到的真命题叫做定理(theorem).
定理也可以作为继续推理的依据.
在很多情况下,一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
命题 1 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
请判断下列两个命题的真假,并思考如何判断命题的真假.
命题 2 相等的角是对顶角.
题设:
命题 1:在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
(1)这个命题的题设和结论分别是什么呢?
结论:
在同一平面内,一条直线垂直于两条平行线中的一条;
这条直线也垂直于两条平行线中的另一条.
(2)命题 1 是真命题还是假命题?
真命题
命题 1:在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条.
(3)你能画出图形,写出已知、求证并证明它是真命题吗?
已知:b∥c, a⊥b .
求证:a⊥c.
b
c
a
证明:∵ a⊥b(已知),
∴∠1 = 90 (垂直的定义).
又∵ b∥c(已知),
∴∠1 = ∠2(两直线平行,同位角相等).
∴∠2 = ∠1 = 90 (等量代换).
∴ a⊥c(垂直的定义).
1
b
2
c
a
例 如图,已知:直线 b∥c,a⊥b. 求证:a⊥c.
归纳
证明中的每一步推理都要有根据,这些根据可以是已知条件,也可以是定义、基本事实、定理等.
题设:
(1)这个命题的题设和结论分别是什么呢?
命题 2 :相等的角是对顶角.
(2)判断这个命题的真假.
假命题
结论:
两个角相等.
这两个角互为对顶角.
你能否举例说明“相等的角是对顶角”是假命题?
如图,OC 是 ∠AOB 的平分线,∠1 = ∠2 ,但它们不是对顶角 .
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
知识归纳
1.命题的定义及构成:
表示判断性的语句叫命题,命题由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项;
命题通常写成“如果……那么……”的形式,“如果”后接的部分是题设,“那么”后接的部分是结论;
有些命题没有写成“如果……那么……”的形式,题设与结论不明显,这时要分清命题判断了什么事情,有什么已知事项,再改写成“如果……那么……”的形式.
命题的真假
命题分为真命题和假命题,如果题设成立,那么结论一定成立的命题叫做真命题.
如果题设成立,不能保证结论一定成立的命题叫做假命题.
定理及证明
定理是经过推理证实的真命题,是在今后推理中经常作为依据的一种真命题.但不是所有经过推理证实的真命题都把它当作定理;
在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程就叫证明.
例题与练习
例 指出下列命题的题设和结论:①如果两个数互为相反数,那么这两个数的和为0;②两直线平行,内错角相等;③等式的两边同乘以一个数,结果仍是等式;④绝对值相等的两个数相等;⑤如果AB⊥CD,垂足是O,那么∠AOC=90°.
解:①题设:两个数互为相反数;结论:这两个数的和为0;②题设:两直线平行;结论:内错角相等;③题设:等式两边同乘以一个数;结论:结果仍是等式;④题设:两个数的绝对值相等;结论:这两个数相等;⑤题设:AB⊥CD,垂足是O;结论:∠AOC=90°.
例 判断下列命题是真命题还是假命题.
(1)若a>b,则a2>b2;
(2)如果两个角互补,那么它们是邻补角;
(3)两点之间,线段最短; (4)任意两个直角都相等.
解:(1)(2)是假命题,(3)(4)是真命题.
2.判断一个命题的真假,只要举出一个______,它符合命题的______,但不满足结论就可以了.
思考
1.证明中的每一步推理都要有根据,不能“想当然”,这些根据,可以是________,也可以是学过的______、_________、_____等.
已知条件
定义
基本事实
定理
反例
题设
例题与练习
练习
1.下列语句中,是命题的是 ( )
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?
③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④ C.①②⑤ D.②③④⑤
A
2.下列命题中,是真命题的是( )
A.若|x|=2,则x=2
B.平行于同一条直线的两条直线平行
C.任何一个角都比它的补角小
D.一个锐角与一个钝角的和等于一个平角
B
证明:∵AD∥BE,
∴∠A=∠CBE.
∵∠1=∠2,
∴AC∥DE,
∴∠E=∠CBE,
∴∠A=∠E.
3.如图,已知AD∥BE,∠1=∠2.求证:∠A=∠E.
课堂小结
命题、定理、证明
定义
结构
形式
分类
真命题 定理
假命题举反例
题设:已知事项
结论:由已知事项推出的事项
:判断一件事情的语句叫做命题
:如果……那么……
证明
谢谢观看
