物理人教版(2019)选择性必修第一册2.1简谐运动(共15张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册2.1简谐运动(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 27.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-02-22 15:44:56 | ||
图片预览






文档简介
(共15张PPT)
第二章 机械振动
选择性必修一
2.1 简谐振动
【总结】物体在某位置附近做往复的周期性运动
单摆来回摆动 物体上下摆动 琴弦的抖动
观察以下运动,这些运动的共同特点是什么?
机械振动:物体或物体的一部分在一个位置附近的往复运动,简称振动。
高中阶段我们学过的运动形式有哪些?
按加速度分类:
a=0 :匀速直线运动
且与初速度方向在同一直线:匀变速直线运动
a大小不变、方向改变:匀速圆周运动
a恒定:
且与初速度方向不在同一直线:抛体运动
a变化:
a大小、方向均改变:机械振动
1.定义:物体或物体的一部分在一个位置附近的往复运动叫做机械振动,
简称振动。
3.特点:
(1)具有一个平衡位置;
(2)具有对称性、周期性;
(3)具有一个使它回到平衡位置的力。
一、机械振动
平衡位置
2.平衡位置:振子原来静止时的位置。(合力为0)
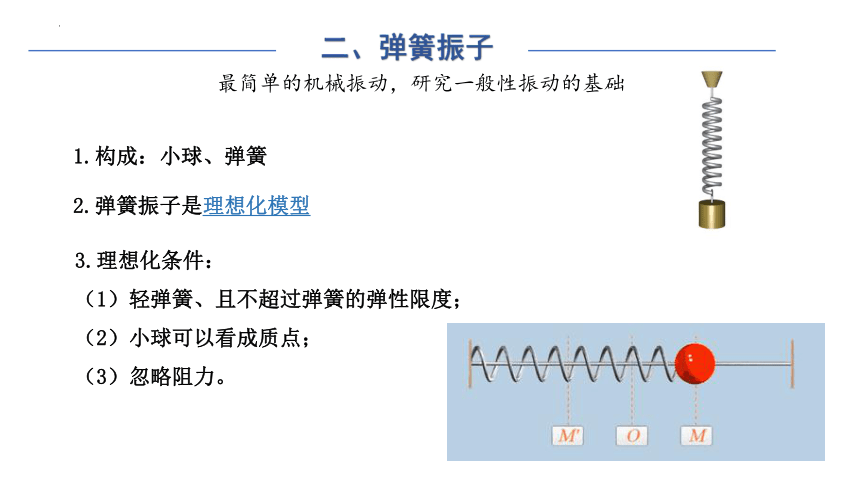
1.构成:小球、弹簧
3.理想化条件:
(1)轻弹簧、且不超过弹簧的弹性限度;
(2)小球可以看成质点;
(3)忽略阻力。
二、弹簧振子
2.弹簧振子是理想化模型
最简单的机械振动,研究一般性振动的基础
1.振子的位移:从平衡位置指向小球所在位置的有向线段
三、弹簧振子的位移——时间图像
x1
x2
弹簧振子
注意:振子位移和机械运动的位移定义上的区别
2.弹簧振子的位移——时间图像:
三、弹簧振子的位移——时间图像
①建立坐标系:
以小球的平衡位置为坐标原点0
沿着弹簧振子的振动方向建立纵轴
垂直于弹簧振子振动方向建立横轴
②标出各时刻小球球心的位置坐标;
③用曲线把各点连接起来。
以上实验中画出的小球运动的x—t图象很像正弦曲线,是不是这样呢?如何验证?
方法一:正弦函数代入法
方法二:计算机函数图像耦合法
思考:简谐运动的位移-时间(x-t)图像是不是质点的轨迹?
四、简谐振动
1.定义:如果物体的位移与时间的关系遵从正弦函数的规律,即它的振动图
像(x-t图像)是一条正弦曲线,这样的振动是一种简谐运动。
简谐运动是最基本的振动。
3.图象意义:表示一个振子不同时刻所在的位置或者一个振子位移随时间的
变化规律。
2.运动性质:非匀变速运动
四、简谐振动
4.从图像获取信息
①任意时刻质点的位移的大小和方向;
②任意时刻质点的振动方向;
③任意时刻质点的速度、加速度、位移的变化情况;
回答:a、b、c三点的位移、速度如何?
思考:图像的斜率代表什么含义?
四、简谐振动
位置 O→M M O→M’ O O→M’ M’ M’ →O
位移 增大、向右 最大 减小、向右 0 增大、向左 最大 减小、向左
速度 减小、向右 0 增大、向左 最大 减小、向左 0 增大、向右
加速度 增大、向左 最大 减小、向左 0 增大、向右 最大 减小、向右
四、简谐振动
1.位移与速度的关系:一增一减、有时同向、有时反向
2.位移与加速度的关系:同增同减、始终反向
最大位移处,速度方向改变;
平衡位置处,速度最大。
【总结】
第二章 机械振动
选择性必修一
2.1 简谐振动
【总结】物体在某位置附近做往复的周期性运动
单摆来回摆动 物体上下摆动 琴弦的抖动
观察以下运动,这些运动的共同特点是什么?
机械振动:物体或物体的一部分在一个位置附近的往复运动,简称振动。
高中阶段我们学过的运动形式有哪些?
按加速度分类:
a=0 :匀速直线运动
且与初速度方向在同一直线:匀变速直线运动
a大小不变、方向改变:匀速圆周运动
a恒定:
且与初速度方向不在同一直线:抛体运动
a变化:
a大小、方向均改变:机械振动
1.定义:物体或物体的一部分在一个位置附近的往复运动叫做机械振动,
简称振动。
3.特点:
(1)具有一个平衡位置;
(2)具有对称性、周期性;
(3)具有一个使它回到平衡位置的力。
一、机械振动
平衡位置
2.平衡位置:振子原来静止时的位置。(合力为0)
1.构成:小球、弹簧
3.理想化条件:
(1)轻弹簧、且不超过弹簧的弹性限度;
(2)小球可以看成质点;
(3)忽略阻力。
二、弹簧振子
2.弹簧振子是理想化模型
最简单的机械振动,研究一般性振动的基础
1.振子的位移:从平衡位置指向小球所在位置的有向线段
三、弹簧振子的位移——时间图像
x1
x2
弹簧振子
注意:振子位移和机械运动的位移定义上的区别
2.弹簧振子的位移——时间图像:
三、弹簧振子的位移——时间图像
①建立坐标系:
以小球的平衡位置为坐标原点0
沿着弹簧振子的振动方向建立纵轴
垂直于弹簧振子振动方向建立横轴
②标出各时刻小球球心的位置坐标;
③用曲线把各点连接起来。
以上实验中画出的小球运动的x—t图象很像正弦曲线,是不是这样呢?如何验证?
方法一:正弦函数代入法
方法二:计算机函数图像耦合法
思考:简谐运动的位移-时间(x-t)图像是不是质点的轨迹?
四、简谐振动
1.定义:如果物体的位移与时间的关系遵从正弦函数的规律,即它的振动图
像(x-t图像)是一条正弦曲线,这样的振动是一种简谐运动。
简谐运动是最基本的振动。
3.图象意义:表示一个振子不同时刻所在的位置或者一个振子位移随时间的
变化规律。
2.运动性质:非匀变速运动
四、简谐振动
4.从图像获取信息
①任意时刻质点的位移的大小和方向;
②任意时刻质点的振动方向;
③任意时刻质点的速度、加速度、位移的变化情况;
回答:a、b、c三点的位移、速度如何?
思考:图像的斜率代表什么含义?
四、简谐振动
位置 O→M M O→M’ O O→M’ M’ M’ →O
位移 增大、向右 最大 减小、向右 0 增大、向左 最大 减小、向左
速度 减小、向右 0 增大、向左 最大 减小、向左 0 增大、向右
加速度 增大、向左 最大 减小、向左 0 增大、向右 最大 减小、向右
四、简谐振动
1.位移与速度的关系:一增一减、有时同向、有时反向
2.位移与加速度的关系:同增同减、始终反向
最大位移处,速度方向改变;
平衡位置处,速度最大。
【总结】
