19.1.1 变量与函数 课件(共43张PPT)
文档属性
| 名称 | 19.1.1 变量与函数 课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览











文档简介
(共43张PPT)
人教版数学八年级下册
第十九章 一次函数
19.1 函数
19.1.1 变量与函数
第1课时 变量与常量
导入新课
数学上常用常量与变量来刻画各种运动变化
大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢?
探究新知
思考
1.汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为 t 小时,填写下表,s的值随t的值的变化而变化吗?
t/h 1 2 3 4 5
s/km
60
120
180
240
300
请说明你的道理:
速度×时间
路程 =____________
(1)在以上这个过程中,变化的量是________________.不变化的量是_____________.
(2)试用含t的式子表示s.s=____.
时间t、
速度60千米/时
60 t
这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程.
路程s
s
t
2.每张电影票的售价为10元,如果早场售出票150张,日场售出205张,晚场售出310张,三场电影票的票房收入各多少元?若设一场电影售出票 x 张,票房收入为 y 元,y的值随x的值的变化而变化吗?
(1)早场票房收入 =
日场票房收入 =
晚场票房收入 =
请说明道理:
票房收入=
10×205 = 2050 (元)
10×150 = 1500(元)
10×310 = 3100 (元)
售价×售票张数
10x
(2)在以上这个过程中,变化的量是________________________.不变化的量是_________.
(2)试用含x的式子表示y,y=______.
售票张数x、票房收入y
售价10元
这个问题反映了票房收入____随售票张数_____的变化过程.
y
x
圆面积S与圆的半径R之间的关系式是 ;
其中变化的量是 ;不变化的量是 .
3.如图所示,圆形水波慢慢地扩大,在这一过程中,当圆的半径 r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别为多少?S的值随r的变化而变化吗
S= πr2
π
S,r
这个问题反映了圆的面积S随半径R的变化过程.
S1=π102
S2=π202
S3=π302
4.用10m长的绳子围一个矩形.当矩形的一边长x分别为3m,3.5m,4m,4.5m时,它的邻边长y分别为多少?y的值随x的值变化而变化吗
请说明你的道理:
矩形周长=____________
2(x+y)
当x=3m,y=10÷2-3=2m
当x=3.5m,y=10÷2-3.5=1.5m
当x=4m,y=10÷2-4=1m
当x=4.5m,y=10÷2-4.5=0.5m
这个问题反映了矩形的邻边长y随边长x的变化而变化.
知识归纳
上述运动变化过程中出现的数量,你发现了什么?
有些量的数值是变化的,例如时间t,路程s,售出票数x……
有些量的数值是始终不变的,例如速度60km/h,票价10元/张……
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
练习
1.某市的自来水价为4元/t.现要抽取若干户居民调查水费支出情况,记某户月用水量为x t,月应交水费y元.
变量:月用水量x t,月应交水费y元;
常量:自来水价4元/t.
指出下列问题中的变量和常量:
2.某地手机通话费为0.2元/min.李明在手机话费卡中存入30元,记此后他的手机通话时间为 t min,话费卡中的余额为w元.
变量:通话时间 t min,话费卡中的余额w元;
常量:通话费0.2元/min.
3.水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率(圆周长和直径之比)为π.
变量:半径r,圆周长C;
常量:圆周率π.
4.把10本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本.
变量:第一个抽屉x本,第二个抽屉y本;
常量:10本书.
探究新知
思考
问题1 ~ 4中是否各有两个变量?同一个问题中的变量之间有什么联系?
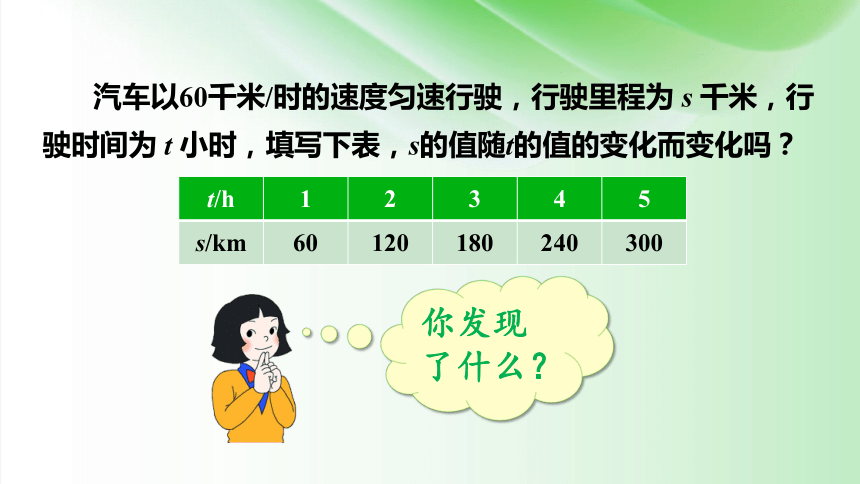
汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为 t 小时,填写下表,s的值随t的值的变化而变化吗?
t/h 1 2 3 4 5
s/km 60 120 180 240 300
你发现了什么?
知识归纳
四个问题中每个问题的两个变量相互联系,当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
例题与练习
(1)球的表面积S(cm2)与球的半径R(cm)的关系式是S=4πR2;
(2)一物体自高处自由落下,这个物体运动的距离h(m)与它下落的时间t(s)之间的关系式是h= gt2(其中g取9.8 m/s2 );
(3)已知橙子1.8 元/kg,则购买数量x(kg)与所付款w(元)之间的关系式是w=1.8x.
解:(1)S=4πR2,常量是4,π,变量是S,R;
(2)h= gt2,常量是 ,g,变量是h,t;
(3)w=1.8x,常量是1.8,变量是w,x.
例1 分析下列关系中的变量与常量.
例2 观察图表,根据表格中的数据回答问题:
梯形个数 1 2 3 4 5 …
图形周长 5 8 11 14 17 …
(1)设图形的周长为l,梯形的个数为n,试写出l与n的关系式;
(2)在上述变化过程中,常量、变量分别是什么?
(3)求n=11时图形的周长.
解:(1)l=3n+2;
(2)常量是3,2,变量是l,n;
(3)当n=11时,l=3×11+2=35,即此时图形的周长为35.
例题与练习
练习
1.下表是某报纸公布的世界人口数据情况,表中的变量( )
年份 1957 1974 1987 1999 2010
人口数 30亿 40亿 50亿 60亿 70亿
A.仅有一个,是年份
B.仅有一个,是人口数
C.有两个,一个是人口数,另一个是年份
D.一个也没有
C
2.张老师带领x名学生到某动物园参观,已知成人票每张10元,学生票每张5元,设门票的总费用为y元,则y=____________,其中_________是常量,_________是变量.
10+5x
10,5
y,x
3.写出下列问题中的关系式,并指出其中的变量和常量.
(1)直角三角形中一个锐角α与另一个锐角β之间的关系;
(2)甲、乙两地相距 ykm,小明骑自行车以每小时30 km的速度从甲地驶向乙地,试用行驶时间t(h)表示小明离乙地的距离s(km).
解:(1)α=90°-β,α和 β是变量,90°是常量;
(2)s=y-30t,s和t是变量,y和-30是常量.
课堂小结
常量与变量
常量与变量的概念
列出变量之间的关系式
常量:数值始终不变的量
变量:数值发生变化的量
人教版数学八年级下册
第十九章 一次函数
19.1 函数
19.1.1 变量与函数
第2课时 函数
导入新课
1.圆柱的体积公式V=πr2h,V表示体积,r表示底面的半径,h表示圆柱的高,其中常量是_____,变量是____________.
π
V,r,h
2.如图,水滴激起的波纹可以看成是一个不断向外扩展的圆,它的面积随着半径的变化而变化,随着半径的确定而确定.
在上述例子中,每个变化过程中的两个变量,当其中一个变量变化时,另一个变量也随之发生变化;当一个变量确定时,另一个变量也随之确定.
探究新知
思考
1.下图是体检时的心电图,图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的值与其对应吗?
2.下表是我国人口数统计表,年份与人口数可以分别记作两个变量x和y.对于表中每一个确定的年份x,都对应着一个确定的人口数y吗?
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
思考上面两个问题,你学到了什么?
1中每个时间x都对应一个生物电流y;
2中每个年份都对应一个确定的人口数.
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
知识归纳
你能从上述问题中得到什么结论吗?
指出下列问题中的自变量以及自变量的函数:
1.汽车以60km/h的速度匀速行驶,行驶路程为skm,行驶时间为th.
2.在我国人口数统计表,年份与人口数可以分别记作两个变量x和y.
t是自变量,s是t的函数.
x是自变量,y是x的函数.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
什么是函数值?
中国人口数统计表
你发现了什么?
每个年份对应一个人口数
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
探究新知
例 1 汽车油箱中有汽油50L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1L/km.
油箱中的剩油量、汽车耗油量与油箱中原有油量之间有怎样的数量关系?
(1)写出表示y与x的函数关系的式子;
解:行驶路程x是自变量,油箱中的油量y是x的函数,它们的关系为:
y=50-0.1x
像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,这种式子叫做函数的解析式.
0.1x表示的意义是什么?
0.1x表示行驶过程中消耗的总油量.
(2)指出自变量x的取值范围;
确定自变量的取值范围时,不仅要考虑使函数解析式有意义,而且还要注意各变量所代表的实际意义.
归纳
解析:仅从式子y=50-0.1x看,x可以取任意实数.但是考虑到x代表的实际意义为行驶路程,因此x不能取负数.行驶中的耗油量为0.1x,它不能超过邮箱中现有油量50,即:0.1x≤50.
因此,自变量x的取值范围是0≤x≤500.
像这样,使函数有意义的自变量的取值叫做自变量的取值范围.
(3)汽车行驶200 km时,油箱中还有多少油?
解析:汽车行驶200km时,油箱中的汽油量是函数y=50-0.1x在x=200时的函数值.将x=200带入y=50-0.1x,得:
y=50-0.1×200=30
答:汽车行驶200km时,油箱中还有30L汽油.
练习
1.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出函数的解析式.
(1)改变正方形的边长x,正方形的面积S随之改变.
S=x2
自变量
自变量的函数
(2)每分钟向一水池注水0.1m3,注水量y(单位:m3)随注水时间x(单位:min)的变化而变化.
y=0.1x
自变量
自变量的函数
(3)秀水村的耕地面积是106m2,这个村人均占有耕地面积y(单位:m2)随这个村人数n的变化而变化.
自变量
自变量的函数
(4)水池中有水10L,此后每小时漏水0.05L,水池中的水量V(单位:L)随时间t(单位:h)的变化而变化.
V=10-0.05t
自变量
自变量的函数
2.梯形的上底长2cm,高3cm,下底长xcm大于上底长,但不超过5cm.写出梯形面积S关于x的函数解析式及自变量x的取值范围.
2<x≤5
S= (2+x) ×3;
例题与练习
例2 下列问题中哪些量是自变量?哪些量是自变量的函数?试写出用自变量表示函数的式子.
(1)一个弹簧秤最大能称不超过10 kg的物体,它的原长为10 cm,挂上重物后弹簧的长度y(cm)随所挂重物的质量x(kg)的变化而变化,每挂1 kg物体,弹簧伸长0.5 cm;
解:(1)y=10+ x,其中x是自变量,y是自变量的函数;
(2)V=30a2,其中a是自变量,V是自变量的函数.
例2 下列问题中哪些量是自变量?哪些量是自变量的函数?试写出用自变量表示函数的式子.
(2)设一长方体盒子的高为30 cm,底面是正方形,底面边长a(cm)改变时,这个长方体的体积V(cm3)也随之改变.
例3 求下列自变量的取值范围.
解:x为全体实数
解得x≥1;
解:2x-1>0,
例4 水箱内原有水200 L,7:30打开水龙头,以2 L/min的速度放水,设经t min时,水箱内存水y L.
(1)求y与t的函数关系式和自变量的取值范围;
解:(1)∵水箱内存有的水=原有水-放掉的水,
∴y=200-2t.
∵y≥0,
∴200-2t≥0,解得t≤100.
∴0≤t≤100;
(2)∵7:55-7:30=25(min),
∴当t=25时,y=200-2t=200-50=150.
∴当7:55时,水箱内还有水150 L;
(3)当y=0时,200-2t=0,解得t=100,而100分=1小时40分,7点30分+1小时40分=9点10分,故9点10分水箱内的水恰好放完.
例4 水箱内原有水200 L,7:30打开水龙头,以2 L/min的速度放水,设经t min时,水箱内存水y L.
(2)7:55时,水箱内还有多少水?
(3)几点几分水箱内的水恰好放完?
例题与练习
练习
1.下列各关系式中,y不是x的函数的是( )
A.y=3-2x B.y=x2-5 C.y=9x D.y2=x+6
D
2.如图,当输入x=-1时,输出y=________.
-5
3.已知水池中有800 m3的水,每小时抽50 m3.
(1)写出剩余水的体积Q(m3)与时间t(h)之间的函数解析式;
(2)写出自变量t的取值范围;
(3)10 h后,池中还有多少水?
解:(1)Q=800-50t;
(2)∵Q≥0,
∴800-50t≥0,
∴0≤t≤16;
(3)当t=10时,
Q=800-50×10=300.
答:10 h后,池中还有300 m3水.
课堂小结
函数
函数及自变量的概念
函数值
自变量的取值范围
使函数解析式有意义
符合实际意义
谢谢观看
人教版数学八年级下册
第十九章 一次函数
19.1 函数
19.1.1 变量与函数
第1课时 变量与常量
导入新课
数学上常用常量与变量来刻画各种运动变化
大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢?
探究新知
思考
1.汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为 t 小时,填写下表,s的值随t的值的变化而变化吗?
t/h 1 2 3 4 5
s/km
60
120
180
240
300
请说明你的道理:
速度×时间
路程 =____________
(1)在以上这个过程中,变化的量是________________.不变化的量是_____________.
(2)试用含t的式子表示s.s=____.
时间t、
速度60千米/时
60 t
这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程.
路程s
s
t
2.每张电影票的售价为10元,如果早场售出票150张,日场售出205张,晚场售出310张,三场电影票的票房收入各多少元?若设一场电影售出票 x 张,票房收入为 y 元,y的值随x的值的变化而变化吗?
(1)早场票房收入 =
日场票房收入 =
晚场票房收入 =
请说明道理:
票房收入=
10×205 = 2050 (元)
10×150 = 1500(元)
10×310 = 3100 (元)
售价×售票张数
10x
(2)在以上这个过程中,变化的量是________________________.不变化的量是_________.
(2)试用含x的式子表示y,y=______.
售票张数x、票房收入y
售价10元
这个问题反映了票房收入____随售票张数_____的变化过程.
y
x
圆面积S与圆的半径R之间的关系式是 ;
其中变化的量是 ;不变化的量是 .
3.如图所示,圆形水波慢慢地扩大,在这一过程中,当圆的半径 r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别为多少?S的值随r的变化而变化吗
S= πr2
π
S,r
这个问题反映了圆的面积S随半径R的变化过程.
S1=π102
S2=π202
S3=π302
4.用10m长的绳子围一个矩形.当矩形的一边长x分别为3m,3.5m,4m,4.5m时,它的邻边长y分别为多少?y的值随x的值变化而变化吗
请说明你的道理:
矩形周长=____________
2(x+y)
当x=3m,y=10÷2-3=2m
当x=3.5m,y=10÷2-3.5=1.5m
当x=4m,y=10÷2-4=1m
当x=4.5m,y=10÷2-4.5=0.5m
这个问题反映了矩形的邻边长y随边长x的变化而变化.
知识归纳
上述运动变化过程中出现的数量,你发现了什么?
有些量的数值是变化的,例如时间t,路程s,售出票数x……
有些量的数值是始终不变的,例如速度60km/h,票价10元/张……
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
练习
1.某市的自来水价为4元/t.现要抽取若干户居民调查水费支出情况,记某户月用水量为x t,月应交水费y元.
变量:月用水量x t,月应交水费y元;
常量:自来水价4元/t.
指出下列问题中的变量和常量:
2.某地手机通话费为0.2元/min.李明在手机话费卡中存入30元,记此后他的手机通话时间为 t min,话费卡中的余额为w元.
变量:通话时间 t min,话费卡中的余额w元;
常量:通话费0.2元/min.
3.水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率(圆周长和直径之比)为π.
变量:半径r,圆周长C;
常量:圆周率π.
4.把10本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本.
变量:第一个抽屉x本,第二个抽屉y本;
常量:10本书.
探究新知
思考
问题1 ~ 4中是否各有两个变量?同一个问题中的变量之间有什么联系?
汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为 t 小时,填写下表,s的值随t的值的变化而变化吗?
t/h 1 2 3 4 5
s/km 60 120 180 240 300
你发现了什么?
知识归纳
四个问题中每个问题的两个变量相互联系,当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
例题与练习
(1)球的表面积S(cm2)与球的半径R(cm)的关系式是S=4πR2;
(2)一物体自高处自由落下,这个物体运动的距离h(m)与它下落的时间t(s)之间的关系式是h= gt2(其中g取9.8 m/s2 );
(3)已知橙子1.8 元/kg,则购买数量x(kg)与所付款w(元)之间的关系式是w=1.8x.
解:(1)S=4πR2,常量是4,π,变量是S,R;
(2)h= gt2,常量是 ,g,变量是h,t;
(3)w=1.8x,常量是1.8,变量是w,x.
例1 分析下列关系中的变量与常量.
例2 观察图表,根据表格中的数据回答问题:
梯形个数 1 2 3 4 5 …
图形周长 5 8 11 14 17 …
(1)设图形的周长为l,梯形的个数为n,试写出l与n的关系式;
(2)在上述变化过程中,常量、变量分别是什么?
(3)求n=11时图形的周长.
解:(1)l=3n+2;
(2)常量是3,2,变量是l,n;
(3)当n=11时,l=3×11+2=35,即此时图形的周长为35.
例题与练习
练习
1.下表是某报纸公布的世界人口数据情况,表中的变量( )
年份 1957 1974 1987 1999 2010
人口数 30亿 40亿 50亿 60亿 70亿
A.仅有一个,是年份
B.仅有一个,是人口数
C.有两个,一个是人口数,另一个是年份
D.一个也没有
C
2.张老师带领x名学生到某动物园参观,已知成人票每张10元,学生票每张5元,设门票的总费用为y元,则y=____________,其中_________是常量,_________是变量.
10+5x
10,5
y,x
3.写出下列问题中的关系式,并指出其中的变量和常量.
(1)直角三角形中一个锐角α与另一个锐角β之间的关系;
(2)甲、乙两地相距 ykm,小明骑自行车以每小时30 km的速度从甲地驶向乙地,试用行驶时间t(h)表示小明离乙地的距离s(km).
解:(1)α=90°-β,α和 β是变量,90°是常量;
(2)s=y-30t,s和t是变量,y和-30是常量.
课堂小结
常量与变量
常量与变量的概念
列出变量之间的关系式
常量:数值始终不变的量
变量:数值发生变化的量
人教版数学八年级下册
第十九章 一次函数
19.1 函数
19.1.1 变量与函数
第2课时 函数
导入新课
1.圆柱的体积公式V=πr2h,V表示体积,r表示底面的半径,h表示圆柱的高,其中常量是_____,变量是____________.
π
V,r,h
2.如图,水滴激起的波纹可以看成是一个不断向外扩展的圆,它的面积随着半径的变化而变化,随着半径的确定而确定.
在上述例子中,每个变化过程中的两个变量,当其中一个变量变化时,另一个变量也随之发生变化;当一个变量确定时,另一个变量也随之确定.
探究新知
思考
1.下图是体检时的心电图,图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的值与其对应吗?
2.下表是我国人口数统计表,年份与人口数可以分别记作两个变量x和y.对于表中每一个确定的年份x,都对应着一个确定的人口数y吗?
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
思考上面两个问题,你学到了什么?
1中每个时间x都对应一个生物电流y;
2中每个年份都对应一个确定的人口数.
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
知识归纳
你能从上述问题中得到什么结论吗?
指出下列问题中的自变量以及自变量的函数:
1.汽车以60km/h的速度匀速行驶,行驶路程为skm,行驶时间为th.
2.在我国人口数统计表,年份与人口数可以分别记作两个变量x和y.
t是自变量,s是t的函数.
x是自变量,y是x的函数.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
什么是函数值?
中国人口数统计表
你发现了什么?
每个年份对应一个人口数
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
探究新知
例 1 汽车油箱中有汽油50L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1L/km.
油箱中的剩油量、汽车耗油量与油箱中原有油量之间有怎样的数量关系?
(1)写出表示y与x的函数关系的式子;
解:行驶路程x是自变量,油箱中的油量y是x的函数,它们的关系为:
y=50-0.1x
像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,这种式子叫做函数的解析式.
0.1x表示的意义是什么?
0.1x表示行驶过程中消耗的总油量.
(2)指出自变量x的取值范围;
确定自变量的取值范围时,不仅要考虑使函数解析式有意义,而且还要注意各变量所代表的实际意义.
归纳
解析:仅从式子y=50-0.1x看,x可以取任意实数.但是考虑到x代表的实际意义为行驶路程,因此x不能取负数.行驶中的耗油量为0.1x,它不能超过邮箱中现有油量50,即:0.1x≤50.
因此,自变量x的取值范围是0≤x≤500.
像这样,使函数有意义的自变量的取值叫做自变量的取值范围.
(3)汽车行驶200 km时,油箱中还有多少油?
解析:汽车行驶200km时,油箱中的汽油量是函数y=50-0.1x在x=200时的函数值.将x=200带入y=50-0.1x,得:
y=50-0.1×200=30
答:汽车行驶200km时,油箱中还有30L汽油.
练习
1.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出函数的解析式.
(1)改变正方形的边长x,正方形的面积S随之改变.
S=x2
自变量
自变量的函数
(2)每分钟向一水池注水0.1m3,注水量y(单位:m3)随注水时间x(单位:min)的变化而变化.
y=0.1x
自变量
自变量的函数
(3)秀水村的耕地面积是106m2,这个村人均占有耕地面积y(单位:m2)随这个村人数n的变化而变化.
自变量
自变量的函数
(4)水池中有水10L,此后每小时漏水0.05L,水池中的水量V(单位:L)随时间t(单位:h)的变化而变化.
V=10-0.05t
自变量
自变量的函数
2.梯形的上底长2cm,高3cm,下底长xcm大于上底长,但不超过5cm.写出梯形面积S关于x的函数解析式及自变量x的取值范围.
2<x≤5
S= (2+x) ×3;
例题与练习
例2 下列问题中哪些量是自变量?哪些量是自变量的函数?试写出用自变量表示函数的式子.
(1)一个弹簧秤最大能称不超过10 kg的物体,它的原长为10 cm,挂上重物后弹簧的长度y(cm)随所挂重物的质量x(kg)的变化而变化,每挂1 kg物体,弹簧伸长0.5 cm;
解:(1)y=10+ x,其中x是自变量,y是自变量的函数;
(2)V=30a2,其中a是自变量,V是自变量的函数.
例2 下列问题中哪些量是自变量?哪些量是自变量的函数?试写出用自变量表示函数的式子.
(2)设一长方体盒子的高为30 cm,底面是正方形,底面边长a(cm)改变时,这个长方体的体积V(cm3)也随之改变.
例3 求下列自变量的取值范围.
解:x为全体实数
解得x≥1;
解:2x-1>0,
例4 水箱内原有水200 L,7:30打开水龙头,以2 L/min的速度放水,设经t min时,水箱内存水y L.
(1)求y与t的函数关系式和自变量的取值范围;
解:(1)∵水箱内存有的水=原有水-放掉的水,
∴y=200-2t.
∵y≥0,
∴200-2t≥0,解得t≤100.
∴0≤t≤100;
(2)∵7:55-7:30=25(min),
∴当t=25时,y=200-2t=200-50=150.
∴当7:55时,水箱内还有水150 L;
(3)当y=0时,200-2t=0,解得t=100,而100分=1小时40分,7点30分+1小时40分=9点10分,故9点10分水箱内的水恰好放完.
例4 水箱内原有水200 L,7:30打开水龙头,以2 L/min的速度放水,设经t min时,水箱内存水y L.
(2)7:55时,水箱内还有多少水?
(3)几点几分水箱内的水恰好放完?
例题与练习
练习
1.下列各关系式中,y不是x的函数的是( )
A.y=3-2x B.y=x2-5 C.y=9x D.y2=x+6
D
2.如图,当输入x=-1时,输出y=________.
-5
3.已知水池中有800 m3的水,每小时抽50 m3.
(1)写出剩余水的体积Q(m3)与时间t(h)之间的函数解析式;
(2)写出自变量t的取值范围;
(3)10 h后,池中还有多少水?
解:(1)Q=800-50t;
(2)∵Q≥0,
∴800-50t≥0,
∴0≤t≤16;
(3)当t=10时,
Q=800-50×10=300.
答:10 h后,池中还有300 m3水.
课堂小结
函数
函数及自变量的概念
函数值
自变量的取值范围
使函数解析式有意义
符合实际意义
谢谢观看
