人教版八年级上册11.3.2 多边形的内角和课件(共15张PPT)
文档属性
| 名称 | 人教版八年级上册11.3.2 多边形的内角和课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 405.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 14:17:30 | ||
图片预览

文档简介
(共15张PPT)
11.3.2多边形的内角和
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
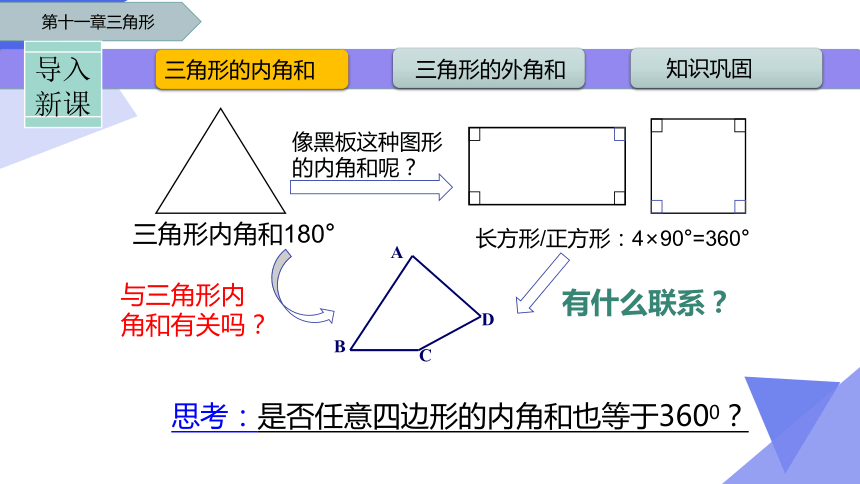
导入新课
思考:是否任意四边形的内角和也等于3600?
A
B
C
D
三角形内角和180°
长方形/正方形:4×90°=360°
与三角形内角和有关吗?
有什么联系?
像黑板这种图形的内角和呢?
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
A
B
C
D
A
B
C
D
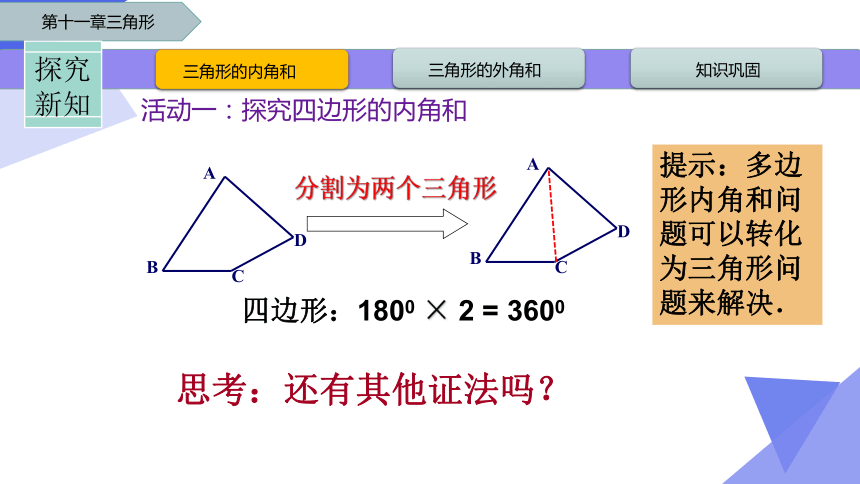
活动一:探究四边形的内角和
四边形:1800 × 2 = 3600
分割为两个三角形
提示:多边形内角和问题可以转化为三角形问题来解决.
思考:还有其他证法吗?
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
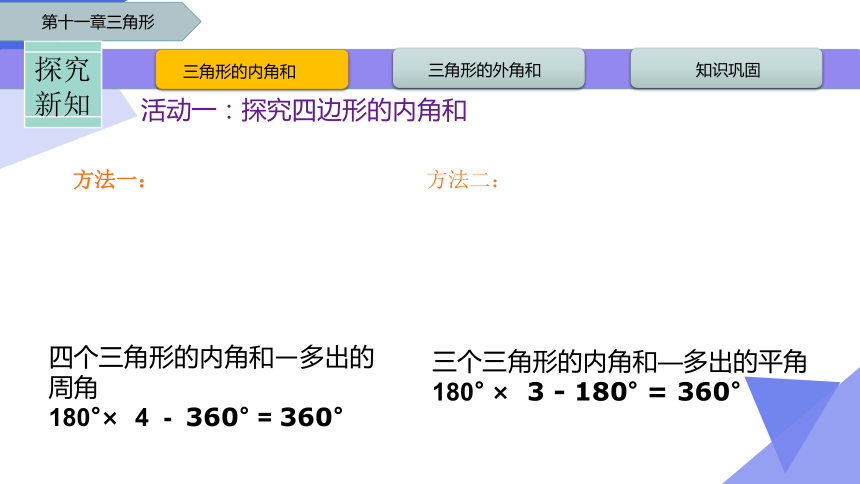
活动一:探究四边形的内角和
四个三角形的内角和—多出的周角
180°× 4 - 360° = 360°
三个三角形的内角和—多出的平角
180° × 3 - 180° = 360°
方法一:
方法二:
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
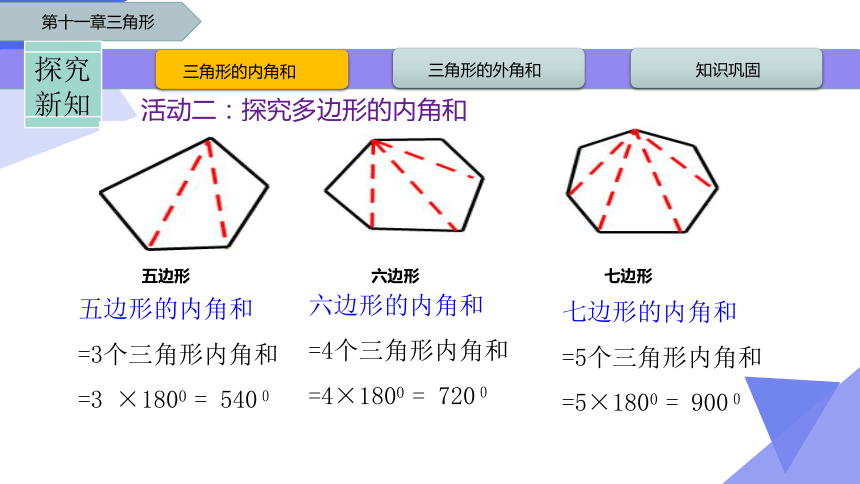
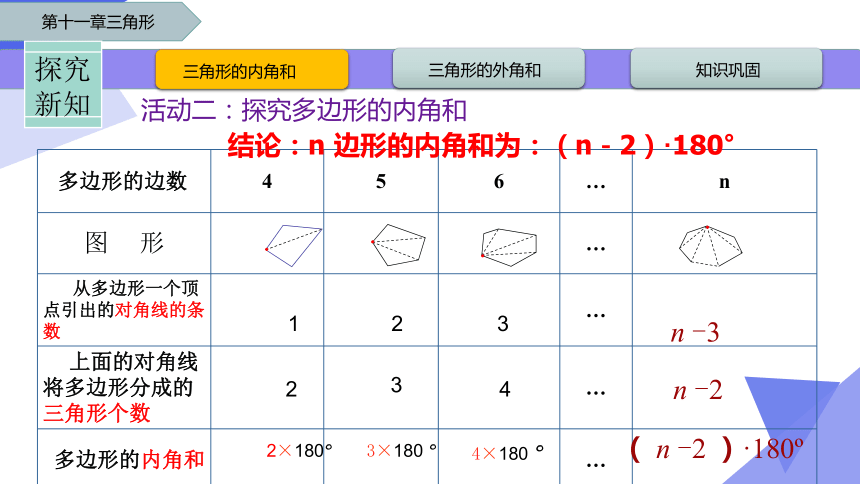
活动二:探究多边形的内角和
五边形
六边形
七边形
五边形的内角和
=3个三角形内角和
=3 ×1800 = 5400
六边形的内角和
=4个三角形内角和
=4×1800 = 7200
七边形的内角和
=5个三角形内角和
=5×1800 = 9000
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
活动二:探究多边形的内角和
多边形的边数 4 5 6 … n
图 形 …
从多边形一个顶点引出的对角线的条数 …
上面的对角线将多边形分成的三角形个数 …
多边形的内角和 …
4×180 °
3×180 °
2×180°
结论:n 边形的内角和为:(n-2)·180°
n -3
n -2
( n -2 )·180
1
2
3
2
3
4
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
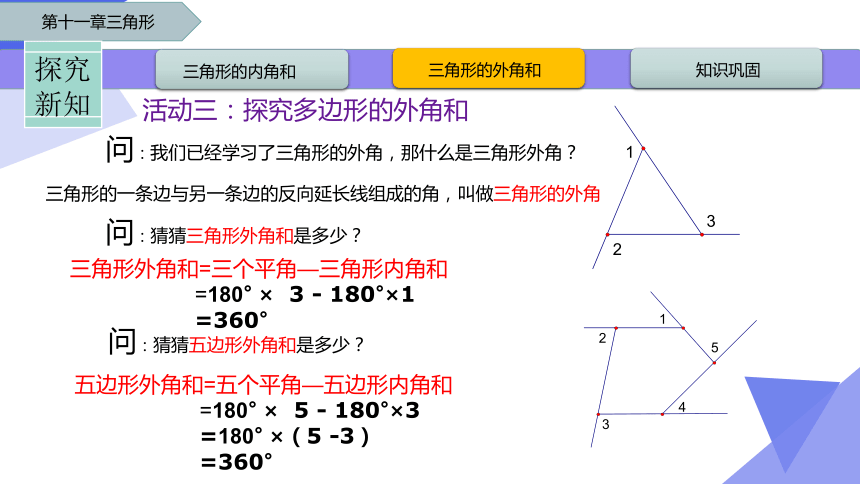
问:我们已经学习了三角形的外角,那什么是三角形外角?
活动三:探究多边形的外角和
三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角
问:猜猜三角形外角和是多少?
三角形外角和=三个平角—三角形内角和
=180° × 3 - 180°×1
=360°
问:猜猜五边形外角和是多少?
五边形外角和=五个平角—五边形内角和
=180° × 5 - 180°×3
=180° ×(5 -3)
=360°
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
活动三:探究多边形的外角和
四边形的外角和
=四个平角—四边形内角和
=4 ×180°-2×180°
=180°×(4-2)
=360°
六边形的外角和
=六个平角—六边形内角和
=6 ×180°-4×180°
=180°×(6-4)
=360°
八边形的外角和
=八个平角—八边形内角和
=8 ×180°-6×180°
=180°×(8-6)
=360°
结论:n边形的外角和等于360°.
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:(1)若一个正多边形的内角是120 °,那么这是_______边形.
(2)已知多边形的每个外角都是45°,则这个多边形是______边形.
正六
正八
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加. ( )
(2)当多边形边数增加时,它的外角和也随着增加. ( )
(3)三角形的外角和与八边形的外角和相等. ( )
(4)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-2)个三角形. ( )
2.五边形的内角和为 ,它的对角线有 条.
3.如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
练一练:
540°
5
180°
0°
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
120°
150°
2x°
x°
140°
x°
求下列图形中的X的值:
解:根据多边形内角和公式得:
120。+150。+90。+ x。+2x。= (5-2)×180°
360。+3x。=540。
3x。=180。
x。=60。
解:根据多边形内角和公式得:
140。+90。+x。+x。= (4-2)×180°
230。+2x。=360。
2x。= 130。
x。=65。
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
一个五边形,截去一个角后,形成了另一个多边形.
求截得的多边形的内角和
想一想:
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
11.3.2多边形的内角和
内角和计算公式
外角和
正多
边形
(n-2) × 180 °(n ≥3的整数)
多边形的外角和等于360°
特别注意:与边数无关。
内角= ,外角=
课堂小结
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
课后作业:
1、一个多边形除一个内角外其余各内角和1999°,求这个多边形的边数。
2、已知一个多边形,它的内角和等于外角和的2倍,
求这个多边形的边数。
谢谢!再见!
11.3.2多边形的内角和
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
导入新课
思考:是否任意四边形的内角和也等于3600?
A
B
C
D
三角形内角和180°
长方形/正方形:4×90°=360°
与三角形内角和有关吗?
有什么联系?
像黑板这种图形的内角和呢?
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
A
B
C
D
A
B
C
D
活动一:探究四边形的内角和
四边形:1800 × 2 = 3600
分割为两个三角形
提示:多边形内角和问题可以转化为三角形问题来解决.
思考:还有其他证法吗?
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
活动一:探究四边形的内角和
四个三角形的内角和—多出的周角
180°× 4 - 360° = 360°
三个三角形的内角和—多出的平角
180° × 3 - 180° = 360°
方法一:
方法二:
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
活动二:探究多边形的内角和
五边形
六边形
七边形
五边形的内角和
=3个三角形内角和
=3 ×1800 = 5400
六边形的内角和
=4个三角形内角和
=4×1800 = 7200
七边形的内角和
=5个三角形内角和
=5×1800 = 9000
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
活动二:探究多边形的内角和
多边形的边数 4 5 6 … n
图 形 …
从多边形一个顶点引出的对角线的条数 …
上面的对角线将多边形分成的三角形个数 …
多边形的内角和 …
4×180 °
3×180 °
2×180°
结论:n 边形的内角和为:(n-2)·180°
n -3
n -2
( n -2 )·180
1
2
3
2
3
4
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
问:我们已经学习了三角形的外角,那什么是三角形外角?
活动三:探究多边形的外角和
三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角
问:猜猜三角形外角和是多少?
三角形外角和=三个平角—三角形内角和
=180° × 3 - 180°×1
=360°
问:猜猜五边形外角和是多少?
五边形外角和=五个平角—五边形内角和
=180° × 5 - 180°×3
=180° ×(5 -3)
=360°
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
活动三:探究多边形的外角和
四边形的外角和
=四个平角—四边形内角和
=4 ×180°-2×180°
=180°×(4-2)
=360°
六边形的外角和
=六个平角—六边形内角和
=6 ×180°-4×180°
=180°×(6-4)
=360°
八边形的外角和
=八个平角—八边形内角和
=8 ×180°-6×180°
=180°×(8-6)
=360°
结论:n边形的外角和等于360°.
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
探究新知
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:(1)若一个正多边形的内角是120 °,那么这是_______边形.
(2)已知多边形的每个外角都是45°,则这个多边形是______边形.
正六
正八
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加. ( )
(2)当多边形边数增加时,它的外角和也随着增加. ( )
(3)三角形的外角和与八边形的外角和相等. ( )
(4)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-2)个三角形. ( )
2.五边形的内角和为 ,它的对角线有 条.
3.如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
练一练:
540°
5
180°
0°
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
120°
150°
2x°
x°
140°
x°
求下列图形中的X的值:
解:根据多边形内角和公式得:
120。+150。+90。+ x。+2x。= (5-2)×180°
360。+3x。=540。
3x。=180。
x。=60。
解:根据多边形内角和公式得:
140。+90。+x。+x。= (4-2)×180°
230。+2x。=360。
2x。= 130。
x。=65。
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
一个五边形,截去一个角后,形成了另一个多边形.
求截得的多边形的内角和
想一想:
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
11.3.2多边形的内角和
内角和计算公式
外角和
正多
边形
(n-2) × 180 °(n ≥3的整数)
多边形的外角和等于360°
特别注意:与边数无关。
内角= ,外角=
课堂小结
三角形的内角和
三角形的外角和
知识巩固
第十一章三角形
知识巩固
课后作业:
1、一个多边形除一个内角外其余各内角和1999°,求这个多边形的边数。
2、已知一个多边形,它的内角和等于外角和的2倍,
求这个多边形的边数。
谢谢!再见!
