人教版八年级上册 11.3.2多边形内角和 教案
文档属性
| 名称 | 人教版八年级上册 11.3.2多边形内角和 教案 | 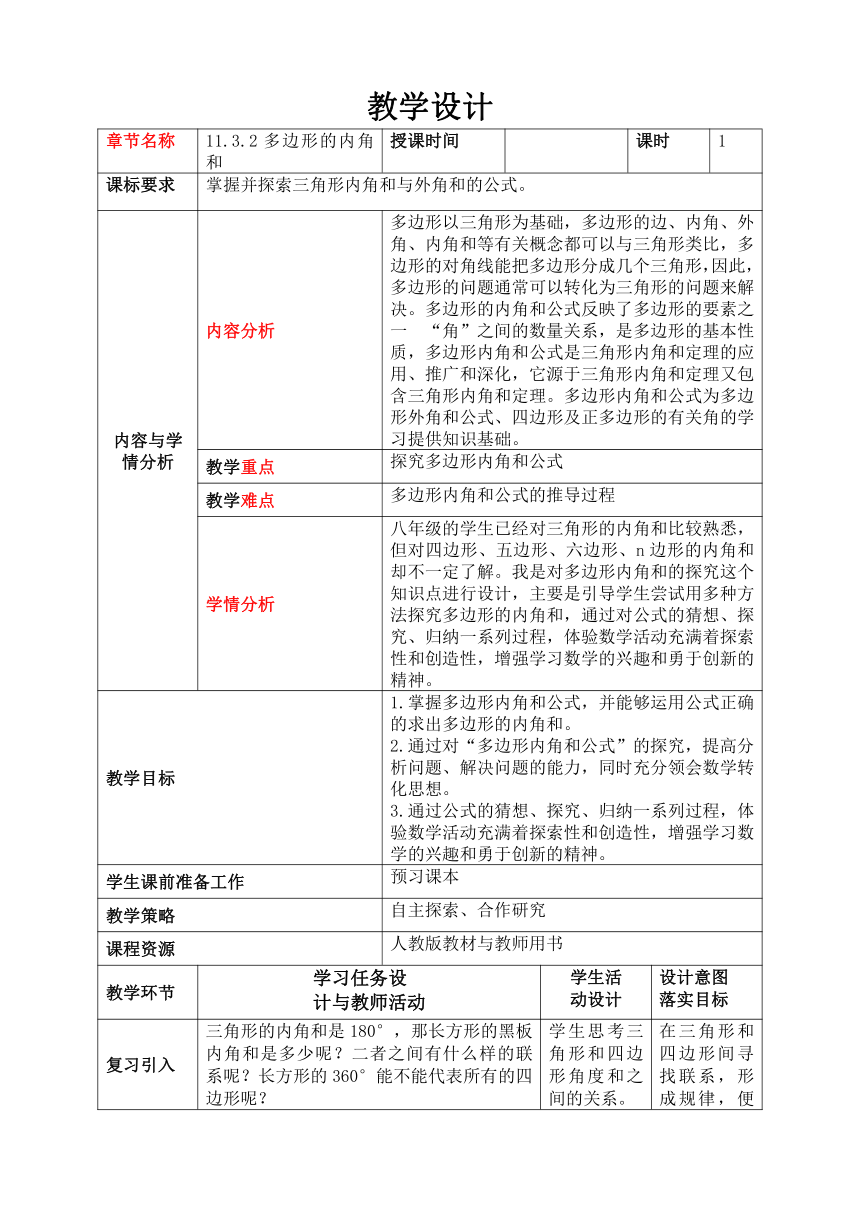 | |
| 格式 | docx | ||
| 文件大小 | 55.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 15:48:46 | ||
图片预览

文档简介
教学设计
章节名称 11.3.2多边形的内角和 授课时间 课时 1
课标要求 掌握并探索三角形内角和与外角和的公式。
内容与学 情分析 内容分析 多边形以三角形为基础,多边形的边、内角、外角、内角和等有关概念都可以与三角形类比,多边形的对角线能把多边形分成几个三角形,因此,多边形的问题通常可以转化为三角形的问题来解决。多边形的内角和公式反映了多边形的要素之一 “角”之间的数量关系,是多边形的基本性质,多边形内角和公式是三角形内角和定理的应用、推广和深化,它源于三角形内角和定理又包含三角形内角和定理。多边形内角和公式为多边形外角和公式、四边形及正多边形的有关角的学习提供知识基础。
教学重点 探究多边形内角和公式
教学难点 多边形内角和公式的推导过程
学情分析 八年级的学生已经对三角形的内角和比较熟悉,但对四边形、五边形、六边形、n边形的内角和却不一定了解。我是对多边形内角和的探究这个知识点进行设计,主要是引导学生尝试用多种方法探究多边形的内角和,通过对公式的猜想、探究、归纳一系列过程,体验数学活动充满着探索性和创造性,增强学习数学的兴趣和勇于创新的精神。
教学目标 1.掌握多边形内角和公式,并能够运用公式正确的求出多边形的内角和。 2.通过对“多边形内角和公式”的探究,提高分析问题、解决问题的能力,同时充分领会数学转化思想。 3.通过公式的猜想、探究、归纳一系列过程,体验数学活动充满着探索性和创造性,增强学习数学的兴趣和勇于创新的精神。
学生课前准备工作 预习课本
教学策略 自主探索、合作研究
课程资源 人教版教材与教师用书
教学环节 学习任务设计与教师活动 学生活 动设计 设计意图 落实目标
复习引入 三角形的内角和是180°,那长方形的黑板内角和是多少呢?二者之间有什么样的联系呢?长方形的360°能不能代表所有的四边形呢? 学生思考三角形和四边形角度和之间的关系。 在三角形和四边形间寻找联系,形成规律,便于记忆。
导入新课,合作学习 多边形内角和问题可以转化为三角形问题来解决. 方法一: 四个三角形的内角和—多出的周角 180°× 4 - 360° = 360° 三个三角形的内角和—多出的平角 180° × 3 - 180° = 360° 五边形的内角和 =3个三角形内角和 =3 ×1800 = 540° 六边形的内角和 =4个三角形内角和 =4×1800 = 720° 七边形的内角和=5个三角形内角和 =5×1800 = 900° 结论:n 边形的内角和为:(n-2)·180° 三角形外角和=三个平角—三角形内角和 =180° × 3 - 180°×1 =360° 五边形外角和=五个平角—五边形内角和 =180° × 5 - 180°×3 =180° ×(5 -3)=360° 回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么? 每个内角和的度数: 每个外角和的度数: 思考多边形与三角形间的联系,利用三角形计算多边形的内角和,并从多方面加以验证。 观察四边形的内角和,认识到四边形内角和是360°,五边形、六边形、N边形的内角和有着一定的规律性。 在教师引导下得出多边形内角和公式、外角和公式。 体验将图形分割求解的过程,从多种方式入手求解四边形的内角和,验证结果的在正确性。 让学生理解四边形、五边形甚至N边形的内角和之间存在着区别与联系,由特殊到一般进行总结。 最后进行规律总结,形成知识网络。
当堂训练 .判断. (1)当多边形边数增加时,它的内角和也随着增加. ( ) (2)当多边形边数增加时,它的外角和也随着增加. ( ) (3)三角形的外角和与八边形的外角和相等. ( ) (4)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-2)个三角形. 2.五边形的内角和为 ,它的对角线有 条. 3.如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______. 考察学生的知识掌握情况,方便找到着重点布置作业,巩固已经学会的知识,并了解学生的薄弱处。
小结 1、多边形内角和公式 : n边形内角和=(n-2)×180
作业 任务一:复习巩固11.3:5、6、7 任务二:剪一个四边形,证明内角和为360°
板书设计 多边形的内角和 每个内角和的度数: 每个外角和的度数:
反思
答案
九边形
三角形、六边形
AB//CD、BC//AD
章节名称 11.3.2多边形的内角和 授课时间 课时 1
课标要求 掌握并探索三角形内角和与外角和的公式。
内容与学 情分析 内容分析 多边形以三角形为基础,多边形的边、内角、外角、内角和等有关概念都可以与三角形类比,多边形的对角线能把多边形分成几个三角形,因此,多边形的问题通常可以转化为三角形的问题来解决。多边形的内角和公式反映了多边形的要素之一 “角”之间的数量关系,是多边形的基本性质,多边形内角和公式是三角形内角和定理的应用、推广和深化,它源于三角形内角和定理又包含三角形内角和定理。多边形内角和公式为多边形外角和公式、四边形及正多边形的有关角的学习提供知识基础。
教学重点 探究多边形内角和公式
教学难点 多边形内角和公式的推导过程
学情分析 八年级的学生已经对三角形的内角和比较熟悉,但对四边形、五边形、六边形、n边形的内角和却不一定了解。我是对多边形内角和的探究这个知识点进行设计,主要是引导学生尝试用多种方法探究多边形的内角和,通过对公式的猜想、探究、归纳一系列过程,体验数学活动充满着探索性和创造性,增强学习数学的兴趣和勇于创新的精神。
教学目标 1.掌握多边形内角和公式,并能够运用公式正确的求出多边形的内角和。 2.通过对“多边形内角和公式”的探究,提高分析问题、解决问题的能力,同时充分领会数学转化思想。 3.通过公式的猜想、探究、归纳一系列过程,体验数学活动充满着探索性和创造性,增强学习数学的兴趣和勇于创新的精神。
学生课前准备工作 预习课本
教学策略 自主探索、合作研究
课程资源 人教版教材与教师用书
教学环节 学习任务设计与教师活动 学生活 动设计 设计意图 落实目标
复习引入 三角形的内角和是180°,那长方形的黑板内角和是多少呢?二者之间有什么样的联系呢?长方形的360°能不能代表所有的四边形呢? 学生思考三角形和四边形角度和之间的关系。 在三角形和四边形间寻找联系,形成规律,便于记忆。
导入新课,合作学习 多边形内角和问题可以转化为三角形问题来解决. 方法一: 四个三角形的内角和—多出的周角 180°× 4 - 360° = 360° 三个三角形的内角和—多出的平角 180° × 3 - 180° = 360° 五边形的内角和 =3个三角形内角和 =3 ×1800 = 540° 六边形的内角和 =4个三角形内角和 =4×1800 = 720° 七边形的内角和=5个三角形内角和 =5×1800 = 900° 结论:n 边形的内角和为:(n-2)·180° 三角形外角和=三个平角—三角形内角和 =180° × 3 - 180°×1 =360° 五边形外角和=五个平角—五边形内角和 =180° × 5 - 180°×3 =180° ×(5 -3)=360° 回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么? 每个内角和的度数: 每个外角和的度数: 思考多边形与三角形间的联系,利用三角形计算多边形的内角和,并从多方面加以验证。 观察四边形的内角和,认识到四边形内角和是360°,五边形、六边形、N边形的内角和有着一定的规律性。 在教师引导下得出多边形内角和公式、外角和公式。 体验将图形分割求解的过程,从多种方式入手求解四边形的内角和,验证结果的在正确性。 让学生理解四边形、五边形甚至N边形的内角和之间存在着区别与联系,由特殊到一般进行总结。 最后进行规律总结,形成知识网络。
当堂训练 .判断. (1)当多边形边数增加时,它的内角和也随着增加. ( ) (2)当多边形边数增加时,它的外角和也随着增加. ( ) (3)三角形的外角和与八边形的外角和相等. ( ) (4)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-2)个三角形. 2.五边形的内角和为 ,它的对角线有 条. 3.如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______. 考察学生的知识掌握情况,方便找到着重点布置作业,巩固已经学会的知识,并了解学生的薄弱处。
小结 1、多边形内角和公式 : n边形内角和=(n-2)×180
作业 任务一:复习巩固11.3:5、6、7 任务二:剪一个四边形,证明内角和为360°
板书设计 多边形的内角和 每个内角和的度数: 每个外角和的度数:
反思
答案
九边形
三角形、六边形
AB//CD、BC//AD
