27.1 图形的相似 课件(共23张PPT)
文档属性
| 名称 | 27.1 图形的相似 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 18:08:50 | ||
图片预览








文档简介
(共23张PPT)
人教版数学九年级下册
第27章 相似
27.1 图形的相似
第1课时 相似图形
一、教学目标
二、教学重难点
重点
难点
1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形的概念.
2.经历观察和操作的过程,探索图形的相似,掌握相似图形的性质,会用其性质解决有关问题.
3.在探究相似图形的过程中,培养与他人交流、合作的意识和品质.
初步认识相似图形.
识别相似图形.
活动1 新课导入
三、教学设计
观察所给出的几组图形(多媒体展示教材P24四组图片),说说它们有哪些共同点.
活动2 探究新知
1.教材P24.
提出问题:
(1)图27.1-1给我们以什么样的形象?
(2)两个相似图形,可以经过怎样的变换得到?
(3)在日常生活中你还见过哪些相似的图形?
分析答案,提出疑惑,共同解决.
2.教材P25思考.
提出问题:
(1)平面镜得到的人的形象与本人相似吗?
(2)哈哈镜中的人体形象与本人相似吗?为什么?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.我们把__________________叫做相似图形.
2.将图形放大、缩小后得到的图形与原图形是____________.
形状相同的图形
相似图形
活动4 例题与练习
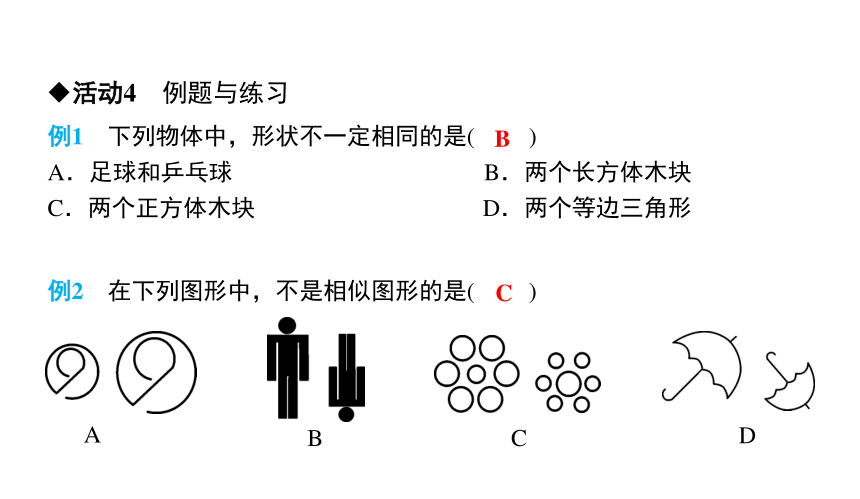
例1 下列物体中,形状不一定相同的是( )
A.足球和乒乓球 B.两个长方体木块
C.两个正方体木块 D.两个等边三角形
B
例2 在下列图形中,不是相似图形的是( )
A
B
C
D
C
例3 在平面直角坐标系中描出点A(-1,0),B(1,0),C(2,2),用线段顺次连接起来,得到△ABC.
(1)把A,B,C各点横、纵坐标都减去1,得到△A1B1C1,画出△A1B1C1,则△A1B1C1与△ABC相似吗?
(2)把A,B,C各点横、纵坐标都乘以2,得到△A2B2C2,画出△A2B2C2,则△A2B2C2与△ABC相似吗?
解:(1)A1(-2,-1),B1(0,-1),C1(1,1).(画图略)△A1B1C1与△ABC相似,平移得到,形状没有变化;
(2)A2(-2,0),B2(2,0),C2(4,4).(画图略)△A2B2C2与△ABC相似,扩大2倍得到.
练 习
1.教材P25练习第1,2题.
2.下列说法正确的有( )
①同一底片印出来的不同尺寸的照片是相似的;②放电影时胶片上的图象和它映射到屏幕上的图象是相似的;③放大镜放大后的图形与原来的图形是相似的.
A.0个 B.1个 C.2个 D.3个
D
练 习
3.仔细观察图中五组图形,两个图形相似的有________.(填序号)
4.如图,图形中相似的正方形共有____个,相似的三角形共有____个.
①⑤
5
16
人教版数学九年级下册
第27章 相似
27.1 图形的相似
第2课时 相似多边形
一、教学目标
1.理解相似多边形和相似比的概念,掌握相似多边形的两个基本性质.
2.理解四条线段是“成比例线段”的概念,掌握比例的基本性质,并能进行相关的计算.
3.掌握相似多边形的主要特征,能够识别两个多边形是否相似,并能运用其性质进行相关的计算.
二、教学重难点
重点
难点
掌握相似多边形的性质及判别方法,能用性质解决具体问题.
判别两个多边形是否相似.
活动1 新课导入
三、教学设计
1.什么是相似图形?
形状相同的图形
2.举几个相似图形的例子.
大小不同的两副三角板,大小不同的两张中国地图等
活动2 探究新知
思考完成并交流展示.
1.教材P26.
提出问题:
(1)判定两个多边形相似必须具备的条件是什么?
(2)图形A和图形B的相似比与图形B和图形A的相似比一样吗?
(3)如何寻找对应角、对应边?可从中建立什么数量关系?
(4)如何应用相似多边形的性质求未知的边或角的大小?
2.教材P26右上角(成比例线段的概念).
提出问题:
(1)理解成比例线段时应注意什么?
(2)对于比例式 中,a与d,b与c的位置可以互换吗?为什么?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.两个________相同的多边形,如果它们的_____分别相等,______成比例,那么这两个多边形叫做相似多边形.
2.对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc),我们就说这四条线段成比例.
边数
角
边
活动4 例题与练习
如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
21cm
24cm
G
E
F
H
α
x
118°
D
A
B
C
18cm
78°
83°
β
例1 教材P26例题.
在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得
解得 x=28cm.
21cm
24cm
G
E
F
H
α
x
118°
D
A
B
C
18cm
78°
83°
β
例2 如图,矩形ABCD与矩形EFGH相似吗?若相似,请加以证明;若不相似,请说明理由.
解:矩形ABCD与矩形EFGH相似.
证明如下:∵四边形ABCD与四边形EFGH都为矩形,
∴∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=90°.
∵AD=BC=4 cm,DC=AB=2 cm,
EH=FG=2.4 cm,EF=HG=1.2 cm,
∴矩形ABCD与矩形EFGH相似.
练 习
1.教材P27练习第1,2,3题.
2.某机器零件在图纸上的长度是21 mm,它的实际长度是630 mm,则图纸的比例尺为( )
A.1∶20 B.1∶30 C.1∶40 D.1∶50
3.下列各线段的长度成比例的是( )
A.2 cm,5 cm,6 cm,8 cm B.1 cm,2 cm,3 cm,4 cm
C.3 cm,6 cm,7 cm,9 cm D.3 cm,6 cm,9 cm,18 cm
B
D
练 习
4.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
解:(1)由已知,得MN=AB,MD= AD= BC.
∵矩形DMNC与矩形ABCD相似,
∵AB=4,
谢谢观看
人教版数学九年级下册
第27章 相似
27.1 图形的相似
第1课时 相似图形
一、教学目标
二、教学重难点
重点
难点
1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形的概念.
2.经历观察和操作的过程,探索图形的相似,掌握相似图形的性质,会用其性质解决有关问题.
3.在探究相似图形的过程中,培养与他人交流、合作的意识和品质.
初步认识相似图形.
识别相似图形.
活动1 新课导入
三、教学设计
观察所给出的几组图形(多媒体展示教材P24四组图片),说说它们有哪些共同点.
活动2 探究新知
1.教材P24.
提出问题:
(1)图27.1-1给我们以什么样的形象?
(2)两个相似图形,可以经过怎样的变换得到?
(3)在日常生活中你还见过哪些相似的图形?
分析答案,提出疑惑,共同解决.
2.教材P25思考.
提出问题:
(1)平面镜得到的人的形象与本人相似吗?
(2)哈哈镜中的人体形象与本人相似吗?为什么?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.我们把__________________叫做相似图形.
2.将图形放大、缩小后得到的图形与原图形是____________.
形状相同的图形
相似图形
活动4 例题与练习
例1 下列物体中,形状不一定相同的是( )
A.足球和乒乓球 B.两个长方体木块
C.两个正方体木块 D.两个等边三角形
B
例2 在下列图形中,不是相似图形的是( )
A
B
C
D
C
例3 在平面直角坐标系中描出点A(-1,0),B(1,0),C(2,2),用线段顺次连接起来,得到△ABC.
(1)把A,B,C各点横、纵坐标都减去1,得到△A1B1C1,画出△A1B1C1,则△A1B1C1与△ABC相似吗?
(2)把A,B,C各点横、纵坐标都乘以2,得到△A2B2C2,画出△A2B2C2,则△A2B2C2与△ABC相似吗?
解:(1)A1(-2,-1),B1(0,-1),C1(1,1).(画图略)△A1B1C1与△ABC相似,平移得到,形状没有变化;
(2)A2(-2,0),B2(2,0),C2(4,4).(画图略)△A2B2C2与△ABC相似,扩大2倍得到.
练 习
1.教材P25练习第1,2题.
2.下列说法正确的有( )
①同一底片印出来的不同尺寸的照片是相似的;②放电影时胶片上的图象和它映射到屏幕上的图象是相似的;③放大镜放大后的图形与原来的图形是相似的.
A.0个 B.1个 C.2个 D.3个
D
练 习
3.仔细观察图中五组图形,两个图形相似的有________.(填序号)
4.如图,图形中相似的正方形共有____个,相似的三角形共有____个.
①⑤
5
16
人教版数学九年级下册
第27章 相似
27.1 图形的相似
第2课时 相似多边形
一、教学目标
1.理解相似多边形和相似比的概念,掌握相似多边形的两个基本性质.
2.理解四条线段是“成比例线段”的概念,掌握比例的基本性质,并能进行相关的计算.
3.掌握相似多边形的主要特征,能够识别两个多边形是否相似,并能运用其性质进行相关的计算.
二、教学重难点
重点
难点
掌握相似多边形的性质及判别方法,能用性质解决具体问题.
判别两个多边形是否相似.
活动1 新课导入
三、教学设计
1.什么是相似图形?
形状相同的图形
2.举几个相似图形的例子.
大小不同的两副三角板,大小不同的两张中国地图等
活动2 探究新知
思考完成并交流展示.
1.教材P26.
提出问题:
(1)判定两个多边形相似必须具备的条件是什么?
(2)图形A和图形B的相似比与图形B和图形A的相似比一样吗?
(3)如何寻找对应角、对应边?可从中建立什么数量关系?
(4)如何应用相似多边形的性质求未知的边或角的大小?
2.教材P26右上角(成比例线段的概念).
提出问题:
(1)理解成比例线段时应注意什么?
(2)对于比例式 中,a与d,b与c的位置可以互换吗?为什么?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.两个________相同的多边形,如果它们的_____分别相等,______成比例,那么这两个多边形叫做相似多边形.
2.对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc),我们就说这四条线段成比例.
边数
角
边
活动4 例题与练习
如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
21cm
24cm
G
E
F
H
α
x
118°
D
A
B
C
18cm
78°
83°
β
例1 教材P26例题.
在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得
解得 x=28cm.
21cm
24cm
G
E
F
H
α
x
118°
D
A
B
C
18cm
78°
83°
β
例2 如图,矩形ABCD与矩形EFGH相似吗?若相似,请加以证明;若不相似,请说明理由.
解:矩形ABCD与矩形EFGH相似.
证明如下:∵四边形ABCD与四边形EFGH都为矩形,
∴∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=90°.
∵AD=BC=4 cm,DC=AB=2 cm,
EH=FG=2.4 cm,EF=HG=1.2 cm,
∴矩形ABCD与矩形EFGH相似.
练 习
1.教材P27练习第1,2,3题.
2.某机器零件在图纸上的长度是21 mm,它的实际长度是630 mm,则图纸的比例尺为( )
A.1∶20 B.1∶30 C.1∶40 D.1∶50
3.下列各线段的长度成比例的是( )
A.2 cm,5 cm,6 cm,8 cm B.1 cm,2 cm,3 cm,4 cm
C.3 cm,6 cm,7 cm,9 cm D.3 cm,6 cm,9 cm,18 cm
B
D
练 习
4.如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
解:(1)由已知,得MN=AB,MD= AD= BC.
∵矩形DMNC与矩形ABCD相似,
∵AB=4,
谢谢观看
