27.2.1 相似三角形的判定 课件(共37张PPT)
文档属性
| 名称 | 27.2.1 相似三角形的判定 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-24 18:11:02 | ||
图片预览








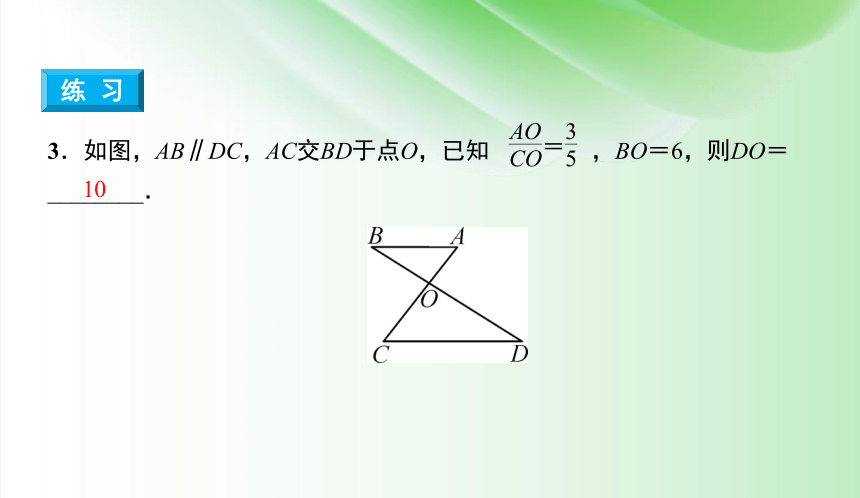
文档简介
(共37张PPT)
人教版数学九年级下册
第27章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例定理
一、教学目标
二、教学重难点
重点
难点
1.理解相似三角形的概念,了解相似三角形的对应元素及相似比.
2.掌握平行线分线段成比例及其两个推论.
3.掌握判定两个三角形相似的预备定理及其应用.
平行线分线段成比例定理及相似三角形的预备定理及应用.
两个定理的探索过程.
活动1 新课导入
三、教学设计
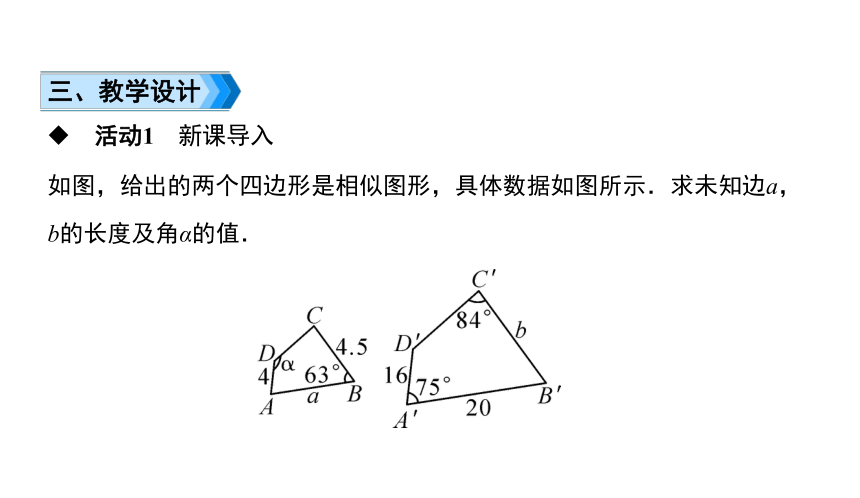
如图,给出的两个四边形是相似图形,具体数据如图所示.求未知边a,b的长度及角α的值.
活动2 探究新知
思考完成并交流展示.
1.教材P29“探究”以上内容.
提出问题:
(1)如果k=1,这两个三角形有怎样的关系?
(2)当△A′B′C′∽△ABC时,相似比是多少?如何表示?
(3)若△ABC∽△A′B′C′,△A′B′C′∽△A″B″C″,则△ABC∽△A″B″C″吗?
2.教材P29~30“思考”以上内容.
(1)图27.2-2中,当 的值为1时,这组平行线有什么特点?
(2)图27.2-3中,除了分线段成比例外,还有其他的比例关系吗?
分析答案,提出疑惑,共同解决.
3.教材P30思考.
提出问题:
(1)体会过点E作与AB平行的直线EF的作用,为什么要作这条辅助线?
(2)过点D作与AC平行的直线与BC相交,可否证明△ADE∽△ABC?如果在三角形中出现一边的平行线,那么你应该联想到什么?
(3)如图,若点D,E分别在AB,AC的反向延长线上,△ADE与△ABC是否还相似?
活动3 知识归纳
1.两个三角形三个角分别相等,三条边成比例,那么这两个三角形相似.
强调:(1)用“∽”表示两三角形相似时,一般应将对应点写在对应的位置上;
(2)若△ABC与△A′B′C′的相似比是k,则△A′B′C′与△ABC的相似比是____.
2.平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例.
3.平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段____________.
4.相似三角形判定的预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形__________.
成比例
相似
活动4 例题与练习
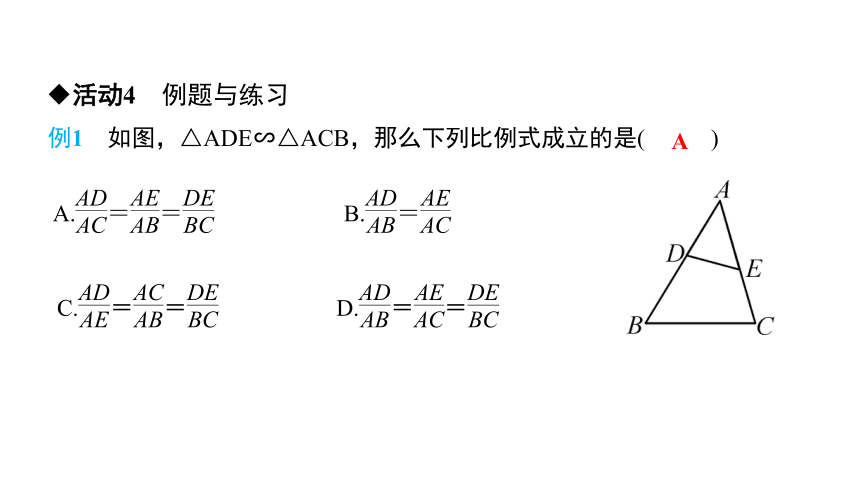
例1 如图,△ADE∽△ACB,那么下列比例式成立的是( )
A
例2 如图,在 ABCD中,AE=EB,AF=2,求CF的长.
解:∵四边形ABCD为平行四边形,
∵AE=EB,
∴CF=2AF=4.
∴AB∥CD,AB=CD.
∴△AEF∽△CDF,
练 习
1.教材P31练习第1,2题.
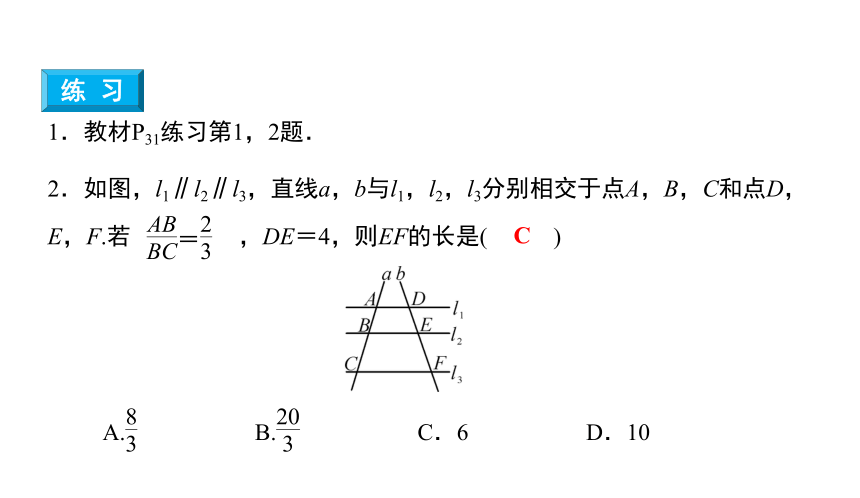
2.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若 ,DE=4,则EF的长是( )
C
练 习
3.如图,AB∥DC,AC交BD于点O,已知 ,BO=6,则DO=________.
10
4.如图,已知菱形BEDF内接于△ABC,点E,D,F分别在边AB,AC和BC上.若AB=15 cm,BC=12 cm,求菱形BEDF的边长.
解:设菱形BEDF的边长为x cm,则AE=(15-x)cm.
∵四边形BEDF是菱形,
∴DE∥BC,∴△AED∽△ABC,
∵AB=15 cm,BC=12 cm,AE=(15-x)cm,
∴菱形BEDF的边长为 cm.
人教版数学九年级下册
第27章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第2课时 三边成比例或两边成比例且夹角相等的两个三角形相似
一、教学目标
二、教学重难点
重点
难点
1.掌握相似三角形的判定定理1,2.
2.会用判定定理判定两个三角形相似.
相似三角形的判定定理1,2的运用.
相似三角形判定定理的证明.
活动1 新课导入
三、教学设计
1.如图,AB∥CD,AE=3,DE=2,则 =______.
2.如图,已知AB∥CD∥EF,则下列结论不正确的是( )
3.判定两个三角形全等我们有SSS,SAS,ASA,AAS等方法,类似地,判定两个三角形相似是否也有类似的简单方法呢?
C
活动2 探究新知
1.教材P32探究.
提出问题:
(1)改变任意角或k值的大小,再试一试,是否有同样的结论?
(2)体会证明过程中△A′DE的作用.
2.教材P33.
提出问题:
(1)尝试证明“两边成比例且夹角相等的两个三角形相似”;
(2)若把图27.2-8中的条件“∠A=∠A′”换成“∠B=∠B′”,那么两个三角形一定相似吗?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.三边__________的两个三角形相似.
2.两边成比例且夹角_______的两个三角形相似.
成比例
相等
活动4 例题与练习
例1 教材P33例1.
例2 在△ABC中,AB=6,AC=8,在△DEF中,DE=4,DF=3,要使△ABC与△DFE相似,需添加的一个条件是_______________________.(写出一种情况即可)
BC=2EF(或∠A=∠D)
例3 如图,在梯形ABCD中,∠A=∠B=90°,AB=7,AD=2,BC=3,如果边AB上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,求AP的长.
解:设AP=x,则BP=7-x.
(1)当△APD∽△BCP时,则 ,即 ,
解得x=1或x=6,符合条件;
(2)当△APD∽△BPC时,则 ,即 ,解得x= ,符合条件.综上所述,AP的长是1或6或.
练 习
1.教材P34练习第1,2,3题.
2.如图,在 ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是( )
A.5 B.8.2 C.6.4 D.1.8
D
练 习
3.如图,在正方形网格上画出梯形ABCD,连接BD,则∠BDC的度数是_______.
135°
4.如图,在△ABC中,∠C=90°,D,E分别是AB,AC上的点,且AD·AB=AE·AC,那么ED与AB垂直吗?请说明理由.
解:ED与AB垂直.
理由如下:由AD·AB=AE·AC,
又∵∠A=∠A,可证明△ADE∽△ACB,
∴∠ADE=∠C=90°,即DE⊥AB.
人教版数学九年级下册
第27章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时 两角分别相等的两个三角形相似
一、教学目标
二、教学重难点
重点
难点
1.掌握相似三角形的判定方法3和直角三角形相似,并运用它们解决一些实际问题.
2.经历探究相似三角形的判定,体会类比思想在学习数学中的作用.
掌握相似三角形的判定定理3及直角三角形中特有的相似判定方法.
探究两个判定定理的证明过程.
活动1 新课导入
三、教学设计
1.展示大三角板(45°和45°)及学生用的小三角尺(45°和45°),观察这样的两个三角形相似吗?
2.如果一个三角形中的两个角与另一个三角形中的两个角对应相等,这样的两个三角形相似吗?
活动2 探究新知
思考完成并交流展示.
1.教材P35例2以上内容.
提出问题:
(1)作△ABC和△A′B′C′,使∠A=∠A′,∠B=∠B′,分别度量这两个三角形的边长,计算 的值,你有什么发现?由此你能做出一个怎样的猜想?
(2)尝试证明“两角分别相等的两个三角形相似”.
2.教材P36思考.
提出问题:
(1)直角三角形三边存在什么关系?
(2)已知两边成比例,如何判定两直角三角形相似?
分析答案,提出疑惑,共同解决.
1.两角分别相等的两个三角形相似.
2.两直角三角形相似的判定方法:
①一锐角对应相等;
②两直角边对应成比例;
③斜边和一直角边对应成比例.
活动3 知识归纳
3.思考:总结一下,两等腰三角形相似的判定方法有哪些?两等边三角形,两等腰直角三角形相似的判定方法呢?
两等腰三角形相似的判定方法有:
①顶角相等;
②底角相等;
③腰和底对应成比例.
所有等边三角形都相似,所有等腰直角三角形都相似.
活动4 例题与练习
例1 教材P35例2.
例2 如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.若AB=6,AD=5,求AF的长.
解:如图.连接BD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD2=AB2-AD2=11.
∵∠2=∠3,∠2=∠1,
∴∠1=∠3.
∵∠ADB=∠BDF=90°,
∴△DFB∽△DBA,
∴BD2=AD·DF,
例3 如图,在△ABC与△ADB中,∠ABC=∠ADB=90°,AC=10 cm,AB=8 cm,如果图中的两个直角三角形相似,求AD的长.
解:∵∠ABC=∠ADB=90°,
∴当△ABC∽△ADB时,
∴AD=6.4 cm;当△ABC∽△BDA时,
∴BD=6.4 cm,
综上所述,AD的长为6.4 cm或4.8 cm.
练 习
1.教材P36练习第1,2,3题.
2.如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C
D
练 习
3.在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=12,AB=15,A′C′=8,则当A′B′=______时,△ABC∽△A′B′C′.
4.如图,BD是⊙O的直径,A,C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.求证:△ABD∽△AEB.
证明:∵AB=AC,
∴∠ADB=∠ABC.
又∵∠BAE=∠DAB,
∴△ABD∽△AEB.
∴AB=AC,
⌒
⌒
10
谢谢观看
人教版数学九年级下册
第27章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例定理
一、教学目标
二、教学重难点
重点
难点
1.理解相似三角形的概念,了解相似三角形的对应元素及相似比.
2.掌握平行线分线段成比例及其两个推论.
3.掌握判定两个三角形相似的预备定理及其应用.
平行线分线段成比例定理及相似三角形的预备定理及应用.
两个定理的探索过程.
活动1 新课导入
三、教学设计
如图,给出的两个四边形是相似图形,具体数据如图所示.求未知边a,b的长度及角α的值.
活动2 探究新知
思考完成并交流展示.
1.教材P29“探究”以上内容.
提出问题:
(1)如果k=1,这两个三角形有怎样的关系?
(2)当△A′B′C′∽△ABC时,相似比是多少?如何表示?
(3)若△ABC∽△A′B′C′,△A′B′C′∽△A″B″C″,则△ABC∽△A″B″C″吗?
2.教材P29~30“思考”以上内容.
(1)图27.2-2中,当 的值为1时,这组平行线有什么特点?
(2)图27.2-3中,除了分线段成比例外,还有其他的比例关系吗?
分析答案,提出疑惑,共同解决.
3.教材P30思考.
提出问题:
(1)体会过点E作与AB平行的直线EF的作用,为什么要作这条辅助线?
(2)过点D作与AC平行的直线与BC相交,可否证明△ADE∽△ABC?如果在三角形中出现一边的平行线,那么你应该联想到什么?
(3)如图,若点D,E分别在AB,AC的反向延长线上,△ADE与△ABC是否还相似?
活动3 知识归纳
1.两个三角形三个角分别相等,三条边成比例,那么这两个三角形相似.
强调:(1)用“∽”表示两三角形相似时,一般应将对应点写在对应的位置上;
(2)若△ABC与△A′B′C′的相似比是k,则△A′B′C′与△ABC的相似比是____.
2.平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例.
3.平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段____________.
4.相似三角形判定的预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形__________.
成比例
相似
活动4 例题与练习
例1 如图,△ADE∽△ACB,那么下列比例式成立的是( )
A
例2 如图,在 ABCD中,AE=EB,AF=2,求CF的长.
解:∵四边形ABCD为平行四边形,
∵AE=EB,
∴CF=2AF=4.
∴AB∥CD,AB=CD.
∴△AEF∽△CDF,
练 习
1.教材P31练习第1,2题.
2.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若 ,DE=4,则EF的长是( )
C
练 习
3.如图,AB∥DC,AC交BD于点O,已知 ,BO=6,则DO=________.
10
4.如图,已知菱形BEDF内接于△ABC,点E,D,F分别在边AB,AC和BC上.若AB=15 cm,BC=12 cm,求菱形BEDF的边长.
解:设菱形BEDF的边长为x cm,则AE=(15-x)cm.
∵四边形BEDF是菱形,
∴DE∥BC,∴△AED∽△ABC,
∵AB=15 cm,BC=12 cm,AE=(15-x)cm,
∴菱形BEDF的边长为 cm.
人教版数学九年级下册
第27章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第2课时 三边成比例或两边成比例且夹角相等的两个三角形相似
一、教学目标
二、教学重难点
重点
难点
1.掌握相似三角形的判定定理1,2.
2.会用判定定理判定两个三角形相似.
相似三角形的判定定理1,2的运用.
相似三角形判定定理的证明.
活动1 新课导入
三、教学设计
1.如图,AB∥CD,AE=3,DE=2,则 =______.
2.如图,已知AB∥CD∥EF,则下列结论不正确的是( )
3.判定两个三角形全等我们有SSS,SAS,ASA,AAS等方法,类似地,判定两个三角形相似是否也有类似的简单方法呢?
C
活动2 探究新知
1.教材P32探究.
提出问题:
(1)改变任意角或k值的大小,再试一试,是否有同样的结论?
(2)体会证明过程中△A′DE的作用.
2.教材P33.
提出问题:
(1)尝试证明“两边成比例且夹角相等的两个三角形相似”;
(2)若把图27.2-8中的条件“∠A=∠A′”换成“∠B=∠B′”,那么两个三角形一定相似吗?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.三边__________的两个三角形相似.
2.两边成比例且夹角_______的两个三角形相似.
成比例
相等
活动4 例题与练习
例1 教材P33例1.
例2 在△ABC中,AB=6,AC=8,在△DEF中,DE=4,DF=3,要使△ABC与△DFE相似,需添加的一个条件是_______________________.(写出一种情况即可)
BC=2EF(或∠A=∠D)
例3 如图,在梯形ABCD中,∠A=∠B=90°,AB=7,AD=2,BC=3,如果边AB上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,求AP的长.
解:设AP=x,则BP=7-x.
(1)当△APD∽△BCP时,则 ,即 ,
解得x=1或x=6,符合条件;
(2)当△APD∽△BPC时,则 ,即 ,解得x= ,符合条件.综上所述,AP的长是1或6或.
练 习
1.教材P34练习第1,2,3题.
2.如图,在 ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是( )
A.5 B.8.2 C.6.4 D.1.8
D
练 习
3.如图,在正方形网格上画出梯形ABCD,连接BD,则∠BDC的度数是_______.
135°
4.如图,在△ABC中,∠C=90°,D,E分别是AB,AC上的点,且AD·AB=AE·AC,那么ED与AB垂直吗?请说明理由.
解:ED与AB垂直.
理由如下:由AD·AB=AE·AC,
又∵∠A=∠A,可证明△ADE∽△ACB,
∴∠ADE=∠C=90°,即DE⊥AB.
人教版数学九年级下册
第27章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时 两角分别相等的两个三角形相似
一、教学目标
二、教学重难点
重点
难点
1.掌握相似三角形的判定方法3和直角三角形相似,并运用它们解决一些实际问题.
2.经历探究相似三角形的判定,体会类比思想在学习数学中的作用.
掌握相似三角形的判定定理3及直角三角形中特有的相似判定方法.
探究两个判定定理的证明过程.
活动1 新课导入
三、教学设计
1.展示大三角板(45°和45°)及学生用的小三角尺(45°和45°),观察这样的两个三角形相似吗?
2.如果一个三角形中的两个角与另一个三角形中的两个角对应相等,这样的两个三角形相似吗?
活动2 探究新知
思考完成并交流展示.
1.教材P35例2以上内容.
提出问题:
(1)作△ABC和△A′B′C′,使∠A=∠A′,∠B=∠B′,分别度量这两个三角形的边长,计算 的值,你有什么发现?由此你能做出一个怎样的猜想?
(2)尝试证明“两角分别相等的两个三角形相似”.
2.教材P36思考.
提出问题:
(1)直角三角形三边存在什么关系?
(2)已知两边成比例,如何判定两直角三角形相似?
分析答案,提出疑惑,共同解决.
1.两角分别相等的两个三角形相似.
2.两直角三角形相似的判定方法:
①一锐角对应相等;
②两直角边对应成比例;
③斜边和一直角边对应成比例.
活动3 知识归纳
3.思考:总结一下,两等腰三角形相似的判定方法有哪些?两等边三角形,两等腰直角三角形相似的判定方法呢?
两等腰三角形相似的判定方法有:
①顶角相等;
②底角相等;
③腰和底对应成比例.
所有等边三角形都相似,所有等腰直角三角形都相似.
活动4 例题与练习
例1 教材P35例2.
例2 如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.若AB=6,AD=5,求AF的长.
解:如图.连接BD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD2=AB2-AD2=11.
∵∠2=∠3,∠2=∠1,
∴∠1=∠3.
∵∠ADB=∠BDF=90°,
∴△DFB∽△DBA,
∴BD2=AD·DF,
例3 如图,在△ABC与△ADB中,∠ABC=∠ADB=90°,AC=10 cm,AB=8 cm,如果图中的两个直角三角形相似,求AD的长.
解:∵∠ABC=∠ADB=90°,
∴当△ABC∽△ADB时,
∴AD=6.4 cm;当△ABC∽△BDA时,
∴BD=6.4 cm,
综上所述,AD的长为6.4 cm或4.8 cm.
练 习
1.教材P36练习第1,2,3题.
2.如图,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C
D
练 习
3.在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=12,AB=15,A′C′=8,则当A′B′=______时,△ABC∽△A′B′C′.
4.如图,BD是⊙O的直径,A,C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.求证:△ABD∽△AEB.
证明:∵AB=AC,
∴∠ADB=∠ABC.
又∵∠BAE=∠DAB,
∴△ABD∽△AEB.
∴AB=AC,
⌒
⌒
10
谢谢观看
