29.1 投影 课件(共25张PPT)
图片预览






文档简介
(共25张PPT)
人教版数学九年级下册
第29章 投影与视图
29.1 投影
第1课时 平行投影与中心投影
一、教学目标
二、教学重难点
重点
难点
1.经历实践探索,了解投影、平行投影与中心投影的概念.
2.了解平行投影与中心投影的区别.
3.学会关注生活中有关投影的数学问题,提高数学应用意识.
理解投影的概念.
掌握中心投影与平行投影的联系与区别.
活动1 新课导入
三、教学设计
感受日常生活中的一些投影现象.
活动2 探究新知
1.教材P87部分内容.
提出问题:
(1)什么叫投影?什么叫投影线?什么叫投影面?
(2)什么叫平行投影?
(3)请例举生活中平行投影的例子.
2.教材P88练习以上部分.
提出问题:
(1)什么叫中心投影?请例举一些中心投影的例子;
(2)平行投影和中心投影的区别是什么?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.用_______照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,____________叫做投影线,________所在的平面叫做投影面.
2.由__________形成的投影叫做平行投影,由________ (点光源)发出的光线形成的投影叫做中心投影.
光线
照射光线
投影
平行光线
同一点
活动4 例题与练习
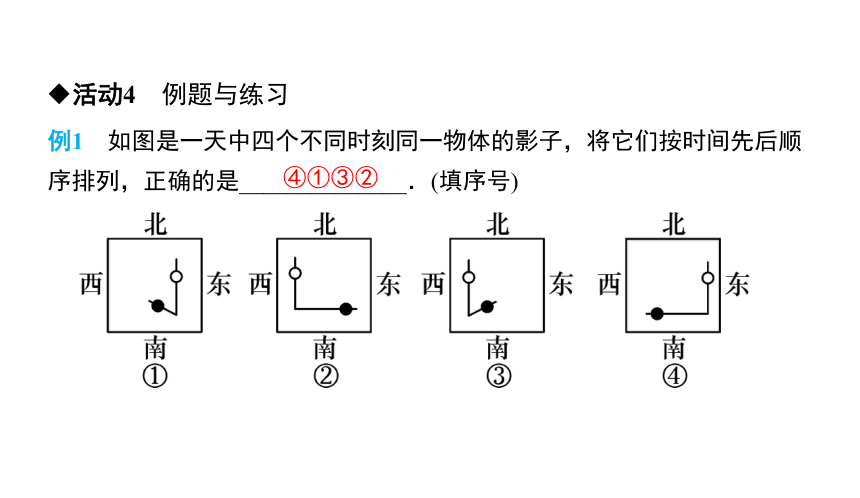
例1 如图是一天中四个不同时刻同一物体的影子,将它们按时间先后顺序排列,正确的是______________.(填序号)
④①③②
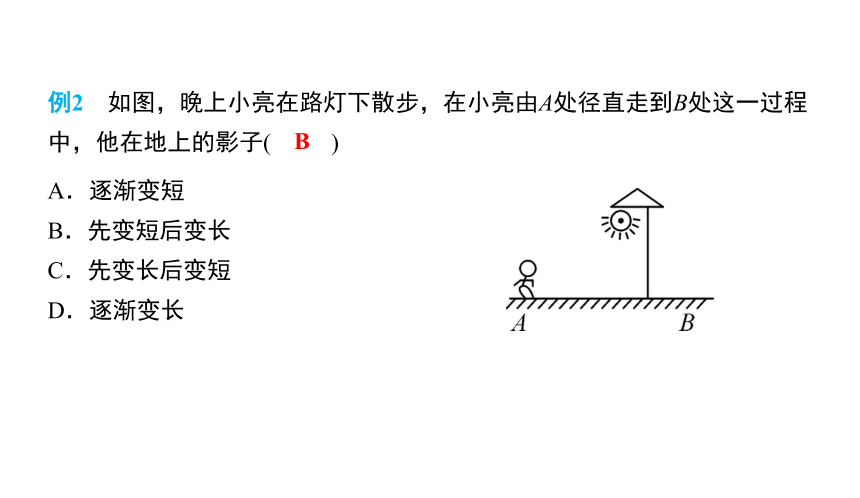
例2 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
A.逐渐变短
B.先变短后变长
C.先变长后变短
D.逐渐变长
B
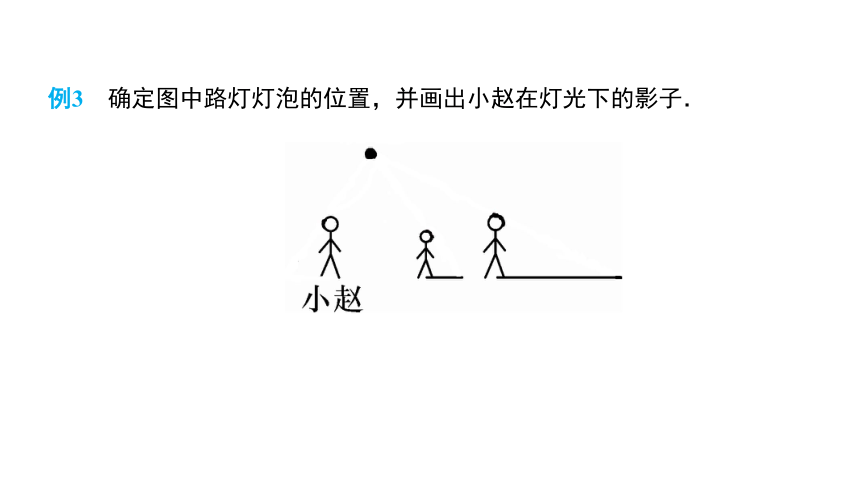
例3 确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
练 习
1.教材P88练习.
2.已知小明同学的身高为1.5 m,经太阳光照射,在地面上的影子长为2 m.若此时测得一塔在同一地面上的影子长为60 m,则塔高应为( )
A.90 m B.80 m C.45 m D.40 m
3.春蕾数学兴趣小组用一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影可能是_____________________________.(写出符合条件的两个图形即可)
C
平行四边形、矩形(答案不唯一)
练 习
4.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他的影子的顶部刚好接触到路灯AC的底部,当他向前再步行20 m到达点Q时,发现身前他的影子的顶部刚好接触到路灯BD的底部.已知丁轩同学的身高是1.5 m,两个路灯的高度都是9 m,则两路灯之间的距离是多少?
解:易得△BNQ≌△AMP.设AP=BQ=x m,则AB=(2x+20)m.由△BNQ∽△BCA,
解得x=5.
答:两路灯之间的距离为30 m.
∴2x+20=30(m).
人教版数学九年级下册
第29章 投影与视图
29.1 投影
第2课时 正投影及其性质
一、教学目标
二、教学重难点
重点
难点
1.了解正投影的概念,能根据正投影的性质画出简单平面图形的正投影.
2.经历观察、探究、思考、归纳的过程,掌握正投影的特征.
3.培养抽象、概括能力,发展空间想象能力.
正投影的含义及其性质.
归纳正投影的性质,正确画出简单平面图形的正投影.
活动1 新课导入
三、教学设计
如图表示一块三角尺在光线照射下形成的投影.其中哪些是中心投影,哪些是平行投影?图(2)(3)的投影线与投影面的位置关系有什么区别?
解:(1)是中心投影,(2)(3)是平行投影;
(2)的投影线与投影面不垂直,(3)的投影线与投影面垂直.
活动2 探究新知
1.教材P89第1个探究.
提出问题:三种情形下铁丝的正投影各是什么形状?大小有什么关系?
(1)当线段AB平行于投影面时,它的正投影是线段A1B1,它们的大小关系为_____________;
(2)当线段AB倾斜于投影面时,它的正投影是线段A2B2,它们的大小关系为______________;
(3)当线段AB垂直于投影面时,它的正投影是_________.
AB=A1B1
AB>A2B2
点A3(B3)
2.教材P89第2个探究.
提出问题:三种情形下纸板的正投影各是什么形状?大小有什么关系?
(1)当纸板P平行于投影面时,P的正投影与P的形状、大小________;
(2)当纸板P倾斜于投影面时,P的正投影与P的形状、大小________;
(3)当纸板P垂直于投影面时,P的正投影成为________.
相同
不同
线段
活动3 知识归纳
投影线________于投影面产生的投影叫做正投影.
(1)当线段平行于投影面时,线段与它的正投影的大小关系为________;
(2)当线段倾斜于投影面时,线段与它的正投影的大小关系为______________;
(3)当线段垂直于投影面时,它的正投影是__________.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小________.
垂直
相等
线段大于影长
一个点
一样
活动4 例题与练习
画出如图摆放的正方体在投影面P上的正投影.
(1)正方体的一个面ABCD平行于投影面P
(2)正方体的一个面ABCD倾斜于投影面P,上底面ADEF垂直于投影面P,并且上底面的对角线AE垂直于投影面P.
A
B
C
D
A
B
C
F
G
D
H
E
例1 教材P90例题.
分析:(1)当正方体在如图的位置时,正方体的一个面ABCD及与其相对的另一面与投影面平行,这两个面的正投影是与正方体的一个面的形状、大小完全相同的正方形A ' B ' C ' D ' .正方形A ' B ' C ' D '的四条边分别是正方体其余四个面(这些面垂直于投影面)的投影.因此,正方体的正投影是一个正方形.
(2)当正方体在如图的位置时,它的面ABCD和面ABGF倾斜于投影面,它们的投影分别是矩形A ' B ' C ' D '和A ' B ' G ' F ' ;正方体其余两个侧
面的投影也分别是上述矩形;上、下底面的投影分别是线段D ' F '和
C ' G ' .因此,正方体的投影是矩形F ' G ' C ' D ' ,其中线段A ' B '把矩形一分为二.
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'
B'
C'
D'
E
F
G
F'
G'
(2)如图,正方体的正投影为矩形F ' G ' C ' D ' ,这个矩形的长等于正方体的底面对角线长,矩形的宽等于正方体的棱长.矩形上、下两边中点连线A ' B '是正方体的侧棱AB及它所对的另一条侧棱EH的投影.
解: (1)如图,正方体的正投影为正方形A ' B ' C ' D ' ,它与正方体的一个面是全等关系.
H
例2 下列投影中,正投影是____________.(填序号)
③④⑤
例3 如图,已知线段AB=2 cm,投影面为P,太阳光线与地面垂直.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图②),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图③中画出线段AB的正投影,并求出其正投影的长.
解:(1)如图①,点C即为所求作的正投影;
(2)如图②,线段CD即为所求作的正投影,CD=2 cm;
(3)如图③,线段CD即为所求作的正投影,CD=2cos 30°= (cm).
练 习
1.教材P92练习.
2.当棱长为20 cm的正方体的某个面平行于投影面时,这个面的正投影的面积为( )
A.20 cm2 B.300 cm2 C.400 cm2 D.600 cm2
3.圆柱的上底面平行于投影面,则圆柱的正投影是______;长方体的前面是个长方形,且前面平行于投影面,则长方体的正投影是_________.
C
圆
长方形
练 习
4.一个圆锥的轴截面平行于投影面,圆锥的正投影是边长为2的正三角形.
(1)求圆锥的体积;
(2)求圆锥的表面积.
解:由正投影可得,圆锥的底面直径为2,
∴r=1,高h= ,
(2)l=2,∴S表=πr2+πrl=π×12+π×1×2=3π.
谢谢观看
人教版数学九年级下册
第29章 投影与视图
29.1 投影
第1课时 平行投影与中心投影
一、教学目标
二、教学重难点
重点
难点
1.经历实践探索,了解投影、平行投影与中心投影的概念.
2.了解平行投影与中心投影的区别.
3.学会关注生活中有关投影的数学问题,提高数学应用意识.
理解投影的概念.
掌握中心投影与平行投影的联系与区别.
活动1 新课导入
三、教学设计
感受日常生活中的一些投影现象.
活动2 探究新知
1.教材P87部分内容.
提出问题:
(1)什么叫投影?什么叫投影线?什么叫投影面?
(2)什么叫平行投影?
(3)请例举生活中平行投影的例子.
2.教材P88练习以上部分.
提出问题:
(1)什么叫中心投影?请例举一些中心投影的例子;
(2)平行投影和中心投影的区别是什么?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.用_______照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,____________叫做投影线,________所在的平面叫做投影面.
2.由__________形成的投影叫做平行投影,由________ (点光源)发出的光线形成的投影叫做中心投影.
光线
照射光线
投影
平行光线
同一点
活动4 例题与练习
例1 如图是一天中四个不同时刻同一物体的影子,将它们按时间先后顺序排列,正确的是______________.(填序号)
④①③②
例2 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
A.逐渐变短
B.先变短后变长
C.先变长后变短
D.逐渐变长
B
例3 确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
练 习
1.教材P88练习.
2.已知小明同学的身高为1.5 m,经太阳光照射,在地面上的影子长为2 m.若此时测得一塔在同一地面上的影子长为60 m,则塔高应为( )
A.90 m B.80 m C.45 m D.40 m
3.春蕾数学兴趣小组用一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影可能是_____________________________.(写出符合条件的两个图形即可)
C
平行四边形、矩形(答案不唯一)
练 习
4.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他的影子的顶部刚好接触到路灯AC的底部,当他向前再步行20 m到达点Q时,发现身前他的影子的顶部刚好接触到路灯BD的底部.已知丁轩同学的身高是1.5 m,两个路灯的高度都是9 m,则两路灯之间的距离是多少?
解:易得△BNQ≌△AMP.设AP=BQ=x m,则AB=(2x+20)m.由△BNQ∽△BCA,
解得x=5.
答:两路灯之间的距离为30 m.
∴2x+20=30(m).
人教版数学九年级下册
第29章 投影与视图
29.1 投影
第2课时 正投影及其性质
一、教学目标
二、教学重难点
重点
难点
1.了解正投影的概念,能根据正投影的性质画出简单平面图形的正投影.
2.经历观察、探究、思考、归纳的过程,掌握正投影的特征.
3.培养抽象、概括能力,发展空间想象能力.
正投影的含义及其性质.
归纳正投影的性质,正确画出简单平面图形的正投影.
活动1 新课导入
三、教学设计
如图表示一块三角尺在光线照射下形成的投影.其中哪些是中心投影,哪些是平行投影?图(2)(3)的投影线与投影面的位置关系有什么区别?
解:(1)是中心投影,(2)(3)是平行投影;
(2)的投影线与投影面不垂直,(3)的投影线与投影面垂直.
活动2 探究新知
1.教材P89第1个探究.
提出问题:三种情形下铁丝的正投影各是什么形状?大小有什么关系?
(1)当线段AB平行于投影面时,它的正投影是线段A1B1,它们的大小关系为_____________;
(2)当线段AB倾斜于投影面时,它的正投影是线段A2B2,它们的大小关系为______________;
(3)当线段AB垂直于投影面时,它的正投影是_________.
AB=A1B1
AB>A2B2
点A3(B3)
2.教材P89第2个探究.
提出问题:三种情形下纸板的正投影各是什么形状?大小有什么关系?
(1)当纸板P平行于投影面时,P的正投影与P的形状、大小________;
(2)当纸板P倾斜于投影面时,P的正投影与P的形状、大小________;
(3)当纸板P垂直于投影面时,P的正投影成为________.
相同
不同
线段
活动3 知识归纳
投影线________于投影面产生的投影叫做正投影.
(1)当线段平行于投影面时,线段与它的正投影的大小关系为________;
(2)当线段倾斜于投影面时,线段与它的正投影的大小关系为______________;
(3)当线段垂直于投影面时,它的正投影是__________.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小________.
垂直
相等
线段大于影长
一个点
一样
活动4 例题与练习
画出如图摆放的正方体在投影面P上的正投影.
(1)正方体的一个面ABCD平行于投影面P
(2)正方体的一个面ABCD倾斜于投影面P,上底面ADEF垂直于投影面P,并且上底面的对角线AE垂直于投影面P.
A
B
C
D
A
B
C
F
G
D
H
E
例1 教材P90例题.
分析:(1)当正方体在如图的位置时,正方体的一个面ABCD及与其相对的另一面与投影面平行,这两个面的正投影是与正方体的一个面的形状、大小完全相同的正方形A ' B ' C ' D ' .正方形A ' B ' C ' D '的四条边分别是正方体其余四个面(这些面垂直于投影面)的投影.因此,正方体的正投影是一个正方形.
(2)当正方体在如图的位置时,它的面ABCD和面ABGF倾斜于投影面,它们的投影分别是矩形A ' B ' C ' D '和A ' B ' G ' F ' ;正方体其余两个侧
面的投影也分别是上述矩形;上、下底面的投影分别是线段D ' F '和
C ' G ' .因此,正方体的投影是矩形F ' G ' C ' D ' ,其中线段A ' B '把矩形一分为二.
A
B
C
D
A'
B'
C'
D'
A
B
C
D
A'
B'
C'
D'
E
F
G
F'
G'
(2)如图,正方体的正投影为矩形F ' G ' C ' D ' ,这个矩形的长等于正方体的底面对角线长,矩形的宽等于正方体的棱长.矩形上、下两边中点连线A ' B '是正方体的侧棱AB及它所对的另一条侧棱EH的投影.
解: (1)如图,正方体的正投影为正方形A ' B ' C ' D ' ,它与正方体的一个面是全等关系.
H
例2 下列投影中,正投影是____________.(填序号)
③④⑤
例3 如图,已知线段AB=2 cm,投影面为P,太阳光线与地面垂直.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图②),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图③中画出线段AB的正投影,并求出其正投影的长.
解:(1)如图①,点C即为所求作的正投影;
(2)如图②,线段CD即为所求作的正投影,CD=2 cm;
(3)如图③,线段CD即为所求作的正投影,CD=2cos 30°= (cm).
练 习
1.教材P92练习.
2.当棱长为20 cm的正方体的某个面平行于投影面时,这个面的正投影的面积为( )
A.20 cm2 B.300 cm2 C.400 cm2 D.600 cm2
3.圆柱的上底面平行于投影面,则圆柱的正投影是______;长方体的前面是个长方形,且前面平行于投影面,则长方体的正投影是_________.
C
圆
长方形
练 习
4.一个圆锥的轴截面平行于投影面,圆锥的正投影是边长为2的正三角形.
(1)求圆锥的体积;
(2)求圆锥的表面积.
解:由正投影可得,圆锥的底面直径为2,
∴r=1,高h= ,
(2)l=2,∴S表=πr2+πrl=π×12+π×1×2=3π.
谢谢观看
