28.1 锐角三角函数 课件 2023-2024学年人教版数学九年级下册(共4课时)
文档属性
| 名称 | 28.1 锐角三角函数 课件 2023-2024学年人教版数学九年级下册(共4课时) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 10:42:38 | ||
图片预览










文档简介
(共51张PPT)
人教版数学九年级下册
第28章 锐角三角函数
28.1 锐角三角函数
第1课时 锐角的正弦
一、教学目标
二、教学重难点
重点
难点
1.理解锐角正弦的概念,能够运用sin A表示直角三角形两边的比值及进行简单的计算.
2.体会数形结合思想在解决数学问题中的广泛应用.
理解锐角正弦sin A的意义,能用它进行简单的计算.
领悟正弦的概念.
活动1 新课导入
三、教学设计
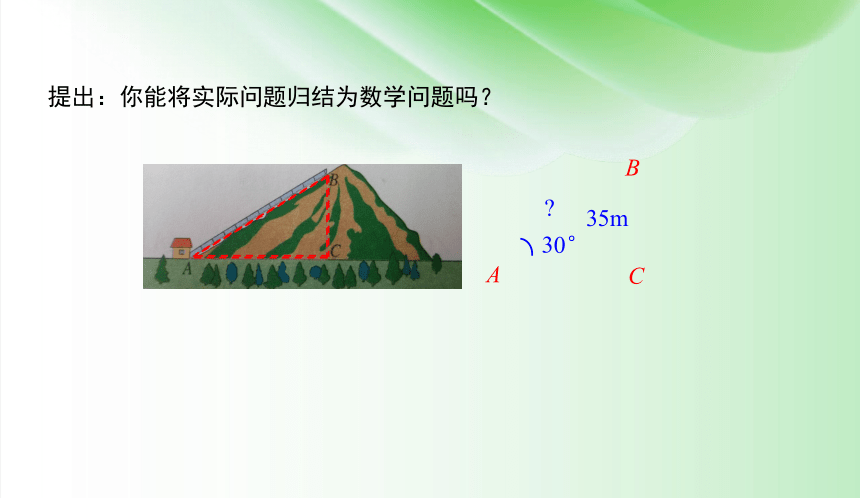
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上建一座扬水站,对坡面绿地进行喷灌.先测得斜坡的坡脚(∠A)为30°,为使出水口的高度为35m,需要准备多长的水管?
提出:你能将实际问题归结为数学问题吗?
A
B
C
30°
35m
A
B
C
30°
35m
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB.
在直角三角形中,30°的角所对的边等于斜边的一半
所以AB=2BC=70m.
如果出水的高度为50m,那么需要准备多长的水管?
活动2 探究新知
思考完成并交流展示.
1.教材P61问题.
提出问题:
(1)问题中是根据什么求出水管长度的?
(2)如果出水口的高度是40 m时,需要准备多长的水管?
(3)如果出水口的高度是a m时,需要准备多长的水管?你从中发现了什么规律?
(4)教材P61第1个思考,由此你能得出什么结论?
2.教材P61第2个思考.
提出问题:
(1)已知条件是什么?要求的是什么?我们可以根据什么定理来求解?根据勾股定理,你列出的等式是什么? 的值与三角形的大小有关系吗?由此,你能得出什么结论?
(2)在上面求AB(所需水管的长度)和∠A的对边与斜边的比 的过程中,你能得出什么结论?可以相互交流.
(3)当∠A是任意一个确定的锐角时,它的对边与斜边的比是否也是一个固定值呢?
3.教材P62探究.
活动3 知识归纳
1.在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的对边与斜边的比都是一个________.
固定值
2.如图,在Rt△ABC中,∠C=90°,我们把锐角A的______________叫做∠A的正弦,记作sin A,即sin A=____.
对边与斜边的比
活动4 例题与练习
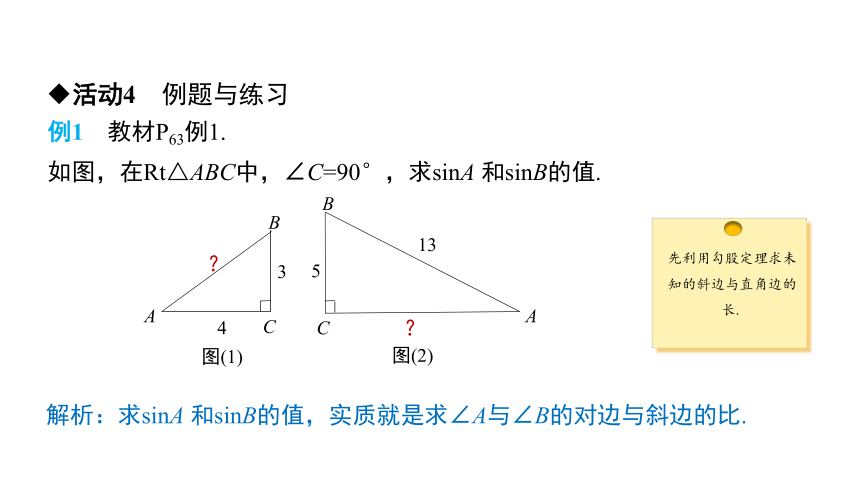
如图,在Rt△ABC中,∠C=90°,求sinA 和sinB的值.
A
A
B
B
C
C
4
3
13
5
图(1)
图(2)
解析:求sinA 和sinB的值,实质就是求∠A与∠B的对边与斜边的比.
?
?
例1 教材P63例1.
先利用勾股定理求未知的斜边与直角边的长.
解:如图(1),在Rt△ABC中,由勾股定理得
因此
如图(2),在Rt△ABC中,由勾股定理得
因此
A
A
B
B
C
C
4
3
13
5
图(1)
图(2)
?
?
例2 如图,在矩形ABCD中,DE⊥AC于点E.设∠ADE=α且sin α= ,AB=4,求AD的长.
解:∵∠ADE+∠DAC=90°,∠DAC+∠BAC=90°,
∴∠ADE=∠BAC,
设AC=5x,BC=4x,则AB=3x=4,
例3 如图,⊙O是△ABC的外接圆,AD是⊙O的直径.若⊙O的半径
为 ,AC=2,求sin B的值.
解:连接CD.
∵AD是⊙O的直径,
∴∠ACD=90°,
由圆周角定理,得∠B=∠D,
练 习
1.教材P64练习第1题.
2.如图,在⊙O中过直径AB延长线上的点C作⊙O的一条切线,切点为D.若AC=7,AB=4,则sin C的值为_____.
练 习
3.如图,把含30°角的三角尺ABC绕点B按逆时针方向旋转90°到三角尺DBE的位置,连接AD,求sin ∠ADE的值.
解:过点E作EF⊥AD于点F.
设BD=x.由旋转的性质,
得∠ABD=90°,AB=BD=x,∠EDB=30°,
∴∠DAB=45°,AD=x.
∵∠AFE=90°,∠DAB=45°,
∴△AEF是等腰直角三角形,
人教版数学九年级下册
第28章 锐角三角函数
28.1 锐角三角函数
第2课时 锐角的余弦和正切
一、教学目标
二、教学重难点
重点
难点
1.理解余弦、正切的概念,了解锐角三角函数的定义.
2.能运用余弦、正切的定义解决问题.
理解锐角三角函数的意义,用它们进行简单的计算.
以函数的角度理解正弦、余弦、正切.
活动1 新课导入
三、教学设计
1.sin 30°=____,sin 45°=____.
2.在Rt△ABC中,各边的长度都扩大为原来的3倍,那么锐角∠A的正弦值______.
3.在Rt△ABC中,∠C=90°,BC=2, sinA= ,则AC的长为____.
不变
活动2 探究新知
1.教材P64探究.
2.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠A′.
(2)当∠A确定后,∠A的邻边与斜边的比确定吗?它的对边与邻边的比呢?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.在Rt△ABC中,∠C=90°,锐角A的____边与____边的比,叫做∠A的余弦,记作_______,即cos A=____.
2.在Rt△ABC中,∠C=90°,锐角A的____边与____边的比,叫做∠A的正切,记作________,即tan A=_____.
3.锐角A的______、______、______都叫做∠A的三角函数值.
邻
斜
cosA
对
邻
tanA
正弦
余弦
正切
活动4 例题与练习
如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
因此
例1 教材P65例2.
例2 如图,在Rt△ABC中,∠C=90°,tan A= ,求sin A和cos A的值.
例3 已知关于x的方程x2-5x·sin α+1=0的一个根为2+ ,且α为锐角,求cos α.
解:设方程的另一个根为x2,则(2+ )x2=1,
∴x2=2- .
根据根与系数的关系,得5sin α=(2+ )+(2- ),解得sin α= .
设锐角α所在的直角三角形的对边长为4k(k>0),则斜边长为5k,邻边长为3k,
练 习
1.教材P65练习第1,2题.
2.如图,点A为∠α边上的任意一点,过点A作AC⊥BC于点C,过点C作CD⊥AB于点D,下列用线段比表示cos α的值,错误的是( )
C
练 习
3.如图,在Rt△ABC中,CA=CB,AB=9 ,点D在边BC上,连接AD.若tan ∠CAD= ,则BD的长为____.
6
4.如图,在Rt△ABC中,∠C=90°,D是边BC上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个三角函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
解:(1)在Rt△ADC中,由勾股定理,得AD=3 ,
人教版数学九年级下册
第28章 锐角三角函数
28.1 锐角三角函数
第3课时 特殊角的三角函数值
一、教学目标
1.掌握30°,45°,60°角的三角函数值,能够用它们进行计算.
2.能够根据30°,45°,60°角的三角函数值,求出相应锐角的大小.
3.经历探索30°,45°,60°角的三角函数值的过程,并能进行有关的推理.
二、教学重难点
重点
难点
掌握30°,45°,60°角的三角函数值,能够用它们进行计算.
理解30°,45°,60°角的三角函数值的探索过程.
活动1 新课导入
三、教学设计
在前面我们已经得到sin 30°= ,sin 45°= ,你能得到30°,45°角的其他三角函数值吗?不妨试试看.
活动2 探究新知
思考完成并交流展示.
教材P65探究.
提出问题:
(1) 两块三角尺(如图)有几个不同的锐角?这几个锐角分别是多少度?
(2)还记得我们推导正弦关系的时候所得到的结论吗?你能推导出sin 60°的值以及30°,45°,60°角的其他三角函数值吗?
(3)如图,分别在含30°和45°角的直角三角形中,设较短边长为1,利用勾股定理和三角函数定义填空:
①sin 30°= ,sin 45°= ,sin 60°= ;
②cos 30°= ,cos 45°= ,cos 60°= ;
③tan 30°= ,tan 45°= ,tan 60°= .
1
活动3 知识归纳
30°,45°,60°角的正弦值、余弦值和正切值如下表:
锐角a 三角函数 30° 45° 60°
sin a
cos a
tan a
活动4 例题与练习
求下列各式的值:
解:
例1 教材P66例3.
sin260°表示(sin60°)2,即(sin60°)×(sin60°).
(1)如图,在Rt△ABC中,∠C=90°, ,求∠A的度数;
解: 在图中,
A
B
C
例2 教材P66例4.
解: 在图中,
A
B
O
(2)如图,AO是圆锥的高,OB是底面半径,AO= OB, 求 a 的度数.
例3 如图,在△ABC中,∠ABC=90°,∠A=30°,D是边AB上一点,∠BDC=45°,AD=4,求BC的长.
解:∵∠B=90°,∠BDC=45°,
∴BD=BC.在Rt△ABC中,
∴△BCD为等腰直角三角形,
练 习
1.教材P67练习第1,2题.
2.点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )
B
练 习
3.计算:
人教版数学九年级下册
第28章 锐角三角函数
28.1 锐角三角函数
第4课时 用计算器求三角函数值和锐角度数
一、教学目标
二、教学重难点
重点
难点
掌握用计算器求锐角三角函数值以及已知一个锐角的某一三角函数值,利用计算器求出这个锐角的度数的方法.
运用计算器求锐角三角函数值或锐角.
用计算器进行有关直角三角形的计算.
活动1 新课导入
三、教学设计
1.计算:cos 30°·sin 30°=____,
tan 60°=____,
cos2 45°+tan 30°·sin 60°=____.
2.当锐角A是30°,45°,60°时,可以求出这些角的正弦、余弦、正切值,当锐角A不是这些特殊值时,怎样得到它的三角函数值?
1
活动2 探究新知
1.教材P67练习下面部分内容.
提出问题:
(2)利用计算器完成下表:
按键顺序 显示结果
sin 67°38′24″
tan 63°27′
cos 18°59′27″
0.924 811 845
2.001 314 153
0.945 570 65
2.教材P68上面部分内容.
提出问题:
(1)请注意计算器上的 键,它有什么作用?
(2)已知sin A=0.501 8,用计算器求锐角A的按键顺序是什么?已知cos A=0.625 2,tan A=3.741 6,求锐角A时按键顺序又分别是什么呢?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.由锐角求三角函数值的按键顺序为:接要求先按功能键 或
或 ,再输入 .
2.由三角函数值求锐角的按键顺序为:先按 键,然后再按
或 或 ,再输入数值,得到的结果为 的形式.
角度
度数
3.锐角α的____________值随α的增大而增大;锐角α的______值随α的增大而减小.
正弦和正切
余弦
活动4 例题与练习
例1 利用科学计算器计算 cos 55°,按键顺序正确的是( )
√
√
√
√
C
例2 如图,请根据图示数据,计算角α(精确到1′).
解:∵FG=83-(150-124)=57,
∴锐角α≈22°9′.
例3 如图,某校自行车车棚的人字架顶棚为等腰三角形,D是AB的中点,中柱CD=1 m,∠A=27°,求跨度AB的长.(精确到0.1 m)
∴AB=2AD≈3.9(m).
练 习
1.教材P68练习第1,2题.
2.已知tan α=0.324 9,则α约为( )
A.17° B.18° C.38° D.39°
3.下列各式一定成立的是( )
A.tan 78°>tan 52°>tan 23°
B.sin 70°C.cos 70°>cos 50°>cos 24°
D.tan 65°B
A
练 习
4.如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,且AD=6,BD=3,求∠C的度数.(精确到1′)
∴∠C≈71°34′.
得锐角∠B≈63°26′,
谢谢观看
人教版数学九年级下册
第28章 锐角三角函数
28.1 锐角三角函数
第1课时 锐角的正弦
一、教学目标
二、教学重难点
重点
难点
1.理解锐角正弦的概念,能够运用sin A表示直角三角形两边的比值及进行简单的计算.
2.体会数形结合思想在解决数学问题中的广泛应用.
理解锐角正弦sin A的意义,能用它进行简单的计算.
领悟正弦的概念.
活动1 新课导入
三、教学设计
为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上建一座扬水站,对坡面绿地进行喷灌.先测得斜坡的坡脚(∠A)为30°,为使出水口的高度为35m,需要准备多长的水管?
提出:你能将实际问题归结为数学问题吗?
A
B
C
30°
35m
A
B
C
30°
35m
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB.
在直角三角形中,30°的角所对的边等于斜边的一半
所以AB=2BC=70m.
如果出水的高度为50m,那么需要准备多长的水管?
活动2 探究新知
思考完成并交流展示.
1.教材P61问题.
提出问题:
(1)问题中是根据什么求出水管长度的?
(2)如果出水口的高度是40 m时,需要准备多长的水管?
(3)如果出水口的高度是a m时,需要准备多长的水管?你从中发现了什么规律?
(4)教材P61第1个思考,由此你能得出什么结论?
2.教材P61第2个思考.
提出问题:
(1)已知条件是什么?要求的是什么?我们可以根据什么定理来求解?根据勾股定理,你列出的等式是什么? 的值与三角形的大小有关系吗?由此,你能得出什么结论?
(2)在上面求AB(所需水管的长度)和∠A的对边与斜边的比 的过程中,你能得出什么结论?可以相互交流.
(3)当∠A是任意一个确定的锐角时,它的对边与斜边的比是否也是一个固定值呢?
3.教材P62探究.
活动3 知识归纳
1.在Rt△ABC中,当锐角A的度数一定时,无论这个直角三角形大小如何,∠A的对边与斜边的比都是一个________.
固定值
2.如图,在Rt△ABC中,∠C=90°,我们把锐角A的______________叫做∠A的正弦,记作sin A,即sin A=____.
对边与斜边的比
活动4 例题与练习
如图,在Rt△ABC中,∠C=90°,求sinA 和sinB的值.
A
A
B
B
C
C
4
3
13
5
图(1)
图(2)
解析:求sinA 和sinB的值,实质就是求∠A与∠B的对边与斜边的比.
?
?
例1 教材P63例1.
先利用勾股定理求未知的斜边与直角边的长.
解:如图(1),在Rt△ABC中,由勾股定理得
因此
如图(2),在Rt△ABC中,由勾股定理得
因此
A
A
B
B
C
C
4
3
13
5
图(1)
图(2)
?
?
例2 如图,在矩形ABCD中,DE⊥AC于点E.设∠ADE=α且sin α= ,AB=4,求AD的长.
解:∵∠ADE+∠DAC=90°,∠DAC+∠BAC=90°,
∴∠ADE=∠BAC,
设AC=5x,BC=4x,则AB=3x=4,
例3 如图,⊙O是△ABC的外接圆,AD是⊙O的直径.若⊙O的半径
为 ,AC=2,求sin B的值.
解:连接CD.
∵AD是⊙O的直径,
∴∠ACD=90°,
由圆周角定理,得∠B=∠D,
练 习
1.教材P64练习第1题.
2.如图,在⊙O中过直径AB延长线上的点C作⊙O的一条切线,切点为D.若AC=7,AB=4,则sin C的值为_____.
练 习
3.如图,把含30°角的三角尺ABC绕点B按逆时针方向旋转90°到三角尺DBE的位置,连接AD,求sin ∠ADE的值.
解:过点E作EF⊥AD于点F.
设BD=x.由旋转的性质,
得∠ABD=90°,AB=BD=x,∠EDB=30°,
∴∠DAB=45°,AD=x.
∵∠AFE=90°,∠DAB=45°,
∴△AEF是等腰直角三角形,
人教版数学九年级下册
第28章 锐角三角函数
28.1 锐角三角函数
第2课时 锐角的余弦和正切
一、教学目标
二、教学重难点
重点
难点
1.理解余弦、正切的概念,了解锐角三角函数的定义.
2.能运用余弦、正切的定义解决问题.
理解锐角三角函数的意义,用它们进行简单的计算.
以函数的角度理解正弦、余弦、正切.
活动1 新课导入
三、教学设计
1.sin 30°=____,sin 45°=____.
2.在Rt△ABC中,各边的长度都扩大为原来的3倍,那么锐角∠A的正弦值______.
3.在Rt△ABC中,∠C=90°,BC=2, sinA= ,则AC的长为____.
不变
活动2 探究新知
1.教材P64探究.
2.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠A′.
(2)当∠A确定后,∠A的邻边与斜边的比确定吗?它的对边与邻边的比呢?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.在Rt△ABC中,∠C=90°,锐角A的____边与____边的比,叫做∠A的余弦,记作_______,即cos A=____.
2.在Rt△ABC中,∠C=90°,锐角A的____边与____边的比,叫做∠A的正切,记作________,即tan A=_____.
3.锐角A的______、______、______都叫做∠A的三角函数值.
邻
斜
cosA
对
邻
tanA
正弦
余弦
正切
活动4 例题与练习
如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
因此
例1 教材P65例2.
例2 如图,在Rt△ABC中,∠C=90°,tan A= ,求sin A和cos A的值.
例3 已知关于x的方程x2-5x·sin α+1=0的一个根为2+ ,且α为锐角,求cos α.
解:设方程的另一个根为x2,则(2+ )x2=1,
∴x2=2- .
根据根与系数的关系,得5sin α=(2+ )+(2- ),解得sin α= .
设锐角α所在的直角三角形的对边长为4k(k>0),则斜边长为5k,邻边长为3k,
练 习
1.教材P65练习第1,2题.
2.如图,点A为∠α边上的任意一点,过点A作AC⊥BC于点C,过点C作CD⊥AB于点D,下列用线段比表示cos α的值,错误的是( )
C
练 习
3.如图,在Rt△ABC中,CA=CB,AB=9 ,点D在边BC上,连接AD.若tan ∠CAD= ,则BD的长为____.
6
4.如图,在Rt△ABC中,∠C=90°,D是边BC上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个三角函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
解:(1)在Rt△ADC中,由勾股定理,得AD=3 ,
人教版数学九年级下册
第28章 锐角三角函数
28.1 锐角三角函数
第3课时 特殊角的三角函数值
一、教学目标
1.掌握30°,45°,60°角的三角函数值,能够用它们进行计算.
2.能够根据30°,45°,60°角的三角函数值,求出相应锐角的大小.
3.经历探索30°,45°,60°角的三角函数值的过程,并能进行有关的推理.
二、教学重难点
重点
难点
掌握30°,45°,60°角的三角函数值,能够用它们进行计算.
理解30°,45°,60°角的三角函数值的探索过程.
活动1 新课导入
三、教学设计
在前面我们已经得到sin 30°= ,sin 45°= ,你能得到30°,45°角的其他三角函数值吗?不妨试试看.
活动2 探究新知
思考完成并交流展示.
教材P65探究.
提出问题:
(1) 两块三角尺(如图)有几个不同的锐角?这几个锐角分别是多少度?
(2)还记得我们推导正弦关系的时候所得到的结论吗?你能推导出sin 60°的值以及30°,45°,60°角的其他三角函数值吗?
(3)如图,分别在含30°和45°角的直角三角形中,设较短边长为1,利用勾股定理和三角函数定义填空:
①sin 30°= ,sin 45°= ,sin 60°= ;
②cos 30°= ,cos 45°= ,cos 60°= ;
③tan 30°= ,tan 45°= ,tan 60°= .
1
活动3 知识归纳
30°,45°,60°角的正弦值、余弦值和正切值如下表:
锐角a 三角函数 30° 45° 60°
sin a
cos a
tan a
活动4 例题与练习
求下列各式的值:
解:
例1 教材P66例3.
sin260°表示(sin60°)2,即(sin60°)×(sin60°).
(1)如图,在Rt△ABC中,∠C=90°, ,求∠A的度数;
解: 在图中,
A
B
C
例2 教材P66例4.
解: 在图中,
A
B
O
(2)如图,AO是圆锥的高,OB是底面半径,AO= OB, 求 a 的度数.
例3 如图,在△ABC中,∠ABC=90°,∠A=30°,D是边AB上一点,∠BDC=45°,AD=4,求BC的长.
解:∵∠B=90°,∠BDC=45°,
∴BD=BC.在Rt△ABC中,
∴△BCD为等腰直角三角形,
练 习
1.教材P67练习第1,2题.
2.点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )
B
练 习
3.计算:
人教版数学九年级下册
第28章 锐角三角函数
28.1 锐角三角函数
第4课时 用计算器求三角函数值和锐角度数
一、教学目标
二、教学重难点
重点
难点
掌握用计算器求锐角三角函数值以及已知一个锐角的某一三角函数值,利用计算器求出这个锐角的度数的方法.
运用计算器求锐角三角函数值或锐角.
用计算器进行有关直角三角形的计算.
活动1 新课导入
三、教学设计
1.计算:cos 30°·sin 30°=____,
tan 60°=____,
cos2 45°+tan 30°·sin 60°=____.
2.当锐角A是30°,45°,60°时,可以求出这些角的正弦、余弦、正切值,当锐角A不是这些特殊值时,怎样得到它的三角函数值?
1
活动2 探究新知
1.教材P67练习下面部分内容.
提出问题:
(2)利用计算器完成下表:
按键顺序 显示结果
sin 67°38′24″
tan 63°27′
cos 18°59′27″
0.924 811 845
2.001 314 153
0.945 570 65
2.教材P68上面部分内容.
提出问题:
(1)请注意计算器上的 键,它有什么作用?
(2)已知sin A=0.501 8,用计算器求锐角A的按键顺序是什么?已知cos A=0.625 2,tan A=3.741 6,求锐角A时按键顺序又分别是什么呢?
分析答案,提出疑惑,共同解决.
活动3 知识归纳
1.由锐角求三角函数值的按键顺序为:接要求先按功能键 或
或 ,再输入 .
2.由三角函数值求锐角的按键顺序为:先按 键,然后再按
或 或 ,再输入数值,得到的结果为 的形式.
角度
度数
3.锐角α的____________值随α的增大而增大;锐角α的______值随α的增大而减小.
正弦和正切
余弦
活动4 例题与练习
例1 利用科学计算器计算 cos 55°,按键顺序正确的是( )
√
√
√
√
C
例2 如图,请根据图示数据,计算角α(精确到1′).
解:∵FG=83-(150-124)=57,
∴锐角α≈22°9′.
例3 如图,某校自行车车棚的人字架顶棚为等腰三角形,D是AB的中点,中柱CD=1 m,∠A=27°,求跨度AB的长.(精确到0.1 m)
∴AB=2AD≈3.9(m).
练 习
1.教材P68练习第1,2题.
2.已知tan α=0.324 9,则α约为( )
A.17° B.18° C.38° D.39°
3.下列各式一定成立的是( )
A.tan 78°>tan 52°>tan 23°
B.sin 70°
D.tan 65°
A
练 习
4.如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,且AD=6,BD=3,求∠C的度数.(精确到1′)
∴∠C≈71°34′.
得锐角∠B≈63°26′,
谢谢观看
