2023-2024学年人教版数学八年级下册16.1二次根式 课件(共24张PPT)
文档属性
| 名称 | 2023-2024学年人教版数学八年级下册16.1二次根式 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 659.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 12:48:49 | ||
图片预览







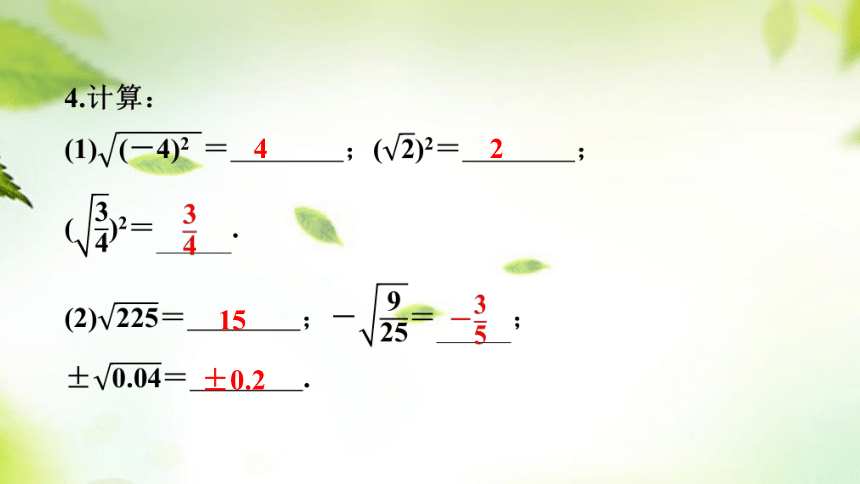

文档简介
(共24张PPT)
人教版八年级数学下册课件
课标要求
01
基础梳理
02
典例探究
03
课时训练
04
第十六章 二 次根式
16.1 二次根式
课标要求
了解二次根式的概念及性质.
基础梳理
1.知识储备:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.正数的平方根有两个,它们互为
,其中正的平方根就是这个数的算术平方根;0的平方根是0,0的算术平方根是0;负数没有平方根.
相反数
2.二次根式的概念: 形如 (a≥0)的式子叫做二次根式,“”称为二次根号.
3.二次根式的性质:
(1)()2= (a≥0).
(2)= =
(3)双重非负性: 0(a≥0).
a
≥
1.(1)一个数的平方是16,则这个数是 .
(2)7的平方根是 ;
13的算术平方根是 .
2.下列各式中是二次根式的是( )
A. B. C. D.(x<0)
±4
±
C
3.(人教八下P5改编)用代数式表示:面积为S的正方形的边长.
4.计算:
(1)= ;()2= ;
()2= .
(2)= ;-= ;
±= .
4
2
15
-
±0.2
知识点1 二次根式有意义的条件
【例题1】(2022·广州)代数式有意义时,x应满足的条件为( )
A.x≠-1 B.x>-1
C.x<-1 D.x≤-1
B
典例探究
【变式1】若式子有意义,则实数x的值可以是( )
A.0 B.1 C.2 D.5
A
知识点2 二次根式的性质
【例题2】已知0<x<2,化简.
解:∵0<x<2,∴x-2<0,x-3<0.
∴=2-x+3-x=5-2x.
【变式2】已知y=,求的值.
A组
1.二次根式的最小值为( )
A.0 B.1
C.-1 D.不能确定
A
课时训练
2.下列式子中不是代数式的为( )
A.(x≥-2) B.5a+8=7
C.2 020 D.(a≠)
B
3.若x=+2,则|x-y|的值是( )
A.5 B.1 C.-1 D.2
B
4.若等式=x-8成立,则x的取值范围是
.
5.若式子3+x(x-1)0有意义,则x的取值范围是
.
6.已知y=-2,则xy的值为 .
x≥8
x≤2且x≠1
7.计算:
(1) ; (2);
(3)(x<3);
(4)()-1-(-1)0+.
解:(1)原式=6.
(2)原式=9.
(3)∵x<3,∴x-3<0.
∴原式==3-x.
(4)原式=2-1+3=4.
B组
8.如果有y=-2,求xy的值.
解:由题意,得x2-16≥0,且16-x2≥0.解得x=±4.
∵4-x≠0,∴x≠4.
∴x=-4.∴y=-2.
∴xy=(-4)-2=.
9.已知y=+8.求-x-3y的立方根.
解:∵y=+8,
∴x-3≥0,且3-x≥0,
解得x=3,
∴y=8,
∴-x-3y=-3-24=-27,
∴-x-3y的立方根为-3.
10.已知0<a<1,试化简:
.
解:+4=a2-2++4=a2+2+,
-4=a2+2+-4=a2-2+.
∴原式=
=.
∵0<a<1,∴a+>0,a-<0.
∴原式=a++a-=2a.
11.请认真阅读下面例题的解法,并回答拓展题.
例:已知y=+2 022,求的值.
解:由解得x=2 021,
∴y=2 022,
∴.
拓展题:已知=b+8.
(1)求a和b的值;
(2)求a2-b2的平方根.
解:(1)由解得a=17,
∴b=-8,
∴a=17,b=-8;
(2)a2-b2=172-82=225,
∵225的平方根是±15,
∴a2-b2的平方根是±15.
谢谢大家欣赏
人教版八年级数学下册课件
课标要求
01
基础梳理
02
典例探究
03
课时训练
04
第十六章 二 次根式
16.1 二次根式
课标要求
了解二次根式的概念及性质.
基础梳理
1.知识储备:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.正数的平方根有两个,它们互为
,其中正的平方根就是这个数的算术平方根;0的平方根是0,0的算术平方根是0;负数没有平方根.
相反数
2.二次根式的概念: 形如 (a≥0)的式子叫做二次根式,“”称为二次根号.
3.二次根式的性质:
(1)()2= (a≥0).
(2)= =
(3)双重非负性: 0(a≥0).
a
≥
1.(1)一个数的平方是16,则这个数是 .
(2)7的平方根是 ;
13的算术平方根是 .
2.下列各式中是二次根式的是( )
A. B. C. D.(x<0)
±4
±
C
3.(人教八下P5改编)用代数式表示:面积为S的正方形的边长.
4.计算:
(1)= ;()2= ;
()2= .
(2)= ;-= ;
±= .
4
2
15
-
±0.2
知识点1 二次根式有意义的条件
【例题1】(2022·广州)代数式有意义时,x应满足的条件为( )
A.x≠-1 B.x>-1
C.x<-1 D.x≤-1
B
典例探究
【变式1】若式子有意义,则实数x的值可以是( )
A.0 B.1 C.2 D.5
A
知识点2 二次根式的性质
【例题2】已知0<x<2,化简.
解:∵0<x<2,∴x-2<0,x-3<0.
∴=2-x+3-x=5-2x.
【变式2】已知y=,求的值.
A组
1.二次根式的最小值为( )
A.0 B.1
C.-1 D.不能确定
A
课时训练
2.下列式子中不是代数式的为( )
A.(x≥-2) B.5a+8=7
C.2 020 D.(a≠)
B
3.若x=+2,则|x-y|的值是( )
A.5 B.1 C.-1 D.2
B
4.若等式=x-8成立,则x的取值范围是
.
5.若式子3+x(x-1)0有意义,则x的取值范围是
.
6.已知y=-2,则xy的值为 .
x≥8
x≤2且x≠1
7.计算:
(1) ; (2);
(3)(x<3);
(4)()-1-(-1)0+.
解:(1)原式=6.
(2)原式=9.
(3)∵x<3,∴x-3<0.
∴原式==3-x.
(4)原式=2-1+3=4.
B组
8.如果有y=-2,求xy的值.
解:由题意,得x2-16≥0,且16-x2≥0.解得x=±4.
∵4-x≠0,∴x≠4.
∴x=-4.∴y=-2.
∴xy=(-4)-2=.
9.已知y=+8.求-x-3y的立方根.
解:∵y=+8,
∴x-3≥0,且3-x≥0,
解得x=3,
∴y=8,
∴-x-3y=-3-24=-27,
∴-x-3y的立方根为-3.
10.已知0<a<1,试化简:
.
解:+4=a2-2++4=a2+2+,
-4=a2+2+-4=a2-2+.
∴原式=
=.
∵0<a<1,∴a+>0,a-<0.
∴原式=a++a-=2a.
11.请认真阅读下面例题的解法,并回答拓展题.
例:已知y=+2 022,求的值.
解:由解得x=2 021,
∴y=2 022,
∴.
拓展题:已知=b+8.
(1)求a和b的值;
(2)求a2-b2的平方根.
解:(1)由解得a=17,
∴b=-8,
∴a=17,b=-8;
(2)a2-b2=172-82=225,
∵225的平方根是±15,
∴a2-b2的平方根是±15.
谢谢大家欣赏
