六年级下册数学人教版小升初专题复习-几何图形解决问题课件(共17张PPT)
文档属性
| 名称 | 六年级下册数学人教版小升初专题复习-几何图形解决问题课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 300.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 18:47:27 | ||
图片预览






文档简介
(共17张PPT)
几何图形解决问题
周长在实际生活中的运用
1.篱笆长度。
2.包装带的长度。
温馨提示
靠墙的一边一般不需要装篱笆。
根据实际情况而定。
面积在生活中的应用
1.先求面积,再求总产量:单位面积产量×面积=总产量
温馨提示
单位统一。
2.求单位面积产量:总产量÷面积=单位面积产量
温馨提示
联系生活实际,仔细审题。
表面积在生活中的应用
在实际生活中,表面积有时只需求若干个面的面积,例如游泳池四周和底
面贴瓷砖,制作烟囱的铁皮面积。
不规则容器的容积
这里的不规则容器一般上面部分不规则,下面一部分规则,可采用“倒置
法”。容器容积=水的体积+空气体积。
温馨提示
容积计算方法和体积计算方法一致,但容积<体积。因为容积的数据应
用容器内部测得的数据。
体积和容积在生活中的应用
在生活中往往要把一个物体锻造成另一个形状,在此过程中体积不变。
典例1
如图,苹苹的爸爸用全长20m的篱笆靠墙围了一块梯形菜地,梯形高6m。
这块菜地占地多少平方米?
菜地形状为梯形,求菜地面积就是求梯形面积。S=(a+b)h÷2。已
知篱笆长20m,包括了上下底之和与高,所以篱笆上下底之和为(20-6)
m。
(20-6)×6×=42(m2)
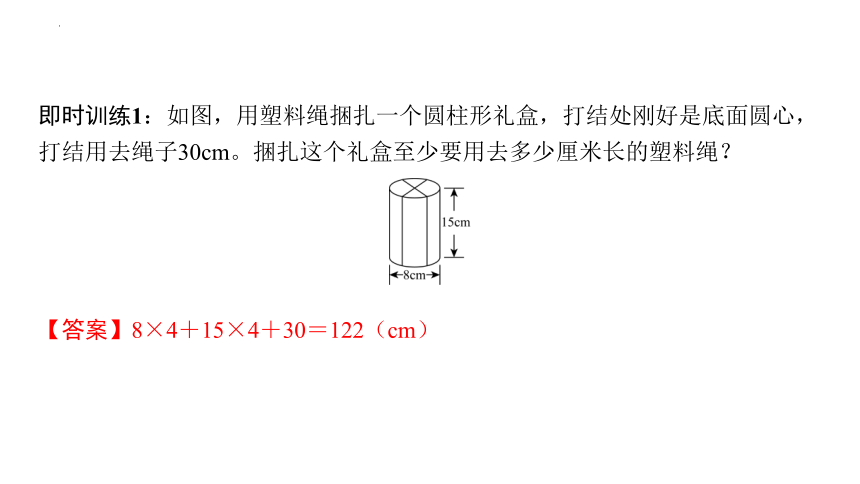
即时训练1:如图,用塑料绳捆扎一个圆柱形礼盒,打结处刚好是底面圆心,
打结用去绳子30cm。捆扎这个礼盒至少要用去多少厘米长的塑料绳?
【答案】8×4+15×4+30=122(cm)
典例2
在一个半径为5m的圆形花坛周围修一条宽2m的走道。走道的面积是多少平
方米?
本题中走道的面积就是环形的面积。环形面积=外圆面积-内圆面
积,即S环=πR2-πr2。
3.14×(5+2)2-3.14×52=75.36(m2)
即时训练2:用铁皮制作一个高是5dm,底面直径是4dm的圆柱形水桶(无
盖)。至少需要多少平方分米的铁皮?
【答案】3.14×4×5+3.14×(4÷2)2=75.36(dm2)
典例3
一个圆锥形碎石堆,底面直径为4m,高1.5m。把这堆碎石在12m宽的公路
上铺10cm厚的路面,能铺多少米?(得数保留一位小数)
此题把一个圆锥形的碎石堆改变成长方体形状,在此过程中碎石的体
积不变。要求碎石长方体的长,先求碎石体积,再求长方体的长(注意:
10cm=0.1m)。
碎石体积:3.14×(4÷2)2×1.5×=6.28(m3)
铺的长度:6.28÷(12×0.1)≈5.2(m)
即时训练3:将一个棱长为5dm的正方体铁块熔铸成底面积是60dm2的圆锥。
这个圆锥的高是多少分米?
【答案】5×5×5×3÷60=6.25(dm)
即时训练4:一个底面直径是20cm、高是25cm的无盖圆柱形铁皮容器中装有
水,水里浸没一个长9.42cm,宽8cm,高5cm的长方体铁块。从容器中取出铁
块后(假设水量未减少),容器中水面会下降多少厘米?
【答案】9.42×8×5÷[3.14×(20÷2)2]=1.2(cm)
一、填空。
1.用铁丝焊接一个长15厘米,宽10厘米,高12厘米的长方体框架,至少需要
铁丝( 148 )厘米。
2.一个圆柱形的粮囤,它的高是4m,侧面积为200.96m2,这个粮囤的底面积
是( 200.96 )m2。
3.一个圆柱形橡皮泥,底面积为12cm2,高为5cm,如果把它捏成一个等底的
圆锥,这个圆锥高是( 15 )cm;如果把它捏成一个等高圆锥,这个圆锥
底面积是( 36 )cm2。
4.把一个棱长为6cm的正方体削成一个最大的圆锥,圆锥的体积是
( 56.52 )cm3。
148
200.96
15
36
56.52
二、选择。
1.用3根长12dm的铁丝分别围一个正方形、长方形和圆(铁丝均无剩余),围
成的( C )的面积最大。
A.正方形 B.长方形 C.圆 D.确定
2.做一节底面直径为20cm,长为90cm的圆柱形烟囱,至少需要( A )cm2
的铁皮。
A.5652 B.5966 C.6280 D.28260
C
A
3.一个拧紧瓶盖的瓶子里装有一些水(如图),瓶中水的体积占瓶子容积的
( B )。
A. B.
C. D.
B
4.一个磁带盒的长是10cm,宽是6cm,高是1cm,将4个这样的磁带盒包成一
包,下面( A )最省包装纸。
A. B. C.
A
三、解决问题。
1.将1.44升水倒入如图中的两个长方体水槽中,使它们的水面高度相等。水面
高度是多少?(数据是水槽内尺寸)
【答案】1.44升=1440cm3
1440÷(12×10+8×5)=9(cm)
2.求如图这个零件的表面积和体积。(单位:cm)
【答案】表面积:5×5×6+3×3×4=186(cm2) 体积:53+33=152
(cm3)
3.一瓶装满的矿泉水,内直径是8cm。小明喝了一些,水的高度还有12cm,
把瓶盖扭紧后倒置放平,无水部分高度10cm。小明喝了多少毫升水?
【答案】3.14×(8÷2)2×10=502.4(毫升)
4.王老师用一张面积为828cm2的长方形纸板制作一个圆柱形教具,如图所
示。那么,制成的圆柱的体积是多少?
【答案】设圆柱底面直径为xcm。 2x×(x+3.14x)=828
8.28x2=828 x2=100 x=10 V:3.14×(10÷2)2×(10×2)=1570
(cm3)
几何图形解决问题
周长在实际生活中的运用
1.篱笆长度。
2.包装带的长度。
温馨提示
靠墙的一边一般不需要装篱笆。
根据实际情况而定。
面积在生活中的应用
1.先求面积,再求总产量:单位面积产量×面积=总产量
温馨提示
单位统一。
2.求单位面积产量:总产量÷面积=单位面积产量
温馨提示
联系生活实际,仔细审题。
表面积在生活中的应用
在实际生活中,表面积有时只需求若干个面的面积,例如游泳池四周和底
面贴瓷砖,制作烟囱的铁皮面积。
不规则容器的容积
这里的不规则容器一般上面部分不规则,下面一部分规则,可采用“倒置
法”。容器容积=水的体积+空气体积。
温馨提示
容积计算方法和体积计算方法一致,但容积<体积。因为容积的数据应
用容器内部测得的数据。
体积和容积在生活中的应用
在生活中往往要把一个物体锻造成另一个形状,在此过程中体积不变。
典例1
如图,苹苹的爸爸用全长20m的篱笆靠墙围了一块梯形菜地,梯形高6m。
这块菜地占地多少平方米?
菜地形状为梯形,求菜地面积就是求梯形面积。S=(a+b)h÷2。已
知篱笆长20m,包括了上下底之和与高,所以篱笆上下底之和为(20-6)
m。
(20-6)×6×=42(m2)
即时训练1:如图,用塑料绳捆扎一个圆柱形礼盒,打结处刚好是底面圆心,
打结用去绳子30cm。捆扎这个礼盒至少要用去多少厘米长的塑料绳?
【答案】8×4+15×4+30=122(cm)
典例2
在一个半径为5m的圆形花坛周围修一条宽2m的走道。走道的面积是多少平
方米?
本题中走道的面积就是环形的面积。环形面积=外圆面积-内圆面
积,即S环=πR2-πr2。
3.14×(5+2)2-3.14×52=75.36(m2)
即时训练2:用铁皮制作一个高是5dm,底面直径是4dm的圆柱形水桶(无
盖)。至少需要多少平方分米的铁皮?
【答案】3.14×4×5+3.14×(4÷2)2=75.36(dm2)
典例3
一个圆锥形碎石堆,底面直径为4m,高1.5m。把这堆碎石在12m宽的公路
上铺10cm厚的路面,能铺多少米?(得数保留一位小数)
此题把一个圆锥形的碎石堆改变成长方体形状,在此过程中碎石的体
积不变。要求碎石长方体的长,先求碎石体积,再求长方体的长(注意:
10cm=0.1m)。
碎石体积:3.14×(4÷2)2×1.5×=6.28(m3)
铺的长度:6.28÷(12×0.1)≈5.2(m)
即时训练3:将一个棱长为5dm的正方体铁块熔铸成底面积是60dm2的圆锥。
这个圆锥的高是多少分米?
【答案】5×5×5×3÷60=6.25(dm)
即时训练4:一个底面直径是20cm、高是25cm的无盖圆柱形铁皮容器中装有
水,水里浸没一个长9.42cm,宽8cm,高5cm的长方体铁块。从容器中取出铁
块后(假设水量未减少),容器中水面会下降多少厘米?
【答案】9.42×8×5÷[3.14×(20÷2)2]=1.2(cm)
一、填空。
1.用铁丝焊接一个长15厘米,宽10厘米,高12厘米的长方体框架,至少需要
铁丝( 148 )厘米。
2.一个圆柱形的粮囤,它的高是4m,侧面积为200.96m2,这个粮囤的底面积
是( 200.96 )m2。
3.一个圆柱形橡皮泥,底面积为12cm2,高为5cm,如果把它捏成一个等底的
圆锥,这个圆锥高是( 15 )cm;如果把它捏成一个等高圆锥,这个圆锥
底面积是( 36 )cm2。
4.把一个棱长为6cm的正方体削成一个最大的圆锥,圆锥的体积是
( 56.52 )cm3。
148
200.96
15
36
56.52
二、选择。
1.用3根长12dm的铁丝分别围一个正方形、长方形和圆(铁丝均无剩余),围
成的( C )的面积最大。
A.正方形 B.长方形 C.圆 D.确定
2.做一节底面直径为20cm,长为90cm的圆柱形烟囱,至少需要( A )cm2
的铁皮。
A.5652 B.5966 C.6280 D.28260
C
A
3.一个拧紧瓶盖的瓶子里装有一些水(如图),瓶中水的体积占瓶子容积的
( B )。
A. B.
C. D.
B
4.一个磁带盒的长是10cm,宽是6cm,高是1cm,将4个这样的磁带盒包成一
包,下面( A )最省包装纸。
A. B. C.
A
三、解决问题。
1.将1.44升水倒入如图中的两个长方体水槽中,使它们的水面高度相等。水面
高度是多少?(数据是水槽内尺寸)
【答案】1.44升=1440cm3
1440÷(12×10+8×5)=9(cm)
2.求如图这个零件的表面积和体积。(单位:cm)
【答案】表面积:5×5×6+3×3×4=186(cm2) 体积:53+33=152
(cm3)
3.一瓶装满的矿泉水,内直径是8cm。小明喝了一些,水的高度还有12cm,
把瓶盖扭紧后倒置放平,无水部分高度10cm。小明喝了多少毫升水?
【答案】3.14×(8÷2)2×10=502.4(毫升)
4.王老师用一张面积为828cm2的长方形纸板制作一个圆柱形教具,如图所
示。那么,制成的圆柱的体积是多少?
【答案】设圆柱底面直径为xcm。 2x×(x+3.14x)=828
8.28x2=828 x2=100 x=10 V:3.14×(10÷2)2×(10×2)=1570
(cm3)
同课章节目录
