四年级下册数学人教版《乘除法的意义和各部分间的关系》课件(共23张PPT)
文档属性
| 名称 | 四年级下册数学人教版《乘除法的意义和各部分间的关系》课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 711.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
乘、除法的意义和
各部分间的关系
人民教育出版社义务教育四年级下册
一、创设情境,引入新课
每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
二、探究规律,明确意义
(一)探究活动一:明确乘法的意义
3+3+3+3=12
3 × 4 =12
问题:你认为什么是乘法?
求几个相同加数的和的简便运算,叫做乘法。
因数×因数
相乘的两个数叫做因数。
乘得的数叫做积。
=积
乘号的由来
17世纪前,有人用字母M和D分别表示乘法和除法。
1631年,英国数学家奥特雷德发现乘法也是相加的意思,但是又和加法有所不同,怎么表示更合适呢?他想,能不能把“+”号旋转45度,斜过来用“×”表示乘法呢?乘号问世了。
实际上, “×”和“ · ”这两个乘号同时被使用着,一直沿袭到今天。
3×a可记作3·a,或3a
a×b可记作a·b ,或ab
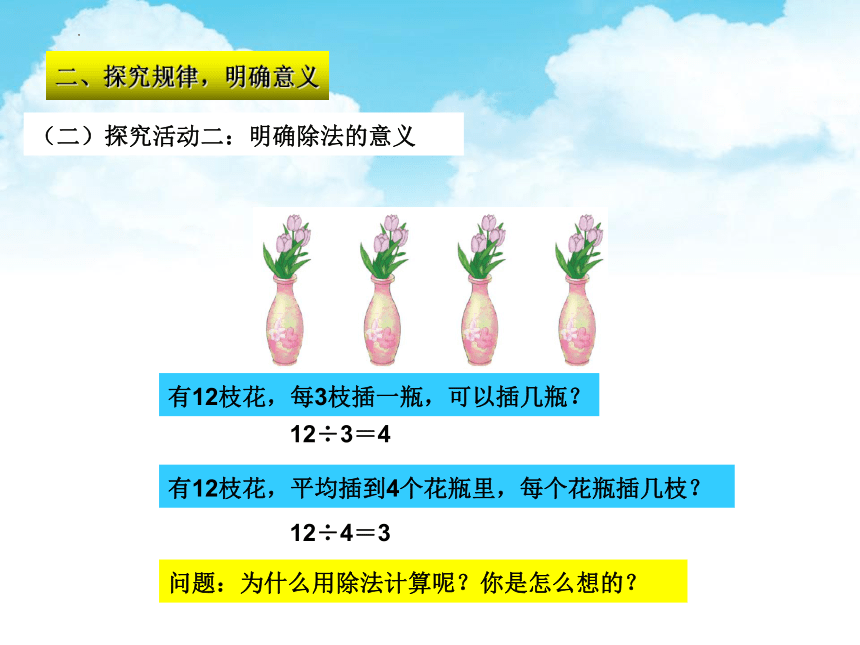
12÷3=4
问题:为什么用除法计算呢?你是怎么想的?
12÷4=3
(二)探究活动二:明确除法的意义
有12枝花,每3枝插一瓶,可以插几瓶?
有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
二、探究规律,明确意义
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
3×4=12
12÷3=4
12÷4=3
(二)探究活动二:明确除法的意义
二、探究规律,明确意义
问题:与第(1)相比,第(2)、(3)题分别是已知什么?
求什么?怎样算?
问题:用你自己的话说一说,你认为什么是除法?
已知两个因数的积与其中一个因数,求另一个因数的运算,
叫做除法。
(1)
3×4=12
(2)
12÷3=4
(3)
12÷4=3
(二)探究活动二:明确除法的意义
在除法中,已知的积叫做被除数,已知的因数叫做除数,所
求的因数叫做商。
1. 乘法各部分间的关系
积=因数×因数
问题:如果知道积与一个因数,能求出另一个因数吗?
另一个因数=积÷一个因数
(三)探究活动三:乘、除法各部分间的关系
二、探究规律,明确意义
商=被除数÷除数
问题:如果知道被除数和商,能求出除数吗?
除数=被除数÷商
问题:如果知道除数和商,能求出被除数吗?
2. 除法各部分间的关系
(三)探究活动三:乘、除法各部分间的关系
二、探究规律,明确意义
被除数=商×除数
问题:你认为乘法与除法间有什么关系?
除法是乘法的逆运算。
3. 乘法与除法间的关系
(三)探究活动三:乘、除法各部分间的关系
二、探究规律,明确意义
想一想:在有余数的除法里,被除数与商、除数和余数
之间有什么关系?
15÷7=2……1
被除数=商×除数+余数
4. 乘法与除法间的关系
(三)探究活动三:乘、除法各部分间的关系
二、探究规律,明确意义
三、总结感悟,看书质疑
问题:你是根据什么得出结果的?
1. 根据36×14=504,直接写出下面两道题的得数。
504÷14=
504÷36=
36
14
四、巩固提升,学以致用
17×42=714
208×67=13936
714÷17=42
714÷42=17
13936÷208=67
13936÷67=208
四、巩固提升,学以致用
2.根据乘、除法各部分间的关系,写出另外两个算式。
1125÷25=45
1008÷48=21
45×25=1125
21×48=1008
四、巩固提升,学以致用
2.根据乘、除法各部分间的关系,写出另外两个算式。
25×45=1125
48×21=1008
(1)蜗牛每小时可爬行5米,6小时可爬行多少米?
3、下面各题应该用什么方法计算?为什么?
(2)120枝铅笔,每12枝装一盒,可以装几盒?
(3)蜗牛6小时爬行30米,平均每小时爬行多少米?
(4)一头大象的体重是5600千克,正好是一头水 牛的8倍,这头牛重多少千克?
四、巩固提升,学以致用
四、巩固提升,学以致用
(1)蜗牛每小时可爬行5米,6小时可爬行多少米?
分析:每小时爬行的米数 × 爬行的时间 = 爬行的总米数
5
6
?
5×6=30(米)
(2)120枝铅笔,每12枝装一盒,可以装几盒?
分析:每盒的支数 × 盒数 = 总的铅笔数
120÷12=10(盒)
四、巩固提升,学以致用
12
?
120
四、巩固提升,学以致用
(3)蜗牛6小时爬行30米,平均每小时爬行多少米?
分析:每小时爬行的米数 × 爬行的时间 = 爬行的路程
30÷6=5(米)
?
6
30
(4)一头大象的体重是5600千克,正好是一头水牛的 8倍,这头牛重多少千克?
分析:水牛的体重 × 8 = 大象的体重
5600÷8=700(千克)
四、巩固提升,学以致用
?
5600
8
已知 + = , × = ,下面
哪些算式是正确的?正确的画“√”,错误的画“×”
1、 + = ( )
2、 - = ( )
3、 ÷ = ( )
4、 × = ( )
√
√
×
×
四、巩固提升,学以致用
乘、除法的意义和
各部分间的关系
人民教育出版社义务教育四年级下册
一、创设情境,引入新课
每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
二、探究规律,明确意义
(一)探究活动一:明确乘法的意义
3+3+3+3=12
3 × 4 =12
问题:你认为什么是乘法?
求几个相同加数的和的简便运算,叫做乘法。
因数×因数
相乘的两个数叫做因数。
乘得的数叫做积。
=积
乘号的由来
17世纪前,有人用字母M和D分别表示乘法和除法。
1631年,英国数学家奥特雷德发现乘法也是相加的意思,但是又和加法有所不同,怎么表示更合适呢?他想,能不能把“+”号旋转45度,斜过来用“×”表示乘法呢?乘号问世了。
实际上, “×”和“ · ”这两个乘号同时被使用着,一直沿袭到今天。
3×a可记作3·a,或3a
a×b可记作a·b ,或ab
12÷3=4
问题:为什么用除法计算呢?你是怎么想的?
12÷4=3
(二)探究活动二:明确除法的意义
有12枝花,每3枝插一瓶,可以插几瓶?
有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
二、探究规律,明确意义
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
3×4=12
12÷3=4
12÷4=3
(二)探究活动二:明确除法的意义
二、探究规律,明确意义
问题:与第(1)相比,第(2)、(3)题分别是已知什么?
求什么?怎样算?
问题:用你自己的话说一说,你认为什么是除法?
已知两个因数的积与其中一个因数,求另一个因数的运算,
叫做除法。
(1)
3×4=12
(2)
12÷3=4
(3)
12÷4=3
(二)探究活动二:明确除法的意义
在除法中,已知的积叫做被除数,已知的因数叫做除数,所
求的因数叫做商。
1. 乘法各部分间的关系
积=因数×因数
问题:如果知道积与一个因数,能求出另一个因数吗?
另一个因数=积÷一个因数
(三)探究活动三:乘、除法各部分间的关系
二、探究规律,明确意义
商=被除数÷除数
问题:如果知道被除数和商,能求出除数吗?
除数=被除数÷商
问题:如果知道除数和商,能求出被除数吗?
2. 除法各部分间的关系
(三)探究活动三:乘、除法各部分间的关系
二、探究规律,明确意义
被除数=商×除数
问题:你认为乘法与除法间有什么关系?
除法是乘法的逆运算。
3. 乘法与除法间的关系
(三)探究活动三:乘、除法各部分间的关系
二、探究规律,明确意义
想一想:在有余数的除法里,被除数与商、除数和余数
之间有什么关系?
15÷7=2……1
被除数=商×除数+余数
4. 乘法与除法间的关系
(三)探究活动三:乘、除法各部分间的关系
二、探究规律,明确意义
三、总结感悟,看书质疑
问题:你是根据什么得出结果的?
1. 根据36×14=504,直接写出下面两道题的得数。
504÷14=
504÷36=
36
14
四、巩固提升,学以致用
17×42=714
208×67=13936
714÷17=42
714÷42=17
13936÷208=67
13936÷67=208
四、巩固提升,学以致用
2.根据乘、除法各部分间的关系,写出另外两个算式。
1125÷25=45
1008÷48=21
45×25=1125
21×48=1008
四、巩固提升,学以致用
2.根据乘、除法各部分间的关系,写出另外两个算式。
25×45=1125
48×21=1008
(1)蜗牛每小时可爬行5米,6小时可爬行多少米?
3、下面各题应该用什么方法计算?为什么?
(2)120枝铅笔,每12枝装一盒,可以装几盒?
(3)蜗牛6小时爬行30米,平均每小时爬行多少米?
(4)一头大象的体重是5600千克,正好是一头水 牛的8倍,这头牛重多少千克?
四、巩固提升,学以致用
四、巩固提升,学以致用
(1)蜗牛每小时可爬行5米,6小时可爬行多少米?
分析:每小时爬行的米数 × 爬行的时间 = 爬行的总米数
5
6
?
5×6=30(米)
(2)120枝铅笔,每12枝装一盒,可以装几盒?
分析:每盒的支数 × 盒数 = 总的铅笔数
120÷12=10(盒)
四、巩固提升,学以致用
12
?
120
四、巩固提升,学以致用
(3)蜗牛6小时爬行30米,平均每小时爬行多少米?
分析:每小时爬行的米数 × 爬行的时间 = 爬行的路程
30÷6=5(米)
?
6
30
(4)一头大象的体重是5600千克,正好是一头水牛的 8倍,这头牛重多少千克?
分析:水牛的体重 × 8 = 大象的体重
5600÷8=700(千克)
四、巩固提升,学以致用
?
5600
8
已知 + = , × = ,下面
哪些算式是正确的?正确的画“√”,错误的画“×”
1、 + = ( )
2、 - = ( )
3、 ÷ = ( )
4、 × = ( )
√
√
×
×
四、巩固提升,学以致用
