人教版小学数学六年级下册《小升初专题复习-探索规律》课件(共23张PPT)
文档属性
| 名称 | 人教版小学数学六年级下册《小升初专题复习-探索规律》课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 619.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 18:49:59 | ||
图片预览








文档简介
(共23张PPT)
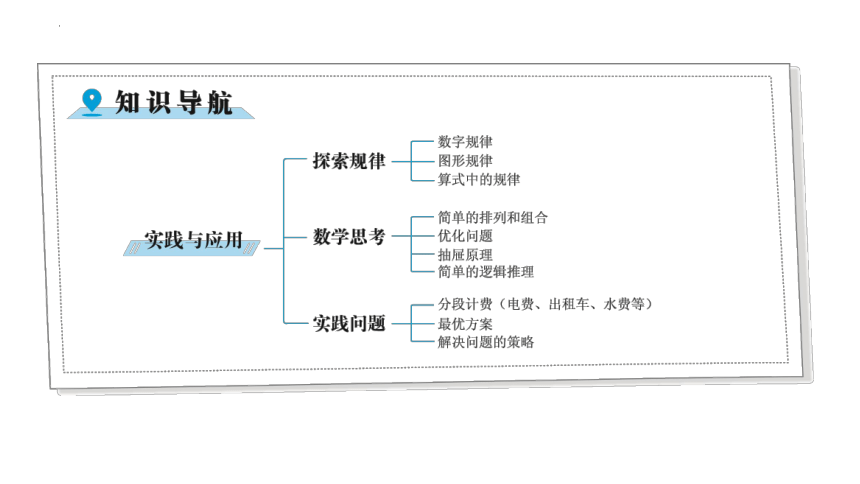
探索规律
数字中的规律
1.数列:按一定次序排列的一列数叫作数列。
温馨提示
探索数字规律一般先从数列中相邻两数之间的关系入手。
2.数列中的规律
(1)规律隐含在相邻两数的和或差中。
(2)规律隐含在相邻两数的倍数中。
(3)前后几项为一组,以组为单位隐含一定的规律。
(4)相隔的项之间存在着一定的规律。
(5)数列的各项分别是项数的平方数。
(6)数列中的下一项是前几项的和。
图形中的规律
1.图形规律是指根据一组相关图形总结出图形变化所反映的规律。
智慧锦囊
在探索数与形结合的规律时,一方面需要考虑图形的特点,另一方面需
要考虑数的排列规律,用数形结合、对应、转化等思想去解决问题。
2.解决图形规律问题的方法有两种:一种是数图形,将图形转化成数字规
律,再用数字规律解决问题;另一种是通过图形的直观性,从图形的变化中
直接寻找规律。
算式中的规律
1.利用计算器独立探索,发现规律。
2.利用规律来完成计算。
温馨提示
根据算式中提供的某些信息,通过观察、类比、推理、反思,从而归
纳、猜测、验证得出一般性的规律和结论。
典例1
按规律填空。
(1)1,1,2,3,5,8,( ),( )。
(2)3,5,9,17,33,65,( )。
此题主要考查探索数列中数字排列规律的能力。(1)观察发现:1+1
=2,1+2=3,2+3=5,3+5=8,得出从第三个数开始,每个数都是它前
面两个数的和,因此后两个空里的数分别是5+8和8+13。(2)通过列表寻
找规律,如下所示:
(1)13 21 (2)129
即时训练1:按规律填空。
(1)4,9,16,( 25 ),36,( 49 ),( 64 )。
(2),-,,-,( ),( - ),。
(3)1,5,14,30,55,( 91 )。
(4),,( ),,,( )。
25
49
64
-
91
即时训练2:在方格中填上合适的数。
1 2
5 3
4 5
29 6
7 8
71 9
10 11
131 12
71
10
11
131
12
典例2
如图,用火柴棒拼三角形。拼10个三角形需要多少根火柴棒?
此题主要考查探索图形规律的能力,观察如图可知,拼1个三角形需要
3根火柴棒,拼2个三角形需要5根火柴棒……可通过列表进行分析:
三角形个数 1 2 3 4 5 6
火柴棒根数 3 5 7 9 11 13
由上表可知,当拼n个三角形时,需要火柴棒的数量为(2n+1)根。
拼10个三角形需要21根火柴棒。
即时训练3:用小棒摆图形,如图:
摆n个八边形需要( 1+7n )根小棒;2017根小棒可摆( 288 )个
八边形。
1+7n
288
典例3
根据各式的规律填数。
1=12
1+3=22
1+3+5=32
1+3+5+7=42
(1)1+3+5+7+9+11+13=( )。
(2)从1开始,( )个连续奇数相加的和是202。
观察算式可知,从1开始的连续奇数的和等于奇数个数的平方,然后计
算即可得解。
(1)72 (2)20
即时训练4:观察下面的算式,找出规律后接着写两个算式。
111×999=110889
1111×9999=11108889
11111×99999=1111088889
111111×999999=111110888889
1111111×9999999=11111108888889
典例4
一列数1,1,2,3,5,8,13,21,34,55,…,从第三个数开始,每个
数都是前两个数之和。那么在前1000个数中,有( )个奇数。
仔细观察这列数,可以发现它是按“奇、奇、偶、奇、奇、偶……”
的顺序成周期性排列,在前1000个数中,如果每3个数分为一组,那么每一组
中有2个奇数。
667
即时训练5:一列数,前两个数都是1,从第三个数开始,每个数都是前两个
数的和,即1,1,2,3,5,8,13,…到第2000个数为止,共有( D )
个奇数。
A.668 B.1332 C.1333 D.1334
D
一、填空。
1.找规律,填一填。
(1),,,,( ),( )。
(2),,,,,,( 1 ),( ),3。
2.先观察下面各算式,找出规律,再根据规律填空。
①21×9=189 ②321×9=2889 ③4321×9=38889
④( 54321 )×9=488889
⑤( 654321 )×9=( 5888889 )
1
54321
654321
5888889
3.按下面的摆法,第25个三角形是( 黑 )色的;摆80个三角形,有
( 39 )个是白色的。
▲▲△△▲△▲▲△△▲△▲▲…
4.
…
如图,摆6个六边形要( 31 )根小棒,照这样摆下去,151根小棒可以摆
( 30 )个六边形。
5.一串数:1,3,6,10,15,21,28,…那么这串数的第100个数与第98个
数的差是( 199 )。
黑
39
31
30
199
2+4=2×3
2+4+6=3×4
2+4+6+8=4×5
2+4+6+8+10+…+50=( 25 )×( 26 )
25
26
6.观察下列算式,寻找规律填数。
二、选择。
1.由数字0,4,5可以组成( B )个不同的三位数。
A.3 B.4 C.5 D.6
2.如图是由涂色正方形与没有涂色正方形排列而成,按规律排列下去,当刚
好出现第7个涂色正方形时,则涂色正方形个数是没有涂色正方形个数的
( A )。
…
A. B. C. D.以上答案都不对
B
A
3.按如图方式摆放桌子和椅子。
…
当摆放8张桌子时,可以坐( C )人。
A.30 B.32 C.34 D.36
C
4.如图是一个装饰物品连续旋转闪烁所成的三个图形,照此规律闪烁,下一
个呈现出来的图形是( B )。
…
A. B. C. D.
B
5.观察下面各图,找出图中数与数之间的变化规律。“?”处应填( A )。
A.4 B.5 C.6 D.7
A
三、解决问题。
1.观察右面的图形和算式,看一看有什么规律并把算式补充完整。
1=12
1+2+1=22
1+2+3+2+1=( 3 )2
你能利用规律写一写下面的算式吗?
1+2+3+4+3+2+1=( 4 )2
1+2+3+4+5+4+3+2+1=( 5 )2
…
( 1+2+3+4+5+6+7+8+7+6+5+4+3+2+1 )=82
3
4
5
1+2+3+4+5+6+7+8+7+6+5+4+3+2+1
2.图①是棱长为a的小正方体,图②、图③由这样的小正方体摆放而成,按这
样的方式继续摆放,由上而下分别叫第1层,第2层,……,第n层,第n层的
小正方体的个数为S。
(1)按要求填表。
n 1 2 3 4 5 …
S 1 3 6 10 15 …
(2)当n=10时,S= 。
10
15
55
探索规律
数字中的规律
1.数列:按一定次序排列的一列数叫作数列。
温馨提示
探索数字规律一般先从数列中相邻两数之间的关系入手。
2.数列中的规律
(1)规律隐含在相邻两数的和或差中。
(2)规律隐含在相邻两数的倍数中。
(3)前后几项为一组,以组为单位隐含一定的规律。
(4)相隔的项之间存在着一定的规律。
(5)数列的各项分别是项数的平方数。
(6)数列中的下一项是前几项的和。
图形中的规律
1.图形规律是指根据一组相关图形总结出图形变化所反映的规律。
智慧锦囊
在探索数与形结合的规律时,一方面需要考虑图形的特点,另一方面需
要考虑数的排列规律,用数形结合、对应、转化等思想去解决问题。
2.解决图形规律问题的方法有两种:一种是数图形,将图形转化成数字规
律,再用数字规律解决问题;另一种是通过图形的直观性,从图形的变化中
直接寻找规律。
算式中的规律
1.利用计算器独立探索,发现规律。
2.利用规律来完成计算。
温馨提示
根据算式中提供的某些信息,通过观察、类比、推理、反思,从而归
纳、猜测、验证得出一般性的规律和结论。
典例1
按规律填空。
(1)1,1,2,3,5,8,( ),( )。
(2)3,5,9,17,33,65,( )。
此题主要考查探索数列中数字排列规律的能力。(1)观察发现:1+1
=2,1+2=3,2+3=5,3+5=8,得出从第三个数开始,每个数都是它前
面两个数的和,因此后两个空里的数分别是5+8和8+13。(2)通过列表寻
找规律,如下所示:
(1)13 21 (2)129
即时训练1:按规律填空。
(1)4,9,16,( 25 ),36,( 49 ),( 64 )。
(2),-,,-,( ),( - ),。
(3)1,5,14,30,55,( 91 )。
(4),,( ),,,( )。
25
49
64
-
91
即时训练2:在方格中填上合适的数。
1 2
5 3
4 5
29 6
7 8
71 9
10 11
131 12
71
10
11
131
12
典例2
如图,用火柴棒拼三角形。拼10个三角形需要多少根火柴棒?
此题主要考查探索图形规律的能力,观察如图可知,拼1个三角形需要
3根火柴棒,拼2个三角形需要5根火柴棒……可通过列表进行分析:
三角形个数 1 2 3 4 5 6
火柴棒根数 3 5 7 9 11 13
由上表可知,当拼n个三角形时,需要火柴棒的数量为(2n+1)根。
拼10个三角形需要21根火柴棒。
即时训练3:用小棒摆图形,如图:
摆n个八边形需要( 1+7n )根小棒;2017根小棒可摆( 288 )个
八边形。
1+7n
288
典例3
根据各式的规律填数。
1=12
1+3=22
1+3+5=32
1+3+5+7=42
(1)1+3+5+7+9+11+13=( )。
(2)从1开始,( )个连续奇数相加的和是202。
观察算式可知,从1开始的连续奇数的和等于奇数个数的平方,然后计
算即可得解。
(1)72 (2)20
即时训练4:观察下面的算式,找出规律后接着写两个算式。
111×999=110889
1111×9999=11108889
11111×99999=1111088889
111111×999999=111110888889
1111111×9999999=11111108888889
典例4
一列数1,1,2,3,5,8,13,21,34,55,…,从第三个数开始,每个
数都是前两个数之和。那么在前1000个数中,有( )个奇数。
仔细观察这列数,可以发现它是按“奇、奇、偶、奇、奇、偶……”
的顺序成周期性排列,在前1000个数中,如果每3个数分为一组,那么每一组
中有2个奇数。
667
即时训练5:一列数,前两个数都是1,从第三个数开始,每个数都是前两个
数的和,即1,1,2,3,5,8,13,…到第2000个数为止,共有( D )
个奇数。
A.668 B.1332 C.1333 D.1334
D
一、填空。
1.找规律,填一填。
(1),,,,( ),( )。
(2),,,,,,( 1 ),( ),3。
2.先观察下面各算式,找出规律,再根据规律填空。
①21×9=189 ②321×9=2889 ③4321×9=38889
④( 54321 )×9=488889
⑤( 654321 )×9=( 5888889 )
1
54321
654321
5888889
3.按下面的摆法,第25个三角形是( 黑 )色的;摆80个三角形,有
( 39 )个是白色的。
▲▲△△▲△▲▲△△▲△▲▲…
4.
…
如图,摆6个六边形要( 31 )根小棒,照这样摆下去,151根小棒可以摆
( 30 )个六边形。
5.一串数:1,3,6,10,15,21,28,…那么这串数的第100个数与第98个
数的差是( 199 )。
黑
39
31
30
199
2+4=2×3
2+4+6=3×4
2+4+6+8=4×5
2+4+6+8+10+…+50=( 25 )×( 26 )
25
26
6.观察下列算式,寻找规律填数。
二、选择。
1.由数字0,4,5可以组成( B )个不同的三位数。
A.3 B.4 C.5 D.6
2.如图是由涂色正方形与没有涂色正方形排列而成,按规律排列下去,当刚
好出现第7个涂色正方形时,则涂色正方形个数是没有涂色正方形个数的
( A )。
…
A. B. C. D.以上答案都不对
B
A
3.按如图方式摆放桌子和椅子。
…
当摆放8张桌子时,可以坐( C )人。
A.30 B.32 C.34 D.36
C
4.如图是一个装饰物品连续旋转闪烁所成的三个图形,照此规律闪烁,下一
个呈现出来的图形是( B )。
…
A. B. C. D.
B
5.观察下面各图,找出图中数与数之间的变化规律。“?”处应填( A )。
A.4 B.5 C.6 D.7
A
三、解决问题。
1.观察右面的图形和算式,看一看有什么规律并把算式补充完整。
1=12
1+2+1=22
1+2+3+2+1=( 3 )2
你能利用规律写一写下面的算式吗?
1+2+3+4+3+2+1=( 4 )2
1+2+3+4+5+4+3+2+1=( 5 )2
…
( 1+2+3+4+5+6+7+8+7+6+5+4+3+2+1 )=82
3
4
5
1+2+3+4+5+6+7+8+7+6+5+4+3+2+1
2.图①是棱长为a的小正方体,图②、图③由这样的小正方体摆放而成,按这
样的方式继续摆放,由上而下分别叫第1层,第2层,……,第n层,第n层的
小正方体的个数为S。
(1)按要求填表。
n 1 2 3 4 5 …
S 1 3 6 10 15 …
(2)当n=10时,S= 。
10
15
55
同课章节目录
