六年级下册数学人教版小升初专题复习-数学思考(课件)(共23张PPT)
文档属性
| 名称 | 六年级下册数学人教版小升初专题复习-数学思考(课件)(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 309.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 18:49:54 | ||
图片预览








文档简介
(共23张PPT)
数学思考
简单的排列和组合
1.排列、组合:排列是把给定个数的元素按一定的顺序排成一列;组合是把
给定个数的元素按任意的顺序并成一组。
温馨提示
1.解决有关排列组合问题的关键是不重复,不遗漏地找出可能出现的所
有情况。
2.
2.解决排列、组合问题的基本原理:分类计数原理(也称加法原理)与分步
计数原理(也称乘法原理)。
(1)加法原理
完成某一件任务共有n类办法,在第一类办法中有m1种不同的方法,在第二类
办法中有m2种不同的方法……在第n类办法中有mn种不同的方法,那么完成这
件事有N=m1+m2+…+mn种不同的方法。
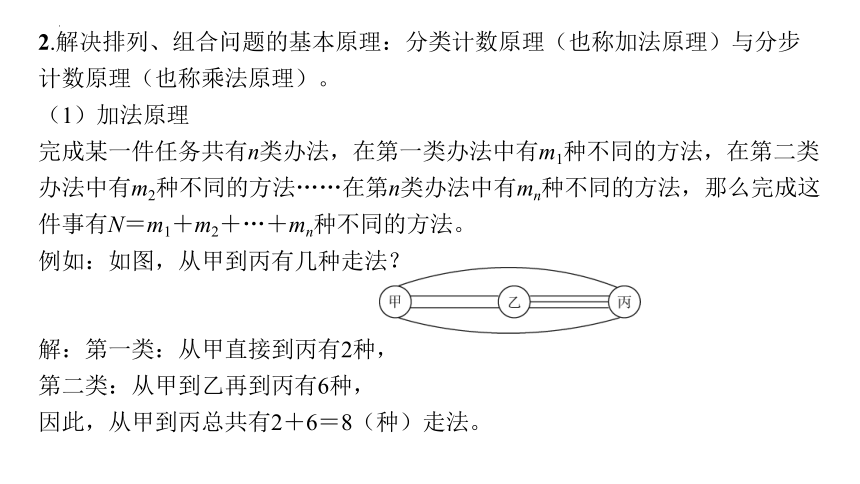
例如:如图,从甲到丙有几种走法?
解:第一类:从甲直接到丙有2种,
第二类:从甲到乙再到丙有6种,
因此,从甲到丙总共有2+6=8(种)走法。
(2)乘法原理
完成某一件任务有n个步骤,完成第一步有m1种不同的方法,完成第二步有m2
种不同的方法……完成第n步有mn种不同的方法,那么完成这件事有N=
m1×m2×…×mn种不同的方法。
优化问题
1.常见的优化问题
(1)找次品问题:在一些外观看似相同的物品中,有一个质量不同(轻
一点或重一点)的物品,需要我们想办法把它找出来。像这类问题就是
找次品问题。
(2)统筹时间问题:统筹时间问题就是研究如何合理安排时间,合理利用等
待时间,使得完成工作所用时间最少的问题。
温馨提示
天平称次品,用“三分法”称的次数最少。“三分法”是把要称的物品
尽可能平均分成三份。
要辨别的物品数量 保证能找出次品至少需要的次数
2~3 1
4~9 2
10~27 3
28~81 4
82~243 5
… …
注:只含1个次品,已知次品比正品轻
2.解决优化问题的方法:画图法、列表法、推理法。
抽屉原理
1.抽屉原理(一):把多于n个的物体放进n个抽屉里,则一定有一个抽屉里
至少放进了2个物体。(n是非0自然数)
计算方法:物体数÷抽屉数=商……余数 商+1=至少数
2.抽屉原理(二):把多于mn个的物体放进n个抽屉里,则一定有一个抽屉里
至少放进了(m+1)个物体。(m是正整数,n是非0自然数)
计算方法:物体数÷抽屉数=商……余数 商+1=至少数
温馨提示
解决有关抽屉原理的问题时,要理解“至少”的含义。
简单的逻辑推理
1.逻辑推理:根据已有的事实,经过分析、推理,就能找到答案。这种解决
问题的方法,就是逻辑推理。
2.简单的逻辑推理的方法:代换法、列表法、排除法、假设法、图解法。
数字编码
1.邮政编码:邮政编码由6位数字组成,前两位表示省(自治区、直辖市),
第三位表示邮区,第四位表示县(市),最后两位表示投递局(所)。
2.身份证编码:身份证号码由18位数字组成,第1,2位为各省级政府的代
码;第3,4位为地、市级政府的代码;第5,6位为县、区级政府的代码;第
7~14位为出生年月日;第15~17位为顺序号及性别区分,单数为男性分配
码,双数为女性分配码;第18位为校验码。
温馨提示
一个数字编码只能表达一个固定的信息,也就是说数字编码表达的信息
是唯一的。
典例1
如图,从A市到B市有2条不同的路,从B市到C市有5条不同的路。若从A市
经过B市到C市,则有多少条不同的路可以走?
从A市到B市有2条路,从B市到C市有5条路,由A市到B市的每一条路
都可以和B市到C市的5条路组合,因此就有2个5种不同的走法。
2×5=10(条) 答:有10条不同的路可以走。
即时训练1:有五个城市,每两个城市之间都有直达的航线。这五个城市之间
一共有( 10 )条不同的航线。
即时训练2:有红、黄、蓝三种不同颜色的信号灯,每次最多亮两种灯表示一
种信号,则这三种灯最多可表示( 6 )种信号。
10
6
典例2
8个质地、大小相同的球,其中有一个球较轻,用天平称,至少称( )
次可以找到较轻的球。
天平称次品,用“三分法”称的次数最少。如图所示:
2
即时训练3:有10瓶消炎药,其中9瓶质量相同,另有1瓶吃了3片。用天平
称,至少称几次就一定能找出吃了3片的那瓶?
【答案】3次
典例3
某校六年级有320人,他们的年龄分别为12岁、13岁,在这些同学中,至少
有多少名同学是同年同月出生的?
年龄最大的13岁,最小的12岁,即这些学生都是在两年内出生的,每
年有12个月,所以共有12×2=24种情况,看作24个抽屉。
年龄最大的13岁,最小的12岁,有两种年龄。
12×2=24(个)
320÷24=13(名)……8(名)
13+1=14(名)
答:至少有14名同学是同年同月出生的。
即时训练4:木箱里装有红球3个,黄球5个,蓝球7个,为保证取出的球中有
两个球的颜色不相同,则最少要取出多少个球?
【答案】8个
典例4
小东和甲、乙、丙、丁四个人进行象棋比赛。每两人要赛一场,到现在为
止,小东已经赛了4场,甲赛了3场,乙赛了2场,丁赛了1场,丙赛了
( )场。
可运用图解法进行推理。如图所示:
2
即时训练5:六年级有三个班,每班有2个班长。每次开班会时,每班只要一
个班长参加。会议记录表只写了他们的名字A,B,C,D,E,F,搞不清谁
与谁是同一个班的。本学期召开了两次班长会议,第一次到会的是A,B,
C;第二次到会的是B,D,C。根据这些信息,填“一定”“可能”或“不
可能”。
(1)A( 不可能 )和C同班。
(2)A( 一定 )和D同班。
不可能
一定
即时训练6:下面是小明的爷爷、奶奶、爸爸和妈妈四个人的身份证号码,你
知道各是谁的吗?填一填。
(1)370103198512210412是( 爸爸 )的身份证号码。
(2)370103196006070050是( 爷爷 )的身份证号码。
(3)370103198709180161是( 妈妈 )的身份证号码。
(4)370103196101010040是( 奶奶 )的身份证号码。
爸爸
爷爷
妈妈
奶奶
一、填空。
1.3件上衣和4条裤子,一件上衣与一条裤子搭配穿,有( 12 )种不同的
穿法。
2.光明小学有学生235人,至少有( 20 )人在同一个月出生,至少有
( 59 )人在同一季度出生。
3.一把钥匙只能开一把锁,现有6把钥匙6把锁,但不知道哪把钥匙开哪把
锁,要试( 15 )次才能保证配对成功。
4.一个班有50人,暑假期间有一个紧急演出,老师需尽快电话通知每一个同
学,如果每分钟通知1人至少要( 6 )分钟,才能通知到每一个人。
12
20
59
15
6
5.莎莎在一个早晨要完成的事情和所需要的时间如下:起床、穿衣服需要4分
钟;刷牙、洗脸、整理房间需要8分钟;煮鸡蛋需要10分钟;吃早饭需要6分
钟。经过合理安排,她最少需要( 20 )分钟就可以吃完早饭去上学。
6.小明、小刚、小强三名学生赛跑,比赛后有人问他们的名次。小明说:
“我不是第一名。”小刚说:“我不是第一名,也不是最后一名。”小强没
说话,那么,请你判断:第一名是( 小强 ),第二名是( 小刚 ),
第三名是( 小明 )。
7.在1+3+5+7+9+11+13+…中,从数“1”到数“23”的和是
( 144 )。
8.同学聚会,甲班来了9人,每两人握一次手,他们共握了( 36 )次手;
乙班来了8人,每人和甲班每位同学握一次手,共握了( 72 )次手。
20
小强
小刚
小明
144
36
72
二、选择。
1.有15盒饼干,其中的14盒质量相同,另有1盒少了几块,如果用天平称,至
少称( B )次。
A.2 B.3 C.4 D.5
2.用一只平底锅烙饼,每次最多只能烙2张。如果烙1张饼需要2分钟(正、反
面各需1分钟),那烙3张饼至少需要( A )分钟。
A.3 B.6 C.9
B
A
3.观察下面的算式:
5×9=45
55×99=5445
555×999=554445
5555×9999=55544445
则×=( C )。
A. 5 B. 5 C. 5
C
三、解决问题。
一个口袋里装有红球、白球和黄球各5个,这15个球除颜色不同其他都一样。
(1)至少要从口袋里摸出几个球才能保证其中有两个球的颜色相同?
【答案】3+1=4(个)
(2)至少要从口袋里摸出几个球才能保证其中有两个球的颜色不相同?
【答案】5+1=6(个)
数学思考
简单的排列和组合
1.排列、组合:排列是把给定个数的元素按一定的顺序排成一列;组合是把
给定个数的元素按任意的顺序并成一组。
温馨提示
1.解决有关排列组合问题的关键是不重复,不遗漏地找出可能出现的所
有情况。
2.
2.解决排列、组合问题的基本原理:分类计数原理(也称加法原理)与分步
计数原理(也称乘法原理)。
(1)加法原理
完成某一件任务共有n类办法,在第一类办法中有m1种不同的方法,在第二类
办法中有m2种不同的方法……在第n类办法中有mn种不同的方法,那么完成这
件事有N=m1+m2+…+mn种不同的方法。
例如:如图,从甲到丙有几种走法?
解:第一类:从甲直接到丙有2种,
第二类:从甲到乙再到丙有6种,
因此,从甲到丙总共有2+6=8(种)走法。
(2)乘法原理
完成某一件任务有n个步骤,完成第一步有m1种不同的方法,完成第二步有m2
种不同的方法……完成第n步有mn种不同的方法,那么完成这件事有N=
m1×m2×…×mn种不同的方法。
优化问题
1.常见的优化问题
(1)找次品问题:在一些外观看似相同的物品中,有一个质量不同(轻
一点或重一点)的物品,需要我们想办法把它找出来。像这类问题就是
找次品问题。
(2)统筹时间问题:统筹时间问题就是研究如何合理安排时间,合理利用等
待时间,使得完成工作所用时间最少的问题。
温馨提示
天平称次品,用“三分法”称的次数最少。“三分法”是把要称的物品
尽可能平均分成三份。
要辨别的物品数量 保证能找出次品至少需要的次数
2~3 1
4~9 2
10~27 3
28~81 4
82~243 5
… …
注:只含1个次品,已知次品比正品轻
2.解决优化问题的方法:画图法、列表法、推理法。
抽屉原理
1.抽屉原理(一):把多于n个的物体放进n个抽屉里,则一定有一个抽屉里
至少放进了2个物体。(n是非0自然数)
计算方法:物体数÷抽屉数=商……余数 商+1=至少数
2.抽屉原理(二):把多于mn个的物体放进n个抽屉里,则一定有一个抽屉里
至少放进了(m+1)个物体。(m是正整数,n是非0自然数)
计算方法:物体数÷抽屉数=商……余数 商+1=至少数
温馨提示
解决有关抽屉原理的问题时,要理解“至少”的含义。
简单的逻辑推理
1.逻辑推理:根据已有的事实,经过分析、推理,就能找到答案。这种解决
问题的方法,就是逻辑推理。
2.简单的逻辑推理的方法:代换法、列表法、排除法、假设法、图解法。
数字编码
1.邮政编码:邮政编码由6位数字组成,前两位表示省(自治区、直辖市),
第三位表示邮区,第四位表示县(市),最后两位表示投递局(所)。
2.身份证编码:身份证号码由18位数字组成,第1,2位为各省级政府的代
码;第3,4位为地、市级政府的代码;第5,6位为县、区级政府的代码;第
7~14位为出生年月日;第15~17位为顺序号及性别区分,单数为男性分配
码,双数为女性分配码;第18位为校验码。
温馨提示
一个数字编码只能表达一个固定的信息,也就是说数字编码表达的信息
是唯一的。
典例1
如图,从A市到B市有2条不同的路,从B市到C市有5条不同的路。若从A市
经过B市到C市,则有多少条不同的路可以走?
从A市到B市有2条路,从B市到C市有5条路,由A市到B市的每一条路
都可以和B市到C市的5条路组合,因此就有2个5种不同的走法。
2×5=10(条) 答:有10条不同的路可以走。
即时训练1:有五个城市,每两个城市之间都有直达的航线。这五个城市之间
一共有( 10 )条不同的航线。
即时训练2:有红、黄、蓝三种不同颜色的信号灯,每次最多亮两种灯表示一
种信号,则这三种灯最多可表示( 6 )种信号。
10
6
典例2
8个质地、大小相同的球,其中有一个球较轻,用天平称,至少称( )
次可以找到较轻的球。
天平称次品,用“三分法”称的次数最少。如图所示:
2
即时训练3:有10瓶消炎药,其中9瓶质量相同,另有1瓶吃了3片。用天平
称,至少称几次就一定能找出吃了3片的那瓶?
【答案】3次
典例3
某校六年级有320人,他们的年龄分别为12岁、13岁,在这些同学中,至少
有多少名同学是同年同月出生的?
年龄最大的13岁,最小的12岁,即这些学生都是在两年内出生的,每
年有12个月,所以共有12×2=24种情况,看作24个抽屉。
年龄最大的13岁,最小的12岁,有两种年龄。
12×2=24(个)
320÷24=13(名)……8(名)
13+1=14(名)
答:至少有14名同学是同年同月出生的。
即时训练4:木箱里装有红球3个,黄球5个,蓝球7个,为保证取出的球中有
两个球的颜色不相同,则最少要取出多少个球?
【答案】8个
典例4
小东和甲、乙、丙、丁四个人进行象棋比赛。每两人要赛一场,到现在为
止,小东已经赛了4场,甲赛了3场,乙赛了2场,丁赛了1场,丙赛了
( )场。
可运用图解法进行推理。如图所示:
2
即时训练5:六年级有三个班,每班有2个班长。每次开班会时,每班只要一
个班长参加。会议记录表只写了他们的名字A,B,C,D,E,F,搞不清谁
与谁是同一个班的。本学期召开了两次班长会议,第一次到会的是A,B,
C;第二次到会的是B,D,C。根据这些信息,填“一定”“可能”或“不
可能”。
(1)A( 不可能 )和C同班。
(2)A( 一定 )和D同班。
不可能
一定
即时训练6:下面是小明的爷爷、奶奶、爸爸和妈妈四个人的身份证号码,你
知道各是谁的吗?填一填。
(1)370103198512210412是( 爸爸 )的身份证号码。
(2)370103196006070050是( 爷爷 )的身份证号码。
(3)370103198709180161是( 妈妈 )的身份证号码。
(4)370103196101010040是( 奶奶 )的身份证号码。
爸爸
爷爷
妈妈
奶奶
一、填空。
1.3件上衣和4条裤子,一件上衣与一条裤子搭配穿,有( 12 )种不同的
穿法。
2.光明小学有学生235人,至少有( 20 )人在同一个月出生,至少有
( 59 )人在同一季度出生。
3.一把钥匙只能开一把锁,现有6把钥匙6把锁,但不知道哪把钥匙开哪把
锁,要试( 15 )次才能保证配对成功。
4.一个班有50人,暑假期间有一个紧急演出,老师需尽快电话通知每一个同
学,如果每分钟通知1人至少要( 6 )分钟,才能通知到每一个人。
12
20
59
15
6
5.莎莎在一个早晨要完成的事情和所需要的时间如下:起床、穿衣服需要4分
钟;刷牙、洗脸、整理房间需要8分钟;煮鸡蛋需要10分钟;吃早饭需要6分
钟。经过合理安排,她最少需要( 20 )分钟就可以吃完早饭去上学。
6.小明、小刚、小强三名学生赛跑,比赛后有人问他们的名次。小明说:
“我不是第一名。”小刚说:“我不是第一名,也不是最后一名。”小强没
说话,那么,请你判断:第一名是( 小强 ),第二名是( 小刚 ),
第三名是( 小明 )。
7.在1+3+5+7+9+11+13+…中,从数“1”到数“23”的和是
( 144 )。
8.同学聚会,甲班来了9人,每两人握一次手,他们共握了( 36 )次手;
乙班来了8人,每人和甲班每位同学握一次手,共握了( 72 )次手。
20
小强
小刚
小明
144
36
72
二、选择。
1.有15盒饼干,其中的14盒质量相同,另有1盒少了几块,如果用天平称,至
少称( B )次。
A.2 B.3 C.4 D.5
2.用一只平底锅烙饼,每次最多只能烙2张。如果烙1张饼需要2分钟(正、反
面各需1分钟),那烙3张饼至少需要( A )分钟。
A.3 B.6 C.9
B
A
3.观察下面的算式:
5×9=45
55×99=5445
555×999=554445
5555×9999=55544445
则×=( C )。
A. 5 B. 5 C. 5
C
三、解决问题。
一个口袋里装有红球、白球和黄球各5个,这15个球除颜色不同其他都一样。
(1)至少要从口袋里摸出几个球才能保证其中有两个球的颜色相同?
【答案】3+1=4(个)
(2)至少要从口袋里摸出几个球才能保证其中有两个球的颜色不相同?
【答案】5+1=6(个)
同课章节目录
