人教版五年级下册数学3的倍数的特征课件(共26张PPT)
文档属性
| 名称 | 人教版五年级下册数学3的倍数的特征课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 528.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 18:54:14 | ||
图片预览






文档简介
(共26张PPT)
3的倍数的特征
输入标题
学习目标
培养观察、比较和分析、概括等思维能力,积累数学活动经验,进一步发展数感。
掌握3的倍数的特征,能判断或写出3的倍数,并能说明判断理由。
主动参与探究、发现规律的活动,获得探索数学结论的成功体验,体会数学的奇妙,增强学习数学的积极情感。
个位是0、2、4、6、8
5的倍数的特征
个位是0、5
2和5的倍数的特征
个位是0
请你说出2、5倍数的特征
2的倍数的特征
我们知道了2和5的倍数的特征,猜一猜3的倍数有什么特征?
我猜个位上是3,6 或 9 的数是 3 的倍数。
不一定,13 就不是 3 的倍数。
3×1=3
3×2=6
3×3=9
3×4=12
3×5=15
3×6=18
3×7=21
3×8=24
3×9=27
……
个位上的数有没有规律?
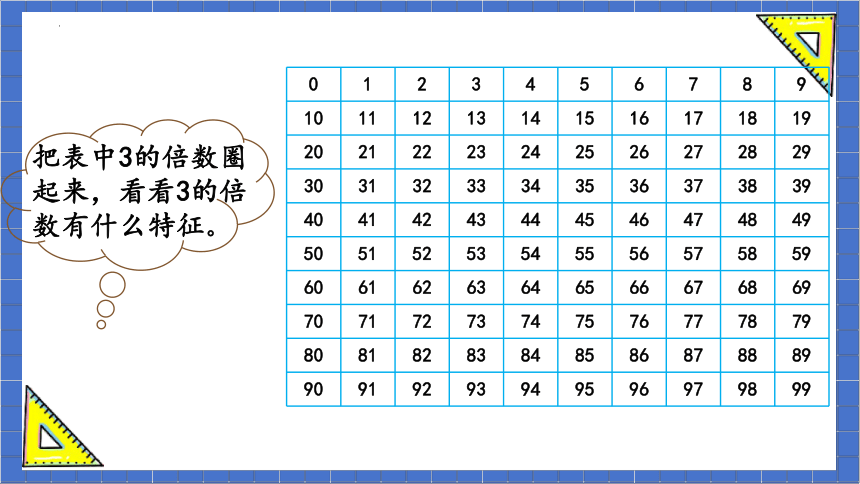
把表中3的倍数圈起来,看看3的倍数有什么特征。
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
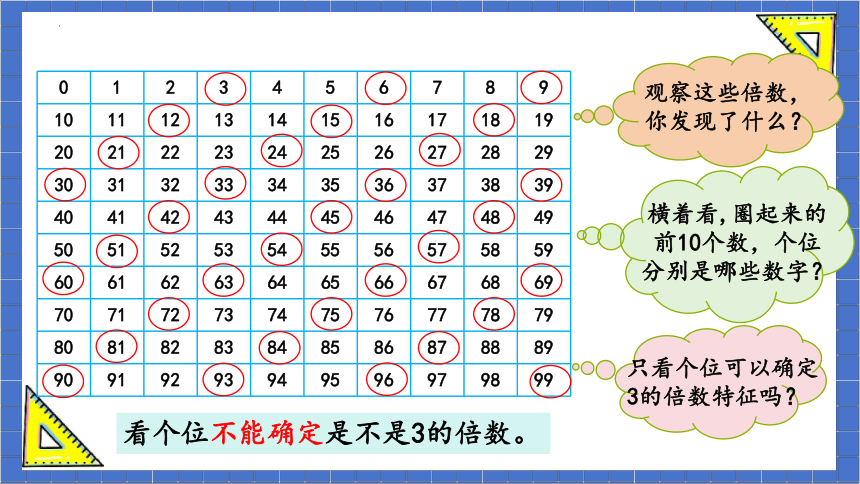
观察这些倍数,你发现了什么?
只看个位可以确定3的倍数特征吗?
横着看,圈起来的前10个数,个位分别是哪些数字?
看个位不能确定是不是3的倍数。
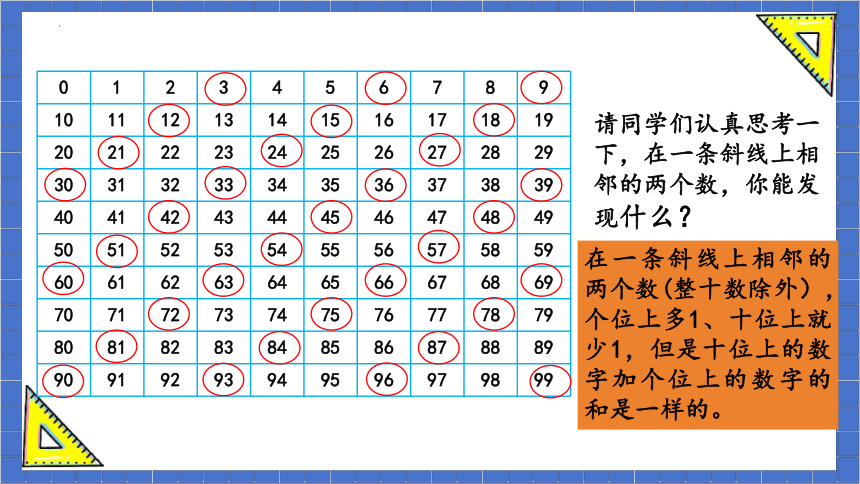
请同学们认真思考一下,在一条斜线上相邻的两个数,你能发现什么?
在一条斜线上相邻的两个数(整十数除外),个位上多1、十位上就少1,但是十位上的数字加个位上的数字的和是一样的。
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
3的倍数 各个数位上的数字和 发现
……
试着算一算这些数各个数位上的数字之和有什么规律。
12
15
18
21
24
1+2=3
1+5=6
1+8=9
2+1=3
2+4=6
3的倍数的各个数位上的数字之和是3的倍数。
斜着看,你发现了什么?
斜着看,3的倍数各位上的数的和都是3的倍数。
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。
你发现的规律对三位数、四位数成立吗?找几个数来检验一下。
3×274=822,822是3的倍数,8+2+2=12
2016 年开了奥运会,2 + 0 + 1 + 6 = 9,是 3 的倍数,2016 = 3×672,确实是 3 的倍数,太神奇啦!
3×65=195,195是3的倍数,1+9+5=15
这几个数各个数位上的数字之和是3的倍数。
1.判断一个数是不是3的倍数,不能只看这个数个位上的数,而要看它各数位上的数的和。
2.在判断一个大数是不是3的倍数时,如果这个大数各数位上的数的和仍然很大,那么可以把加得的和的各数位上的数再相加,如果得到的结果是3的倍数,那么这个大数就是3的倍数,否则就不是。
1.一个数同时是2、3的倍数,这个数有什么特征
这个数的特征是:偶数,且各数位上的数的和是3的倍数。
3.一个数同时是2、3、5的倍数,这个数有什么特征
这个数的特征是:个位上是0或5,且各数位上的数的和是3的倍数。
2.一个数同时是3、5的倍数,这个数有什么特征
这个数的特征是:个位上是0,且各数位上的数的和是3的倍数。
课堂练习
2+4=6,6是3的倍数,所以24是3的倍数。增加的卡片可以是0。2+4+0=6,240是3的倍数。
下面用数字卡片摆出的数中,哪些是3的倍数?在每个数后面增加一张卡片,使这个三位数成为3的倍数。
2
4
5
8
4
6
9
6
还可以是3,6,9。2+4+3=9,243是3的倍数;2+4+6=12,246是3的倍数;2+4+9=15,249是3的倍数。
后面可以加0 3 6 9这些数字的卡片。
2
4
课堂练习
9+6=15,15是3的倍数,所以96是3的倍数。增加的卡片可以是0。9+6+0=15,960是3的倍数。
还可以是3,6,9。9+6+3=18,963是3的倍数;9+6+6=21,9666是3的倍数;9+6+9=24,969是3的倍数。
后面可以加0 3 6 9这些数字的卡片。
9
6
圈出3的倍数。
92 75 36 206 65 3051 779 9999
111 49 165 5988 655 131 2222 7203
判断一个数是不是3的倍数,不能只看这个数个位上的数,而要看它各数位上的数的和。如果得到的结果是3的倍数,那么这个大数就是3的倍数,否则就不是。
选出两个数字组成一个两位数,分别满足下面的条件。
0
3
4
5
(1)是3的倍数:
(2)同时是2和3的倍数:
(3)同时是3和5的倍数:
(4)同时是2、3和5的倍数:
30、45、54
30、54
45、30
30
你能说出3个是3的倍数的偶数吗?
你能说出3个是5的倍数的奇数吗?
3的倍数是偶数的有6,12,18。
5的倍数是奇数的有15,25,35。
答案不唯一,合理即可。
□7 4□2 □44 65□ 12□1
在□里填一个数字,使每个数都是3的倍数。
2
5
8
0
3
6
9
1
4
7
1
4
7
2
5
8
各有几种填法?
至少再来 2 个人才能正好分完。
3 个人一组,总人数应是3的倍数,
22 最少加 2 才是 3 的倍数。
现在有22名学生分组玩游戏,至少再来几名学生就可以正好3人一组
下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)个位是3、6、9的数一定是3的倍数。( )
×
(2)用2、4、9组成的三位数都是3的倍数 。 ( )
√
(3)一个三位数各个数位上的数字都相同,这个数一定是3的倍数 。 ( )
√
(4)连续三个自然数的和一定是3的倍数。 ( )
√
个位上必须是0,2,4,6,8。
既是2的倍数,又是3的倍数的最小三位数是
______,最大三位数是______。
各位上的数字之和必须是3的倍数。
102
996
2、3的倍数
个位上是0,2,4,6,8,且各个数位上的数字之和是3的倍数。
个位上必须是0,5。
既是5的倍数,又是3的倍数的最小两位数是
______,最大两位数是______。
各位上的数字之和必须是3的倍数。
30
75
3、5的倍数
个位上是0,5,且各个数位上的数字之和是3的倍数。
既是2和5的倍数,又是3的倍数的最小两位数
是______。
30
个位上必须是0。
各位上的数字之和必须是3的倍数。
2、3、5的倍数
个位上是0,且各个数位上的数字之和是3的倍数。
冬冬到文具店买日记本,日记本的单价已经看不清楚了,他买了3本同样的日记本,售货员阿姨说应付34元,冬冬认为不对。你能解释这是为什么吗?
因为冬冬买了3本同样的日记本,不管日记本的单价是多少,应付的钱都应该是3的倍数,而34不是3的倍数,所以冬冬认为不对。
课堂小结
同学们,今天的数学课你们有哪些收获呢?
3的倍数的特征
输入标题
学习目标
培养观察、比较和分析、概括等思维能力,积累数学活动经验,进一步发展数感。
掌握3的倍数的特征,能判断或写出3的倍数,并能说明判断理由。
主动参与探究、发现规律的活动,获得探索数学结论的成功体验,体会数学的奇妙,增强学习数学的积极情感。
个位是0、2、4、6、8
5的倍数的特征
个位是0、5
2和5的倍数的特征
个位是0
请你说出2、5倍数的特征
2的倍数的特征
我们知道了2和5的倍数的特征,猜一猜3的倍数有什么特征?
我猜个位上是3,6 或 9 的数是 3 的倍数。
不一定,13 就不是 3 的倍数。
3×1=3
3×2=6
3×3=9
3×4=12
3×5=15
3×6=18
3×7=21
3×8=24
3×9=27
……
个位上的数有没有规律?
把表中3的倍数圈起来,看看3的倍数有什么特征。
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
观察这些倍数,你发现了什么?
只看个位可以确定3的倍数特征吗?
横着看,圈起来的前10个数,个位分别是哪些数字?
看个位不能确定是不是3的倍数。
请同学们认真思考一下,在一条斜线上相邻的两个数,你能发现什么?
在一条斜线上相邻的两个数(整十数除外),个位上多1、十位上就少1,但是十位上的数字加个位上的数字的和是一样的。
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
3的倍数 各个数位上的数字和 发现
……
试着算一算这些数各个数位上的数字之和有什么规律。
12
15
18
21
24
1+2=3
1+5=6
1+8=9
2+1=3
2+4=6
3的倍数的各个数位上的数字之和是3的倍数。
斜着看,你发现了什么?
斜着看,3的倍数各位上的数的和都是3的倍数。
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。
你发现的规律对三位数、四位数成立吗?找几个数来检验一下。
3×274=822,822是3的倍数,8+2+2=12
2016 年开了奥运会,2 + 0 + 1 + 6 = 9,是 3 的倍数,2016 = 3×672,确实是 3 的倍数,太神奇啦!
3×65=195,195是3的倍数,1+9+5=15
这几个数各个数位上的数字之和是3的倍数。
1.判断一个数是不是3的倍数,不能只看这个数个位上的数,而要看它各数位上的数的和。
2.在判断一个大数是不是3的倍数时,如果这个大数各数位上的数的和仍然很大,那么可以把加得的和的各数位上的数再相加,如果得到的结果是3的倍数,那么这个大数就是3的倍数,否则就不是。
1.一个数同时是2、3的倍数,这个数有什么特征
这个数的特征是:偶数,且各数位上的数的和是3的倍数。
3.一个数同时是2、3、5的倍数,这个数有什么特征
这个数的特征是:个位上是0或5,且各数位上的数的和是3的倍数。
2.一个数同时是3、5的倍数,这个数有什么特征
这个数的特征是:个位上是0,且各数位上的数的和是3的倍数。
课堂练习
2+4=6,6是3的倍数,所以24是3的倍数。增加的卡片可以是0。2+4+0=6,240是3的倍数。
下面用数字卡片摆出的数中,哪些是3的倍数?在每个数后面增加一张卡片,使这个三位数成为3的倍数。
2
4
5
8
4
6
9
6
还可以是3,6,9。2+4+3=9,243是3的倍数;2+4+6=12,246是3的倍数;2+4+9=15,249是3的倍数。
后面可以加0 3 6 9这些数字的卡片。
2
4
课堂练习
9+6=15,15是3的倍数,所以96是3的倍数。增加的卡片可以是0。9+6+0=15,960是3的倍数。
还可以是3,6,9。9+6+3=18,963是3的倍数;9+6+6=21,9666是3的倍数;9+6+9=24,969是3的倍数。
后面可以加0 3 6 9这些数字的卡片。
9
6
圈出3的倍数。
92 75 36 206 65 3051 779 9999
111 49 165 5988 655 131 2222 7203
判断一个数是不是3的倍数,不能只看这个数个位上的数,而要看它各数位上的数的和。如果得到的结果是3的倍数,那么这个大数就是3的倍数,否则就不是。
选出两个数字组成一个两位数,分别满足下面的条件。
0
3
4
5
(1)是3的倍数:
(2)同时是2和3的倍数:
(3)同时是3和5的倍数:
(4)同时是2、3和5的倍数:
30、45、54
30、54
45、30
30
你能说出3个是3的倍数的偶数吗?
你能说出3个是5的倍数的奇数吗?
3的倍数是偶数的有6,12,18。
5的倍数是奇数的有15,25,35。
答案不唯一,合理即可。
□7 4□2 □44 65□ 12□1
在□里填一个数字,使每个数都是3的倍数。
2
5
8
0
3
6
9
1
4
7
1
4
7
2
5
8
各有几种填法?
至少再来 2 个人才能正好分完。
3 个人一组,总人数应是3的倍数,
22 最少加 2 才是 3 的倍数。
现在有22名学生分组玩游戏,至少再来几名学生就可以正好3人一组
下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)个位是3、6、9的数一定是3的倍数。( )
×
(2)用2、4、9组成的三位数都是3的倍数 。 ( )
√
(3)一个三位数各个数位上的数字都相同,这个数一定是3的倍数 。 ( )
√
(4)连续三个自然数的和一定是3的倍数。 ( )
√
个位上必须是0,2,4,6,8。
既是2的倍数,又是3的倍数的最小三位数是
______,最大三位数是______。
各位上的数字之和必须是3的倍数。
102
996
2、3的倍数
个位上是0,2,4,6,8,且各个数位上的数字之和是3的倍数。
个位上必须是0,5。
既是5的倍数,又是3的倍数的最小两位数是
______,最大两位数是______。
各位上的数字之和必须是3的倍数。
30
75
3、5的倍数
个位上是0,5,且各个数位上的数字之和是3的倍数。
既是2和5的倍数,又是3的倍数的最小两位数
是______。
30
个位上必须是0。
各位上的数字之和必须是3的倍数。
2、3、5的倍数
个位上是0,且各个数位上的数字之和是3的倍数。
冬冬到文具店买日记本,日记本的单价已经看不清楚了,他买了3本同样的日记本,售货员阿姨说应付34元,冬冬认为不对。你能解释这是为什么吗?
因为冬冬买了3本同样的日记本,不管日记本的单价是多少,应付的钱都应该是3的倍数,而34不是3的倍数,所以冬冬认为不对。
课堂小结
同学们,今天的数学课你们有哪些收获呢?
