六年级下册数学人教版小升初专题复习——平面图形的测量(课件)
文档属性
| 名称 | 六年级下册数学人教版小升初专题复习——平面图形的测量(课件) |  | |
| 格式 | pptx | ||
| 文件大小 | 609.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 19:25:12 | ||
图片预览







文档简介
(共27张PPT)
平面图形的测量
平面图形的周长和面积的意义
1.周长:封闭图形一周的长度是它的周长。
2.面积:物体表面或围成的平面图形的大小。
温馨提示
封闭图形才有周长
平面图形的周长和面积的计算
周长和面积的计算公式
名称 图例 字母公式
长方形 C=2(a+b)
S=ab
正方形 C=4a
S=a2
平行四边形 S=ah
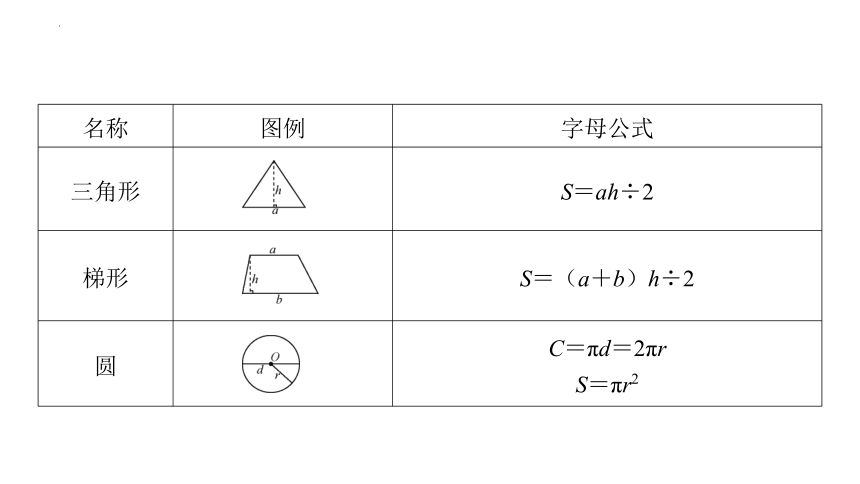
名称 图例 字母公式
三角形 S=ah÷2
梯形 S=(a+b)h÷2
圆 C=πd=2πr
S=πr2
温馨提示
1.三角形和平行四边形等底等高时,三角形的面积是平行四边形面积的
一半。
2.在运用公式进行周长和面积计算时,要注意单位统一。
温馨提示
计算三角形和梯形的高时,必须是面积的2倍除以底或上下底之和。
温馨提示
在同一个圆中,扇形的大小与这个扇形的圆心角度有关。S=πr2
(n°指圆心角的度数)。
组合图形面积的计算
计算组合图形的面积,可以把组合图形分解成几个已学过的图形,还可以通
过平移、割补、等量代换等方法解决问题。
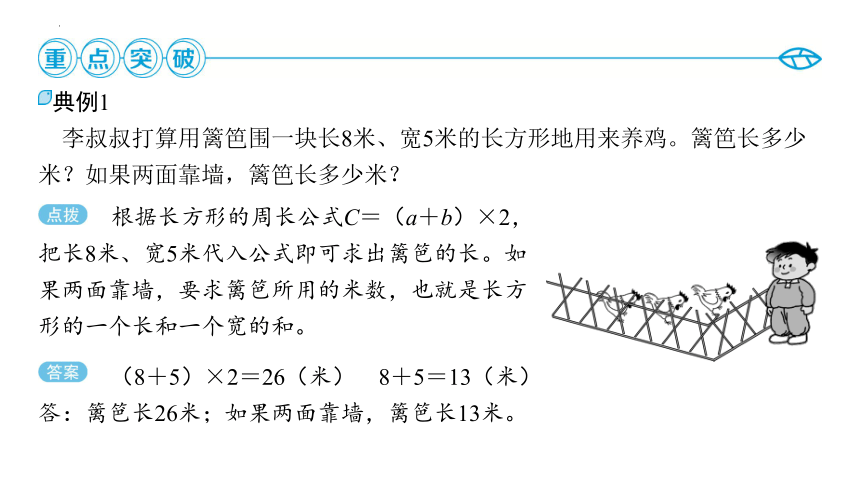
典例1
李叔叔打算用篱笆围一块长8米、宽5米的长方形地用来养鸡。篱笆长多少
米?如果两面靠墙,篱笆长多少米?
根据长方形的周长公式C=(a+b)×2,把长8米、宽5米代入公式即可求出篱笆的长。如果两面靠墙,要求篱笆所用的米数,也就是长方形的一个长和一个宽的和。
(8+5)×2=26(米) 8+5=13(米)
答:篱笆长26米;如果两面靠墙,篱笆长13米。
即时训练1:小猫每天上、下楼梯2个来回。小猫每天上、下楼梯要走多
少米?
【答案】36米
典例2
在一个长12厘米、宽8厘米的长方形中,剪下一个最大的圆。剩余部分的面
积是多少平方厘米?
本题考查长方形和圆的面积的计算以及知识间的相互关系。从条件可
知,在长为12厘米、宽为8厘米的长方形中剪下一个最大的圆,圆的直径就是
长方形的宽,这样可以求出圆的半径,进而求出圆的面积,再用长方形的面
积减去圆的面积,就可以得到剩余部分的面积。
圆的半径:8÷2=4(厘米)
圆的面积:3.14×42=50.24(平方厘米)
长方形的面积:12×8=96(平方厘米)
剩余部分的面积:96-50.24=45.76(平方厘米)
答:剩余部分的面积是45.76平方厘米。
即时训练2:在一个长6cm、宽4cm的长方形内剪下一个最大的半圆。这个半
圆的周长、面积分别是多少?
【答案】C:15.42cm S:14.13cm2
典例3
计算如图中的阴影部分的面积。(单位:cm)
图中阴影部分的面积我们可以这样求:上半部分的面积由半圆的面积
减去三角形的面积可得,下半部分的面积由梯形的面积减去半圆的面积可
得,上、下两部分面积之和即为所求。
将上半部分阴影割补如图:
(4×2+12)×4÷2-(4×2)×4÷2=24(cm2)
(方法不唯一)
即时训练3:如图,长方形与圆的面积相等,圆的周长是37.68cm,阴影部分
的面积是( 84.78 )cm2。
84.78
一、填空。
1.一个圆的周长是62.8厘米,它的面积是( 314 )平方厘米。
2.在面积是4平方分米的正方形内画一个最大的圆,则这个圆的周长是
( 6.28 )分米,面积是( 3.14 )平方分米。
3.如图中大平行四边形的面积是48dm2,A,B分别是上、下两边的中点,则阴
影部分的面积是( 24 )dm2。
第3题图
314
6.28
3.14
24
4.将一个周长是24厘米的长方形的宽增加2厘米,恰好可以得到一个正方形,
那么原来长方形的面积是( 35 )平方厘米。
5.一个平行四边形的面积是72平方米,与它等底等高的三角形的面积是
( 36 )平方米。
6.已知如图所示的长方形由10个小正方形拼成,其中阴影部分的面积占长方
形的( 30 )%;如果空白部分的面积是35平方厘米,那么长方形的面积
是( 50 )平方厘米。
第6题图
35
36
30
50
7.直径为8厘米的半圆的周长是( 20.56 )厘米,面积是( 25.12 )平
方厘米。
8.如图,一个直角三角形三条边分别是6cm、8cm、10cm,这个三角形斜边上
的高是( 4.8 )cm。
第8题图
20.56
25.12
4.8
9.如图,梯形的上底是6cm,下底是8cm,涂色部分的面积是24cm2,空白部
分的面积是( 32 )cm2。
第9题图
32
10.如图,平行四边形的面积是32cm2,图中甲、乙、丙三个三角形的面积比
是( 5∶2∶3 ),丙的面积是( 9.6 )cm2。
第10题图
5∶2∶3
9.6
二、判断。
1.等底等高的两个三角形,它们的周长一定相等。 ( × )
2.半圆的周长是所在圆周长的一半。 ( × )
3.两个面积相等的梯形一定能拼成一个平行四边形。 ( × )
4.圆的周长越长,面积就越大。 ( √ )
5.下面是三个相同的长方形,阴影部分的面积相等。 ( √ )
×
×
×
√
√
三、选择。
1.根据图中的数据,利用我们学过的面积公式不.能.算出面积的是( B )。
A. B. C.
B
2.正方形的边长扩大到原来的3倍,它的面积就扩大到原来的( C )倍。
A.3 B.6 C.9 D.不变
3.如图,大圆的半径是小圆半径的3倍,如果小圆沿着大圆的内测滚动一圈回
到原位,至少转了( B )圈。
A.2 B.3 C.6 D.9
4.用同样的铁丝分别围成长方形、正方形、等边三角形和圆,那么面积最大
的是( D )。
A.长方形 B.正方形 C.等边三角形 D.圆
C
B
D
5.如图,在正方形ABCD中,M,N分别为BC,CD的中点,则图中阴影部分面
积是正方形的( B )。
A. B.
C. D.
B
四、求下面图形的面积。(单位:cm)
【答案】117.5cm2
五、求阴影部分的面积。(单位:cm)
1. )
2.
【答案】42-3.14×22=3.44(cm2)
【答案】3.14×(122-82)=251.2(cm2)
六、解决问题。
1.把一根长40cm的铁丝围成一个长方形,长与宽的比是3∶2。它的面积
是多少?
【答案】40÷2=20(cm) 20×=12(cm) 20×=8(cm)
12×8=96(cm2)
2.乐乐和悠悠同时从圆形场地的同一地点出发,沿着场地的边相背而行(如
图),2分钟相遇。如果乐乐每分钟走88米,悠悠每分钟走69米,这个圆形场
地的周长是多少米?
【答案】(88+69)×2=314(米)
3.如图,把平行四边形分成甲、乙、丙三部分。如果乙的面积比丙少8cm2,
那么平行四边形的面积是多少?
【答案】8×2÷(6-4)=8(cm) (4+6)×8=80(cm2)
4.如图,一块长方形草地,长16m,宽10m。中间有两条1m宽的小路,这块草
地实际的种草面积有多少平方米?
【答案】(16-1)×(10-1)=135(m2)
5.如图,扇形的圆心角是45°,以扇形的一条边为直径画一个半圆,直径长10
厘米。计算阴影部分的面积。
【答案】面积:14.25平方厘米
平面图形的测量
平面图形的周长和面积的意义
1.周长:封闭图形一周的长度是它的周长。
2.面积:物体表面或围成的平面图形的大小。
温馨提示
封闭图形才有周长
平面图形的周长和面积的计算
周长和面积的计算公式
名称 图例 字母公式
长方形 C=2(a+b)
S=ab
正方形 C=4a
S=a2
平行四边形 S=ah
名称 图例 字母公式
三角形 S=ah÷2
梯形 S=(a+b)h÷2
圆 C=πd=2πr
S=πr2
温馨提示
1.三角形和平行四边形等底等高时,三角形的面积是平行四边形面积的
一半。
2.在运用公式进行周长和面积计算时,要注意单位统一。
温馨提示
计算三角形和梯形的高时,必须是面积的2倍除以底或上下底之和。
温馨提示
在同一个圆中,扇形的大小与这个扇形的圆心角度有关。S=πr2
(n°指圆心角的度数)。
组合图形面积的计算
计算组合图形的面积,可以把组合图形分解成几个已学过的图形,还可以通
过平移、割补、等量代换等方法解决问题。
典例1
李叔叔打算用篱笆围一块长8米、宽5米的长方形地用来养鸡。篱笆长多少
米?如果两面靠墙,篱笆长多少米?
根据长方形的周长公式C=(a+b)×2,把长8米、宽5米代入公式即可求出篱笆的长。如果两面靠墙,要求篱笆所用的米数,也就是长方形的一个长和一个宽的和。
(8+5)×2=26(米) 8+5=13(米)
答:篱笆长26米;如果两面靠墙,篱笆长13米。
即时训练1:小猫每天上、下楼梯2个来回。小猫每天上、下楼梯要走多
少米?
【答案】36米
典例2
在一个长12厘米、宽8厘米的长方形中,剪下一个最大的圆。剩余部分的面
积是多少平方厘米?
本题考查长方形和圆的面积的计算以及知识间的相互关系。从条件可
知,在长为12厘米、宽为8厘米的长方形中剪下一个最大的圆,圆的直径就是
长方形的宽,这样可以求出圆的半径,进而求出圆的面积,再用长方形的面
积减去圆的面积,就可以得到剩余部分的面积。
圆的半径:8÷2=4(厘米)
圆的面积:3.14×42=50.24(平方厘米)
长方形的面积:12×8=96(平方厘米)
剩余部分的面积:96-50.24=45.76(平方厘米)
答:剩余部分的面积是45.76平方厘米。
即时训练2:在一个长6cm、宽4cm的长方形内剪下一个最大的半圆。这个半
圆的周长、面积分别是多少?
【答案】C:15.42cm S:14.13cm2
典例3
计算如图中的阴影部分的面积。(单位:cm)
图中阴影部分的面积我们可以这样求:上半部分的面积由半圆的面积
减去三角形的面积可得,下半部分的面积由梯形的面积减去半圆的面积可
得,上、下两部分面积之和即为所求。
将上半部分阴影割补如图:
(4×2+12)×4÷2-(4×2)×4÷2=24(cm2)
(方法不唯一)
即时训练3:如图,长方形与圆的面积相等,圆的周长是37.68cm,阴影部分
的面积是( 84.78 )cm2。
84.78
一、填空。
1.一个圆的周长是62.8厘米,它的面积是( 314 )平方厘米。
2.在面积是4平方分米的正方形内画一个最大的圆,则这个圆的周长是
( 6.28 )分米,面积是( 3.14 )平方分米。
3.如图中大平行四边形的面积是48dm2,A,B分别是上、下两边的中点,则阴
影部分的面积是( 24 )dm2。
第3题图
314
6.28
3.14
24
4.将一个周长是24厘米的长方形的宽增加2厘米,恰好可以得到一个正方形,
那么原来长方形的面积是( 35 )平方厘米。
5.一个平行四边形的面积是72平方米,与它等底等高的三角形的面积是
( 36 )平方米。
6.已知如图所示的长方形由10个小正方形拼成,其中阴影部分的面积占长方
形的( 30 )%;如果空白部分的面积是35平方厘米,那么长方形的面积
是( 50 )平方厘米。
第6题图
35
36
30
50
7.直径为8厘米的半圆的周长是( 20.56 )厘米,面积是( 25.12 )平
方厘米。
8.如图,一个直角三角形三条边分别是6cm、8cm、10cm,这个三角形斜边上
的高是( 4.8 )cm。
第8题图
20.56
25.12
4.8
9.如图,梯形的上底是6cm,下底是8cm,涂色部分的面积是24cm2,空白部
分的面积是( 32 )cm2。
第9题图
32
10.如图,平行四边形的面积是32cm2,图中甲、乙、丙三个三角形的面积比
是( 5∶2∶3 ),丙的面积是( 9.6 )cm2。
第10题图
5∶2∶3
9.6
二、判断。
1.等底等高的两个三角形,它们的周长一定相等。 ( × )
2.半圆的周长是所在圆周长的一半。 ( × )
3.两个面积相等的梯形一定能拼成一个平行四边形。 ( × )
4.圆的周长越长,面积就越大。 ( √ )
5.下面是三个相同的长方形,阴影部分的面积相等。 ( √ )
×
×
×
√
√
三、选择。
1.根据图中的数据,利用我们学过的面积公式不.能.算出面积的是( B )。
A. B. C.
B
2.正方形的边长扩大到原来的3倍,它的面积就扩大到原来的( C )倍。
A.3 B.6 C.9 D.不变
3.如图,大圆的半径是小圆半径的3倍,如果小圆沿着大圆的内测滚动一圈回
到原位,至少转了( B )圈。
A.2 B.3 C.6 D.9
4.用同样的铁丝分别围成长方形、正方形、等边三角形和圆,那么面积最大
的是( D )。
A.长方形 B.正方形 C.等边三角形 D.圆
C
B
D
5.如图,在正方形ABCD中,M,N分别为BC,CD的中点,则图中阴影部分面
积是正方形的( B )。
A. B.
C. D.
B
四、求下面图形的面积。(单位:cm)
【答案】117.5cm2
五、求阴影部分的面积。(单位:cm)
1. )
2.
【答案】42-3.14×22=3.44(cm2)
【答案】3.14×(122-82)=251.2(cm2)
六、解决问题。
1.把一根长40cm的铁丝围成一个长方形,长与宽的比是3∶2。它的面积
是多少?
【答案】40÷2=20(cm) 20×=12(cm) 20×=8(cm)
12×8=96(cm2)
2.乐乐和悠悠同时从圆形场地的同一地点出发,沿着场地的边相背而行(如
图),2分钟相遇。如果乐乐每分钟走88米,悠悠每分钟走69米,这个圆形场
地的周长是多少米?
【答案】(88+69)×2=314(米)
3.如图,把平行四边形分成甲、乙、丙三部分。如果乙的面积比丙少8cm2,
那么平行四边形的面积是多少?
【答案】8×2÷(6-4)=8(cm) (4+6)×8=80(cm2)
4.如图,一块长方形草地,长16m,宽10m。中间有两条1m宽的小路,这块草
地实际的种草面积有多少平方米?
【答案】(16-1)×(10-1)=135(m2)
5.如图,扇形的圆心角是45°,以扇形的一条边为直径画一个半圆,直径长10
厘米。计算阴影部分的面积。
【答案】面积:14.25平方厘米
同课章节目录
