六年级下册数学人教版小升初专题复习-立体图形的认识与测量(课件)(共28张)
文档属性
| 名称 | 六年级下册数学人教版小升初专题复习-立体图形的认识与测量(课件)(共28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 580.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
立体图形的认识与测量
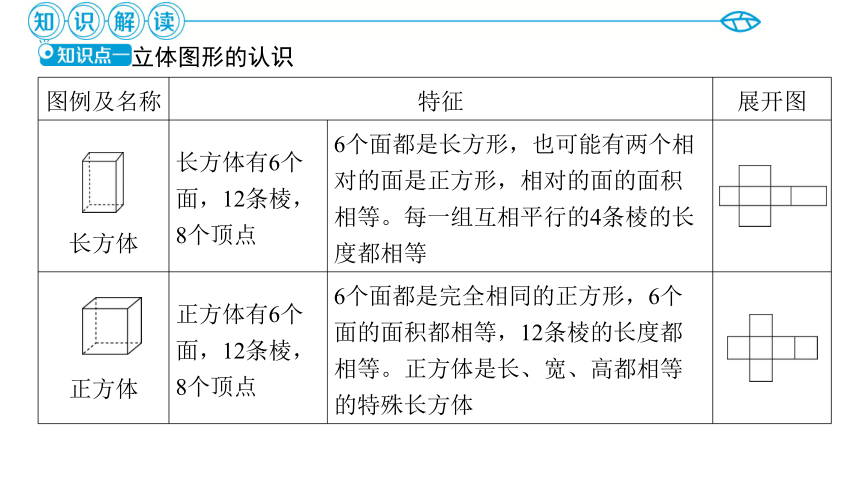
图例及名称 特征 展开图
长方体 长方体有6个
面,12条棱,
8个顶点 6个面都是长方形,也可能有两个相
对的面是正方形,相对的面的面积
相等。每一组互相平行的4条棱的长
度都相等
正方体 正方体有6个
面,12条棱,
8个顶点 6个面都是完全相同的正方形,6个
面的面积都相等,12条棱的长度都
相等。正方体是长、宽、高都相等
的特殊长方体
立体图形的认识
图例及名称 特征 展开图
圆柱 有3个面,上、下两个底面是面积相等的两个圆,侧
面是一个曲面,沿高展开是一个长方形或正方形,
长是圆柱的底面周长,宽是圆柱的高,圆柱有无数
条高
圆锥 圆锥的底面是一个圆,侧面是一个曲面,侧面展开
图是扇形。从圆锥的顶点到底面圆心的距离是圆锥
的高,圆锥只有一条高
温馨提示
1.正方体是特殊的长方体,是长、宽、高相等的长方体。
2.以长方形的一条边所在的直线为轴旋转一周可以形成一个圆柱。
3.以直角三角形的直角边所在的直线为轴旋转一周可以形成一个圆锥。
立体图形的表面积和体积
1.表面积:物体表面面积的总和,叫物体的表面积。
体积:物体所占空间的大小,叫物体的体积。
容积:箱子、油桶、仓库等所能容纳物体的体积,通常叫它们的容积。
体积与容积单位之间的换算。1 L=1 dm3 1 mL=1 cm3
2.长方体的表面积=(长×宽+长×高+宽×高)×2
S表=2(ab+ah+bh)
长方体的体积=长×宽×高 V=abh
正方体的表面积=棱长×棱长×6 S表=6a2
正方体的体积=棱长×棱长×棱长 V=a×a×a=a3
圆柱的表面积=侧面积+底面积×2
圆柱的侧面积=底面周长×高
圆柱的体积=底面积×高 V=Sh
圆锥的体积=×底面积×高 V=Sh
3.不规则物体的体积:把不规则物体完全浸入规则容器的水中,观察此时水
面的高度,然后根据规则物体的体积计算公式计算出水面上升部分的体积,
就是不规则物体的体积。
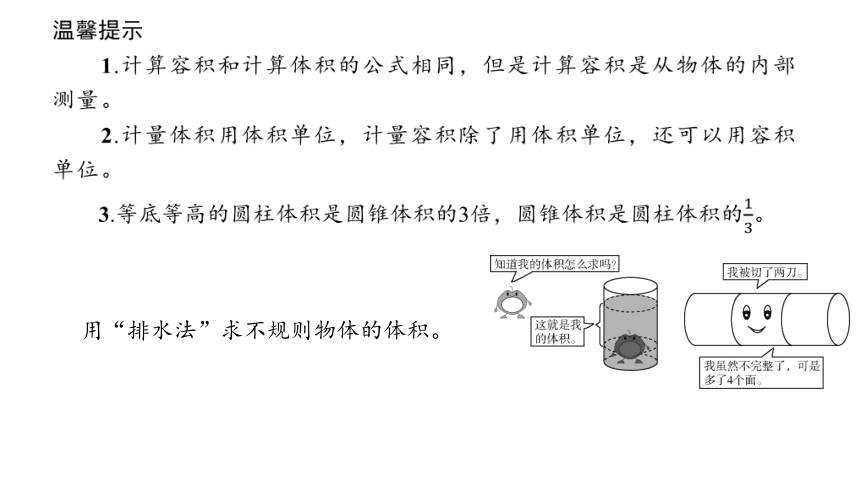
温馨提示
1.计算容积和计算体积的公式相同,但是计算容积是从物体的内部
测量。
2.计量体积用体积单位,计量容积除了用体积单位,还可以用容积
单位。
3.等底等高的圆柱体积是圆锥体积的3倍,圆锥体积是圆柱体积的。
用“排水法”求不规则物体的体积。
立体图形的切割与拼组
观察物体
在实际生活中,我们常常需要对一个物体从不同角度、方向进行观察,从而
获得其形状、大小、颜色等各方面的信息。
从不同角度、方向观察物体,常常会得到不同的结果。
温馨提示
观察物体一次最多只能看到三个面。
典例1
右面是一个立体图形的展开图。(单位:厘米)
(1)这个展开图可以折成 体。
(2)折成立体图形后长度是5厘米的棱有 条。
(3)棱长总和是 。
此题考查的是长方体与其展开图的关系,观图可知,这是一个有两个
相对的面是正方形的长方体,正方形的边长是2厘米,长方体的高是5厘米。
(1)长方 (2)4 (3)36厘米
即时训练1:下面( A )图是圆柱的展开图。
A. B. C.
A
典例2
一个长方体铁皮油箱长80厘米、宽50厘米、高40厘米。
(1)做这个油箱至少要用铁皮多少平方分米?
(2)这个油箱的容积是多少升?(铁皮的厚度忽略不计)
(1)要求做这个油箱至少要用铁皮多少平方分米,就是求这个长方体
铁皮油箱的表面积,可直接利用公式计算,计算时注意单位换算。
(2)求这个油箱的容积就相当于求这个油箱的体积。
(1)(80×50+80×40+50×40)×2
=18400(平方厘米)
=184(平方分米)
(2)80×50×40=160000(立方厘米)=160(立方分米)=160(升)
即时训练2:一个圆柱形鱼缸,底面直径是6dm,高是35cm,里面盛了一些
水,把一个底面半径为20cm的圆锥放入鱼缸中(圆锥全部浸入水中),鱼缸
中的水面升高了2cm。这个圆锥的高是多少?
【答案】3.14×(6×10÷2)2×2=5652(cm3)
5652÷(×3.14×202)=13.5(cm)
典例3
求下面组合图形的表面积和体积。(单位:cm)
大圆柱的上底环形面与小圆柱的上底面正好可以拼成大圆柱的上底
面。因此,组合图形的表面积等于大圆柱的表面积加小圆柱的侧面积。组合
图形的体积等于大圆柱体积加小圆柱体积。
S表:3.14×8×5+3.14×(8÷2)2×2+3.14×6×3=282.6(cm2)
V:3.14×(8÷2)2×5+3.14×(6÷2)2×3=335.98(cm3)
即时训练3:有一个正方体木块,在其内部挖去一个长方体(如图)。剩下木
块的表面积是多少平方厘米?体积呢?(单位:cm)
【答案】S:700cm2 V:880cm3
典例4
观察如图,从左面看到的图形是( ),从上面看到的图形是
( )。
从左面看有两层:下层2个正方形,上层1个正方形。从上面看到的图
形也是两层,分别是3个正方形和1个正方形。
即时训练4:一个立体图形是由5个相同的正方体搭成的,从正面看到的平面
图形是 ,从右面看到的平面图形是 ,这个立体图形可能是
( C )。
A. B. C.
C
一、填空。
1.等底等高的圆柱和圆锥,已知圆柱的体积比圆锥多8dm3,则圆柱的体积是
( 12dm3 ),圆锥的体积是( 4dm3 )。
2.一个正方体的棱长总和是24cm,它的表面积是( 24cm2 ),体积是
( 8cm3 )。
3.如图中直角三角形以4cm的直角边为轴旋转一周,可以得到一个( 圆
锥 ),这个图形的高是( 4cm ),底面半径是( 6cm ),体积是
( 150.72cm3 )。
12dm3
4dm3
24cm2
8cm3
圆
锥
4cm
6cm
150.72cm3
4.用12个棱长为1分米的正方体拼成一个长方体,拼成的长方体的表面积最小
是( 32 )平方分米,最大是( 50 )平方分米。
5.一个用小正方体搭成的立体图形,淘淘从正面看到的是 ,从上面看到
的是 ,那么搭成这样一个立体图形最少要( 5 )个小正方体,最多
要( 6 )个小正方体。
6.把一根半径为2dm,长为1m的圆木平均截成2根圆木,表面积增加
( 25.12 )dm2。
7.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米。一位同学去水
池洗手,走时忘记关掉水龙头,5分钟浪费( 7.536 )升水。
8.学校体育馆底层用10根圆柱体柱子支撑着,每根柱子高3m,底面直径
5dm,油漆这些柱子的面积是( 47.1 )m2。
32
50
5
6
25.12
7.536
47.1
二、判断。
1.长方体(不是正方体)最多有4个面的面积相等。 ( √ )
2.棱长是6cm的正方体,它的表面积和体积相等。 ( × )
3.圆锥的体积是圆柱体积的。 ( × )
4.等底等高的长方体和圆柱,它们的体积一定相等。 ( √ )
5.一个长方体,它的长、宽、高都扩大到原来的2倍,它的体积就扩大到原来
的6倍。 ( × )
√
×
×
√
×
三、选择。
1.一个长方体的棱长之和是36cm,相交于一个顶点的所有棱长之和是
( A )。
A.9cm B.12cm C.18cm D.36cm
2.下面4个图形中是左边盒子的展开图的是( A )。
A. B. C. D.
A
A
3.下面能旋转成圆柱的图形是( A )。
A. B. C. D.
4.把一个长方体的长、宽、高各削去后,体积是原来的( C )。
A. B. C. D.
A
C
5.如图,甲的体积( A )乙的体积,甲的表面积( C )乙的表面积。
A.> B.< C.=
6.把一个圆柱削成一个最大的圆锥,削去部分的体积是圆锥的( C )。
A. B. C.2倍 D.3倍
A
C
C
四、按要求计算。
1.计算下面图形的表面积。(单位:cm)
【答案】3.14×(6÷2)2×2+3.14×6×8=207.24(cm2)
2.计算下面各图形的体积。
(1)
【答案】3.14×52×3+×3.14×52×3=314(m3)
(2) (单位:cm)
【答案】30×20×5-3.14×()2×5=2607.5(cm3)
五、解决问题。
1.一个长方体铁块,长6.28厘米,宽5厘米,高6厘米,现在把这个铁块熔铸成
一个圆柱体,圆柱的底面积是18.84平方厘米。圆柱的高是多少厘米?
【答案】10厘米
2.一个圆锥形小麦堆,底面周长是6.28米,高是1.5米。如果每立方米小麦重
750千克,这堆小麦重多少千克?
【答案】1177.5千克
3.一个盖着瓶盖的瓶子里装有一些水(如图),请你根据图中标明的数据,
计算瓶子的容积。
【答案】60mL
4.一个圆柱形容器中装有水,先把一个棱长为6cm的正方体铁块浸没在水中,
水面上升了5cm,再把一个圆锥形铅锤浸没在水中,水面又上升了3cm。这个
铅锤的体积是多少?(水没有溢出)
【答案】6×6×6÷5×3=129.6(cm3)
5.如图,正方体的体积是360立方厘米,把它削成一个最大的圆锥。这个圆锥
的体积是多少立方厘米?
【答案】设正方体的棱长为a厘米。体积为a3立方厘米,即a3=360,圆锥的
体积=×π×()2×a=π×a3=×3.14×360=94.2(立方厘米)
立体图形的认识与测量
图例及名称 特征 展开图
长方体 长方体有6个
面,12条棱,
8个顶点 6个面都是长方形,也可能有两个相
对的面是正方形,相对的面的面积
相等。每一组互相平行的4条棱的长
度都相等
正方体 正方体有6个
面,12条棱,
8个顶点 6个面都是完全相同的正方形,6个
面的面积都相等,12条棱的长度都
相等。正方体是长、宽、高都相等
的特殊长方体
立体图形的认识
图例及名称 特征 展开图
圆柱 有3个面,上、下两个底面是面积相等的两个圆,侧
面是一个曲面,沿高展开是一个长方形或正方形,
长是圆柱的底面周长,宽是圆柱的高,圆柱有无数
条高
圆锥 圆锥的底面是一个圆,侧面是一个曲面,侧面展开
图是扇形。从圆锥的顶点到底面圆心的距离是圆锥
的高,圆锥只有一条高
温馨提示
1.正方体是特殊的长方体,是长、宽、高相等的长方体。
2.以长方形的一条边所在的直线为轴旋转一周可以形成一个圆柱。
3.以直角三角形的直角边所在的直线为轴旋转一周可以形成一个圆锥。
立体图形的表面积和体积
1.表面积:物体表面面积的总和,叫物体的表面积。
体积:物体所占空间的大小,叫物体的体积。
容积:箱子、油桶、仓库等所能容纳物体的体积,通常叫它们的容积。
体积与容积单位之间的换算。1 L=1 dm3 1 mL=1 cm3
2.长方体的表面积=(长×宽+长×高+宽×高)×2
S表=2(ab+ah+bh)
长方体的体积=长×宽×高 V=abh
正方体的表面积=棱长×棱长×6 S表=6a2
正方体的体积=棱长×棱长×棱长 V=a×a×a=a3
圆柱的表面积=侧面积+底面积×2
圆柱的侧面积=底面周长×高
圆柱的体积=底面积×高 V=Sh
圆锥的体积=×底面积×高 V=Sh
3.不规则物体的体积:把不规则物体完全浸入规则容器的水中,观察此时水
面的高度,然后根据规则物体的体积计算公式计算出水面上升部分的体积,
就是不规则物体的体积。
温馨提示
1.计算容积和计算体积的公式相同,但是计算容积是从物体的内部
测量。
2.计量体积用体积单位,计量容积除了用体积单位,还可以用容积
单位。
3.等底等高的圆柱体积是圆锥体积的3倍,圆锥体积是圆柱体积的。
用“排水法”求不规则物体的体积。
立体图形的切割与拼组
观察物体
在实际生活中,我们常常需要对一个物体从不同角度、方向进行观察,从而
获得其形状、大小、颜色等各方面的信息。
从不同角度、方向观察物体,常常会得到不同的结果。
温馨提示
观察物体一次最多只能看到三个面。
典例1
右面是一个立体图形的展开图。(单位:厘米)
(1)这个展开图可以折成 体。
(2)折成立体图形后长度是5厘米的棱有 条。
(3)棱长总和是 。
此题考查的是长方体与其展开图的关系,观图可知,这是一个有两个
相对的面是正方形的长方体,正方形的边长是2厘米,长方体的高是5厘米。
(1)长方 (2)4 (3)36厘米
即时训练1:下面( A )图是圆柱的展开图。
A. B. C.
A
典例2
一个长方体铁皮油箱长80厘米、宽50厘米、高40厘米。
(1)做这个油箱至少要用铁皮多少平方分米?
(2)这个油箱的容积是多少升?(铁皮的厚度忽略不计)
(1)要求做这个油箱至少要用铁皮多少平方分米,就是求这个长方体
铁皮油箱的表面积,可直接利用公式计算,计算时注意单位换算。
(2)求这个油箱的容积就相当于求这个油箱的体积。
(1)(80×50+80×40+50×40)×2
=18400(平方厘米)
=184(平方分米)
(2)80×50×40=160000(立方厘米)=160(立方分米)=160(升)
即时训练2:一个圆柱形鱼缸,底面直径是6dm,高是35cm,里面盛了一些
水,把一个底面半径为20cm的圆锥放入鱼缸中(圆锥全部浸入水中),鱼缸
中的水面升高了2cm。这个圆锥的高是多少?
【答案】3.14×(6×10÷2)2×2=5652(cm3)
5652÷(×3.14×202)=13.5(cm)
典例3
求下面组合图形的表面积和体积。(单位:cm)
大圆柱的上底环形面与小圆柱的上底面正好可以拼成大圆柱的上底
面。因此,组合图形的表面积等于大圆柱的表面积加小圆柱的侧面积。组合
图形的体积等于大圆柱体积加小圆柱体积。
S表:3.14×8×5+3.14×(8÷2)2×2+3.14×6×3=282.6(cm2)
V:3.14×(8÷2)2×5+3.14×(6÷2)2×3=335.98(cm3)
即时训练3:有一个正方体木块,在其内部挖去一个长方体(如图)。剩下木
块的表面积是多少平方厘米?体积呢?(单位:cm)
【答案】S:700cm2 V:880cm3
典例4
观察如图,从左面看到的图形是( ),从上面看到的图形是
( )。
从左面看有两层:下层2个正方形,上层1个正方形。从上面看到的图
形也是两层,分别是3个正方形和1个正方形。
即时训练4:一个立体图形是由5个相同的正方体搭成的,从正面看到的平面
图形是 ,从右面看到的平面图形是 ,这个立体图形可能是
( C )。
A. B. C.
C
一、填空。
1.等底等高的圆柱和圆锥,已知圆柱的体积比圆锥多8dm3,则圆柱的体积是
( 12dm3 ),圆锥的体积是( 4dm3 )。
2.一个正方体的棱长总和是24cm,它的表面积是( 24cm2 ),体积是
( 8cm3 )。
3.如图中直角三角形以4cm的直角边为轴旋转一周,可以得到一个( 圆
锥 ),这个图形的高是( 4cm ),底面半径是( 6cm ),体积是
( 150.72cm3 )。
12dm3
4dm3
24cm2
8cm3
圆
锥
4cm
6cm
150.72cm3
4.用12个棱长为1分米的正方体拼成一个长方体,拼成的长方体的表面积最小
是( 32 )平方分米,最大是( 50 )平方分米。
5.一个用小正方体搭成的立体图形,淘淘从正面看到的是 ,从上面看到
的是 ,那么搭成这样一个立体图形最少要( 5 )个小正方体,最多
要( 6 )个小正方体。
6.把一根半径为2dm,长为1m的圆木平均截成2根圆木,表面积增加
( 25.12 )dm2。
7.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米。一位同学去水
池洗手,走时忘记关掉水龙头,5分钟浪费( 7.536 )升水。
8.学校体育馆底层用10根圆柱体柱子支撑着,每根柱子高3m,底面直径
5dm,油漆这些柱子的面积是( 47.1 )m2。
32
50
5
6
25.12
7.536
47.1
二、判断。
1.长方体(不是正方体)最多有4个面的面积相等。 ( √ )
2.棱长是6cm的正方体,它的表面积和体积相等。 ( × )
3.圆锥的体积是圆柱体积的。 ( × )
4.等底等高的长方体和圆柱,它们的体积一定相等。 ( √ )
5.一个长方体,它的长、宽、高都扩大到原来的2倍,它的体积就扩大到原来
的6倍。 ( × )
√
×
×
√
×
三、选择。
1.一个长方体的棱长之和是36cm,相交于一个顶点的所有棱长之和是
( A )。
A.9cm B.12cm C.18cm D.36cm
2.下面4个图形中是左边盒子的展开图的是( A )。
A. B. C. D.
A
A
3.下面能旋转成圆柱的图形是( A )。
A. B. C. D.
4.把一个长方体的长、宽、高各削去后,体积是原来的( C )。
A. B. C. D.
A
C
5.如图,甲的体积( A )乙的体积,甲的表面积( C )乙的表面积。
A.> B.< C.=
6.把一个圆柱削成一个最大的圆锥,削去部分的体积是圆锥的( C )。
A. B. C.2倍 D.3倍
A
C
C
四、按要求计算。
1.计算下面图形的表面积。(单位:cm)
【答案】3.14×(6÷2)2×2+3.14×6×8=207.24(cm2)
2.计算下面各图形的体积。
(1)
【答案】3.14×52×3+×3.14×52×3=314(m3)
(2) (单位:cm)
【答案】30×20×5-3.14×()2×5=2607.5(cm3)
五、解决问题。
1.一个长方体铁块,长6.28厘米,宽5厘米,高6厘米,现在把这个铁块熔铸成
一个圆柱体,圆柱的底面积是18.84平方厘米。圆柱的高是多少厘米?
【答案】10厘米
2.一个圆锥形小麦堆,底面周长是6.28米,高是1.5米。如果每立方米小麦重
750千克,这堆小麦重多少千克?
【答案】1177.5千克
3.一个盖着瓶盖的瓶子里装有一些水(如图),请你根据图中标明的数据,
计算瓶子的容积。
【答案】60mL
4.一个圆柱形容器中装有水,先把一个棱长为6cm的正方体铁块浸没在水中,
水面上升了5cm,再把一个圆锥形铅锤浸没在水中,水面又上升了3cm。这个
铅锤的体积是多少?(水没有溢出)
【答案】6×6×6÷5×3=129.6(cm3)
5.如图,正方体的体积是360立方厘米,把它削成一个最大的圆锥。这个圆锥
的体积是多少立方厘米?
【答案】设正方体的棱长为a厘米。体积为a3立方厘米,即a3=360,圆锥的
体积=×π×()2×a=π×a3=×3.14×360=94.2(立方厘米)
同课章节目录
