8.3完全平方公式与平方差公式导学案
图片预览


文档简介
与儿街中学有效教学导学案
年级:七年级 学科:数学 课型:新授课 课时:三 课时 主备:孙继平、吴正国 审核:周先会、张学东 时间:2009年 4月 1日
课题:8.3完全平方公式与平方差公式
一、学习目标
1.通过探索完全平方公式与平方差公式,培养自己观察、交流、归纳、猜测、验证能力。
2.会推导乘法公式,了解公式的几何背景,会用公式计算。
3.试着体会数形结合的数学思想和方法。
二、重点难点
1.重点:乘法公式的应用。
2.难点:公式的结构特征以及对公式中字母所表示广泛含义的理解和正确运用。
三、预习导学
第一课时(完全平方公式)
一、本节目标:1.理解并掌握完全平方公式。
2.会运用完全平方公式解决一些简单的习题。
二、导学:
1.复习回顾:
计算下列各式,你能发现什么规律?
(1)(p+1)2=(p+1)(p+1)= ;
(2)(m+2)2= ;
(3)(p-1)2=(p-1)(p-1)= ;
(4)(m-2)2= .
2.尝试归纳:
3.完全平方公式用语言叙述是:
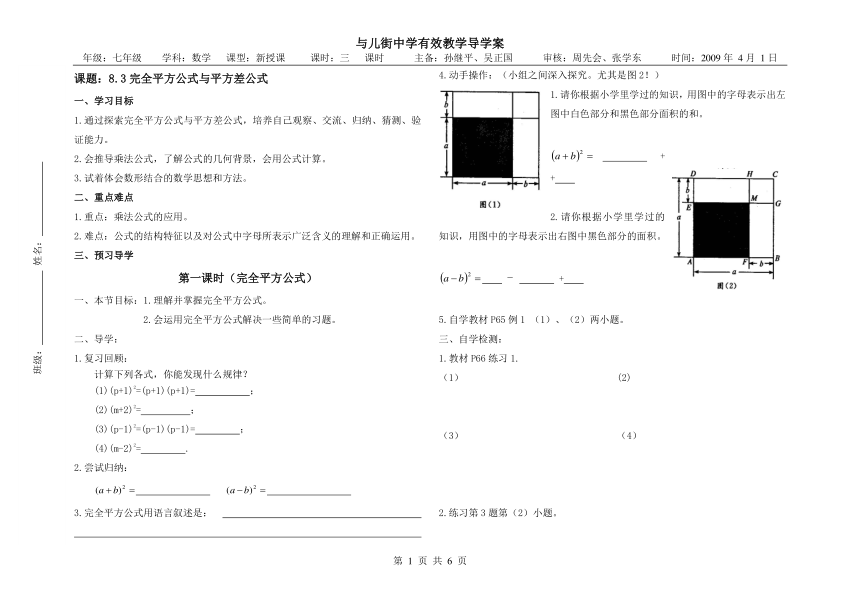
4.动手操作:(小组之间深入探究。尤其是图2!)
1.请你根据小学里学过的知识,用图中的字母表示出左图中白色部分和黑色部分面积的和。
+ +
2.请你根据小学里学过的知识,用图中的字母表示出右图中黑色部分的面积。
- +
5.自学教材P65例1 (1)、(2)两小题。
三、自学检测:
1.教材P66练习1.
(1) (2)
(3) (4)
2.练习第3题第(2)小题。
3. 应用完全平方公式计算:
(1)(4m+n)2 (2)(y-)2
(3)(-a-b)2 (4)(b-a)2
(5)1022 (6)992
四、课堂检测:
1.教材P67习题8.3 1.计算:
(1) (2)
2. 教材P67习题8.3 第8题。
五、拓展训练:(为综合运用做准备。)
1.填空题
(1)(-3x+4y)2=_________.
(2)(-2a-b)2=_________.
(3)x2-4xy+________=(x-2y)2.
(4)a2+b2=(a+b)2+_________.
(5)a2+______+9b2=(a+3b)2.
(6)(a-2b)2 +(a+2b)2=_________.
2.选择题
(1)下列计算正确的是( )
A.(m-1)2=m2-1 B.(x+1)(x+1)=x2+x+1
C.(x-y)2=x2-xy-y2 D.(x+y)(x-y)(x2-y2)=x4-y4
(2)如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(3)将正方形的边长由acm增加6cm,则正方形的面积增加了( )
A.36cm2 B.12acm2 C.(36+12a)cm2 D.以上都不对
3.用乘法公式计算
(1)(x -y)2
(2)(x2-2y2)2-(x2+2y2)2
(3)29×31×(302+1)
第二课时(平方差公式)
一、本节目标:1.理解并掌握平方差公式。
2.会运用平方差公式解决一些简单的习题。
二、导学:
1.复习回顾:
计算下列各式,你能发现什么规律?
(1)(x+1)(x-1)=
(2)(m+2)(m-2)=
(3)(2x+1)(2x-1)=
(4)(x+5y)(x-5y)=
2.尝试归纳:
3.平方差公式用语言叙述是:
4.动手操作:请你用小学里学过的知识,用图中的字母表示出第一个图中两个梯形的面积之和。
5.自学教材P65例1第(3)小题、例2的第(1)小题。
三、自学检测:
1.教材P66练习 2.利用乘法公式计算:
(1) (2)
(3) (4)
2. 教材P66练习第3题第(1)小题。
3.利用平方差公式计算:
(1)(a+b)(-b+a) (2)(-a-b)(a-b)
(3)(3a+2b)(3a-2b) (4)(a5-b2)(a5+b2)
四、课堂检测:
1.教材P67习题8.3 2.计算:(做题时要特别小心。)
(1) (2)
(3) (4)
第三课时(乘法公式的综合运用)
一、本节目标:1.进一步理解乘法公式。
2.能熟练地运用乘法公式解题。
二、导学:
1.复习回顾两个公式。
2.自学例题:教材P65例2第(2)小题、P66例3.(注意书上的解题方法。)
3.注意:本节内容偏难,小组内、小组间要认真交流,有困难的要问老师。
三、自学检测:
1.教材P66练习第4 题:
2.教材P66练习第5题:
(1) (2)
3.教材P67习题8.3 3.计算:
(1) (2)
(3) (4)
四、课堂检测:
1. 教材P67习题8.3 4.先化简,再求值:
2. 教材P67习题8.3 5.解方程:
(1) (2)
3. 教材P67习题8.3 6.解不等式:
4.教材P67习题8.3 第7题。
5. 教材P67习题8.3 10.计算:
(1) (2)
自我评价 知识巩固
1.(2004·青海)下列各式中,相等关系一定成立的是( )
A.(x-y)2=(y-x)2 B.(x+6)(x-6)=x2-6
C.(x+y)2=x2+y2 D.6(x-2)+x(2-x)=(x-2)(x-6)
2.(2003·泰州)下列运算正确的是( )
A.x2+x2=2x4 B.a2·a3= a5
C.(-2x2)4=16x6 D.(x+3y)(x-3y)=x2-3y2
3.(2003·河南)下列计算正确的是( )
A.(-4x)·(2x2+3x-1)=-8x3-12x2-4x
B.(x+y)(x2+y2)=x3+y3
C.(-4a-1)(4a-1)=1-16a2
D.(x-2y)2=x2-2xy+4y2
4.(x+2)(x-2)(x2+4)的计算结果是( )
A.x4+16 B.-x4-16 C.x4-16 D.16-x4
5.19922-1991×1993的计算结果是( )
A.1 B.-1 C.2 D.-2
6.对于任意的整数n,能整除代数式(n+3)(n-3)-(n+2)(n-2)的整数是( )
A.4 B.3 C.5 D.2
7.( )(5a+1)=1-25a2,(2x-3) =4x2-9,(-2a2-5b)( )=4a4-25b2
8.99×101=( )( )= .
9.(x-y+z)(-x+y+z)=[z+( )][ ]=z2-( )2.
10.多项式x2+kx+25是另一个多项式的平方,则k= .
11.(a+b)2=(a-b)2+ ,a2+b2=[(a+b)2+(a-b)2]( ),
a2+b2=(a+b)2+ ,a2+b2=(a-b)2+ .
12.计算.
(1)(a+b)2-(a-b)2; (2)(3x-4y)2-(3x+y)2;
(3)(2x+3y)2-(4x-9y)(4x+9y)+(2x-3y)2;
(4)1.23452+0.76552+2.469×0.7655;
(5)(x+2y)(x-y)-(x+y)2.
13.已知m2+n2-6m+10n+34=0,求m+n的值
14.已知a+=4,求a2+和a4+的值.
15.已知(t+58)2=654481,求(t+84)(t+68)的值.
16.解不等式(1-3x)2+(2x-1)2>13(x-1)(x+1).
17.已知a=1990x+1989,b=1990x+1990,c=1990x+1991,求a2+b2+c2-ab-ac-bc的值.
18.(2003·郑州)如果(2a+2b+1)(2a+2b-1)=63,求a+b的值.
19.已知(a+b)2=60,(a-b)2=80,求a2+b2及ab的值.
20.化简(x+y)+(2x+)+(3x+)+…+(9x+),并求当x=2,y=9时的值.
21.若f(x)=2x-1(如f(-2)=2×(-2)-1,f(3)=2×3-1),求的值.
22.观察下面各式:
12+(1×2)2+22=(1×2+1)2
22+(2×3)2+32=(2×3+1)2
32+(3×4)2+42=(3×4+1)2
……
(1)写出第2005个式子;
(2)写出第n个式子,并说明你的结论.
班级: 姓名:
班级: 姓名:
班级: 姓名:
第 6 页 共 6 页
年级:七年级 学科:数学 课型:新授课 课时:三 课时 主备:孙继平、吴正国 审核:周先会、张学东 时间:2009年 4月 1日
课题:8.3完全平方公式与平方差公式
一、学习目标
1.通过探索完全平方公式与平方差公式,培养自己观察、交流、归纳、猜测、验证能力。
2.会推导乘法公式,了解公式的几何背景,会用公式计算。
3.试着体会数形结合的数学思想和方法。
二、重点难点
1.重点:乘法公式的应用。
2.难点:公式的结构特征以及对公式中字母所表示广泛含义的理解和正确运用。
三、预习导学
第一课时(完全平方公式)
一、本节目标:1.理解并掌握完全平方公式。
2.会运用完全平方公式解决一些简单的习题。
二、导学:
1.复习回顾:
计算下列各式,你能发现什么规律?
(1)(p+1)2=(p+1)(p+1)= ;
(2)(m+2)2= ;
(3)(p-1)2=(p-1)(p-1)= ;
(4)(m-2)2= .
2.尝试归纳:
3.完全平方公式用语言叙述是:
4.动手操作:(小组之间深入探究。尤其是图2!)
1.请你根据小学里学过的知识,用图中的字母表示出左图中白色部分和黑色部分面积的和。
+ +
2.请你根据小学里学过的知识,用图中的字母表示出右图中黑色部分的面积。
- +
5.自学教材P65例1 (1)、(2)两小题。
三、自学检测:
1.教材P66练习1.
(1) (2)
(3) (4)
2.练习第3题第(2)小题。
3. 应用完全平方公式计算:
(1)(4m+n)2 (2)(y-)2
(3)(-a-b)2 (4)(b-a)2
(5)1022 (6)992
四、课堂检测:
1.教材P67习题8.3 1.计算:
(1) (2)
2. 教材P67习题8.3 第8题。
五、拓展训练:(为综合运用做准备。)
1.填空题
(1)(-3x+4y)2=_________.
(2)(-2a-b)2=_________.
(3)x2-4xy+________=(x-2y)2.
(4)a2+b2=(a+b)2+_________.
(5)a2+______+9b2=(a+3b)2.
(6)(a-2b)2 +(a+2b)2=_________.
2.选择题
(1)下列计算正确的是( )
A.(m-1)2=m2-1 B.(x+1)(x+1)=x2+x+1
C.(x-y)2=x2-xy-y2 D.(x+y)(x-y)(x2-y2)=x4-y4
(2)如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(3)将正方形的边长由acm增加6cm,则正方形的面积增加了( )
A.36cm2 B.12acm2 C.(36+12a)cm2 D.以上都不对
3.用乘法公式计算
(1)(x -y)2
(2)(x2-2y2)2-(x2+2y2)2
(3)29×31×(302+1)
第二课时(平方差公式)
一、本节目标:1.理解并掌握平方差公式。
2.会运用平方差公式解决一些简单的习题。
二、导学:
1.复习回顾:
计算下列各式,你能发现什么规律?
(1)(x+1)(x-1)=
(2)(m+2)(m-2)=
(3)(2x+1)(2x-1)=
(4)(x+5y)(x-5y)=
2.尝试归纳:
3.平方差公式用语言叙述是:
4.动手操作:请你用小学里学过的知识,用图中的字母表示出第一个图中两个梯形的面积之和。
5.自学教材P65例1第(3)小题、例2的第(1)小题。
三、自学检测:
1.教材P66练习 2.利用乘法公式计算:
(1) (2)
(3) (4)
2. 教材P66练习第3题第(1)小题。
3.利用平方差公式计算:
(1)(a+b)(-b+a) (2)(-a-b)(a-b)
(3)(3a+2b)(3a-2b) (4)(a5-b2)(a5+b2)
四、课堂检测:
1.教材P67习题8.3 2.计算:(做题时要特别小心。)
(1) (2)
(3) (4)
第三课时(乘法公式的综合运用)
一、本节目标:1.进一步理解乘法公式。
2.能熟练地运用乘法公式解题。
二、导学:
1.复习回顾两个公式。
2.自学例题:教材P65例2第(2)小题、P66例3.(注意书上的解题方法。)
3.注意:本节内容偏难,小组内、小组间要认真交流,有困难的要问老师。
三、自学检测:
1.教材P66练习第4 题:
2.教材P66练习第5题:
(1) (2)
3.教材P67习题8.3 3.计算:
(1) (2)
(3) (4)
四、课堂检测:
1. 教材P67习题8.3 4.先化简,再求值:
2. 教材P67习题8.3 5.解方程:
(1) (2)
3. 教材P67习题8.3 6.解不等式:
4.教材P67习题8.3 第7题。
5. 教材P67习题8.3 10.计算:
(1) (2)
自我评价 知识巩固
1.(2004·青海)下列各式中,相等关系一定成立的是( )
A.(x-y)2=(y-x)2 B.(x+6)(x-6)=x2-6
C.(x+y)2=x2+y2 D.6(x-2)+x(2-x)=(x-2)(x-6)
2.(2003·泰州)下列运算正确的是( )
A.x2+x2=2x4 B.a2·a3= a5
C.(-2x2)4=16x6 D.(x+3y)(x-3y)=x2-3y2
3.(2003·河南)下列计算正确的是( )
A.(-4x)·(2x2+3x-1)=-8x3-12x2-4x
B.(x+y)(x2+y2)=x3+y3
C.(-4a-1)(4a-1)=1-16a2
D.(x-2y)2=x2-2xy+4y2
4.(x+2)(x-2)(x2+4)的计算结果是( )
A.x4+16 B.-x4-16 C.x4-16 D.16-x4
5.19922-1991×1993的计算结果是( )
A.1 B.-1 C.2 D.-2
6.对于任意的整数n,能整除代数式(n+3)(n-3)-(n+2)(n-2)的整数是( )
A.4 B.3 C.5 D.2
7.( )(5a+1)=1-25a2,(2x-3) =4x2-9,(-2a2-5b)( )=4a4-25b2
8.99×101=( )( )= .
9.(x-y+z)(-x+y+z)=[z+( )][ ]=z2-( )2.
10.多项式x2+kx+25是另一个多项式的平方,则k= .
11.(a+b)2=(a-b)2+ ,a2+b2=[(a+b)2+(a-b)2]( ),
a2+b2=(a+b)2+ ,a2+b2=(a-b)2+ .
12.计算.
(1)(a+b)2-(a-b)2; (2)(3x-4y)2-(3x+y)2;
(3)(2x+3y)2-(4x-9y)(4x+9y)+(2x-3y)2;
(4)1.23452+0.76552+2.469×0.7655;
(5)(x+2y)(x-y)-(x+y)2.
13.已知m2+n2-6m+10n+34=0,求m+n的值
14.已知a+=4,求a2+和a4+的值.
15.已知(t+58)2=654481,求(t+84)(t+68)的值.
16.解不等式(1-3x)2+(2x-1)2>13(x-1)(x+1).
17.已知a=1990x+1989,b=1990x+1990,c=1990x+1991,求a2+b2+c2-ab-ac-bc的值.
18.(2003·郑州)如果(2a+2b+1)(2a+2b-1)=63,求a+b的值.
19.已知(a+b)2=60,(a-b)2=80,求a2+b2及ab的值.
20.化简(x+y)+(2x+)+(3x+)+…+(9x+),并求当x=2,y=9时的值.
21.若f(x)=2x-1(如f(-2)=2×(-2)-1,f(3)=2×3-1),求的值.
22.观察下面各式:
12+(1×2)2+22=(1×2+1)2
22+(2×3)2+32=(2×3+1)2
32+(3×4)2+42=(3×4+1)2
……
(1)写出第2005个式子;
(2)写出第n个式子,并说明你的结论.
班级: 姓名:
班级: 姓名:
班级: 姓名:
第 6 页 共 6 页
