湖南省株洲市渌江中学2023—2024学年九年级下学期入学考试测数学试题(无答案)
文档属性
| 名称 | 湖南省株洲市渌江中学2023—2024学年九年级下学期入学考试测数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 222.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-23 19:21:40 | ||
图片预览


文档简介
湖南省株洲市渌江中学2024年上学期九年级数学入学考试测试题
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题)
1.sin30°的值为( )
A. B. C. D.
2.用配方法解一元二次方程x2﹣6x+3=0时可配方得( )
A.(x+3)2=6 B.(x﹣3)2=6 C.(x+3)2=3 D.(x﹣3)2=3
3.若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A.1:2 B.2:1 C.1:4 D.4:1
4.在Rt△ABC中,∠C=90°,若AB=5,cosB=,则AC等于( )
A. B.3 C.4 D.5
5.若关于x的一元二次方程mx2﹣2x+1=0有实数根,则实数m的取值范围是( )
A.m≥1 B.m≤1 C.m≥1且m≠0 D.m≤1且m≠0
6.如图,直线a∥b∥c,它们依次交直线m、n于点A、B、C和D、E、F,已知AB=3,BC=6,DE=2,那么EF等于( )
A.2 B.3 C.4 D.5
第6题 第8题 第9题 第10题
7.某地区居民2018年年人均收入为200美元,预计2020年年人均收入将达到1000美元,设2018年到2020年该地区居民人均收入平均年增长率为x,可列方程为( )
A.200(1+2x)=1000 B.200(1+x)2=1000
C.200(1+x2)=1000 D.200+2x=1000
8.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA′:OA=3:5,四边形A′B′C′D′的面积为9cm2,则四边形ABCD的面积为( )
A.15cm2 B.25cm2 C.18cm2 D.27cm2
9.河堤横断面如图所示,堤高BC=4米,迎水坡AB的坡比是1:,则AC的长是( )
A.4米 B.8米 C.10米 D.8米
10.如图是抛物线y=ax2+bx+c的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论中,其中正确的结论的个数是( )
①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不等实数根.
A.1 B.2 C.3 D.4
二.填空题(共8小题)
11.如果x:y=1:2,那么= .
12.二次函数y=x2﹣2x+4的最小值为 .
13.已知二次函数y=﹣2(x﹣2)2+3的顶点坐标是 .
14.已知方程x2﹣3x+2=0的两根分别是x1,x2,则x1+x2的值是 .
15.已知二次函数y=x2+4x+c的图象与x轴的一个交点为(﹣1,0),则它与x轴的另一个交点的坐标是 .
16.如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若AD:DB=2:3,则△ADE与△ABC的面积比等于 .
第16题 第18题
17.卖鱼的商贩为了估计鱼塘中有多少斤鱼,就用渔网先捞出了20条鱼,总重60斤,并在每条鱼上做了标记,随后仍放入鱼塘,一个小时后,再次捞出了30条鱼,发现其中有3条带有标记.根据此数据,可估计鱼塘中有鱼 斤.
18.已知:如图,菱形OABC在直角坐标系中,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=(x>0)经过D点,交BC的延长线于E点,且OB AC=160,有下列四个结论,其中正确的结论是 .
①双曲线的解析式为y=(x>0);②sin∠COA=;③E点的坐标是(4,8);④AC+OB=12.
三.解答题(共10小题)
19.(1)计算:;(2)解方程:3x2﹣2x﹣1=0.
已知方程x2+(m﹣1)x+m﹣17=0的一个根是4,求m的值及方程的另一个根.
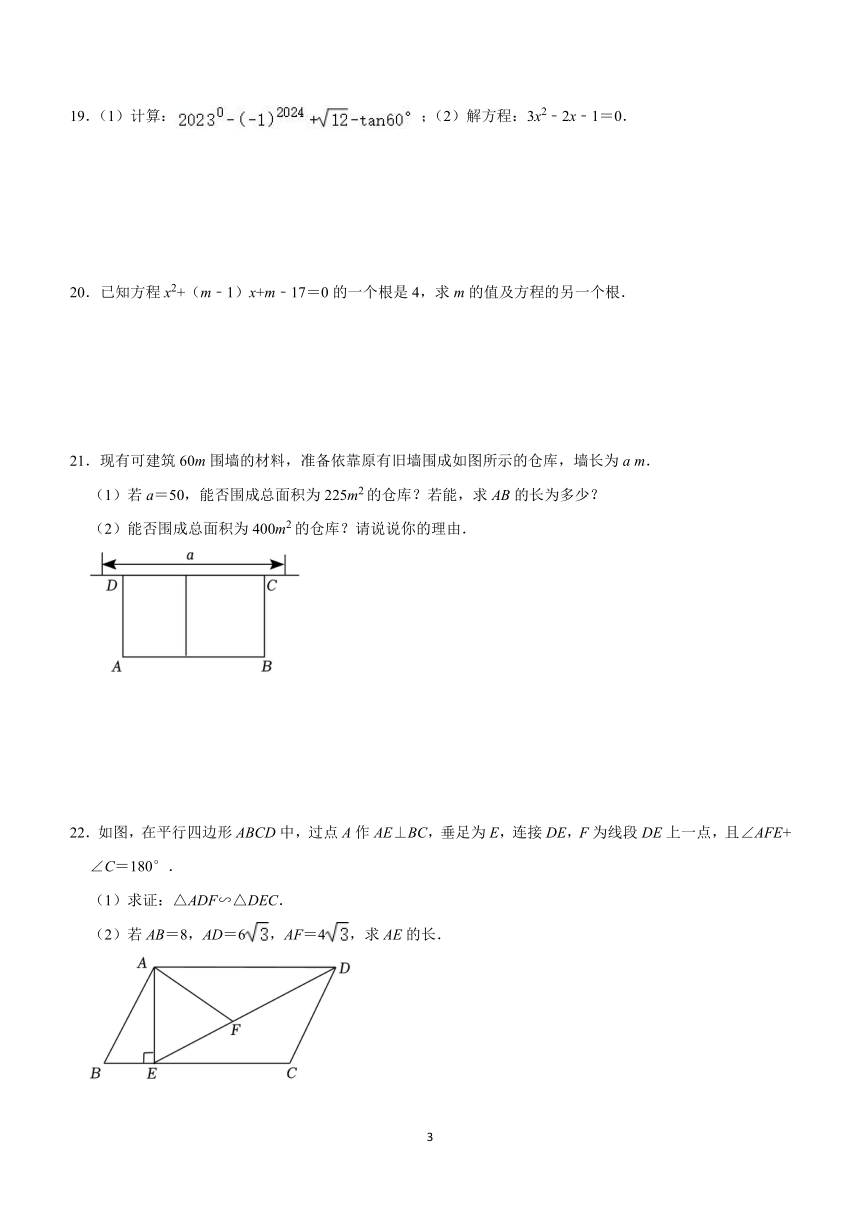
21.现有可建筑60m围墙的材料,准备依靠原有旧墙围成如图所示的仓库,墙长为a m.
(1)若a=50,能否围成总面积为225m2的仓库?若能,求AB的长为多少?
(2)能否围成总面积为400m2的仓库?请说说你的理由.
22.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE+∠C=180°.
(1)求证:△ADF∽△DEC.
(2)若AB=8,AD=6,AF=4,求AE的长.
23.如图,△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E,BC=48,AD=16.
(1)若PN=18,求DE的长;
(2)若矩形PQMN的周长为80,求矩形PQMN的面积.
24.2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某商店以每件35元的价格购进某款亚运会吉祥物,以每件58元的价格出售.经统计,4月份的销售量为256件,6月份的销售量为400件.
(1)求该款吉祥物4月份到6月份销售量的月平均增长率;
(2)从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,月销售量就会增加20件.当该吉祥物售价为多少元时,月销售利润达8400元?
25.已知关于x的方程x2﹣3ax﹣3a﹣6=0,
(1)求证:方程恒有两不等实根;
(2)若x1,x2是该方程的两个实数根,且(x1﹣1)(x2﹣1)=1,求a的值.
26.一艘轮船在某海域上由西向东匀速航行,在A处测得小岛P在北偏东75°方向上,继续向东航行12海里到达B处后,在B处测得小岛P在北偏东60°方向上.
(1)求轮船在B处时与小岛P的距离.
(2)已知在小岛P周围7海里内有暗礁,若轮船继续向东航行,是否有触礁的危险?请说明理由.
27.如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4,cos∠ACH=,点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求的值.
28.如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接AC、BC.
(1)求线段AC的长;
(2)若点P为该抛物线对称轴上的一个动点,当PA=PC时,求点P的坐标;
(3)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题)
1.sin30°的值为( )
A. B. C. D.
2.用配方法解一元二次方程x2﹣6x+3=0时可配方得( )
A.(x+3)2=6 B.(x﹣3)2=6 C.(x+3)2=3 D.(x﹣3)2=3
3.若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A.1:2 B.2:1 C.1:4 D.4:1
4.在Rt△ABC中,∠C=90°,若AB=5,cosB=,则AC等于( )
A. B.3 C.4 D.5
5.若关于x的一元二次方程mx2﹣2x+1=0有实数根,则实数m的取值范围是( )
A.m≥1 B.m≤1 C.m≥1且m≠0 D.m≤1且m≠0
6.如图,直线a∥b∥c,它们依次交直线m、n于点A、B、C和D、E、F,已知AB=3,BC=6,DE=2,那么EF等于( )
A.2 B.3 C.4 D.5
第6题 第8题 第9题 第10题
7.某地区居民2018年年人均收入为200美元,预计2020年年人均收入将达到1000美元,设2018年到2020年该地区居民人均收入平均年增长率为x,可列方程为( )
A.200(1+2x)=1000 B.200(1+x)2=1000
C.200(1+x2)=1000 D.200+2x=1000
8.如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA′:OA=3:5,四边形A′B′C′D′的面积为9cm2,则四边形ABCD的面积为( )
A.15cm2 B.25cm2 C.18cm2 D.27cm2
9.河堤横断面如图所示,堤高BC=4米,迎水坡AB的坡比是1:,则AC的长是( )
A.4米 B.8米 C.10米 D.8米
10.如图是抛物线y=ax2+bx+c的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论中,其中正确的结论的个数是( )
①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不等实数根.
A.1 B.2 C.3 D.4
二.填空题(共8小题)
11.如果x:y=1:2,那么= .
12.二次函数y=x2﹣2x+4的最小值为 .
13.已知二次函数y=﹣2(x﹣2)2+3的顶点坐标是 .
14.已知方程x2﹣3x+2=0的两根分别是x1,x2,则x1+x2的值是 .
15.已知二次函数y=x2+4x+c的图象与x轴的一个交点为(﹣1,0),则它与x轴的另一个交点的坐标是 .
16.如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若AD:DB=2:3,则△ADE与△ABC的面积比等于 .
第16题 第18题
17.卖鱼的商贩为了估计鱼塘中有多少斤鱼,就用渔网先捞出了20条鱼,总重60斤,并在每条鱼上做了标记,随后仍放入鱼塘,一个小时后,再次捞出了30条鱼,发现其中有3条带有标记.根据此数据,可估计鱼塘中有鱼 斤.
18.已知:如图,菱形OABC在直角坐标系中,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=(x>0)经过D点,交BC的延长线于E点,且OB AC=160,有下列四个结论,其中正确的结论是 .
①双曲线的解析式为y=(x>0);②sin∠COA=;③E点的坐标是(4,8);④AC+OB=12.
三.解答题(共10小题)
19.(1)计算:;(2)解方程:3x2﹣2x﹣1=0.
已知方程x2+(m﹣1)x+m﹣17=0的一个根是4,求m的值及方程的另一个根.
21.现有可建筑60m围墙的材料,准备依靠原有旧墙围成如图所示的仓库,墙长为a m.
(1)若a=50,能否围成总面积为225m2的仓库?若能,求AB的长为多少?
(2)能否围成总面积为400m2的仓库?请说说你的理由.
22.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE+∠C=180°.
(1)求证:△ADF∽△DEC.
(2)若AB=8,AD=6,AF=4,求AE的长.
23.如图,△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E,BC=48,AD=16.
(1)若PN=18,求DE的长;
(2)若矩形PQMN的周长为80,求矩形PQMN的面积.
24.2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某商店以每件35元的价格购进某款亚运会吉祥物,以每件58元的价格出售.经统计,4月份的销售量为256件,6月份的销售量为400件.
(1)求该款吉祥物4月份到6月份销售量的月平均增长率;
(2)从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,月销售量就会增加20件.当该吉祥物售价为多少元时,月销售利润达8400元?
25.已知关于x的方程x2﹣3ax﹣3a﹣6=0,
(1)求证:方程恒有两不等实根;
(2)若x1,x2是该方程的两个实数根,且(x1﹣1)(x2﹣1)=1,求a的值.
26.一艘轮船在某海域上由西向东匀速航行,在A处测得小岛P在北偏东75°方向上,继续向东航行12海里到达B处后,在B处测得小岛P在北偏东60°方向上.
(1)求轮船在B处时与小岛P的距离.
(2)已知在小岛P周围7海里内有暗礁,若轮船继续向东航行,是否有触礁的危险?请说明理由.
27.如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4,cos∠ACH=,点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求的值.
28.如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接AC、BC.
(1)求线段AC的长;
(2)若点P为该抛物线对称轴上的一个动点,当PA=PC时,求点P的坐标;
(3)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.
同课章节目录
