第十章 三角形的有关证明 1 全等三角形 第1课时 利用“SAS”“ASA”判定三角形全等(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明 1 全等三角形 第1课时 利用“SAS”“ASA”判定三角形全等(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 21:10:09 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
1 全等三角形
第1课时 利用“SAS”“ASA”判定三角形全等
基 础 练
知识点一 利用“SAS”判定三角形全等
1.如图,点 B,E,C,F在同一条直线上,∥要用SAS证明可以添加的条件是( )
∥
第1题图 第 2 题图
2.如图,公园里有一座假山,要测量假山两端 A,B的距离,先在平地上取一个可以直接到达 A,B的点C,分别延长AC,BC,到 D,E,使连接DE,这样就可以利用三角形全等,通过测量DE 的长得到假山两端A,B的距离,则这两个三角形全等的依据是___________.
3.如图,OA=OB,OC平分求证:
知识点二 利用“ASA”判定三角形全等
4.如图,在△DEC和△BFA 中,点 A,E,F,C在同一直线上,已知 AB∥CD,且 AB=CD,若利用“ASA”证明△DEC≌△BFA,则需要添加的条件是 ( )
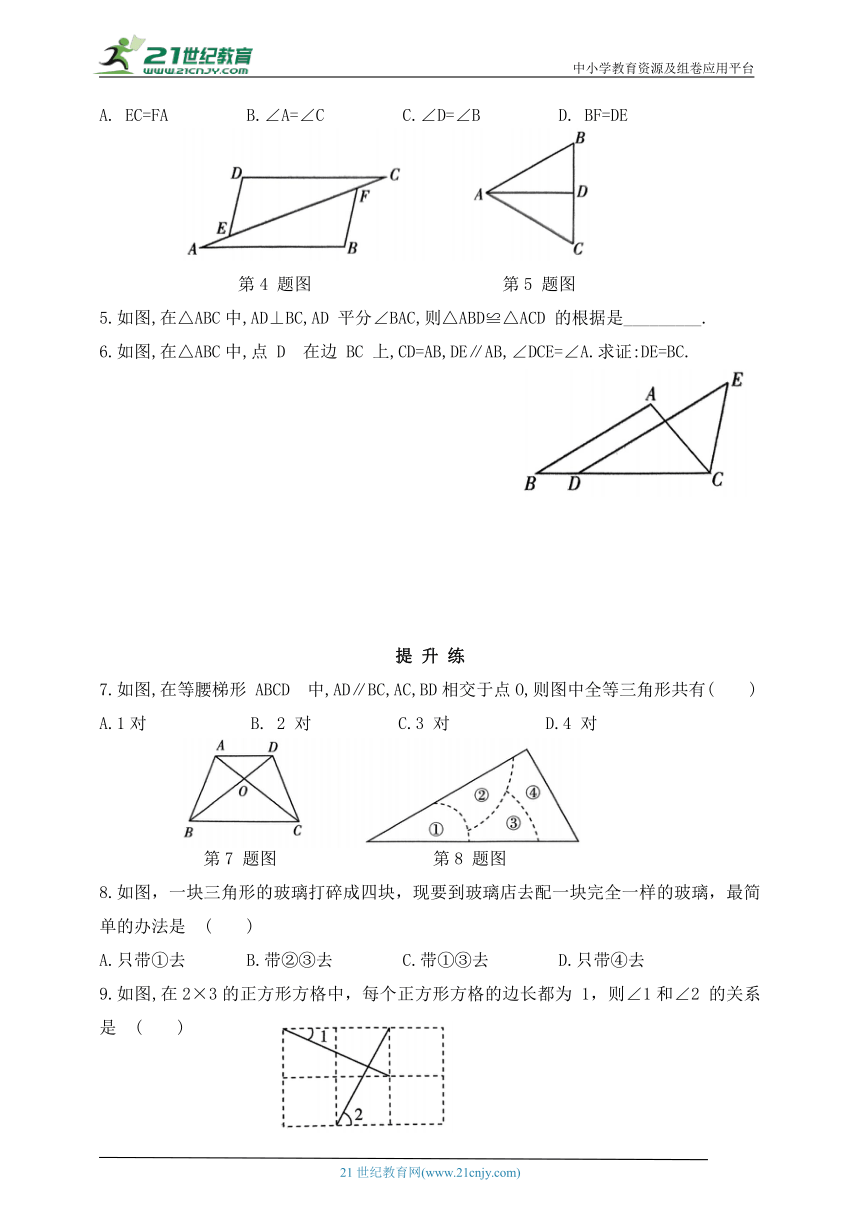
A. EC=FA B.∠A=∠C C.∠D=∠B D. BF=DE
第4 题图 第5 题图
5.如图,在△ABC中,AD⊥BC,AD 平分∠BAC,则△ABD≌△ACD 的根据是_________.
6.如图,在△ABC中,点 D 在边 BC 上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.
提 升 练
7.如图,在等腰梯形 ABCD 中,AD∥BC,AC,BD相交于点O,则图中全等三角形共有( )
A.1对 B. 2 对 C.3 对 D.4 对
第7 题图 第8 题图
8.如图,一块三角形的玻璃打碎成四块,现要到玻璃店去配一块完全一样的玻璃,最简单的办法是 ( )
A.只带①去 B.带②③去 C.带①③去 D.只带④去
9.如图,在2×3的正方形方格中,每个正方形方格的边长都为 1,则∠1和∠2 的关系是 ( )
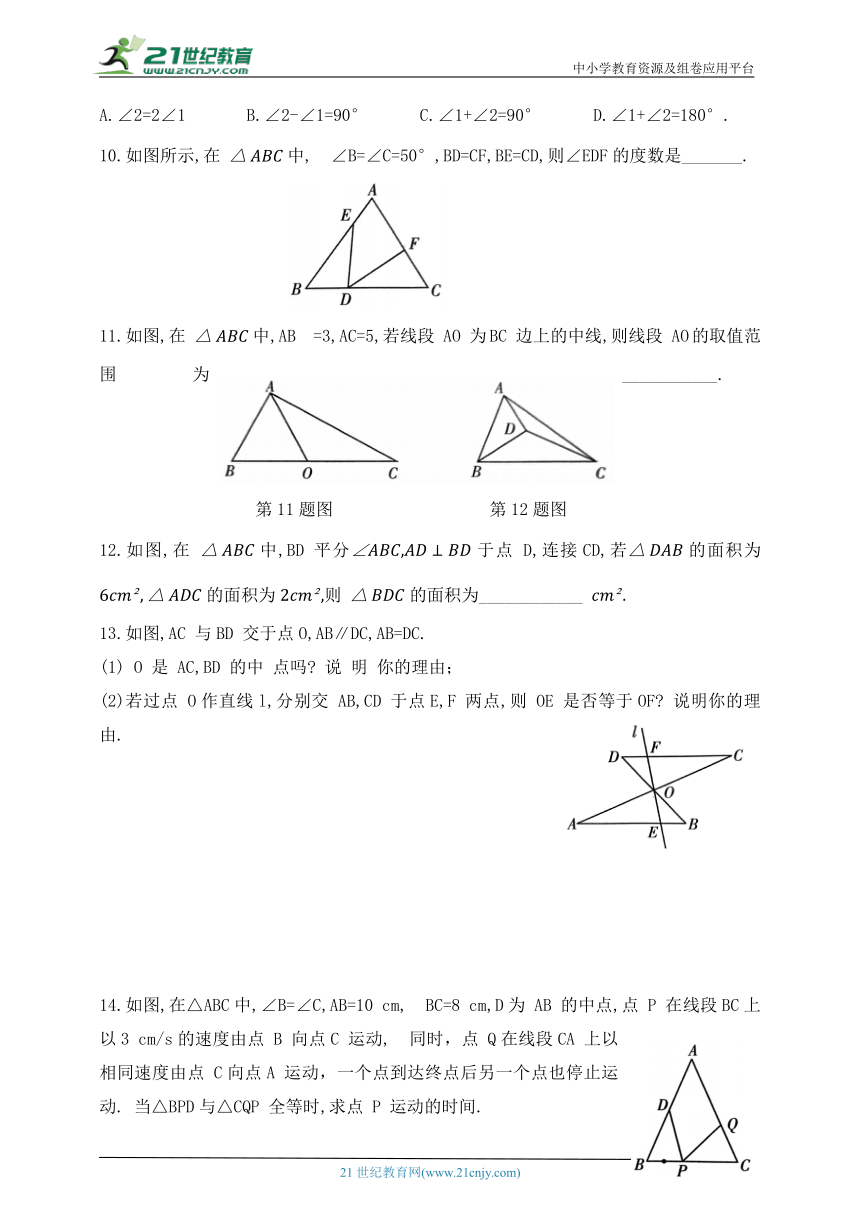
A.∠2=2∠1 B.∠2-∠1=90° C.∠1+∠2=90° D.∠1+∠2=180°.
10.如图所示,在 中, ∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是_______.
11.如图,在 中,AB =3,AC=5,若线段 AO 为BC 边上的中线,则线段 AO的取值范围为___________.
第11题图 第12题图
12.如图,在 中,BD 平分于点 D,连接CD,若的面积为 的面积为则 的面积为____________
13.如图,AC 与BD 交于点O,AB∥DC,AB=DC.
(1) O 是 AC,BD 的中 点吗 说 明 你的理由;
(2)若过点 O作直线l,分别交 AB,CD 于点E,F 两点,则 OE 是否等于OF 说明你的理由.
14.如图,在△ABC中,∠B=∠C,AB=10 cm, BC=8 cm,D为 AB 的中点,点 P 在线段BC上以3 cm/s的速度由点 B 向点C 运动, 同时,点 Q在线段CA 上以相同速度由点 C向点A 运动,一个点到达终点后另一个点也停止运动. 当△BPD与△CQP 全等时,求点 P 运动的时间.
参考答案
1. C 2. SAS
3.证明:∵OC 平分∠AOB,∴∠AOC=∠BOC.
在△AOC 和△BOC中,∴△AOC≌△BOC(SAS)
4. C 5. ASA
6.证明:因为 DE∥AB,所以∠EDC=∠B.
在△CDE和△ABC中. 所以△CDE≌△ABC(ASA),
所以DE=BC.
7. C 8. D 9. C 10.50° 11. 12.8
13.解:(1)点 O 是 AC,BD的中点.
理由:∵AB∥DC,∴∠A=∠C,∠B=∠D.
在△AOB和△COD中, ∴△AOB≌△COD,
∴OA=OC,OB=OD,即点O是AC,BD的中点.
(2)OE=OF.
理由:在△AOE 和△COF中, ∴△AOE≌△COF,
∴OE=OF.
14.解:∵D为AB的中点,
设点 P 运动的时间是 x s,则
若 BD 与CQ 是对应边,则解得
此时 故舍去;
若 BD 与 CP 是对应边,则 解得 符合题意.
综上,点 P 运动的时间是 1 s.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
1 全等三角形
第1课时 利用“SAS”“ASA”判定三角形全等
基 础 练
知识点一 利用“SAS”判定三角形全等
1.如图,点 B,E,C,F在同一条直线上,∥要用SAS证明可以添加的条件是( )
∥
第1题图 第 2 题图
2.如图,公园里有一座假山,要测量假山两端 A,B的距离,先在平地上取一个可以直接到达 A,B的点C,分别延长AC,BC,到 D,E,使连接DE,这样就可以利用三角形全等,通过测量DE 的长得到假山两端A,B的距离,则这两个三角形全等的依据是___________.
3.如图,OA=OB,OC平分求证:
知识点二 利用“ASA”判定三角形全等
4.如图,在△DEC和△BFA 中,点 A,E,F,C在同一直线上,已知 AB∥CD,且 AB=CD,若利用“ASA”证明△DEC≌△BFA,则需要添加的条件是 ( )
A. EC=FA B.∠A=∠C C.∠D=∠B D. BF=DE
第4 题图 第5 题图
5.如图,在△ABC中,AD⊥BC,AD 平分∠BAC,则△ABD≌△ACD 的根据是_________.
6.如图,在△ABC中,点 D 在边 BC 上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.
提 升 练
7.如图,在等腰梯形 ABCD 中,AD∥BC,AC,BD相交于点O,则图中全等三角形共有( )
A.1对 B. 2 对 C.3 对 D.4 对
第7 题图 第8 题图
8.如图,一块三角形的玻璃打碎成四块,现要到玻璃店去配一块完全一样的玻璃,最简单的办法是 ( )
A.只带①去 B.带②③去 C.带①③去 D.只带④去
9.如图,在2×3的正方形方格中,每个正方形方格的边长都为 1,则∠1和∠2 的关系是 ( )
A.∠2=2∠1 B.∠2-∠1=90° C.∠1+∠2=90° D.∠1+∠2=180°.
10.如图所示,在 中, ∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是_______.
11.如图,在 中,AB =3,AC=5,若线段 AO 为BC 边上的中线,则线段 AO的取值范围为___________.
第11题图 第12题图
12.如图,在 中,BD 平分于点 D,连接CD,若的面积为 的面积为则 的面积为____________
13.如图,AC 与BD 交于点O,AB∥DC,AB=DC.
(1) O 是 AC,BD 的中 点吗 说 明 你的理由;
(2)若过点 O作直线l,分别交 AB,CD 于点E,F 两点,则 OE 是否等于OF 说明你的理由.
14.如图,在△ABC中,∠B=∠C,AB=10 cm, BC=8 cm,D为 AB 的中点,点 P 在线段BC上以3 cm/s的速度由点 B 向点C 运动, 同时,点 Q在线段CA 上以相同速度由点 C向点A 运动,一个点到达终点后另一个点也停止运动. 当△BPD与△CQP 全等时,求点 P 运动的时间.
参考答案
1. C 2. SAS
3.证明:∵OC 平分∠AOB,∴∠AOC=∠BOC.
在△AOC 和△BOC中,∴△AOC≌△BOC(SAS)
4. C 5. ASA
6.证明:因为 DE∥AB,所以∠EDC=∠B.
在△CDE和△ABC中. 所以△CDE≌△ABC(ASA),
所以DE=BC.
7. C 8. D 9. C 10.50° 11. 12.8
13.解:(1)点 O 是 AC,BD的中点.
理由:∵AB∥DC,∴∠A=∠C,∠B=∠D.
在△AOB和△COD中, ∴△AOB≌△COD,
∴OA=OC,OB=OD,即点O是AC,BD的中点.
(2)OE=OF.
理由:在△AOE 和△COF中, ∴△AOE≌△COF,
∴OE=OF.
14.解:∵D为AB的中点,
设点 P 运动的时间是 x s,则
若 BD 与CQ 是对应边,则解得
此时 故舍去;
若 BD 与 CP 是对应边,则 解得 符合题意.
综上,点 P 运动的时间是 1 s.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
