7.3.3 函数y=Asin(ωx+φ) 课件(共81张PPT) 2023-2024学年高中数学苏教版必修第一册
文档属性
| 名称 | 7.3.3 函数y=Asin(ωx+φ) 课件(共81张PPT) 2023-2024学年高中数学苏教版必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 17:48:38 | ||
图片预览









文档简介
(共81张PPT)
高中数学苏教版必修第一册
第7章 三角函数
7.3 三角函数的图像和性质
7.3.3 函数y=Asin(ωx+φ)
第1课时 函数y=Asin(ωx+φ)的图象
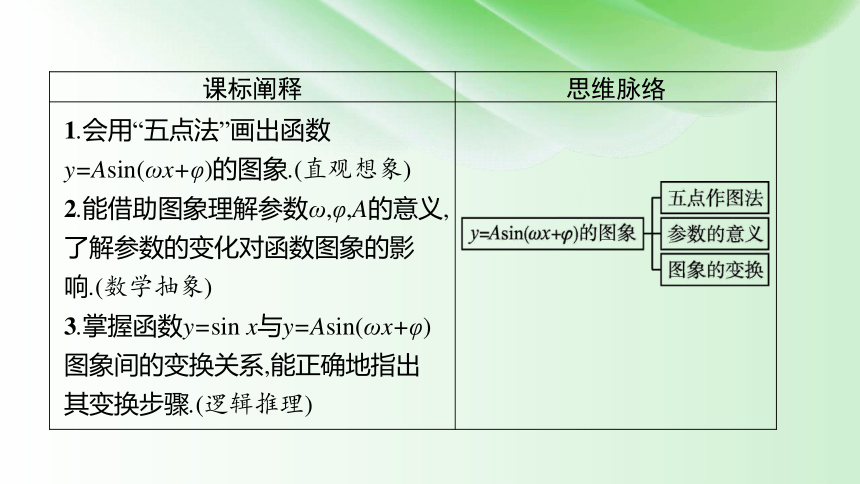
课标阐释 思维脉络
1.会用“五点法”画出函数y=Asin(ωx+φ)的图象.(直观想象)
2.能借助图象理解参数ω,φ,A的意义,了解参数的变化对函数图象的影响.(数学抽象)
3.掌握函数y=sin x与y=Asin(ωx+φ)图象间的变换关系,能正确地指出其变换步骤.(逻辑推理)
情境导入
在物理上,简谐运动中单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y=Asin(ωx+φ)的函数.如图(1)所示是某次实验测得的交流电的电流y随时间x变化的图象.
将测得的图象放大如图(2)所示,可以看出它和正弦曲线很相似,那么函数y=Asin(ωx+φ)与函数y=sin x有什么关系呢
知识点拨
参数φ,ω,A对函数y=Asin(ωx+φ)图象的影响
1.φ对函数y=sin(x+φ)的图象的影响
一般地,函数y=sin(x+φ)的图象可以看作是将函数y=sin x的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位长度而得到的.
2.ω(ω>0且ω≠1)对函数y=sin ωx的图象的影响
函数y=sin ωx(ω>0且ω≠1)的图象,可以看作是将函数y=sin x的图象上所有点的横坐标变为原来的 倍(纵坐标不变)而得到的.
3.A(A>0且A≠1)对函数y=Asin x的图象的影响
函数y=Asin x(A>0且A≠1)的图象,可以看作是将函数y=sin x的图象上所有点的纵坐标变为原来的A倍(横坐标不变)而得到的.
4.函数y=sin(ωx+φ)(ω>0,φ≠0)的图象,可以看作是将函数y=sin ωx的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移 个单位长度而得到的.
名师点析 φ,ω,A对函数y=Asin(ωx+φ)的图象的影响
(1)φ>0时,函数图象向左平移,φ<0时,函数图象向右平移,即“加左减右”.
(2)|ω|越大,函数图象的周期越小,|ω|越小,周期越大,周期与|ω|为反比例关系.
(3)A越大,函数图象的最大值越大,最大值与A是正比例关系.
微判断
(1)把函数y=sin x的图象向右平移2个单位长度得到函数y=sin(x+2)的图象.( )
(2)把函数y=sin x的图象向左平移2π个单位长度后得到的图象与原图象重合.( )
答案 (1)× (2)√ (3)× (4)×
微练习 1
为了得到y=sin 4x,x∈R的图象,只需把正弦曲线上所有点的( )
A.横坐标变为原来的4倍,纵坐标不变
B.横坐标变为原来的 倍,纵坐标不变
C.纵坐标变为原来的4倍,横坐标不变
D.纵坐标变为原来的 倍,横坐标不变
答案 B
解析 ω=4>1,因此只需把正弦曲线上所有点的横坐标变为原来的 倍,纵坐标不变.
微练习 2
把函数y=2sin 3x的图象上所有点的横坐标变为原来的2倍,纵坐标变为原来的3倍,得到 的图象.
探究一
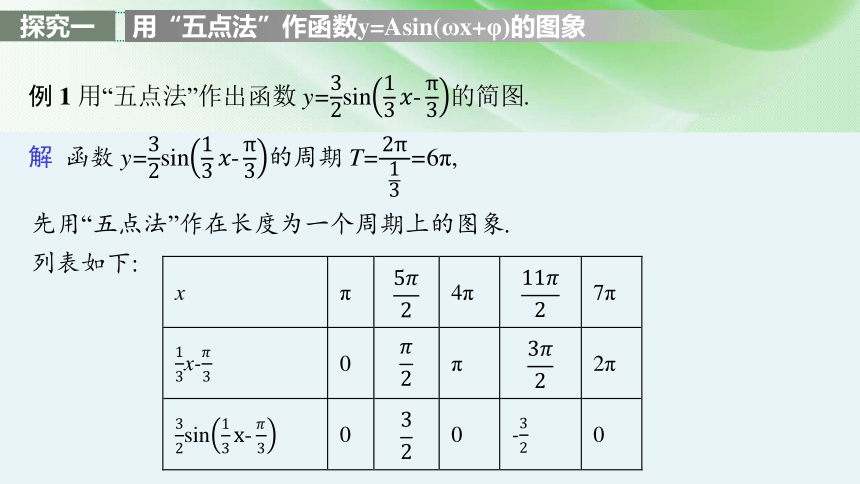
用“五点法”作函数y=Asin(ωx+φ)的图象
先用“五点法”作在长度为一个周期上的图象.
列表如下:
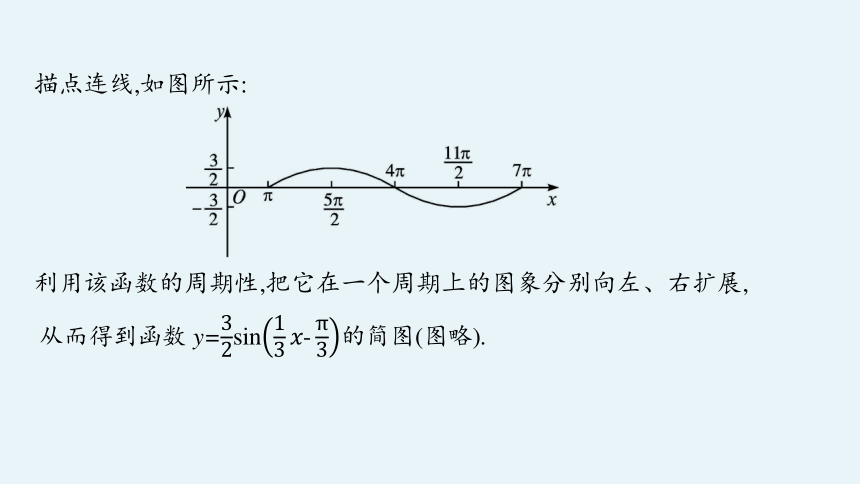
描点连线,如图所示:
利用该函数的周期性,把它在一个周期上的图象分别向左、右扩展,
反思感悟“五点法”作函数y=Asin(ωx+φ)(x∈R)的图象的步骤
(2)描点.
(3)连线得函数在一个周期内的图象.
(4)左右平移得到y=Asin(ωx+φ),x∈R的图象.
解 列表如下:
探究二
函数图象的平移变换
答案 B
反思感悟平移变换的策略
(1)先确定平移方向和平移的量.
(2)当x的系数是1时,若φ>0,则左移φ个单位长度;若φ<0,则右移|φ|个单位长度.
答案 C
探究三
函数图象的伸缩变换
答案 C
素养形成
函数图象变换中的一题多解
典例1由函数y=sin x的图象经过怎样的变换,可以得到函数y=-2sin(2x- )+1的图象.
思路点拨本题考查三角函数的图象变换问题,可以从先“平移变换”或先“伸缩变换”两种不同变换顺序的角度去考虑,得到答案.
名师点析 在方法1中,先伸缩,后平移;在方法2中,先平移,后伸缩.两种变换方法中平移的单位长度是不同的(分别为 ),但得到的结果都是一致的.
答案 B
当堂检测
答案 A
解析 两个相邻点的距离为半个周期π.
答案 D
3.将函数y=sin 图象上各点的纵坐标不变,横坐标变为原来的5倍,可得到函数 的图象.
4.已知函数f(x)的图象上每一点的纵坐标保持不变,横坐标变为原来的2倍,然后把所得的图象沿x轴向左平移 个单位长度,这样得到的图象与
y= sin x的图象相同,求f(x)的解析式.
解 ①先用“五点法”作出一个周期的图象,列表:
高中数学苏教版必修第一册
第7章 三角函数
7.3 三角函数的图像和性质
7.3.3 函数y=Asin(ωx+φ)
第2课时 函数y=Asin(ωx+φ)的性质及应用
课标阐释 思维脉络
1.能根据y=Asin(ωx+φ)的部分图象,确定其解析式.(直观想象)
2.了解函数y=Asin(ωx+φ)的图象的物理意义,能指出简谐运动中的振幅、周期、相位、初相.(数学抽象)
3.会根据三角函数的图象与性质讨论函数y=Asin(ωx+φ)的性质.(逻辑推理)
情境导入
在物理和工程技术的许多问题中,经常会遇到形如y=Asin(ωx+φ) 的函数(其中A,ω,φ为常数),例如,在简谐运动中位移与时间的函数关系就是形如y=Asin(ωx+φ)的函数,其中振子在一段时间内的图象如图所示.
(1)你能根据图象求出A,ω,φ吗
(2)根据图象你能写出函数y=Asin(ωx+φ)的单调区间吗
(3)图象对应函数的对称中心坐标和对称轴方程分别是什么
知识点拨
函数y=Asin(ωx+φ)(A>0,ω>0)的有关性质
名师点析 根据零点求函数y=Asin(ωx+φ)的解析式要注意:
从寻找“五点法”中的第一零点 (也叫初始点)作为突破口,以y=Asin(ωx+φ)(A>0,ω>0)为例,位于增区间上离y轴最近的那个零点最适合作为“五点”中的第一个点.
微判断
(1)y=Asin(ωx+φ)的图象既是中心对称图形,又是轴对称图形.( )
(2)在y=Asin(ωx+φ)的图象中,相邻的两条对称轴的距离为1个周期.( )
答案 (1)√ (2)× (3)× (4)√
微练习
已知函数f(x)=2sin(ωx+φ)的图象如图所示,则f 等于( )
A. B.0
C.2 D.-2
答案 B
探究一
三角函数图象变换的应用
答案 B
反思感悟函数y=Asin(ωx+φ)的奇偶性:
(1)当φ=kπ(k∈Z)时,函数是奇函数;
(2)当φ=kπ+ (k∈Z)时,函数是偶函数;
(3)当φ≠kπ,且φ≠kπ+ (k∈Z)时,函数是非奇非偶函数.
探究二
由图象确定函数解析式
反思感悟给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法.
(1)逐一定参法:先通过图象确定A和ω,再选取“第一零点”(即“五点法”作图中的第一个点)的数据代入“ωx+φ=0”(要注意正确判断哪一点是“第一零点”),求得φ的值.
(2)待定系数法:通过若干特殊点代入函数式,可以求得相关待定系数A,ω,φ.但需要注意的是,要认清所选择的点属于五个点中的哪一点,并能正确代入解析式.
(3)图象变换法:运用逆向思维的方法,先确定函数的基本解析式y=Asin ωx,再根据图象平移规律确定相关的参数.
变式训练1某函数部分图象如图所示,它的函数的解析式可能是( )
答案 C
探究三
函数y=Asin(ωx+φ)性质的综合应用
反思感悟研究函数y=Asin(ωx+φ)性质的基本策略:
(1)首先将所给函数的解析式转化为y=Asin(ωx+φ)的形式;
(2)熟记正弦函数y=sin x的图象与基本性质;
(3)充分利用整体代换思想解决问题;
(4)熟记有关函数y=Asin(ωx+φ)的奇偶性、对称性、单调性的重要结论.
素养形成
一道确定函数解析式问题的多种解法
典例 如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象,求这个函数的解析式.
反思感悟 确定参数φ的方法
(1)把图象上的一个已知点的坐标代入来求.(2)寻找“五点法”中的某一个点来求,具体如下:利用“第一点”时,令ωx+φ=0;利用“第二点”(即图象的“峰点”)时,令ωx+φ= ;利用“第三点”(即图象下降时与x轴的交点)时,令ωx+φ=π;利用“第四点”(即图象的“谷点”)时,令ωx+φ= ;利用“第五点”时,令ωx+φ=2π.注意:要观察题目所给图象是否适合用“五点法”求解.
当堂检测
1.如图,是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象,则其解析式为( )
答案 B
答案 A
答案 B
答案 2
5.已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π])的部分图象如图所示.若
谢谢观看
高中数学苏教版必修第一册
第7章 三角函数
7.3 三角函数的图像和性质
7.3.3 函数y=Asin(ωx+φ)
第1课时 函数y=Asin(ωx+φ)的图象
课标阐释 思维脉络
1.会用“五点法”画出函数y=Asin(ωx+φ)的图象.(直观想象)
2.能借助图象理解参数ω,φ,A的意义,了解参数的变化对函数图象的影响.(数学抽象)
3.掌握函数y=sin x与y=Asin(ωx+φ)图象间的变换关系,能正确地指出其变换步骤.(逻辑推理)
情境导入
在物理上,简谐运动中单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y=Asin(ωx+φ)的函数.如图(1)所示是某次实验测得的交流电的电流y随时间x变化的图象.
将测得的图象放大如图(2)所示,可以看出它和正弦曲线很相似,那么函数y=Asin(ωx+φ)与函数y=sin x有什么关系呢
知识点拨
参数φ,ω,A对函数y=Asin(ωx+φ)图象的影响
1.φ对函数y=sin(x+φ)的图象的影响
一般地,函数y=sin(x+φ)的图象可以看作是将函数y=sin x的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位长度而得到的.
2.ω(ω>0且ω≠1)对函数y=sin ωx的图象的影响
函数y=sin ωx(ω>0且ω≠1)的图象,可以看作是将函数y=sin x的图象上所有点的横坐标变为原来的 倍(纵坐标不变)而得到的.
3.A(A>0且A≠1)对函数y=Asin x的图象的影响
函数y=Asin x(A>0且A≠1)的图象,可以看作是将函数y=sin x的图象上所有点的纵坐标变为原来的A倍(横坐标不变)而得到的.
4.函数y=sin(ωx+φ)(ω>0,φ≠0)的图象,可以看作是将函数y=sin ωx的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移 个单位长度而得到的.
名师点析 φ,ω,A对函数y=Asin(ωx+φ)的图象的影响
(1)φ>0时,函数图象向左平移,φ<0时,函数图象向右平移,即“加左减右”.
(2)|ω|越大,函数图象的周期越小,|ω|越小,周期越大,周期与|ω|为反比例关系.
(3)A越大,函数图象的最大值越大,最大值与A是正比例关系.
微判断
(1)把函数y=sin x的图象向右平移2个单位长度得到函数y=sin(x+2)的图象.( )
(2)把函数y=sin x的图象向左平移2π个单位长度后得到的图象与原图象重合.( )
答案 (1)× (2)√ (3)× (4)×
微练习 1
为了得到y=sin 4x,x∈R的图象,只需把正弦曲线上所有点的( )
A.横坐标变为原来的4倍,纵坐标不变
B.横坐标变为原来的 倍,纵坐标不变
C.纵坐标变为原来的4倍,横坐标不变
D.纵坐标变为原来的 倍,横坐标不变
答案 B
解析 ω=4>1,因此只需把正弦曲线上所有点的横坐标变为原来的 倍,纵坐标不变.
微练习 2
把函数y=2sin 3x的图象上所有点的横坐标变为原来的2倍,纵坐标变为原来的3倍,得到 的图象.
探究一
用“五点法”作函数y=Asin(ωx+φ)的图象
先用“五点法”作在长度为一个周期上的图象.
列表如下:
描点连线,如图所示:
利用该函数的周期性,把它在一个周期上的图象分别向左、右扩展,
反思感悟“五点法”作函数y=Asin(ωx+φ)(x∈R)的图象的步骤
(2)描点.
(3)连线得函数在一个周期内的图象.
(4)左右平移得到y=Asin(ωx+φ),x∈R的图象.
解 列表如下:
探究二
函数图象的平移变换
答案 B
反思感悟平移变换的策略
(1)先确定平移方向和平移的量.
(2)当x的系数是1时,若φ>0,则左移φ个单位长度;若φ<0,则右移|φ|个单位长度.
答案 C
探究三
函数图象的伸缩变换
答案 C
素养形成
函数图象变换中的一题多解
典例1由函数y=sin x的图象经过怎样的变换,可以得到函数y=-2sin(2x- )+1的图象.
思路点拨本题考查三角函数的图象变换问题,可以从先“平移变换”或先“伸缩变换”两种不同变换顺序的角度去考虑,得到答案.
名师点析 在方法1中,先伸缩,后平移;在方法2中,先平移,后伸缩.两种变换方法中平移的单位长度是不同的(分别为 ),但得到的结果都是一致的.
答案 B
当堂检测
答案 A
解析 两个相邻点的距离为半个周期π.
答案 D
3.将函数y=sin 图象上各点的纵坐标不变,横坐标变为原来的5倍,可得到函数 的图象.
4.已知函数f(x)的图象上每一点的纵坐标保持不变,横坐标变为原来的2倍,然后把所得的图象沿x轴向左平移 个单位长度,这样得到的图象与
y= sin x的图象相同,求f(x)的解析式.
解 ①先用“五点法”作出一个周期的图象,列表:
高中数学苏教版必修第一册
第7章 三角函数
7.3 三角函数的图像和性质
7.3.3 函数y=Asin(ωx+φ)
第2课时 函数y=Asin(ωx+φ)的性质及应用
课标阐释 思维脉络
1.能根据y=Asin(ωx+φ)的部分图象,确定其解析式.(直观想象)
2.了解函数y=Asin(ωx+φ)的图象的物理意义,能指出简谐运动中的振幅、周期、相位、初相.(数学抽象)
3.会根据三角函数的图象与性质讨论函数y=Asin(ωx+φ)的性质.(逻辑推理)
情境导入
在物理和工程技术的许多问题中,经常会遇到形如y=Asin(ωx+φ) 的函数(其中A,ω,φ为常数),例如,在简谐运动中位移与时间的函数关系就是形如y=Asin(ωx+φ)的函数,其中振子在一段时间内的图象如图所示.
(1)你能根据图象求出A,ω,φ吗
(2)根据图象你能写出函数y=Asin(ωx+φ)的单调区间吗
(3)图象对应函数的对称中心坐标和对称轴方程分别是什么
知识点拨
函数y=Asin(ωx+φ)(A>0,ω>0)的有关性质
名师点析 根据零点求函数y=Asin(ωx+φ)的解析式要注意:
从寻找“五点法”中的第一零点 (也叫初始点)作为突破口,以y=Asin(ωx+φ)(A>0,ω>0)为例,位于增区间上离y轴最近的那个零点最适合作为“五点”中的第一个点.
微判断
(1)y=Asin(ωx+φ)的图象既是中心对称图形,又是轴对称图形.( )
(2)在y=Asin(ωx+φ)的图象中,相邻的两条对称轴的距离为1个周期.( )
答案 (1)√ (2)× (3)× (4)√
微练习
已知函数f(x)=2sin(ωx+φ)的图象如图所示,则f 等于( )
A. B.0
C.2 D.-2
答案 B
探究一
三角函数图象变换的应用
答案 B
反思感悟函数y=Asin(ωx+φ)的奇偶性:
(1)当φ=kπ(k∈Z)时,函数是奇函数;
(2)当φ=kπ+ (k∈Z)时,函数是偶函数;
(3)当φ≠kπ,且φ≠kπ+ (k∈Z)时,函数是非奇非偶函数.
探究二
由图象确定函数解析式
反思感悟给出y=Asin(ωx+φ)的图象的一部分,确定A,ω,φ的方法.
(1)逐一定参法:先通过图象确定A和ω,再选取“第一零点”(即“五点法”作图中的第一个点)的数据代入“ωx+φ=0”(要注意正确判断哪一点是“第一零点”),求得φ的值.
(2)待定系数法:通过若干特殊点代入函数式,可以求得相关待定系数A,ω,φ.但需要注意的是,要认清所选择的点属于五个点中的哪一点,并能正确代入解析式.
(3)图象变换法:运用逆向思维的方法,先确定函数的基本解析式y=Asin ωx,再根据图象平移规律确定相关的参数.
变式训练1某函数部分图象如图所示,它的函数的解析式可能是( )
答案 C
探究三
函数y=Asin(ωx+φ)性质的综合应用
反思感悟研究函数y=Asin(ωx+φ)性质的基本策略:
(1)首先将所给函数的解析式转化为y=Asin(ωx+φ)的形式;
(2)熟记正弦函数y=sin x的图象与基本性质;
(3)充分利用整体代换思想解决问题;
(4)熟记有关函数y=Asin(ωx+φ)的奇偶性、对称性、单调性的重要结论.
素养形成
一道确定函数解析式问题的多种解法
典例 如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象,求这个函数的解析式.
反思感悟 确定参数φ的方法
(1)把图象上的一个已知点的坐标代入来求.(2)寻找“五点法”中的某一个点来求,具体如下:利用“第一点”时,令ωx+φ=0;利用“第二点”(即图象的“峰点”)时,令ωx+φ= ;利用“第三点”(即图象下降时与x轴的交点)时,令ωx+φ=π;利用“第四点”(即图象的“谷点”)时,令ωx+φ= ;利用“第五点”时,令ωx+φ=2π.注意:要观察题目所给图象是否适合用“五点法”求解.
当堂检测
1.如图,是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象,则其解析式为( )
答案 B
答案 A
答案 B
答案 2
5.已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π])的部分图象如图所示.若
谢谢观看
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
