5.3 函数的单调性 课件(共69张PPT)2023-2024学年高中数学苏教版必修第一册
文档属性
| 名称 | 5.3 函数的单调性 课件(共69张PPT)2023-2024学年高中数学苏教版必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-26 17:49:48 | ||
图片预览


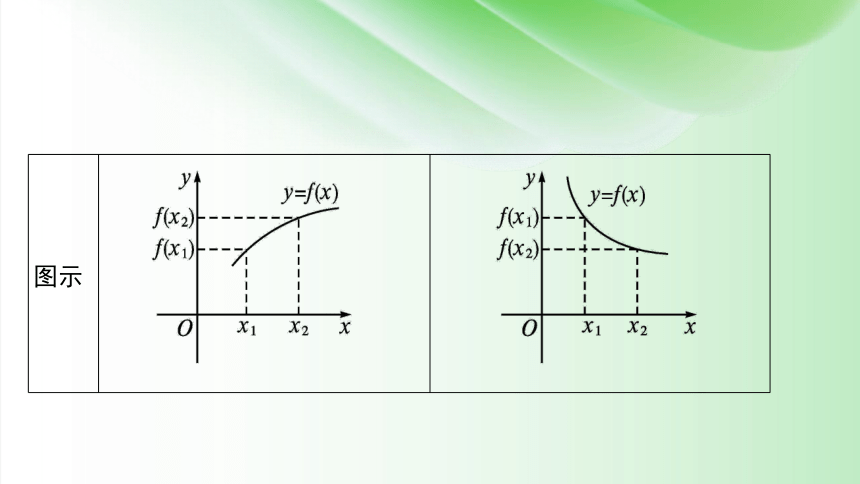






文档简介
(共69张PPT)
高中数学苏教版必修第一册
第5章 函数的概念与性质
5.3 函数的单调性
第1课时 函数的单调性
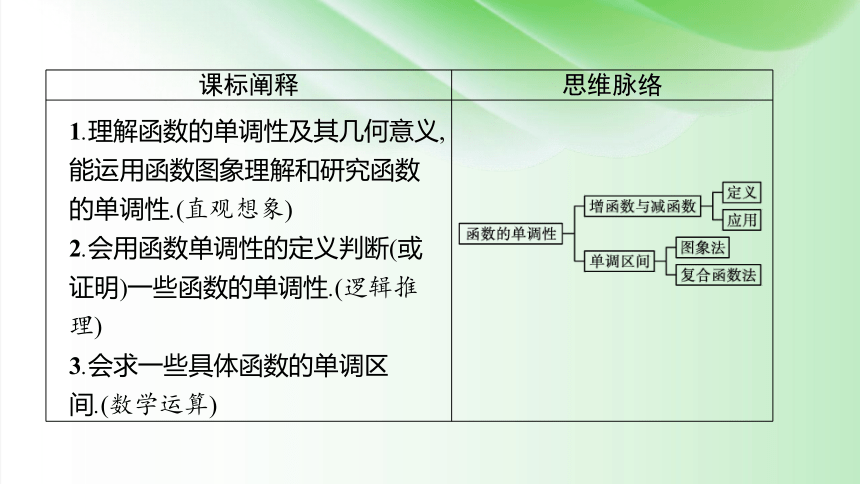
课标阐释 思维脉络
1.理解函数的单调性及其几何意义,能运用函数图象理解和研究函数的单调性.(直观想象)
2.会用函数单调性的定义判断(或证明)一些函数的单调性.(逻辑推理)
3.会求一些具体函数的单调区间.(数学运算)
情境导入
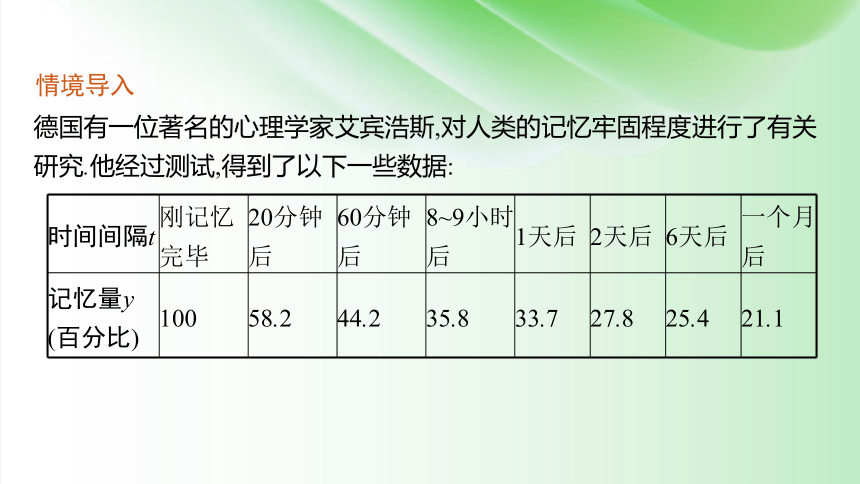
德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:
时间间隔t 刚记忆完毕 20分钟后 60分钟后 8~9小时后 1天后 2天后 6天后 一个月后
记忆量y (百分比) 100 58.2 44.2 35.8 33.7 27.8 25.4 21.1
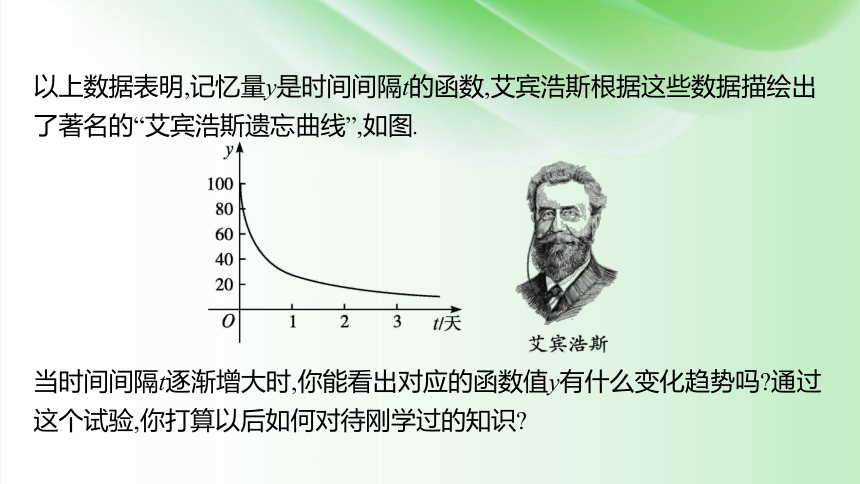
以上数据表明,记忆量y是时间间隔t的函数,艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯遗忘曲线”,如图.
当时间间隔t逐渐增大时,你能看出对应的函数值y有什么变化趋势吗 通过这个试验,你打算以后如何对待刚学过的知识
知识点拨
一、增函数与减函数
条件 设函数y=f(x)的定义域为A,区间I A. 如果对于区间I内的任意两个值x1,x2,当x1f(x2)
结论 那么称y=f(x)在区间I上是增函数,I称为y=f(x)的增区间 那么称y=f(x)在区间I上是减函数,I称为y=f(x)的减区间
图示
名师点析 增(减)函数定义中的x1,x2的特征
(1)任意性,即“任意两个值x1,x2”中“任意”二字绝不能去掉,证明时不能以特殊代替一般;
(2)有大小,通常规定x1(3)属于同一个单调区间.
这三个条件缺一不可.
微练习 1
下列函数在区间(0,+∞)上是减函数的是( )
A.y=- B.y=x
C.y=x2 D.y=1-x
答案 D
解析 函数y=1-x在区间(0,+∞)上是减函数,其余函数在(0,+∞)上均为增函数,故选D.
微练习 2
已知函数f(x)是定义在R上的增函数,则f(x)=0的根( )
A.有且只有一个 B.有两个
C.至多一个 D.以上均不对
答案 D
解析 因为f(x)在R上是增函数,所以对任意x1,x2∈R,若x1二、函数的单调性与单调区间
如果函数y=f(x)在区间I上是增函数或减函数,那么称函数y=f(x)在区间I上具有单调性,增区间和减区间统称为单调区间.
名师点析 1.区间I必为函数定义域A的子集,即I A,所以单调性是函数定义域内的局部性质.
2.函数的单调区间可以是整个定义域,也可以是定义域的真子集.如y=x在整个定义域(-∞,+∞)上是增函数,y=-x在整个定义域(-∞,+∞)上是减函数,但y=x2在定义域(-∞,+∞)上不具有单调性,其在(-∞,0)上是减函数,在(0,+∞)上是增函数.
3.一个函数出现两个或两个以上单调区间时,单调区间用“,”隔开,或者用“和”连接,不能用“并”或“且”连接.
微思考
函数y= 在定义域上是减函数吗
提示 不是.y= 在(-∞,0)上是减函数,在(0,+∞)上也是减函数,但不能说y=在(-∞,0)∪(0,+∞)上是减函数.
微练习
函数y=f(x)的图象如图所示,其减区间是( )
A.[-4,4]
B.[-4,-3]和[1,4]
C.[-3,1]
D.[-3,4]
答案 B
解析 由图可知,函数y=f(x)的减区间为[-4,-3]和[1,4].故选B.
探究一
函数单调性的判断与证明
例1证明函数f(x)=x+ 在(0,1)上是减函数.
证明 设x1,x2是区间(0,1)上的任意两个实数,且x1∵0∴x1x2>0,x1x2-1<0,x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴f(x)=x+ 在(0,1)上是减函数.
反思感悟利用定义证明函数单调性的步骤
(1)取值:设x1,x2是该区间内的任意两个值,且x1(2)作差变形:作差f(x1)-f(x2),并通过因式分解、通分、配方、有理化等手段,转化为易判断正负的式子.
(3)定号:确定f(x1)-f(x2)的符号.
(4)结论:根据f(x1)-f(x2)的符号及定义判断单调性.
变式训练1试用函数单调性的定义证明f(x)= 在(1,+∞)上是减函数.
因为1所以x2-x1>0,x1-1>0,x2-1>0,
所以f(x1)>f(x2),
所以f(x)在(1,+∞)上是减函数.
探究二
求函数的单调区间
例2求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(3)f(x)=-x2+2|x|+3.
解 (1)函数f(x)=- 的单调区间为(-∞,0),(0,+∞),其在(-∞,0),(0,+∞)上都是增函数.
(2)当x≥1时,f(x)是增函数,当x<1时,f(x)是减函数,所以f(x)的单调区间为
(-∞,1),[1,+∞),并且函数f(x)在(-∞,1)上是减函数,在[1,+∞)上是增函数.
根据解析式可作出函数的图象如图所示,由图象可知,函数f(x)的单调区间为(-∞,-1],[-1,0],[0,1],[1,+∞).
f(x)在(-∞,-1],[0,1]上是增函数,在[-1,0],[1,+∞)上是减函数.
反思感悟1.求函数单调区间的方法
(1)利用基本初等函数的单调性,如本例(1)和(2),其中分段函数的单调区间要根据函数的自变量的取值范围分段求解;
(2)利用函数的图象,如本例(3).
2.若所求出函数的增区间或减区间不唯一,函数的单调区间之间要用“,”或“和”连接,如本例(3).
变式训练2(1)根据图象说出函数在每一单调区间上,是增函数还是减函数;
(2)写出y=|x2-2x-3|的单调区间.
解 (1)函数在[-1,0],[2,4]上是减函数,在[0,2],[4,5]上是增函数.
(2)先画出
则y=|x2-2x-3|的减区间为(-∞,-1],[1,3];增区间为[-1,1],[3,+∞).
探究三
函数单调性的综合应用
例3已知函数f(x)=x2+ax+b.
(1)若函数f(x)的图象过点(1,4)和(2,5),求f(x)的解析式;
(2)若函数f(x)在区间[1,2]上不具有单调性,求实数a的取值范围.
解 (1)∵f(x)=x2+ax+b过点(1,4)和(2,5),
(2)由f(x)在区间[1,2]上不具有单调性可知1<- <2,即-4故实数a的取值范围为(-4,-2).
延伸探究把本例(2)条件“不具有单调性”改为“具有单调性”,求实数a的取值范围.
反思感悟函数单调性的应用
(1)函数单调性定义的“双向性”:利用定义可以判断、证明函数的单调性,反过来,若已知函数的单调性可以确定函数中参数的取值范围.
(2)若一个函数在区间[a,b]上具有单调性,则此函数在这一单调区间内的任意子集上也具有单调性.
变式训练3已知函数g(x)在(-∞,+∞)上是增函数,且g(2x-3)>g(5x+6),求实数x的取值范围.
解 ∵g(x)在(-∞,+∞)上是增函数,且g(2x-3)>g(5x+6),
∴2x-3>5x+6,即x<-3.
故实数x的取值范围为(-∞,-3).
素养形成
抽象函数的单调性
抽象函数是指没有给出具体解析式的函数.
判断抽象函数单调性的方法:
1.凑:凑定义或凑已知,利用定义或已知条件得出结论;
2.赋值:给变量赋值要根据条件与结论的关系,有时可能要进行多次尝试.
典例 已知定义在(0,+∞)上的函数f(x)对任意x,y∈(0,+∞),恒有f(xy)=f(x)+f(y),且当00,判断f(x)在(0,+∞)上的单调性并给出理由.
解 f(x)在(0,+∞)上是减函数.
理由如下,设x1,x2是区间(0,+∞)上的任意两个值,且x1∴f(x1)-f(x2)>0,
即f(x1)>f(x2).
∴函数f(x)在(0,+∞)上是减函数.
点评一般地,若给出的抽象函数的性质为“f(x+y)=…”,则称这类抽象函数为“和型抽象函数”,研究“和型抽象函数”的单调性的基本方法是将x拆成两个数的和“(x-y)+y”,利用所给的性质及条件,即可确定其单调性;类似地,“积型抽象函数”(即“f(xy)=…”)只需将x拆成两个数的积“x=y· (y≠0)”即可.
当堂检测
1.如图是定义在区间[-5,5]上的函数y=f(x),则下列关于函数f(x)的说法错误的是( )
A.函数在区间[-5,-3]上是增函数
B.函数在区间[1,4]上是增函数
C.函数在区间[-3,1]∪[4,5]上是减函数
D.函数在区间[-5,5]上没有单调性
答案 C
解析 由图可知,f(x)在区间[-3,1],[4,5]上是减函数,单调区间不可以用并集“∪”连接,故选C.
2.函数f(x)在R上是减函数,则有( )
A.f(3)C.f(3)>f(5) D.f(3)≥f(5)
答案 C
解析 ∵3<5,且f(x)在R上是减函数,∴f(3)>f(5).
3.(2020北京北理工附中期中)下列函数在区间(0,+∞)上为增函数的是( )
答案 B
对于C,函数y=(x-1)2+1在(0,1)上是减函数,在(1,+∞)上是增函数,故C错误;
对于D,函数y=-x2在(0,+∞)上是减函数,故D错误.
故选B.
4.(2020浙江宁波高二期中)已知函数f(x)在R上是减函数,且f(2)=-1,则满足f(2x-4)>-1的实数x的取值范围是 .
答案 (-∞,3)
解析 由f(2)=-1知,若满足f(2x-4)>-1,
则f(2x-4)>f(2).
又函数f(x)在R上是减函数,则2x-4<2,解得x<3,
所以实数x的取值范围为(-∞,3).
5.已知函数f(x)= (k≠0)在区间(0,+∞)上是增函数,则实数k的取值范围是 .
答案 (-∞,0)
解析 结合反比例函数的单调性可知k<0.
高中数学苏教版必修第一册
第5章 函数的概念与性质
5.3 函数的单调性
第2课时 函数的最大(小)值
课标阐释 思维脉络
1.理解函数的最大值和最小值的概念及其几何意义.(数学抽象)
2.能借助函数的图象和单调性,求一些简单函数的最值.(直观想象)
3.能利用函数的最值解决有关的实际应用问题.(数学建模)
情境导入
请同学们认真观察一次函数f(x)=x和二次函数f(x)=x2的图象,在它们的图象上是否存在最高点或最低点 显然,一次函数f(x)=x的图象上不存在最高点,也不存在最低点.二次函数f(x)=x2的图象上不存在最高点,但存在最低点(0,0),即坐标原点.即当一个函数f(x)的图象有最低点时,我们就说函数f(x)有最小值;而一次函数f(x)=x的图象没有最低点,所以函数f(x)=x没有最小值.
你能用数学语言描述函数最小值的定义吗
知识点拨
函数最大值与最小值
最大值 最小值
条件 设y=f(x)的定义域为A.如果存在x0∈A,使得对于任意的x∈A,都有 f(x)≤f(x0) f(x)≥f(x0)
结论 那么称f(x0)为y=f(x)的最大值,记为ymax=f(x0) 那么称f(x0)为y=f(x)的最小值,记为ymin=f(x0)
几何 意义 f(x)图象上最高点的纵坐标 f(x)图象上最低点的纵坐标
名师点析 函数最大(小)值和值域的联系与区别
(1)联系:函数的最大(小)值和值域反映的都是函数的整体性质,针对的是整个定义域.
(2)区别:①函数的值域一定存在,而函数的最大(小)值不一定存在;②若函数的最大(小)值存在,则最大(小)值一定是值域中的元素,例如:函数f(x)=x2对任意的x∈R,都有f(x)≥-1,但是f(x)的最小值不是-1,因为-1不在f(x)的值域内.
微思考
若函数f(x)≤M,则M一定是函数的最大值吗
提示 不一定,只有定义域内存在一点x0,使f(x0)=M时,M才是函数的最大值,否则不是.
微练习 1
已知函数f(x)在区间[-2,2]上的图象如图所示,则该函数的最小值、最大值分别是( )
A.f(-2),0 B.0,2
C.f(-2),2 D.f(2),2
答案 C
解析 由题图可知,该函数的最小值为f(-2),最大值为f(1)=2.
微练习 2
函数f(x)= ,x∈[1,2],则f(x)的最大值为 ,最小值为 .
探究一
利用函数的图象求函数的最大(小)值
(1)在直角坐标系内画出f(x)的图象;
(2)根据函数的图象写出函数的单调区间、最大值、最小值.
解 (1)f(x)的图象如图所示.
(2)由图可知f(x)的增区间为[-1,0],[2,5],减区间为[0,2],最大值为3,最小值为-1.
反思感悟利用图象求函数最大(小)值的方法
(1)画出函数y=f(x)的图象;
(2)观察图象,找出图象的最高点(最低点);
(3)写出最大(小)值,最高点的纵坐标是函数的最大值(最低点的纵坐标是函数的最小值).
变式训练1函数y=f(x),x∈[-2,2]的图象如图所示,则函数的最大值、最小值分别为( )
答案 C
探究二
利用函数的单调性求最大(小)值
(1)判断函数在区间(-1,+∞)上的单调性,并用定义证明你的结论;
(2)求该函数在区间[2,4]上的最大值和最小值.
解 (1)f(x)在(-1,+∞)上为增函数,证明如下,任取-1因为-10,x2+1>0,x1-x2<0,
所以f(x1)-f(x2)<0,即f(x1)所以f(x)在(-1,+∞)上为增函数.
(2)由(1)知f(x)在[2,4]上为增函数,
反思感悟函数的最大(小)值与单调性的关系
(1)若函数f(x)在区间[a,b]上是增(减)函数,则f(x)在区间[a,b]上的最小(大)值是f(a),最大(小)值是f(b).
(2)若函数f(x)在区间[a,b]上是增(减)函数,在区间[b,c]上是减(增)函数,则f(x)在区间[a,c]上的最大(小)值是f(b),最小(大)值是f(a)与f(c)中较小(大)的一个.
变式训练2求函数f(x)=x+ 在[1,4]上的最大值和最小值.
∵x10,1∴f(x1)>f(x2),即f(x)在区间[1,2]上是减函数.
同理f(x)在[2,4]上是增函数.
∴当x=2时,f(x)取得最小值4;当x=1或x=4时,f(x)取得最大值5.
探究三
二次函数的最大(小)值问题
例3已知函数f(x)=x2-ax+1,求f(x)在[0,1]上的最大值.
综上,当a≤1时,f(x)在[0,1]上的最大值为2-a;当a>1时,f(x)在[0,1]上的最大值为1.
延伸探究在本例条件不变的情况下,求f(x)在[0,1]上的最小值.
综上,当a≤0时,f(x)在[0,1]上的最小值为1;
当0当a≥2时,f(x)在[0,1]上的最小值为2-a.
反思感悟二次函数“轴动区间定”问题的求解策略
“轴动区间定”型的问题,对于对称轴的位置变化情况必须进行分类讨论,其分类标准为对称轴与x轴交点横坐标在给定区间内变化;对称轴与x轴交点横坐标在给定区间外变化.若对称轴与x轴交点横坐标只能在给定区间内变化,则只需考虑其与端点的距离.
变式训练3求函数y=x2-2ax-1在区间[0,2]上的最大值与最小值.
解 y=(x-a)2-1-a2.
当a<0时,函数在[0,2]上是增函数,如图①.
故函数在x=0处取得最小值-1,
在x=2处取得最大值3-4a.
当0≤a≤1时,结合函数图象(如图②)知,
函数在x=a处取得最小值-a2-1,
在x=2处取得最大值3-4a.
当1函数在x=a处取得最小值-a2-1,
在x=0处取得最大值-1.
当a>2时,函数在[0,2]上是减函数,如图④.
函数在x=0处取得最大值-1,在x=2处取得最小值3-4a.
综上,当a<0时,函数在区间[0,2]上的最小值为-1,最大值为3-4a;
当0≤a≤1时,函数在区间[0,2]上的最小值为-a2-1,最大值为3-4a;
当1当a>2时,函数在区间[0,2]上的最小值为3-4a,最大值为-1.
素养形成
函数最大(小)值的实际应用
解决函数应用题的基本思路
典例 一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x(x∈N*)件.当x≤20时,年销售总收入为(33x-x2)万元;当x>20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元.(年利润=年销售总收入-年总投资)
(1)求y与x的函数关系式.
(2)当该工厂的年产量为多少件时,所得年利润最大 最大年利润是多少
解 (1)当0当x>20时,y=260-100-x=160-x.
(2)当0而当x>20时,160-x<140.
故当该工厂年产量为16件时,取得最大年利润,最大年利润为156万元.
点评解实际应用题的四个步骤
(1)审题:解读实际问题,找出已知条件、未知条件,确定自变量和因变量的条件关系.
(2)建模:建立数学模型,列出函数关系式.
(3)求解:分析函数性质,利用数学知识探究问题解法(一定注意自变量的取值范围).
(4)回归:数学问题回归实际问题,写出答案.
当堂检测
A.10,6 B.10,8
C.8,6 D.以上都不对
答案 A
解析 当1≤x≤2时,8≤2x+6≤10,当-1≤x<1时,6≤x+7<8,
∴f(x)min=f(-1)=6,f(x)max=f(2)=10.故选A.
答案 B
3.函数y=x2-2x,x∈[0,3]的值域为( )
A.[0,3] B.[-1,0]
C.[-1,+∞) D.[-1,3]
答案 D
解析 ∵函数y=x2-2x=(x-1)2-1,x∈[0,3],∴当x=1时,函数y取得最小值-1,当x=3时,函数取得最大值3,故函数的值域为[-1,3],故选D.
4.函数f(x)=x2-4x+3,x∈[1,4],则f(x)的最大值为 .
答案 3
解析 由题意,函数f(x)=x2-4x+3=(x-2)2-1,x∈[1,4],所以当x=4时,f(x)取最大值f(4)=3.
5.函数y=ax+1在区间[1,3]上的最大值为4,则a= .
答案 1
解析 若a<0,则函数y=ax+1在区间[1,3]上是减函数,并且在区间的左端点处取得最大值,即a+1=4,解得a=3,不满足a<0,舍去;若a>0,则函数y=ax+1在区间[1,3]上是增函数,并且在区间的右端点处取得最大值,即3a+1=4,解得a=1.综上,a=1.
6.已知函数f(x)= (x∈[2,6]).
(1)判断函数f(x)的单调性,并证明;
(2)求函数的最大值和最小值.
解 (1)函数f(x)在[2,6]上是减函数.
设x1,x2是区间[2,6]上的任意两个实数,且x1由2≤x10,(x1-1)(x2-1)>0,
于是f(x1)-f(x2)>0,即f(x1)>f(x2),
谢谢观看
高中数学苏教版必修第一册
第5章 函数的概念与性质
5.3 函数的单调性
第1课时 函数的单调性
课标阐释 思维脉络
1.理解函数的单调性及其几何意义,能运用函数图象理解和研究函数的单调性.(直观想象)
2.会用函数单调性的定义判断(或证明)一些函数的单调性.(逻辑推理)
3.会求一些具体函数的单调区间.(数学运算)
情境导入
德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:
时间间隔t 刚记忆完毕 20分钟后 60分钟后 8~9小时后 1天后 2天后 6天后 一个月后
记忆量y (百分比) 100 58.2 44.2 35.8 33.7 27.8 25.4 21.1
以上数据表明,记忆量y是时间间隔t的函数,艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯遗忘曲线”,如图.
当时间间隔t逐渐增大时,你能看出对应的函数值y有什么变化趋势吗 通过这个试验,你打算以后如何对待刚学过的知识
知识点拨
一、增函数与减函数
条件 设函数y=f(x)的定义域为A,区间I A. 如果对于区间I内的任意两个值x1,x2,当x1
结论 那么称y=f(x)在区间I上是增函数,I称为y=f(x)的增区间 那么称y=f(x)在区间I上是减函数,I称为y=f(x)的减区间
图示
名师点析 增(减)函数定义中的x1,x2的特征
(1)任意性,即“任意两个值x1,x2”中“任意”二字绝不能去掉,证明时不能以特殊代替一般;
(2)有大小,通常规定x1
这三个条件缺一不可.
微练习 1
下列函数在区间(0,+∞)上是减函数的是( )
A.y=- B.y=x
C.y=x2 D.y=1-x
答案 D
解析 函数y=1-x在区间(0,+∞)上是减函数,其余函数在(0,+∞)上均为增函数,故选D.
微练习 2
已知函数f(x)是定义在R上的增函数,则f(x)=0的根( )
A.有且只有一个 B.有两个
C.至多一个 D.以上均不对
答案 D
解析 因为f(x)在R上是增函数,所以对任意x1,x2∈R,若x1
如果函数y=f(x)在区间I上是增函数或减函数,那么称函数y=f(x)在区间I上具有单调性,增区间和减区间统称为单调区间.
名师点析 1.区间I必为函数定义域A的子集,即I A,所以单调性是函数定义域内的局部性质.
2.函数的单调区间可以是整个定义域,也可以是定义域的真子集.如y=x在整个定义域(-∞,+∞)上是增函数,y=-x在整个定义域(-∞,+∞)上是减函数,但y=x2在定义域(-∞,+∞)上不具有单调性,其在(-∞,0)上是减函数,在(0,+∞)上是增函数.
3.一个函数出现两个或两个以上单调区间时,单调区间用“,”隔开,或者用“和”连接,不能用“并”或“且”连接.
微思考
函数y= 在定义域上是减函数吗
提示 不是.y= 在(-∞,0)上是减函数,在(0,+∞)上也是减函数,但不能说y=在(-∞,0)∪(0,+∞)上是减函数.
微练习
函数y=f(x)的图象如图所示,其减区间是( )
A.[-4,4]
B.[-4,-3]和[1,4]
C.[-3,1]
D.[-3,4]
答案 B
解析 由图可知,函数y=f(x)的减区间为[-4,-3]和[1,4].故选B.
探究一
函数单调性的判断与证明
例1证明函数f(x)=x+ 在(0,1)上是减函数.
证明 设x1,x2是区间(0,1)上的任意两个实数,且x1
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴f(x)=x+ 在(0,1)上是减函数.
反思感悟利用定义证明函数单调性的步骤
(1)取值:设x1,x2是该区间内的任意两个值,且x1
(3)定号:确定f(x1)-f(x2)的符号.
(4)结论:根据f(x1)-f(x2)的符号及定义判断单调性.
变式训练1试用函数单调性的定义证明f(x)= 在(1,+∞)上是减函数.
因为1
所以f(x1)>f(x2),
所以f(x)在(1,+∞)上是减函数.
探究二
求函数的单调区间
例2求下列函数的单调区间,并指出该函数在其单调区间上是增函数还是减函数.
(3)f(x)=-x2+2|x|+3.
解 (1)函数f(x)=- 的单调区间为(-∞,0),(0,+∞),其在(-∞,0),(0,+∞)上都是增函数.
(2)当x≥1时,f(x)是增函数,当x<1时,f(x)是减函数,所以f(x)的单调区间为
(-∞,1),[1,+∞),并且函数f(x)在(-∞,1)上是减函数,在[1,+∞)上是增函数.
根据解析式可作出函数的图象如图所示,由图象可知,函数f(x)的单调区间为(-∞,-1],[-1,0],[0,1],[1,+∞).
f(x)在(-∞,-1],[0,1]上是增函数,在[-1,0],[1,+∞)上是减函数.
反思感悟1.求函数单调区间的方法
(1)利用基本初等函数的单调性,如本例(1)和(2),其中分段函数的单调区间要根据函数的自变量的取值范围分段求解;
(2)利用函数的图象,如本例(3).
2.若所求出函数的增区间或减区间不唯一,函数的单调区间之间要用“,”或“和”连接,如本例(3).
变式训练2(1)根据图象说出函数在每一单调区间上,是增函数还是减函数;
(2)写出y=|x2-2x-3|的单调区间.
解 (1)函数在[-1,0],[2,4]上是减函数,在[0,2],[4,5]上是增函数.
(2)先画出
则y=|x2-2x-3|的减区间为(-∞,-1],[1,3];增区间为[-1,1],[3,+∞).
探究三
函数单调性的综合应用
例3已知函数f(x)=x2+ax+b.
(1)若函数f(x)的图象过点(1,4)和(2,5),求f(x)的解析式;
(2)若函数f(x)在区间[1,2]上不具有单调性,求实数a的取值范围.
解 (1)∵f(x)=x2+ax+b过点(1,4)和(2,5),
(2)由f(x)在区间[1,2]上不具有单调性可知1<- <2,即-4
延伸探究把本例(2)条件“不具有单调性”改为“具有单调性”,求实数a的取值范围.
反思感悟函数单调性的应用
(1)函数单调性定义的“双向性”:利用定义可以判断、证明函数的单调性,反过来,若已知函数的单调性可以确定函数中参数的取值范围.
(2)若一个函数在区间[a,b]上具有单调性,则此函数在这一单调区间内的任意子集上也具有单调性.
变式训练3已知函数g(x)在(-∞,+∞)上是增函数,且g(2x-3)>g(5x+6),求实数x的取值范围.
解 ∵g(x)在(-∞,+∞)上是增函数,且g(2x-3)>g(5x+6),
∴2x-3>5x+6,即x<-3.
故实数x的取值范围为(-∞,-3).
素养形成
抽象函数的单调性
抽象函数是指没有给出具体解析式的函数.
判断抽象函数单调性的方法:
1.凑:凑定义或凑已知,利用定义或已知条件得出结论;
2.赋值:给变量赋值要根据条件与结论的关系,有时可能要进行多次尝试.
典例 已知定义在(0,+∞)上的函数f(x)对任意x,y∈(0,+∞),恒有f(xy)=f(x)+f(y),且当0
解 f(x)在(0,+∞)上是减函数.
理由如下,设x1,x2是区间(0,+∞)上的任意两个值,且x1
即f(x1)>f(x2).
∴函数f(x)在(0,+∞)上是减函数.
点评一般地,若给出的抽象函数的性质为“f(x+y)=…”,则称这类抽象函数为“和型抽象函数”,研究“和型抽象函数”的单调性的基本方法是将x拆成两个数的和“(x-y)+y”,利用所给的性质及条件,即可确定其单调性;类似地,“积型抽象函数”(即“f(xy)=…”)只需将x拆成两个数的积“x=y· (y≠0)”即可.
当堂检测
1.如图是定义在区间[-5,5]上的函数y=f(x),则下列关于函数f(x)的说法错误的是( )
A.函数在区间[-5,-3]上是增函数
B.函数在区间[1,4]上是增函数
C.函数在区间[-3,1]∪[4,5]上是减函数
D.函数在区间[-5,5]上没有单调性
答案 C
解析 由图可知,f(x)在区间[-3,1],[4,5]上是减函数,单调区间不可以用并集“∪”连接,故选C.
2.函数f(x)在R上是减函数,则有( )
A.f(3)
答案 C
解析 ∵3<5,且f(x)在R上是减函数,∴f(3)>f(5).
3.(2020北京北理工附中期中)下列函数在区间(0,+∞)上为增函数的是( )
答案 B
对于C,函数y=(x-1)2+1在(0,1)上是减函数,在(1,+∞)上是增函数,故C错误;
对于D,函数y=-x2在(0,+∞)上是减函数,故D错误.
故选B.
4.(2020浙江宁波高二期中)已知函数f(x)在R上是减函数,且f(2)=-1,则满足f(2x-4)>-1的实数x的取值范围是 .
答案 (-∞,3)
解析 由f(2)=-1知,若满足f(2x-4)>-1,
则f(2x-4)>f(2).
又函数f(x)在R上是减函数,则2x-4<2,解得x<3,
所以实数x的取值范围为(-∞,3).
5.已知函数f(x)= (k≠0)在区间(0,+∞)上是增函数,则实数k的取值范围是 .
答案 (-∞,0)
解析 结合反比例函数的单调性可知k<0.
高中数学苏教版必修第一册
第5章 函数的概念与性质
5.3 函数的单调性
第2课时 函数的最大(小)值
课标阐释 思维脉络
1.理解函数的最大值和最小值的概念及其几何意义.(数学抽象)
2.能借助函数的图象和单调性,求一些简单函数的最值.(直观想象)
3.能利用函数的最值解决有关的实际应用问题.(数学建模)
情境导入
请同学们认真观察一次函数f(x)=x和二次函数f(x)=x2的图象,在它们的图象上是否存在最高点或最低点 显然,一次函数f(x)=x的图象上不存在最高点,也不存在最低点.二次函数f(x)=x2的图象上不存在最高点,但存在最低点(0,0),即坐标原点.即当一个函数f(x)的图象有最低点时,我们就说函数f(x)有最小值;而一次函数f(x)=x的图象没有最低点,所以函数f(x)=x没有最小值.
你能用数学语言描述函数最小值的定义吗
知识点拨
函数最大值与最小值
最大值 最小值
条件 设y=f(x)的定义域为A.如果存在x0∈A,使得对于任意的x∈A,都有 f(x)≤f(x0) f(x)≥f(x0)
结论 那么称f(x0)为y=f(x)的最大值,记为ymax=f(x0) 那么称f(x0)为y=f(x)的最小值,记为ymin=f(x0)
几何 意义 f(x)图象上最高点的纵坐标 f(x)图象上最低点的纵坐标
名师点析 函数最大(小)值和值域的联系与区别
(1)联系:函数的最大(小)值和值域反映的都是函数的整体性质,针对的是整个定义域.
(2)区别:①函数的值域一定存在,而函数的最大(小)值不一定存在;②若函数的最大(小)值存在,则最大(小)值一定是值域中的元素,例如:函数f(x)=x2对任意的x∈R,都有f(x)≥-1,但是f(x)的最小值不是-1,因为-1不在f(x)的值域内.
微思考
若函数f(x)≤M,则M一定是函数的最大值吗
提示 不一定,只有定义域内存在一点x0,使f(x0)=M时,M才是函数的最大值,否则不是.
微练习 1
已知函数f(x)在区间[-2,2]上的图象如图所示,则该函数的最小值、最大值分别是( )
A.f(-2),0 B.0,2
C.f(-2),2 D.f(2),2
答案 C
解析 由题图可知,该函数的最小值为f(-2),最大值为f(1)=2.
微练习 2
函数f(x)= ,x∈[1,2],则f(x)的最大值为 ,最小值为 .
探究一
利用函数的图象求函数的最大(小)值
(1)在直角坐标系内画出f(x)的图象;
(2)根据函数的图象写出函数的单调区间、最大值、最小值.
解 (1)f(x)的图象如图所示.
(2)由图可知f(x)的增区间为[-1,0],[2,5],减区间为[0,2],最大值为3,最小值为-1.
反思感悟利用图象求函数最大(小)值的方法
(1)画出函数y=f(x)的图象;
(2)观察图象,找出图象的最高点(最低点);
(3)写出最大(小)值,最高点的纵坐标是函数的最大值(最低点的纵坐标是函数的最小值).
变式训练1函数y=f(x),x∈[-2,2]的图象如图所示,则函数的最大值、最小值分别为( )
答案 C
探究二
利用函数的单调性求最大(小)值
(1)判断函数在区间(-1,+∞)上的单调性,并用定义证明你的结论;
(2)求该函数在区间[2,4]上的最大值和最小值.
解 (1)f(x)在(-1,+∞)上为增函数,证明如下,任取-1
所以f(x1)-f(x2)<0,即f(x1)
(2)由(1)知f(x)在[2,4]上为增函数,
反思感悟函数的最大(小)值与单调性的关系
(1)若函数f(x)在区间[a,b]上是增(减)函数,则f(x)在区间[a,b]上的最小(大)值是f(a),最大(小)值是f(b).
(2)若函数f(x)在区间[a,b]上是增(减)函数,在区间[b,c]上是减(增)函数,则f(x)在区间[a,c]上的最大(小)值是f(b),最小(大)值是f(a)与f(c)中较小(大)的一个.
变式训练2求函数f(x)=x+ 在[1,4]上的最大值和最小值.
∵x1
同理f(x)在[2,4]上是增函数.
∴当x=2时,f(x)取得最小值4;当x=1或x=4时,f(x)取得最大值5.
探究三
二次函数的最大(小)值问题
例3已知函数f(x)=x2-ax+1,求f(x)在[0,1]上的最大值.
综上,当a≤1时,f(x)在[0,1]上的最大值为2-a;当a>1时,f(x)在[0,1]上的最大值为1.
延伸探究在本例条件不变的情况下,求f(x)在[0,1]上的最小值.
综上,当a≤0时,f(x)在[0,1]上的最小值为1;
当0
反思感悟二次函数“轴动区间定”问题的求解策略
“轴动区间定”型的问题,对于对称轴的位置变化情况必须进行分类讨论,其分类标准为对称轴与x轴交点横坐标在给定区间内变化;对称轴与x轴交点横坐标在给定区间外变化.若对称轴与x轴交点横坐标只能在给定区间内变化,则只需考虑其与端点的距离.
变式训练3求函数y=x2-2ax-1在区间[0,2]上的最大值与最小值.
解 y=(x-a)2-1-a2.
当a<0时,函数在[0,2]上是增函数,如图①.
故函数在x=0处取得最小值-1,
在x=2处取得最大值3-4a.
当0≤a≤1时,结合函数图象(如图②)知,
函数在x=a处取得最小值-a2-1,
在x=2处取得最大值3-4a.
当1
在x=0处取得最大值-1.
当a>2时,函数在[0,2]上是减函数,如图④.
函数在x=0处取得最大值-1,在x=2处取得最小值3-4a.
综上,当a<0时,函数在区间[0,2]上的最小值为-1,最大值为3-4a;
当0≤a≤1时,函数在区间[0,2]上的最小值为-a2-1,最大值为3-4a;
当1
素养形成
函数最大(小)值的实际应用
解决函数应用题的基本思路
典例 一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x(x∈N*)件.当x≤20时,年销售总收入为(33x-x2)万元;当x>20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元.(年利润=年销售总收入-年总投资)
(1)求y与x的函数关系式.
(2)当该工厂的年产量为多少件时,所得年利润最大 最大年利润是多少
解 (1)当0
(2)当0
故当该工厂年产量为16件时,取得最大年利润,最大年利润为156万元.
点评解实际应用题的四个步骤
(1)审题:解读实际问题,找出已知条件、未知条件,确定自变量和因变量的条件关系.
(2)建模:建立数学模型,列出函数关系式.
(3)求解:分析函数性质,利用数学知识探究问题解法(一定注意自变量的取值范围).
(4)回归:数学问题回归实际问题,写出答案.
当堂检测
A.10,6 B.10,8
C.8,6 D.以上都不对
答案 A
解析 当1≤x≤2时,8≤2x+6≤10,当-1≤x<1时,6≤x+7<8,
∴f(x)min=f(-1)=6,f(x)max=f(2)=10.故选A.
答案 B
3.函数y=x2-2x,x∈[0,3]的值域为( )
A.[0,3] B.[-1,0]
C.[-1,+∞) D.[-1,3]
答案 D
解析 ∵函数y=x2-2x=(x-1)2-1,x∈[0,3],∴当x=1时,函数y取得最小值-1,当x=3时,函数取得最大值3,故函数的值域为[-1,3],故选D.
4.函数f(x)=x2-4x+3,x∈[1,4],则f(x)的最大值为 .
答案 3
解析 由题意,函数f(x)=x2-4x+3=(x-2)2-1,x∈[1,4],所以当x=4时,f(x)取最大值f(4)=3.
5.函数y=ax+1在区间[1,3]上的最大值为4,则a= .
答案 1
解析 若a<0,则函数y=ax+1在区间[1,3]上是减函数,并且在区间的左端点处取得最大值,即a+1=4,解得a=3,不满足a<0,舍去;若a>0,则函数y=ax+1在区间[1,3]上是增函数,并且在区间的右端点处取得最大值,即3a+1=4,解得a=1.综上,a=1.
6.已知函数f(x)= (x∈[2,6]).
(1)判断函数f(x)的单调性,并证明;
(2)求函数的最大值和最小值.
解 (1)函数f(x)在[2,6]上是减函数.
设x1,x2是区间[2,6]上的任意两个实数,且x1
于是f(x1)-f(x2)>0,即f(x1)>f(x2),
谢谢观看
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
